| Раздел функций | ИНЖЕНЕРНЫЕ |
| Название на английском | DELTA |
| Волатильность | Не волатильная |
| Похожие функции | СОВПАД, ВПР |
Что делает эта функция?
Эта функция сравнивает два значения и проверяет, являются ли они абсолютно одинаковыми.
Если числа совпадают, результатом будет 1, в противном случае – 0.
Работает только с числами, текстовые значения на входе отдают результат #ЗНАЧ!
Форматирование числа не имеет существенного значения, поэтому числа, которые выглядят округленными из-за удаления десятичных разрядов, будут по-прежнему корректно соответствовать не округленным значениям.
Синтаксис
=ДЕЛЬТА(ПервоеЧисло;ВтороеЧисло)
Пример
Следующая таблица используется для определения того, сколько одинаковых пар чисел в списке.
Функция ДЕЛЬТА проверяет каждую пару, а затем функция СУММ суммирует их.
По иронии судьбы, функция ДЕЛЬТА не поможет посчитать дельту в Excel. Сравнивая данные в ячейках, функция лишь отвечает на вопрос, равна ли их дельта нулю или нет (иными словами, есть ли дельта).
А посчитать дельту между A и B можно без применения каких-либо функций вовсе, лишь зная две простые формулы ее подсчета:
Второй вариант в Excel использовать удобнее, т.к. первый требует использования скобок.
Не дайте буквам в формуле вас запутать – B обозначает первый замер (результат “до”), а A – второй (результат “после”). Иными словами, A случилось после B, их алфавитный порядок здесь не при чем.
Чтобы полученный результат выражался в процентах, нужно изменить формат ячеек на процентный:
Другие инженерные функции
ДВ.В.ДЕС, ДЕС.В.ДВ, ДЕС.В.ШЕСТН, ПОРОГ, ПРЕОБР, ШЕСТН.В.ДЕС
Функция ДЕЛЬТА в Excel используется для проверки двух числовых значений и возвращает два возможных варианта:
- Числовое значение 1, если переданные в качестве первого и второго аргумента числа совпадают по значению.
- 0 (нуль), если переданные числа по значению не совпадают.
Примеры использования функции ДЕЛЬТА в Excel
Пример 1. В таблице Excel указаны значения независимой координаты X и значения зависимых координат Y1 и Y2 для двух разных функций. Определить количество пар совпадающих значений.
Вид исходной таблицы данных:
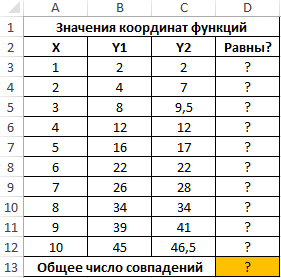
Для решения задачи сравним каждую пару значений зависимых координат Y1 и Y2 с помощью функции ДЕЛЬТА. В ячейке D3 запишем следующую формулу:
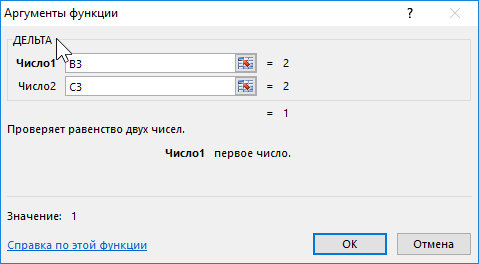
Описание аргументов:
- B3 – значение аргумента Y1 – сравниваемое число;
- C3 – значение аргумента Y2 – число, с которым сравнивается первое значение.
Полученное значение (1) свидетельствует о равенстве сравниваемых чисел. Протянем записанную в ячейке D3 формулу вниз до ячейки D12, чтобы автоматически рассчитать результаты для остальных значений Y1 и Y2:
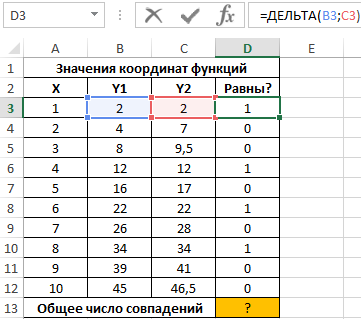
Для расчета числа пар совпадающих значений используем следующую функцию:
=СУММ(D3:D12)
Полученный результат:
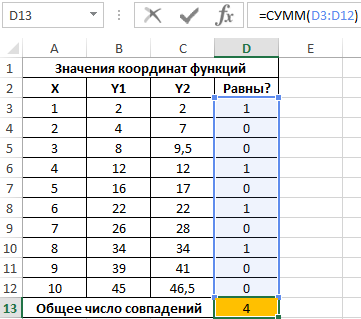
Всего 4 пары совпадений в значениях функций координат.
Калькулятор сроков возврата инвестиций в банковские депозиты
Пример 2. Реализовать калькулятор, который рассчитывает, сколько времени потребуется на получение определенной прибыли от депозита при известной начальной сумме вклада и годовой процентной ставки. Предусмотреть вывод сообщения об ошибке в случае, если одно или несколько исходных данных не указаны.
Вид формы для расчета:
Поскольку для расчета используется логарифм из частного ожидаемой и начальной суммы с основанием в виде суммы депозита, выраженного в процентах (то есть 100%), и процентной ставки, то каждая ячейка из диапазона B2:B4 не должна являться пустой или принимать значение 0, поскольку логарифм нуля или логарифм с основанием 1 (100%) не может быть вычислен. Поэтому для расчетов используем следующую формулу:
В качестве проверочного выражения функции ЕСЛИ выступает значение, являющееся суммой возвращаемых результатов функциями ДЕЛЬТА. Последние сравнивают значения, содержащиеся в ячейках B2, B3 и B4 соответственно с 0 (второй аргумент явно не указан). Данный вариант записи соответствует логическому И (общий результат равен ИСТИНА, если все выражения, проверяемые функцией И, возвращают результат ИСТИНА). Полученное значение (0 или любое число от 1 до +∞) будет интерпретировано как ЛОЖЬ или ИСТИНА соответственно.
При незаполненных полях получим следующий результат:
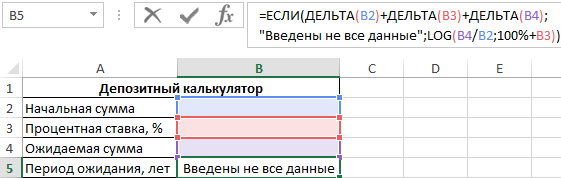
Пример расчета:
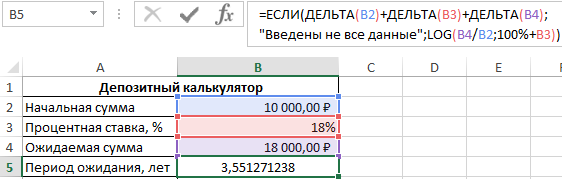
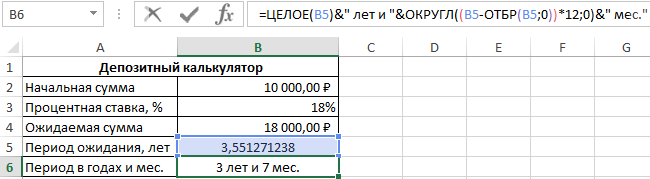
Напишем формулу для преобразования дробного числа в годы и месяцы:
В результате получим:
Расчет вероятности выпуска бракованной продукции на производстве в Excel
Пример 3. При изготовлении деталей на производственно-ремонтном заводе существует вероятность брака производимой продукции, которая равная коэффициенту 0,001. Определить, какая вероятность появления 10 выбракованных деталей (в этом случае вся партия считается браком) в партии из 35000 шт. Считается, что вероятностями ниже 10% можно пренебречь (то есть их приравнивают к нулю).
Вид исходной таблицы данных:
Для расчета используем следующую формулу:
Функция ОКРУГЛВНИЗ округляет до 0 все значения, которые меньше числа 0,01, то есть 10%-й вероятности. Функция ДЕЛЬТА принимает только один аргумент (выражение, полученное на основе формулы Пуассона для вычисления маловероятных случайных ситуаций), то есть сравнение выполняется с числом 0 (нуль).
Результат вычислений:
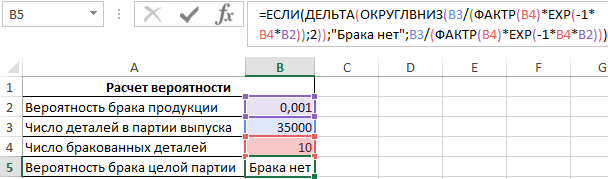
Если вычислять формулу поэтапно, будет видно, что вероятность по формуле Пуассона равна примерно 0,00974 < 0,01, поэтому результат округления равен 0. Тогда функция ДЕЛЬТА возвращает значение 1 (0=0), которое интерпретируется как логическое ИСТИНА.
Особенности использования функции ДЕЛЬТА в Excel
Функция имеет следующий синтаксис:
=ДЕЛЬТА(число1;[число2])
Описание аргументов:
- число1 – обязательный аргумент, принимающий данные числового типа, которые будут сравнены по значению с числом, переданным в качестве второго аргумента, или нулем, если последний опущен;
- [число2] – необязательный для заполнения аргумент, характеризующий числовое значение, с которым выполняется операция сравнения. Если явно не указан, принимает значение 0 (нуль).
Примечания:
- Рассматриваемая функция выполняет операцию сравнения только числовых значений. Если в качестве одного из аргументов было передано имя, текстовая строка или логические ИСТИНА и ЛОЖЬ, результатом выполнения функции ДЕЛЬТА будет код ошибки #ЗНАЧ!.
- Функция ДЕЛЬТА может быть использована для сравнения двух дат, которые являются результатами выполнения функции ДАТА или других функций, возвращающих данные формата Дата, поскольку Excel выполняет автоматическое преобразование в формат времени Excel (соответствующее числовое значение).
- Если в качестве первого аргумента функции ДЕЛЬТА было передано число 0, а в качестве второго – ссылка на пустую ячейку, результатом вычислений будет число 1, поскольку пустое значение интерпретируется как числовое значение 0.
- Рассматриваемая функция также имеет название дельта-функция Кронекера.
- Данную функцию можно использовать вместо логического знака равенства «=» в выражениях, которые используются как условия проверки в логических функциях. Например, функция =ЕСЛИ(ДЕЛЬТА(1;1);”равны”;”не равны”) вернет значение «равны». При этом преобразование чисел 1 и 0 в логические ИСТИНА и ЛОЖЬ выполняется автоматически.
- Функция ДЕЛЬТА не может быть использована в качестве формулы массива. Например, формула массива =ДЕЛЬТА (A1:A5;B1B5) вернет массив ошибок #ЗНАЧ!, даже если ячейки из диапазонов A1:A5 и B1:B5 содержат только числовые значения.
Разница в процентах между двумя числами в Excel
Познакомимся с особенностями расчета разницы между двумя числами в процентах в Excel в зависимости от знаков рассматриваемых величин (обе величины положительные, обе отрицательные или разных знаков).
Приветствую всех, уважаемые читатели блога TutorExcel.Ru.
Кажется, что может быть проще, чем посчитать дельту в процентах между двумя числами — это несложная математическая операция.
Сначала вычислить разницу между двумя величинами в абсолютном выражении (разность первого и второго чисел), а затем полученный результат разделить на вторую величину.
Но все несколько сложнее, чем кажется на первый взгляд, и для некоторых случаев приведенная формула может дать неправильный результат. Поэтому давайте перейдем к рассмотрению особенностей вычислений.
Формула разницы между числами в процентах в Excel
Для удобства записи обозначим первую величину как A, а вторую как B.
Тогда процентный прирост первого числа ко второму, как уже писалось выше, будет считаться по следующей формуле:
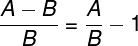
Теперь перейдем к проверке корректности формулы расчета и рассмотрим различные примеры в зависимости от знаков величин A и B.
Вариант 1: A и B одного знака (+ и +, или − и −)
Начнем со стандартного варианта, когда мы сравниваем друг с другом сопоставимые величины.
Предположим, что компания в этом году продала товаров на сумму 120 тысяч рублей, а в прошлом году — на сумму 100 тысяч рублей.
Вычислим темпы роста доходов компании год к году, т.е. посмотрим насколько компания в этом году заработала в процентах больше, чем в прошлом.
В данном случае, A это 120 тысяч рублей, а B, соответственно, 100 тысяч рублей, применим формулу и найдем соотношение между ними:
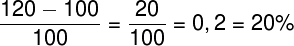
В итоге получаем, что 120 тысяч рублей больше, чем 100 тысяч рублей на 20%.
Действительно, все достаточно просто, но теперь рассмотрим те же самые величины, но с обратным знаком: -120 и -100.
И для лучшей наглядности расчета рассмотрим не доходы компании, а ее убытки, и представим, что убытки компании в этом году составили -120 тысяч рублей, когда в прошлом году составляли -100 тысяч рублей.
Логично предположить, что мы должны получить ответ -20%, так как на самом деле -120 меньше, чем -100 (с точки зрения математики, чем левее число на числовой оси, тем оно меньше) и, следовательно, в результате получить отрицательный процентный прирост.
Другими словами, убытки компании увеличились и результаты компании ухудшились, а значит прирост в процентах отрицательный.
Проверяем формулу и повторяем расчет:
Однако мы опять получаем результат 20%, который, как мы уже выяснили, является неправильным.
Поэтому отсюда делаем вывод, что наша формула для отрицательных чисел, к сожалению, не работает.
Скорректируем расчет, вместо величины B в знаменателе формулы поставим ее модуль.
Тогда формула расчета разницы в процентах примет окончательный вид:
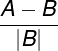
Пересчитаем пример и посмотрим какой ответ в итоге получится:
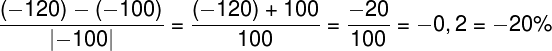
Отлично, все сошлось. При этом обратите внимание, что для положительных величин формула на самом деле осталась прежней и никак не поменялась, так как модуль положительные числа не изменяет.
Идем дальше и рассмотрим более сложный вариант.
Вариант 2: A и B разных знаков (+ и −, или − и +)
Теперь разберем нестандартный вариант, и от сравнения чисел одинаковых знаков (до этого мы сравнивали положительное с положительным и отрицательное с отрицательным) перейдем к сравнению чисел разных знаков.
Однако при попытке произвести такое сравнение, мы приходим к логическому несоответствию.
Например, давайте подумаем во сколько число 20 больше числа -5?
Предположим, что мы каким-то образом посчитали отношение и нашли численный ответ (предположу, что на предыдущий вопрос в качестве ответа хочется сказать, что в 5 раз больше):
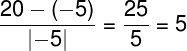
Однако точно такие же расчеты можно привести для чисел 20 и 4 (получается, что 20 одновременно в 5 раз больше, и чем 4 и чем -5).
Такого быть не может, в связи с чем получается, что посчитать разницу между двумя величинами с разными знаками в процентах корректно нельзя, так как сравниваются не сопоставимые друг с другом величины.
Поэтому в подобных случаях принято писать N/M — Not Meaningful (также встречаются обозначения N.M., NM), что можно перевести как не имеет смысла или не имеет значения.
В официальных пресс-релизах или презентациях крупных компаний это может обозначаться следующим образом (к примеру, результаты компании Thomson Reuters за 1 квартал 2017 г.):
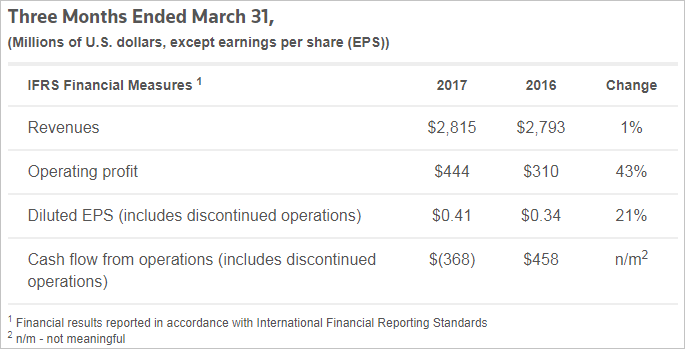
В результате, после всех рассуждений, мы можем вернуться в Excel и составить итоговую формулу расчета разницы в процентах между двумя числами.
Сначала с помощью функции ЕСЛИ проверим условие, что величины одного знака — это равносильно условию, что их произведение больше нуля. В том случае если условие выполняется, то считаем по формуле, если же не выполняется, то в качестве ответа возвращаем ошибку (обозначение NM):
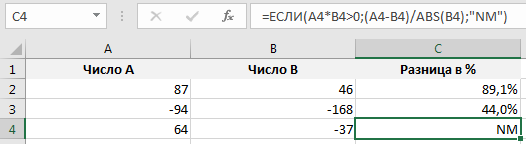
Спасибо за внимание!
Если у вас остались вопросы по методике расчета — спрашивайте в комментариях.
Примеры работы функции ДЕЛЬТА для сравнения двух чисел в Excel
Функция ДЕЛЬТА в Excel используется для проверки двух числовых значений и возвращает два возможных варианта:
- Числовое значение 1, если переданные в качестве первого и второго аргумента числа совпадают по значению.
- 0 (нуль), если переданные числа по значению не совпадают.
Примеры использования функции ДЕЛЬТА в Excel
Пример 1. В таблице Excel указаны значения независимой координаты X и значения зависимых координат Y1 и Y2 для двух разных функций. Определить количество пар совпадающих значений.
Вид исходной таблицы данных:
Для решения задачи сравним каждую пару значений зависимых координат Y1 и Y2 с помощью функции ДЕЛЬТА. В ячейке D3 запишем следующую формулу:
- B3 – значение аргумента Y1 – сравниваемое число;
- C3 – значение аргумента Y2 – число, с которым сравнивается первое значение.
Полученное значение (1) свидетельствует о равенстве сравниваемых чисел. Протянем записанную в ячейке D3 формулу вниз до ячейки D12, чтобы автоматически рассчитать результаты для остальных значений Y1 и Y2:
Для расчета числа пар совпадающих значений используем следующую функцию:
Всего 4 пары совпадений в значениях функций координат.
Калькулятор сроков возврата инвестиций в банковские депозиты
Пример 2. Реализовать калькулятор, который рассчитывает, сколько времени потребуется на получение определенной прибыли от депозита при известной начальной сумме вклада и годовой процентной ставки. Предусмотреть вывод сообщения об ошибке в случае, если одно или несколько исходных данных не указаны.
Вид формы для расчета:
Поскольку для расчета используется логарифм из частного ожидаемой и начальной суммы с основанием в виде суммы депозита, выраженного в процентах (то есть 100%), и процентной ставки, то каждая ячейка из диапазона B2:B4 не должна являться пустой или принимать значение 0, поскольку логарифм нуля или логарифм с основанием 1 (100%) не может быть вычислен. Поэтому для расчетов используем следующую формулу:
В качестве проверочного выражения функции ЕСЛИ выступает значение, являющееся суммой возвращаемых результатов функциями ДЕЛЬТА. Последние сравнивают значения, содержащиеся в ячейках B2, B3 и B4 соответственно с 0 (второй аргумент явно не указан). Данный вариант записи соответствует логическому И (общий результат равен ИСТИНА, если все выражения, проверяемые функцией И, возвращают результат ИСТИНА). Полученное значение (0 или любое число от 1 до +∞) будет интерпретировано как ЛОЖЬ или ИСТИНА соответственно.
При незаполненных полях получим следующий результат:
Напишем формулу для преобразования дробного числа в годы и месяцы:
В результате получим:
Расчет вероятности выпуска бракованной продукции на производстве в Excel
Пример 3. При изготовлении деталей на производственно-ремонтном заводе существует вероятность брака производимой продукции, которая равная коэффициенту 0,001. Определить, какая вероятность появления 10 выбракованных деталей (в этом случае вся партия считается браком) в партии из 35000 шт. Считается, что вероятностями ниже 10% можно пренебречь (то есть их приравнивают к нулю).
Вид исходной таблицы данных:
Для расчета используем следующую формулу:
Функция ОКРУГЛВНИЗ округляет до 0 все значения, которые меньше числа 0,01, то есть 10%-й вероятности. Функция ДЕЛЬТА принимает только один аргумент (выражение, полученное на основе формулы Пуассона для вычисления маловероятных случайных ситуаций), то есть сравнение выполняется с числом 0 (нуль).
Если вычислять формулу поэтапно, будет видно, что вероятность по формуле Пуассона равна примерно 0,00974 число1 ;[число2])
- число1 – обязательный аргумент, принимающий данные числового типа, которые будут сравнены по значению с числом, переданным в качестве второго аргумента, или нулем, если последний опущен;
- [число2] – необязательный для заполнения аргумент, характеризующий числовое значение, с которым выполняется операция сравнения. Если явно не указан, принимает значение 0 (нуль).
- Рассматриваемая функция выполняет операцию сравнения только числовых значений. Если в качестве одного из аргументов было передано имя, текстовая строка или логические ИСТИНА и ЛОЖЬ, результатом выполнения функции ДЕЛЬТА будет код ошибки #ЗНАЧ!.
- Функция ДЕЛЬТА может быть использована для сравнения двух дат, которые являются результатами выполнения функции ДАТА или других функций, возвращающих данные формата Дата, поскольку Excel выполняет автоматическое преобразование в формат времени Excel (соответствующее числовое значение).
- Если в качестве первого аргумента функции ДЕЛЬТА было передано число 0, а в качестве второго – ссылка на пустую ячейку, результатом вычислений будет число 1, поскольку пустое значение интерпретируется как числовое значение 0.
- Рассматриваемая функция также имеет название дельта-функция Кронекера.
- Данную функцию можно использовать вместо логического знака равенства «=» в выражениях, которые используются как условия проверки в логических функциях. Например, функция =ЕСЛИ(ДЕЛЬТА(1;1);”равны”;”не равны”) вернет значение «равны». При этом преобразование чисел 1 и 0 в логические ИСТИНА и ЛОЖЬ выполняется автоматически.
- Функция ДЕЛЬТА не может быть использована в качестве формулы массива. Например, формула массива =ДЕЛЬТА (A1:A5;B1B5) вернет массив ошибок #ЗНАЧ!, даже если ячейки из диапазонов A1:A5 и B1:B5 содержат только числовые значения.
Финансы в Excel+VBA. Калькулятор опционов по модели Блэка-Шоулза
Основы опционов
Для начала кратко о сути и ценообразовании опционов. Опцион имеет четыре основных параметра:
1. Базовый актив
2. Тип опциона (Колл или Пут)
3. Цена страйка (цена исполнения опциона)
4. Дата экспирации (истечения) опциона
Для покупателя опциона он представляет собой право купить (опцион Колл) или продать (опцион Пут) базовый актив по цене страйка в день экспирации. Для продавца опциона он представляет собой обязанность продать (опцион Колл) или купить (опцион Пут) базовый актив по цене страйка в день экспирации. Фактически опцион представляет собой страховку от изменения цены базового актива (БА) от момента сделки до даты экспирации — в роли страховщика выступает продавец (в случае неблагоприятного изменения цены БА он выплачивает страховку покупателю опциона), а страхователем является покупатель опциона (он платит за страховку продавцу).
Как и цена страховки цена опциона полностью определяется вероятностью «страхового случая», т.е. исполнения опциона (исполнения права покупателя опциона). Основные составляющие, которые влияют эту вероятность и на цену опциона, на стоимость страховки, которую платит покупатель и получает продавец:
- Разница между ценой страйка и ценой базового актива. Т.е. при покупке Колла, чем выше его страйк, тем он дешевле (т.к. снижается вероятность того, что на момент экспирации БА будет выше цены страйка)
- Волатильность базового актива. Чем выше волатильность (грубо размах колебаний цены) БА, тем выше вероятность достичь страйка до экспирации.
- Время до экспирации. Чем больше времени до экспирации опциона, тем при покупке Колла выше вероятность что за это время цена базового актива уйдёт выше страйка, соответственно цена опциона выше.
При этом зависимость цены опциона по каждой из этих трёх составляющих нелинейная. Ставшая общепринятой формула оценки опционов с учётом этих основных факторов была выведена Фишером Блэком и Майроном Шоулзом в 1973 году.
Формула Блэка-Шоулза имеет следующий вид (подробно можно посмотреть в Википедии):
Цена (европейского) опциона call: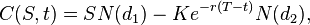 
Цена (европейского) опциона put: 
Обозначения:
C(S,t) — текущая стоимость опциона call в момент t до истечения срока опциона (до экспирации);
S — текущая цена базового актива;
N(x) — вероятность того, что отклонение будет меньше в условиях стандартного нормального распределения (таким образом, и ограничивают область значений для функции стандартного нормального распределения);
K — цена исполнения опциона;
r — безрисковая процентная ставка;
T — t — время до истечения срока опциона;
— волатильность доходности (квадратный корень из дисперсии) базового актива.
Греки опционов
Для оценки чувствительности цены опциона к цене БА, волатильности, и времени до экспирации, применяют коэффициенты, называемые Греками (коэффициенты в основном обозначаются греческими буквами, за исключением «веги»).
Греки в модели Блэка-Шоулза вычисляются следующим образом:
1. Дельта (
) — скорость изменения цены опциона от изменения цены БА. Для опциона Колл дельта равна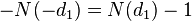 
, для опциона Пут 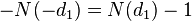. Дельта показывает текущий наклон кривой стоимости опциона в зависимости от цены БА.
2. Гамма (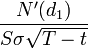 
) — скорость изменения цены опциона от изменения Дельты (или ускорение от изменения цены БА). Гамма равна .
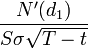3. Вега ( 
) — описывает зависимость цены опциона от изменения волатильности БА: . Вега отражает число пунктов изменения стоимости опциона на каждый процентный пункт (1%) изменения волатильности.
4. Тета (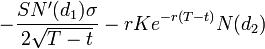 
) — описывает снижение цены опциона в зависимости от времени до экспирации. Для Колла — 
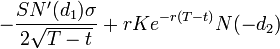, для Пута — .
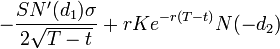Вышеприведенные формулы верны для общего случая, в том числе для случая опционов на акции. Для расчёта опционов на фьючерсные контракты безрисковая ставка r не применяется. Т.к. на Московской бирже торгуются опционы на фьючерсы, далее в расчётах процентную ставку не учитываем.
Реализация модели в MS Excel
Итак, реализация модели Блэка-Шоулза в Excel+VBA.
Для удобства создадим функцию для каждой переменной из модели БШ. В каждой функции будут входные переменные:
S — цена БА
X — цена страйка
d — число дней до экспирации
y — число дней в году
v — волатильность
OptionType — тип опциона «Call» или «Put» (только для расчета цены и дельты)
Запись обычной функции в VBA выглядит следующим образом:
Function НазваниеФункции(входные переменные через запятую)
… вычисления…
НазваниеФункции =… вычисления…
End Function
Такую функцию можно вызывать как из других функций, так и из листа Excel.
Функции записываются в созданный Модуль (запускаем VBA в Excel, например нажатием Alt+F11, выбираем Insert -> Module):
T = d / y
d_1 = (Log(S / X) + (0.5 * (v ^ 2)) * T) / (v * (T ^ 0.5))
End Function
Function d_2(S, X, d, y, v)
T = d / y
d_2 = d_1(S, X, d, y, v) — v * (T ^ 0.5)
End Function
Function Nd_1(S, X, d, y, v)
Nd_1 = Application.NormSDist(d_1(S, X, d, y, v))
End Function
Function Nd_2(S, X, d, y, v)
Nd_2 = Application.NormSDist(d_2(S, X, d, y, v))
End Function
Function N_d_1(S, X, d, y, v)
N_d_1 = Application.NormSDist(-d_1(S, X, d, y, v))
End Function
Function N_d_2(S, X, d, y, v)
N_d_2 = Application.NormSDist(-d_2(S, X, d, y, v))
End Function
Function N1d_1(S, X, d, y, v)
T = d / y
N1d_1 = 1 / (2 * Application.Pi()) ^ 0.5 * (Exp(-0.5 * d_1(S, X, d, y, v) ^ 2))
End Function
Function OptionPrice(OptionType, S, X, d, y, v)
If OptionType = «Call» Then
OptionPrice = S * Nd_1(S, X, d, y, v) — X * Nd_2(S, X, d, y, v)
ElseIf OptionType = «Put» Then
OptionPrice = X * N_d_2(S, X, d, y, v) — S * N_d_1(S, X, d, y, v)
End If
End Function
Function Delta(OptionType, S, X, d, y, v)
If OptionType = «Call» Then
Delta = Application.NormSDist(d_1(S, X, d, y, v))
ElseIf OptionType = «Put» Then
Delta = Application.NormSDist(d_1(S, X, d, y, v)) — 1
End If
End Function
Function Theta(S, X, d, y, v)
T = d / y
Theta = -((S * v * N1d_1(S, X, d, y, v)) / (2 * (T ^ 0.5))) / y
End Function
Function Gamma(S, X, d, y, v)
T = d / y
Gamma = N1d_1(S, X, d, y, v) / (S * (v * (T ^ 0.5)))
End Function
Function Vega(S, X, d, y, v)
T = d / y
Vega = (S * (T ^ 0.5) * N1d_1(S, X, d, y, v)) / 100
End Function
Готовый Excel-файл можно скачать по ссылке.
Теперь в екселевской ячейке можем вызывать любую прописанную нами функцию, например введя в ячейке =OptionPrice(«Put»;76870;90000;13;365;0.47) мы получим теоретическую цену опциона Пут при цене базового актива 76870, страйке 90000, предполагаемой волатильности 45% и за 13 дней до экспирации.
Некоторые моменты, которые хотелось бы отметить
- Полученные в нашей программе значения теорцены практически идентичны тем, что транслирует Мосбиржа, это значит что биржа в своих расчётах использует именно модель БШ.
- На самом деле опцион (как и страховка) не имеет истинной справедливой стоимости — она для каждого своя, и зависит от того какая предполагается волатильность или например какое учитывать число дней (учитывать ли выходные, с каким весом учитывать разные дни недели, сколько дней в году использовать в формуле) и т.д.
- Греки обладают замечательным свойством — чтобы получить значение греков для портфеля фьючерсов и опционов нужно просто сложить соответствующие греки для отдельных активов портфеля. Т.е. мы легко можем рассчитать, например, сколько нужно купить/продать базовых фьючерсов чтобы общая стоимость портфеля не изменялась при изменении цены этого фьючерса (т.н. выравнивание Дельты или дельта-хеджирование).
- Не смотря на свою распространённость, модель БШ основана на допущении, что доходность актива имеет нормальное распределение, что на реальном рынке не выполняется никогда.
Как посчитать проценты в Excel
Почти в каждой сфере деятельности мы сталкиваемся с необходимостью уметь считать проценты. Чаще всего навыки вычисления процентов нам нужны при расчете НДС, маржи, наценки, процентов по кредиту, доходности вкладов и ценных бумаг, скидок. Все эти вычисления производятся как подсчет процента от суммы.
Кликните по кнопке ниже для загрузки Excel файла с примерами расчетов процентов в Excel:
Что такое процент?
Проце́нт (лат. per cent — на сотню) — одна сотая часть. Отмечается знаком «%». Обозначает долю чего-либо по отношению к целому. Например, 25 % от 500 руб. означает 25 частей по 5 руб. каждая, то есть 125 руб.
Базовая формула расчета процента от суммы выглядит так:
(Часть/Целое) * 100 = Процент (%)
Не существует универсальной формулы, подходящей для каждого сценария расчета процентов. Ниже вы узнаете о самых популярных способах расчета.
Как посчитать проценты от суммы в Excel
Видео урок:
Базово, рассчитать процент от суммы в Эксель можно по формуле:
(Часть/Целое) * 100 = Процент (%)
Но если использовать формат ячейки “Процентный”, то для вычисления процента от числа достаточно поделить одно число на другое. Например, у нас есть яблоки, которые мы купили по 100 руб. на оптовом складе, а розничную цену выставим 150 руб. Для того чтобы высчитать процент того, сколько составляет закупочная цена от розничной, нам потребуется:
- Составить таблицу с ценами и добавить колонку для вычисления величины процента:
- В ячейку D2 внести формулу, вычисляющую процент цены закупки от цены продажи:
- Применить формат ячейки D2 “Процентный”:
Как посчитать процент от суммы значений таблицы Excel
Видеоурок:
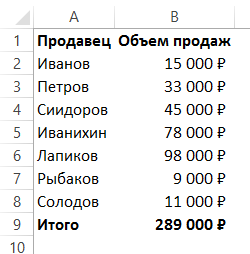
Представим, что у нас есть список продавцов с объемом продаж по каждому и общей суммой всех продаж по всем продавцам. Наша задача определить, какой процент составляет вклад каждого продавца в итоговый оборот:
Для этого нам нужно:
- Добавить колонку к таблице с расчетом процента;
- В ячейку C2 вставить формулу:
Значки $ фиксируют колонку “B” и ячейку “9” для того, чтобы при протягивании формулы на все строки таблицы, Excel автоматически подставлял объем продаж каждого продавца и высчитывал % от общего объема продаж. Если не поставить значки “$”, то при протягивании формулы, система будет смещать ячейку B9 на столько ячеек вниз, на сколько вы протяните формулу.
- Протянуть формулу на все ячейки таблицы, соответствующие строкам с фамилиями продавцов:
- На примере выше мы протянули формулу и получили значения в виде дробных чисел. Для того чтобы перевести полученные данные в проценты выделите данные левой клавишей мыши и смените формат ячеек на “Процентный”:
Как вычислить процент нескольких значений от суммы таблицы
Видеоурок:
На примере выше у нас был список продавцов и их объем продаж. Мы вычисляли какой вклад каждый из работников внес в итоговый объем продаж. Но что, если у нас есть список повторяющихся товаров с данными объема продаж и нам нужно вычислить какую часть конкретный товар составляет в процентах от всех продаж?
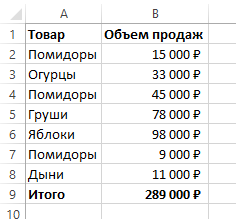
Из списка товаров выше мы хотим вычислить какой объем продаж составляют помидоры (они записаны в нескольких строках таблицы). Для этого:
- Справа от таблицы укажем товар (Помидоры), по которым хотим рассчитать долю в продажах:
- Сменим формат ячейки E2 на “Процентный”;
- В ячейку E2 вставим формулу с функцией СУММЕСЛИ, которая поможет вычислить из списка товаров Помидоры и суммировать их объем продаж, а затем поделить его на общий объем продаж товаров:
Как работает эта формула?
Для расчетов мы используем формулу СУММЕСЛИ. Эта функция возвращает сумму чисел, указанных в качестве аргументов и отвечающих заданным в формуле критериям.
Синтаксис функции СУММЕСЛИ:
=СУММЕСЛИ(диапазон; условие; [диапазон_суммирования])
- диапазон – диапазон ячеек, по которым оцениваются критерии. Аргументом могут быть числа, текст, массивы или ссылки, содержащие числа;
- условие – критерии, которые проверяются по указанному диапазону ячеек и определяют, какие ячейки суммировать;
- диапазон_суммирования – суммируемые ячейки. Если этот аргумент не указан, то функция использует аргумент диапазонв качестве диапазон_суммирования.
Таким образом, в формуле =СУММЕСЛИ($A$2:$A$8;$E$1;$B$2:$B$8)/B9 мы указали “ $A$2:$A$8 ” как диапазон товаров, среди которых функция будет искать нужный нам критерий (Помидоры). Ячейка “ $E$1 ” указана в качестве критерия и указывает что мы ищем “Помидоры”. Диапазон ячеек “ $B$2:$B$8 ” обозначает какие ячейки нужно суммировать, в случае если искомый критерий был найден.
Как посчитать разницу в процентах в Excel
При расчетах в Excel часто требуется посчитать разницу в процентах между двумя числами.
Например, для расчета разницы в процентах между двумя числами А и В используется формула:
(B-A)/A = Разница между двумя числами в процентах
На практике, при использовании этой формулы важно определить какое из нужных вам чисел является “А”, а какое “В”. Например, представим что вчера у вас было в наличии 8 яблок, а сегодня стало 10 яблок. Таким образом количество яблок относительно вчерашнего у вас изменилось на 25% в большую сторону. В том случае, если у вас вчера было 10 яблок, а сегодня стало 8 яблок, то количество яблок, относительно вчерашнего дня сократилось на 20%.
Таким образом, формула, позволяющая корректно вычислить изменения в процентах между двумя числами выглядит так:
Как найти процент между двумя числами из двух колонок в Excel
Видеоурок:
Предположим, что у нас есть цены прошлого и текущего месяца на товары. Наша задача вычислить изменение текущих цен по отношению предыдущим периодам.
Для расчетов нам потребуется формула:
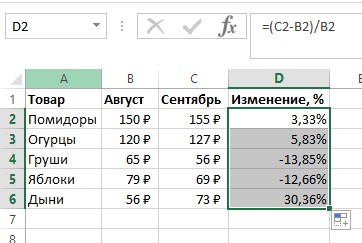
- Протяните формулу на все строки со значениями;
- Измените формат ячейки для колонки “Изменение, %” на “Процентный”.
Как найти процент между двумя числами из двух строк в Excel
В том случае, если у нас есть список в котором в каждой строке указан период с данными продаж и нам нужно вычислить изменения от периода к периоду, то нам потребуется формула:
Где B2 это первая строчка, B3 вторая строчка с данными. После ввода формулы не забудьте отформатировать ячейки с вычислениями как “Процентные”. Выполнив все выше описанные действия, вы получите результат:
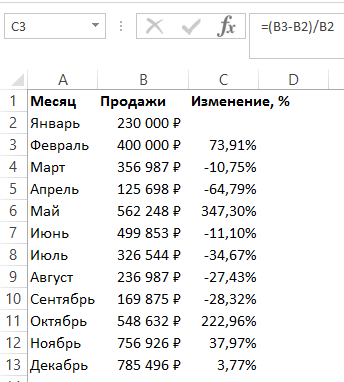
Если у вас есть необходимость вычислить изменения относительно какой-то конкретной ячейки, то важно зафиксировать ее значками “$”. Например, если перед нами стоит задача вычислить изменения объема продаж относительно Января, то формула будет такой:
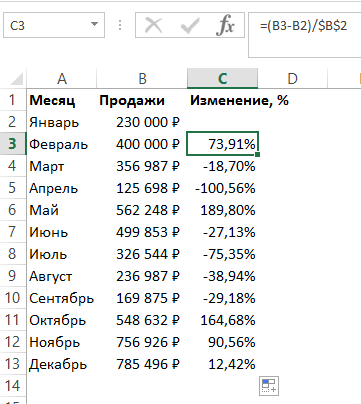
На примере выше значения продаж каждого месяца сравниваются с данными продаж Января.
Как прибавить/вычесть процент к числу в Excel
При расчетах может понадобиться прибавить к какому-либо числу процент. Например, представим, что мы планируем расходы на отпуск. Для того чтобы рассчитать необходимую сумму денег на неделю отпуска, мы закладываем, что в отпуске будем тратить 30% больше чем в обычную рабочую неделю. Для такого расчета нам потребуется формула:
Например, мы хотим прибавить к числу “100” двадцать процентов, тогда формула будет следующая:
Если задача стоит вычесть 20% от числа “100”, то формула выглядит так:
Вернемся к нашей задаче. Запланируем, что на неделю отпуска мы будем тратить на 30% больше чем в регулярную неделю, а неделю после отпуска будем экономить и тратить на 30% меньше чем в неделю до отпуска. Тогда расчет нашего бюджета будет выглядеть так:
Математики любят греческие буквы и используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы символизировать изменение. Когда дело доходит до пары чисел, дельта обозначает разницу между ними. Вы получаете эту разницу, используя основную арифметику и вычитая меньшее число из большего. В некоторых случаях числа располагаются в хронологическом порядке или в некоторой другой упорядоченной последовательности, и вам, возможно, придется вычесть большее из меньшего, чтобы сохранить порядок. Это может привести к отрицательному числу.
Абсолютная Дельта
Если у вас есть случайная пара чисел, и вы хотите узнать дельту – или разницу – между ними, просто вычтите меньшее из большего. Например, дельта между 3 и 6 составляет (6 – 3) = 3.
Если одно из чисел отрицательно, сложите два числа вместе. Операция выглядит следующим образом: (6 – {-3}) = (6 + 3) = 9. Легко понять, почему в этом случае дельта больше, если вы визуализируете два числа на оси x графика. Число 6 равно 6 единицам справа от оси, но отрицательное значение 3 равно 3 единицам слева. Другими словами, он дальше от 6, чем от положительного 3, который находится справа от оси.
Вам нужно запомнить некоторую арифметику вашей начальной школы, чтобы найти дельту между парой дробей. Например, чтобы найти дельту между 1/3 и 1/2, вы должны сначала найти общий знаменатель. Для этого умножьте знаменатели вместе, а затем умножьте числитель в каждой дроби на знаменатель другой дроби. В этом случае это выглядит так: 1/3 x 2/2 = 2/6 и 1/2 x 3/3 = 3/6. Вычтите 2/6 из 3/6, чтобы получить дельту, которая составляет 1/6.
Относительная дельта
Относительная дельта сравнивает разницу между двумя числами, A и B, в процентах от одного из чисел. Базовая формула A – B / A x100. Например, если вы зарабатываете 10 000 долларов в год и жертвуете 500 долларов на благотворительность, относительная дельта вашей зарплаты составляет 10 000 – 500/10 000 x 100 = 95%. Это означает, что вы пожертвовали 5 процентов своей зарплаты, а у вас осталось 95 процентов. Если вы зарабатываете 100 000 долларов в год и делаете то же самое пожертвование, вы сохранили 99, 5% своей зарплаты и пожертвовали только 0, 5% на благотворительность, что не очень впечатляет в момент налогообложения.
От дельты к дифференциалу
Вы можете представить любую точку на двумерном графике парой чисел, которые обозначают расстояние от точки до пересечения осей в направлениях x (горизонтальное) и y (вертикальное). Предположим, у вас есть две точки на графике, называемые точкой 1 и точкой 2, и эта точка 2 находится дальше от пересечения, чем точка 1. Дельта между значениями x этих точек – ∆ x – определяется как (x 2 – x 1), и y для этой пары точек равно (y 2 – y 1). Когда вы делите ∆y на ∆x, вы получаете наклон графика между точками, который говорит вам, как быстро x и y изменяются относительно друг друга.
Склон предоставляет полезную информацию. Например, если вы наносите время вдоль оси x и измеряете положение объекта при его перемещении в пространстве по оси Y, наклон графика показывает среднюю скорость объекта между этими двумя измерениями.
Скорость может быть не постоянной, и вы можете узнать скорость в определенный момент времени. Дифференциальное исчисление обеспечивает концептуальный трюк, который позволяет вам сделать это. Хитрость заключается в том, чтобы представить две точки на оси х и позволить им бесконечно сближаться. Отношение ∆y к ∆x – ∆y / ∆x – при приближении ∆x к 0 называется производной. Обычно это выражается как dy / dx или как df / dx, где f – алгебраическая функция, которая описывает граф. На графике, на котором время (t) отображается на горизонтальной оси, «dx» становится «dt», а производная dy / dt (или df / dt) является мерой мгновенной скорости.
Как рассчитать дельту между двумя числами
Математики любят греческие буквы, и они используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы обозначить изменение. Когда дело доходит до пары чисел, дельта означает разницу м
Содержание
Математики любят греческие буквы, и они используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы обозначить изменение. Когда дело доходит до пары чисел, дельта означает разницу между ними. Вы получаете эту разницу, используя простую арифметику и вычитая меньшее число из большего. В некоторых случаях числа расположены в хронологическом порядке или в другой упорядоченной последовательности, и вам, возможно, придется вычесть большее из меньшего, чтобы сохранить порядок. Это может привести к отрицательному числу.
Абсолютная дельта
Чтобы найти дельту между парой дробей, вам нужно запомнить некоторые из школьных арифметических действий. Например, чтобы найти дельту между 1/3 и 1/2, вы должны сначала найти общий знаменатель. Для этого умножьте знаменатели вместе, а затем умножьте числитель каждой дроби на знаменатель другой дроби. В данном случае это выглядит так: 1/3 x 2/2 = 2/6 и 1/2 x 3/3 = 3/6. Вычтите 2/6 из 3/6, чтобы получить дельту, которая равна 1/6.
Относительная дельта
От дельты к дифференциалу
Наклон дает полезную информацию. Например, если вы наносите время на ось x и измеряете положение объекта во время его перемещения в пространстве по оси y, наклон графика показывает вам среднюю скорость объекта между этими двумя измерениями.
Источник
Дельта Формула
Дельта Формула (Содержание)
Что такое Дельта Формула?
В мире опционов или деривативов термин «дельта» относится к изменению стоимости опциона вследствие изменения стоимости его базового запаса. Другими словами, дельта измеряет скорость изменения стоимости опциона по отношению к движению стоимости базовой акции. Поскольку дельта преимущественно используется для стратегий хеджирования, она также известна как коэффициент хеджирования. Формула для дельты может быть получена путем деления изменения стоимости опциона на изменение стоимости его базового запаса. Математически это представляется как
Примеры формулы дельты (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет Delta.
Давайте возьмем пример товара X, который торговался по 500 долларов на товарном рынке месяц назад, и опцион колл для товара торговался с премией в 45 долларов при цене исполнения в 480 долларов. Сейчас товар продается по цене 600 долларов, а стоимость опциона выросла до 75 долларов. Рассчитать дельту опциона колл на основе предоставленной информации.
Дельта Δ рассчитывается по формуле, приведенной ниже
Давайте возьмем другой пример эталонного индекса, который в настоящее время торгуется на уровне 8000 долларов, в то время как опцион пут на индекс торгуется на уровне 150 долларов. Если индекс торговался по 7800 долларов в месяц назад, тогда как опцион пут торговался по 200 долларов, рассчитайте дельту опциона пут.
Дельта Δ рассчитывается по формуле, приведенной ниже
объяснение
Формула для дельты может быть рассчитана с помощью следующих шагов:
Шаг 3: Затем рассчитайте изменение значения опции, вычтя начальное значение опции (шаг 1) из окончательного значения опции (шаг 2).
Шаг 6: Затем рассчитайте изменение стоимости базового запаса, вычтя его начальное значение (шаг 4) из его окончательного значения (шаг 5).
Шаг 7: Наконец, формула для дельты может быть получена путем деления изменения стоимости опциона (шаг 3) на изменение стоимости базового запаса (шаг 6), как показано ниже.
Актуальность и использование формулы Delta
Калькулятор формулы Delta
Вы можете использовать следующий Delta Calculator
Рекомендуемые статьи
Источник
Кумулятивная дельта
Кумулятивная дельта – в трейдинге это показание индикатора, который считает совокупную разницу между сделками, прошедшими по цене ASK и BID. Кумулятивная дельта показывает разницу между рыночными покупками и продажи.
Дельта – что это простыми словами
В физико-математической науке дельтой является функция, которая отображает разницу между двух и более переменных. Так же, дельтой называется четвёртая буква греческого алфавита, после альфы, беты и гаммы. Именно, исходя из этих истоков, функция дельты записывается в виде треугольника. «Δ»! В сфере трейдинга дельта, как и полагается её формуле, показывает разницу некоторых переменных. А вот разницу, каких именно переменных, это ещё тот вопрос, который требует детального рассмотрения.
Например, дельта по футпринт, показывает разницу рыночных контрактов на покупку и рыночных контрактов на продажу. Ключевым словом здесь выступает прилагательное «рыночных». По причине того, что Market ордера́, сводятся исключительно с Limit заявками, то системе учёта дельты, нет необходимости дублировать объём контрактов. Отсюда вытекает вполне рациональный вывод. Отдельные ячейки, внутри каждого кластера, отображают результат дельт, исключительно ордеров по рынку, они же Market orders!
Внимание! Рекомендую вам ознакомиться с механикой рынка, что бы понять понятие кумулятивной дельты.
В свою очередь гистограмма индикатора дельта, суммирует все рыночные ордера за определённый период времени. Например, если мы используем 15-ти минутный таймфрейм, то бары гистограммы индикатора, отображают общий результат дельты, Market ордеров за 15 минут. Разумеется, что в расчёт дельты, берутся всё те же рыночные ордера. И ровно так же, как и в случае с «кластер дельта», здесь значения дельт, могут быть как положительными, так и отрицательными.
Что же касается такой разновидности дельта индикатора как, «динамический дельта профиль», так здесь всё аналогично. За исключением того, что данный горизонтальный профиль, указывает на преимущество покупателей и продавцов по отдельному ценовому уровню. Да. Вы можете возразить: «Так ведь кластер дельта отвечает за аналогичные результаты»?!
Мы с вами не согласны, так как кластер дельта (дельта по футпринт), отображает результаты разности, лишь за выбранный период времени. То бишь, на 15-ти минутном таймфрейме, отображается дельта по каждому ценовому уровню, только в рамках этих 15-ти минут. Тогда как динамический дельта профиль, суммирует все значения дельт за установленный трейдером временной отрезок!
Кумулятивная дельта основы.
Для кумулятивной дельты имеет ли значение масштаб таймфрейма
Cumulative – переводится как, совокупный, суммарный или накопительный. Из этого определения сразу становится понятно, что данный тип индикатора дельта, что-то накапливает или суммирует. Совершенно верно. Функция дельта с прилагательным «кумулятивная», подразумевает накопление всех дельт, от каждого бара гистограммы за выбранный период времени. И абсолютно не важно, какой масштаб фрейма мы с вами используем при торговле. Вернее важно, но лишь отчасти. Чтобы прояснить картину, рассмотрим один и тот же пример в 2-х вариантах:
Предположим, один из участников рынка, анализирует колебания цен, используя кумулятивную дельту. Важным условием в данном примере, является то, что в качестве фильтра, он использует дневной параметр «накопления». При этом он оптимистично настроен, анализировать и торговать финансовый актив, исключительно на таймфрейме Н1. То есть, его гистограмма индикатора, учитывает «часовые» дельты, с началом открытия биржи.
Теперь представим, что внутридневной трейдер из другого подъезда, так же использует в своей торговле дневную «накопительную» дельту. То есть, его гистограмма индикатора, так же рассчитывает показатели дельт, с момента открытия рынка. И, разумеется, тоже с эффектом «накопления». Но теперь этот персонаж предпочитает работать на 15-ти минутном масштабе. Так, его индикатор кумулятивного эффекта, будет отображать суммируемые значения дельт, относительно его рабочего таймфрейма.
На выше представленном скриншоте, продемонстрированы 2 снимка, которые в точности иллюстрируют придуманные выше примеры. Вопрос; для системы учёта накопительного эффекта, есть ли разница в таймфреймах, для кумулятивной дельты, с охватом расчёта в 1 день? Ответ; и да – есть разница, и нет – не имеет значение для самого индикатора Daily Cumulative Delta! Проясним картину, для полного исключения возможных вопросов и вероятно наивных утверждений, типа: «Как такое вообще может быть»? «Да неее. Так не бывает»!
Накопительный эффект кумулятивной дельты.
Здесь на самом деле всё очень даже просто. Если мы рассматриваем накопительный эффект кумулятивной дельты, относительно заданного параметра, то есть дневного периода. То в этом случае, для самого индикатора, не имеет абсолютно никакого значения, какой масштаб фрейма отображается на данный момент времени. Что при фрейме в 1 час, что при масштабе 15-ти минутных свеч. Дневная кумулятивная дельта, всё равно будет производить расчёты за весь текущий день.
Источник
Примеры работы функции ДЕЛЬТА для сравнения двух чисел в Excel
Функция ДЕЛЬТА в Excel используется для проверки двух числовых значений и возвращает два возможных варианта:
Примеры использования функции ДЕЛЬТА в Excel
Пример 1. В таблице Excel указаны значения независимой координаты X и значения зависимых координат Y1 и Y2 для двух разных функций. Определить количество пар совпадающих значений.
Вид исходной таблицы данных:
Для решения задачи сравним каждую пару значений зависимых координат Y1 и Y2 с помощью функции ДЕЛЬТА. В ячейке D3 запишем следующую формулу:
Полученное значение (1) свидетельствует о равенстве сравниваемых чисел. Протянем записанную в ячейке D3 формулу вниз до ячейки D12, чтобы автоматически рассчитать результаты для остальных значений Y1 и Y2:
Для расчета числа пар совпадающих значений используем следующую функцию:
Всего 4 пары совпадений в значениях функций координат.
Калькулятор сроков возврата инвестиций в банковские депозиты
Пример 2. Реализовать калькулятор, который рассчитывает, сколько времени потребуется на получение определенной прибыли от депозита при известной начальной сумме вклада и годовой процентной ставки. Предусмотреть вывод сообщения об ошибке в случае, если одно или несколько исходных данных не указаны.
Вид формы для расчета:
Поскольку для расчета используется логарифм из частного ожидаемой и начальной суммы с основанием в виде суммы депозита, выраженного в процентах (то есть 100%), и процентной ставки, то каждая ячейка из диапазона B2:B4 не должна являться пустой или принимать значение 0, поскольку логарифм нуля или логарифм с основанием 1 (100%) не может быть вычислен. Поэтому для расчетов используем следующую формулу:
В качестве проверочного выражения функции ЕСЛИ выступает значение, являющееся суммой возвращаемых результатов функциями ДЕЛЬТА. Последние сравнивают значения, содержащиеся в ячейках B2, B3 и B4 соответственно с 0 (второй аргумент явно не указан). Данный вариант записи соответствует логическому И (общий результат равен ИСТИНА, если все выражения, проверяемые функцией И, возвращают результат ИСТИНА). Полученное значение (0 или любое число от 1 до +∞) будет интерпретировано как ЛОЖЬ или ИСТИНА соответственно.
При незаполненных полях получим следующий результат:
Напишем формулу для преобразования дробного числа в годы и месяцы:
В результате получим:
Расчет вероятности выпуска бракованной продукции на производстве в Excel
Пример 3. При изготовлении деталей на производственно-ремонтном заводе существует вероятность брака производимой продукции, которая равная коэффициенту 0,001. Определить, какая вероятность появления 10 выбракованных деталей (в этом случае вся партия считается браком) в партии из 35000 шт. Считается, что вероятностями ниже 10% можно пренебречь (то есть их приравнивают к нулю).
Вид исходной таблицы данных:
Для расчета используем следующую формулу:
Функция ОКРУГЛВНИЗ округляет до 0 все значения, которые меньше числа 0,01, то есть 10%-й вероятности. Функция ДЕЛЬТА принимает только один аргумент (выражение, полученное на основе формулы Пуассона для вычисления маловероятных случайных ситуаций), то есть сравнение выполняется с числом 0 (нуль).
Если вычислять формулу поэтапно, будет видно, что вероятность по формуле Пуассона равна примерно 0,00974 число1 ;[число2])
Источник
Как работать с Дельтой?
Если говорить просто, то дельта – это разница между объёмами рыночных покупок и рыночных продаж за период времени. Этот термин вошёл в лексикон трейдеров в 2002 году, вместе с изобретением биржевого графика Футпринт и переходом трейдинга на цифровые платформы. Сегодня этот инструмент широко используется среди биржевых торговцев. В этой статье мы рассмотрим некоторые особенности этого индикатора и узнаем, как работать с Дельтой, чтобы улучшить торговую стратегию.
Дельта – суть и классификация
Чтобы понять суть термина Дельта, необходимо разобраться, из каких элементов она состоит. Известно, что на бирже есть, так называемые, агрессивные продавцы и агрессивные покупатели. Для упрощения классификации, сделки, которые инициируются агрессивными покупателями, торгуются по цене Ask, а сделки, проторгованные по инициативе агрессивных продавцов – по цене Bid.
Дельта же – это разница между этими двумя проторгованными объёмами. Чтобы рассчитать Дельту, необходимо от объёмов торговли по цене Ask отнять объёмы торговли по цене Bid. Дельта рассчитывается именно по рыночным, а не по лимитным ордерам, поскольку они бы только дублировали объёмы и усложнили задачу трейдеру.
Футпринт – детализация рынка
График Футпринт позволяет, образно говоря, препарировать каждый бар и увидеть, как изменялось значение Дельты внутри него. Для удобства визуализации, положительная Дельта (с преобладанием объёмов покупок) окрашивается зелёным цветом, причём, чем темнее оттенок, тем сильнее в конкретный момент были покупатели. Аналогично, отрицательная Дельта (с преобладанием объёмов продаж) на графике выкрашена в красный цвет, и чем темнее оттенок, тем интенсивнее велись продажи актива.
Что это знание даёт трейдеру? Возможность анализировать и делать более точные прогнозы. Поскольку поток ордеров и движение цены на рынке тесно взаимосвязаны, анализ графика Футпринт и Дельты может помочь трейдеру сориентироваться в текущей рыночной ситуации и принять верное решение.
Индикатор Дельта – читаем между строк
Увидеть индикатор Дельта можно в нижней части графика под каждым отдельным баром – н показывает суммарное значение Дельты для каждого из них. Также как и на графике Футпринт, здесь есть два цвета, показывающие преобладание отрицательного (продажи), либо положительного (покупки) потока ордеров.
Довольно часто именно индикатор Дельта позволяет внимательному трейдеру правильно интерпретировать рыночные движения, поскольку нередки случаи, когда при положительном потоке ордеров цена падает, а при отрицательном – растёт.
Подобные несостыковки ярко свидетельствуют о вмешательстве третьей силы – мощных рыночных игроков с большими капиталами. Если наблюдается падение цены при положительной Дельте, это означает, что крупный игрок защищает все свои рыночные продажи лимитными ордерами, тем самым без особых усилий и необходимости открывать дополнительные позиции толкает цену в нужном ему направлении.
Подобным образом действия биржевого крупняка прослеживаются и при преобладании отрицательной Дельты на растущей цене.
Внимательный взгляд на Дельту поможет трейдеру «читать между строк» — видеть поведение крупных игроков и замечать, а также прогнозировать истинный тренд, тогда как те, кто ориентируется исключительно на кривую цен, могут быть легко вытряхнуты из рынка.
Как работать с Дельтой – внимание к мелочам
Чтобы получить от этого ценного инструмента максимум пользы, нельзя пренебрегать показателями Дельты во время проведения технического анализа. При этом можно использовать и график Футпринт, и индикатор Дельта на каждом баре, и кумулятивную Дельту, отображающую суммарную Дельту за период времени, например, за торговую сессию.
Порой именно показатели Дельты способны дать трейдеру оптимальную точку для входа в рынок. К примеру, по длине отрицательной Дельты можно определить момент окончания периода накопления и войти в сделку прямо перед началом крупного восходящего тренда.
Чтобы научиться, как работать с Дельтой правильно и прибыльно для своей торговли, можно пройти курс в Школе трейдинга Александра Пурнова под руководством опытного наставника. Кроме того, после подписки на наш блог будут доступны ценные материалы на тематику трейдинга и финансов.
Источник
