Как найти дельту радиуса

ndehost

+20

Решено

2 года назад

Физика

Студенческий

Дельта r в физике.
Как найти дельта r, если есть известное r действительное и r измеренное ?
И как найти их % погрешности&

Смотреть ответ

Ответ

0
(0 оценок)

1

Dedagenn
2 года назад

Светило науки – 5327 ответов – 32035 раз оказано помощи

Ответ:

абсолютная погрешность величины Х есть разность ∆Х=Хизм-Хдейств;

относительная погрешность dX=∆X/Xдейств *100%

(0 оценок)

Остались вопросы?

Новые вопросы по предмету Физика

Помогите решить задачи.1)Автобус,двигаясь со скоростью 72км/ч,начинает тормозить с ускорением 3м/с2 и останавливается. Чему равно время торможе …

ДАЮ 60 БАЛЛОВШкольник решил испытать кастрюлю на плавучесть. Он поместил цилиндрическую кастрюлю массой 2.4 кг, высотой 30 см и площадью дна 8 …

Прямолинейное движение двух тел задано уравнениями x1(t) = k1t + b1 и x2(t) = k2t+ b2, где x1(t) и x2(t) – координаты в момент времени t первог …

СРОЧНО!! ДАЮ 30 БАЛЛОВЭкспериментатор Глюк добыл немного неизвестного науке вещества в твёрдомсостоянии, поместил его в калориметр и радостно н …

Движение точки на ободе колеса радиусом R, катящегося с угловой скоростью ω без скольжения по горизонтальной поверхности описывается уравнениям …

Мммаашшаа_zn


13 Апр, 18

Вектор дельта r это

В кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси.

1. Векторный способ.

В этом способе положение материальной точки `A` задаётся с помощью так называемого радиус-вектора `vecr`, который представляет собой вектор, проведённый из точки `O`, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку `A` (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени `vecr=vecr(t)`.

Геометрическое место концов радиус-вектора `vecr(t)` называют траекторией точки `A`.

В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка `A` после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.

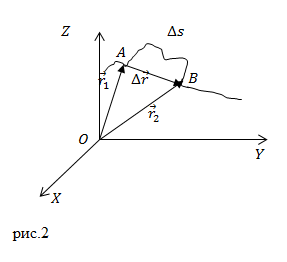
Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени `Delta t` тело (точка `A`) переместилось из начального положения `1` с радиус-вектором `vec r_1` в конечное положение `2` с радиус-вектором `vec r_2` (рис. 2). Приращение `Deltavec r` радиус-вектора тела в таком случае равно: `Deltavec r = vec r_2- vec r_1`.

Вектор `Deltavec r`, соединяющий начальное и конечное положения тела, называют перемещением тела.

Отношение `Delta vec r//Delta t` называют средней скоростью (средним вектором скорости) `vec v_”cp”` тела за время `Delta t`:

`vecv_”cp”=(Deltavecr)/(Delta t)` (1)

Вектор `vecv_”cp”` коллинеарен и сонаправлен с вектором `Deltavec r`, так как отличается от последнего лишь скалярным неотрицательным множителем `1//Delta t`.

Предложенное определение средней скорости справедливо для любых значений `Delta t`, кроме `Delta t=0`. Однако ничто не мешает брать промежуток времени `Delta t` сколь угодно малым, но отличным от нуля.
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени `t` или в конкретной точке траектории. С этой целью промежуток времени `Delta t` устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение `Delta vec r`. При этом отношение `Deltavec r//Delta t` стремится к определённому значению, не зависящему от `Delta t`.

Величина, к которой стремится отношение `Deltavec r//Delta t` при стремлении `Delta t` к нулю, называется мгновенной скоростью`vec v`:

`vec v =(Delta vec r)/(Delta t)` при `Delta t -> 0`.

Теперь заметим, что чем меньше `Delta t`, тем ближе направление `Deltavec r` к направлению касательной к траектории в данной точке. Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела.

В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости `vec v` тела (материальной точки).

Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения. Его определяют через отношение приращения вектора скорости `Delta vec v` тела к промежутку времени `Delta t`, в течение которого это приращение произошло.

Ускорением `veca` тела называется величина, к которой стремится отношение `Delta vec v//Delta t` при стремлении к нулю знаменателя `Delta t`:

`vec a =(Delta vec v)/(Delta t)` при `Delta t -> 0` (2)

При уменьшении `Delta t` ориентация вектора`Delta vec v` будет приближаться к определённому направлению, которое принимается за направление вектора ускорения `vec a`. Заметим, что ускорение направлено в сторону малого приращения скорости, а не в сторону самой скорости!

Напомним, что в системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр в секунду (`”м”//”с”`) и метр на секунду в квадрате ( `”м”//”с”^2`).

2. Координатный способ.

В этом способе положение материальной точки `A` на плоскости в произвольный момент времени `t` определяется двумя координатами `x` и `y`, которые представляют собой проекции радиус-вектора $$ overrightarrow$$тела на оси `Ox` и `Oy` соответственно (рис. 3). При движении тела его координаты изменяются со временем, т. е. являются функциями `t`: $$ x=xleft(tright)$$ и $$ y=yleft(tright)$$. Если эти функции известны, то они определяют положение тела на плоскости в любой момент времени. В свою очередь, вектор скорости $$ overrightarrow$$ можно спроецировать на оси координат и определить таким образом скорости $$ _$$ и $$ _$$ изменения координат тела (рис. 4). В самом деле $$ _$$ и $$ _$$ будут равны значениям, к которым стремятся соответственно отношения `Delta x//Delta t` и `Delta y//Delta t` при стремлении к нулю промежутка времени `Delta t`.

3. Естественный (или траекторный) способ.

Этот способ применяют тогда, когда траектория материальной точки известна заранее. На заданной траектории `LM` (рис. 5) выбирают начало отсчёта – неподвижную точку `O`, а положение движущейся материальной точки `A` определяют при помощи так называемой дуговой координаты `l`, которая представляет собой расстояние вдоль траектории от выбранного начала отсчёта `O` до точки `A`. При этом положительное направление отсчёта координаты `l` выбирают произвольно, по соображениям удобства, например так, как показано стрелкой на рис. 5.

Движение тела определено, если известны его траектория, начало отсчёта `O`, положительное направление отсчёта дуговой координаты `l` и зависимость $$ lleft(tright)$$.

Следующие два важных механических понятия – это пройденный путь и средняя путевая скорость.
По определению, путь `Delta S` – это длина участка траектории, пройденного телом за промежуток времени `Delta t`.

Ясно, что пройденный путь – величина скалярная и неотрицательная, а потому его нельзя сравнивать с перемещением `Delta vec r`, представляющим собой вектор. Сравнивать можно только путь `Delta S` и модуль перемещения `
|Delta vecr|`. Очевидно, что `Delta S >=|Deltavec r|`.

Средней путевой скоростью `v_”cp”` тела называют отношение пути `Delta S` к промежутку времени `Delta t`, в течение которого этот путь был пройден:

`v_”cp”=(Delta S)/(Delta t)` (3)

Определённая ранее средняя скорость `v_”cp”` (см. формулу (1)) и средняя путевая скорость отличаются друг от друга так же, как `Deltavec r` отличается от `Delta S`, но при этом важно понимать, что обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения `Delta t`. Само слово «средняя» означает усреднение по времени.

Городской троллейбус утром вышел на маршрут, а через 8часов, проехав в общей сложности `72` км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость `vec v_”cp”` и средняя путевая скорость `v_”cp”` троллейбуса?

Поскольку начальное и конечное положения троллейбуса совпадают, то его перемещение `Delta vecr` равно нулю: `Deltavecr=0`, следовательно, `vecv_”ср”=Deltavecr//Deltat=0` и `|vecv_”ср”|=0`. Но средняя путевая скорость троллейбуса не равна нулю:

`v_”cp”=(Delta S)/(Delta t)=(72 “км”)/(8 “ч”)=9 “км”//”ч”`.

Путь и перемещение

При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.

Путь – длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь – это скалярная величина.

При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:

где $x_1$ – координата начального положения тела; $x_2$ – конечная координата тела.

Его можно вычислить, если известен модуль скорости ($v=v_x$):

[Delta s=vt left(2right),]

где $t$ – время движения тела.

Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.

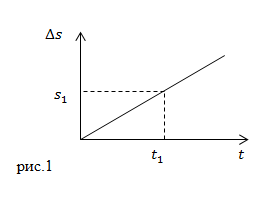
Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку $<Delta s>_1$, которая соответствует пройденному пути за время от $t=0 c$ до $t_1$.

Путь не бывает меньше нуля и не может уменьшаться при движении тела.

Перемещение

Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:

[Delta overline=overlineleft(t+Delta tright)-overlineleft(tright)left(3right).]

Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.

Приращение радиус-вектора материальной точки – это перемещение ($Delta overline$).

В декартовой системе координат радиус-вектор точки представляют в виде:

где $overline$, $overline$,$ overline$ – единичные орты осей X,Y,Z. Тогда $Delta overline$ равен:

[Delta overline=left[xleft(t+Delta tright)-xleft(tright)right]overline+left[yleft(t+?tright)-yleft(tright)right]overline+left[zleft(t+?tright)-zleft(tright)right]overlineleft(5right).]

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:

[left|Delta overlineright|=Delta s left(6right).]

Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overlineright|$ или просто $Delta r$ (без указания стрелки).

Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:

Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.

Примеры задач на путь и перемещение

Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?

Решение: Сделаем рисунок.

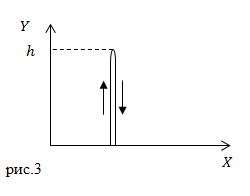
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь – длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:

Перемещение – направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:

Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$

Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?

Решение: Сделаем рисунок.

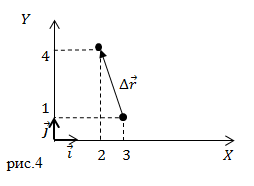
Радиус – вектор начальной точки запишем как:

Радиус – вектор конечной точки имеет вид:

Вектор перемещения представим как:

Из формулы видим, что:

[Delta r_x=-1;;Delta r_y=3. ]

Ответ: $Delta r_x=-1;;Delta r_y=3 $

Перемещение. Перемещение точки

Понятие перемещения имеет важнейшее значение в кинематике.

Мы будем рассматривать перемещение точки.

Зададим положение точки с помощью радиус-вектора.

Вектор перемещения равен приращению радиус-вектора.

на картинке дельта «эр» – это и есть вектор перемещения.

По правилу сложения векторов имеем:

а это значит, что вектор перемещения равно приращению радиус-вектора.

[spoiler title=”источники:”]

http://www.webmath.ru/poleznoe/fizika/fizika_88_put_i_peremeshhenie.php

Перемещение. Перемещение точки

[/spoiler]