Как найти дельту в термодинамике

Физическая дисциплина «Термодинамика», имеющая дословный перевод с греческого как θέρμη — «тепло», δύναμις — «сила», занимается изучением общих характеристик макросистем и обращения энергии внутри них. Эту науку относят к феноменологическому типу, хотя опирается она на факты, полученные опытным путем.

Термодинамическая система, рассматриваемая в данном ракурсе, имеет конкретные характеристики, не применимые к единичным атомам и молекулам. К ним относят температуру, энергию, объем, концентрацию растворов, давление.

Определение таких параметров происходит по формулам термодинамики.

Основные формулы термодинамики

Особенностью термодинамики является то, что ее постулаты не касаются взаимодействия отдельных единиц (атомов, молекул), как в молекулярной физике. Предметом изучения предстают общие взаимопревращения энергии, образование теплоты, теплопередача и совершение работы.

Исходя из этого, выделяют основные формулы термодинамики, к которым относятся:

1. Уравнение Менделеева-Клайперона: (PV=(m/M)*RT). Его смысл — в изменениях трех входящих величин, которые направлены на характеристику состояния идеального газа.
2. Количество вещества, обозначаемое буквой (ν). (nu=N/NA=m/mu)

   Величина, выражающая, сколько одинаковых структурных компонентов (единиц) находится в веществе.

3. Закон Дальтона: давление смеси газов на стенку сосуда равно сумме давлений каждого входящего в смесь элемента: (p=p1+p2+…pn.)
4. Главное уравнение МКТ (молекулярно-кинетической теории): (p=2n/3<varepsilon>n=N/V). Выражает математическое соотношение таких параметров, как давление газа и микропараметров: массы молекул, их скорости движения, концентрации.
5. Средняя кинетическая энергия поступательного движения молекулы газа. Для обозначения применяется (E_k),  выражается через формулу: (E_k=E_{моля}/NA=3/2ast RT/NA). Ее мерой является абсолютная температура идеального газа, поскольку потенциальная энергия (вследствие взаимодействия молекул друг с другом) равна нулю. Зная, что R/N_A=k, получается формула: (E_k=3/2ast kT).
6. Давление идеального газа прямо пропорционально концентрации и его температуре: (P=nkT.)
7. Скорость молекул определяется по формулам:
   (V=surd(2kT/m_o)=surd(2RT/mu)) — наиболее вероятная;
   (<V>=surd(8kT/pi m_o)=surd(8RT/pimu)) — среднеарифметическая;
   (<Vкв>surd(3kT/m_o)=surd(3RT/mu)) — средняя квадратичная.
8. Сумма кинетических энергий всех молекул определяет внутреннюю энергию всего идеального газа. Математически выражение выглядит так: (U=i/2ast(m/mu)ast RT.)
9. Формула для определения работы, которую совершает идеальный газ при расширении:( A=P(V_2-V_1).)
10. Формула первого закона термодинамики: (Q=Delta U+A.)
11. Для определения удельной теплоемкости вещества применяется математическое выражение: (С=Delta Q/mdT.)
12. Кроме удельной теплоемкости, существует понятие молярной теплоемкости. Для ее определения применяется формула: (C=cmu). Для изохорного процесса правильная формула принимает вид: (C_v=1/2ast R), для изобарного: (C_p=((i+2)/2)ast R).

Первое начало термодинамики

Согласно первому закону термодинамики, (Q) (количество внутренней теплоты), которое получил газ извне, расходуется на совершение работы (А) и изменение внутренней энергии (U). Формула закона: (Q=Delta U+A).

На практике газ может быть нагрет либо охлажден. Однако в данном случае рассматривается изотермический процесс, в котором один из характеризующих параметров остается неизменным.

Если процесс изотермичен, в химии включается закон Бойля-Мариота. В нем говорится, что давление газа соотносится к изначальному объему, при стабильной температуре, обратно пропорционально.

(Q=A)

Когда процесс происходит при неизменном объеме, говорят об изохорности. Здесь вступает в действие закон Шарля. В обозначенных условиях то тепло, которое поступило к газу, расходуется на изменение внутренней энергии. Другими словами, (P) пропорционально (T).

(Q=Delta U)

Протекание процессов в идеальном газе при неизменном давлении носит характер изобарного. Здесь действует закон Гей-Люссака, который выражается уравнением:

(Q=Delta U=pDelta V)

Полная формулировка закона гласит: полученное тепло при изобарном процессе расходуется на совершение работы газом, а также изменяет его внутреннюю энергию.

Часть процессов происходят изолированно от внешней среды. Газ не получает дополнительной энергии. Такая ситуация носит название адиабатной и математически записывается: (Q=0). Работа (А) в таком случае выражается: (A=-Delta U.)

Уравнение идеального газа в термодинамике

Молекулы идеального газа постоянно движутся. От того насколько велика скорость их движения, зависит общее состояние газа, а также величина его воздействия, например, на стенки сосуда. Поэтому одним из основных уравнений термодинамики является Клайперона-Менделеева:

(PV=(m/M)ast RT)

В уравнении (m) — единица массы газа, (M) — его молекулярная масса, (R) — универсальная величина, называемая газовой постоянной. Ее значение = 8,3144598. Измеряется в Дж/(моль*кг).

В основе термодинамики лежат и другие газовые постоянные, например, число Авогадро, постоянная Больцмана. Таким образом, (R=kNA.)

Из уравнения Клайперона-Менделеева можно также вычислить массу. Она будет равна произведению плотности на объем: (m=rho V).

Основное уравнение молекулярно-кинетической теории (МКТ)

Решение части задач зависит от знания особенностей взаимосвязи между давлением газа и характеристикой кинетической энергии его молекул. Математическое выражение такой зависимости носит название основного уравнения МКТ:

(p=2/3ast nE)

В данном выражении кинетическая энергия обозначена буквой (Е), а концентрация молекул — (n). Каждую из этих величин физики можно найти исходя из соответствующих формул, после чего уравнение для молекулярно-кинетической теории (МКТ) приобретает вид:

(p=nkT)

Формула теплоемкости и главная формула КПД в термодинамике

Когда теплообмен проявляется передачей телу определенного количества теплоты, его энергия, как и температура, меняются.

То количество теплоты, обозначаемое (Q), которое понадобится для того, чтобы 1 кг определенного вещества нагреется на 1 К, носит определение теплоемкости вещества и обозначается с.

Математическое выражение относительно переданного количества теплоты выглядит формулой:

(Q=cm(t_2-t_1)=cmDelta t)

Измеряется величина в Дж/(кг∙К).

При t2⟩t1, количество теплоты со знаком плюс, следовательно, вещество нагревается. Если наоборот, то Q — со знаком минус, и вещество остывает.

В физике, характеризуя свойства вещества, говорят о его теплоемкости. Это имеет значение, например, при выборе стройматериалов или сырья для изготовления нагревательных приборов. Теплоемкость равна произведению массы на удельную теплоемкость данного тела:

(C=cm)

Учитывая, что в величине теплоемкости уже отражена масса, то сокращенная формула для определения (Q) выглядит так:

 (Q=C(t_2-t_1))

С другой стороны, то количество теплоты, которое отдает источник, можно высчитать по формуле: 

(Q=Pt.)

В выражении буквой (P) обозначается мощность нагревателя, а (t) — время их контакта.

Конструкция, состоящая из нагревателя, тела-реципиента теплоты и охладителя, носит название тепловой машины. В качестве примера рассматривается двигатель внутреннего сгорания. Как и любой механизм, она имеет такую характеристику, как КПД — коэффициент полезного действия. Для его расчета применяется формула:

(eta=(Q_н-Q_x)/Q_н)

Внутренняя энергия одноатомного и двухатомного идеального газа

Характерной особенностью идеального газа является отсутствие у его составляющих частей потенциальной энергии. Вся внутренняя энергия — это сумма кинетических энергий всех молекул. Она является величиной, прямо пропорциональной температуре идеального газа:

(mw2/2=alpha T)

В этом уравнении:

(alpha T=3Rmu/2Nmu)

Исходя из приведенных формул, величина кинетической энергии поступательного движения идеального газа должна определяться исходя из выражения:

(mv2/2=(3Rmu/2Nmu)ast T)

Поступательное движение характеризуется тремя степенями свободы. На каждую из них приходится одна треть общей кинетической энергии.

Двух- и более атомные молекулы газа характеризуются степенями свободы, касающимися вращательного движения.

Если обозначить число молекул в одном киломоле за (Nμ), то внутренняя энергия идеального газа будет измеряться по формуле:

(Umu=1/2(Rmu Ti))

В формуле (i) — число степеней свобод.

Если газ одноатомный, (i=3), двуатомный — 5, трех- и более — 6.

Задачи на термодинамику характеризуют распространенные физические процессы, поэтому часть включаются в программы экзаменов. Если для их решения не хватает времени, можно обратиться за помощью в Феникс.Хелп. На профильном сайте вам помогут справиться с любой, даже запутанной задачей, экономя ваши время и силы.

Unit Converter

Enter the initial temperature and final temperature of a substance or object to calculate the delta T.

• Mixed Air Temperature Calculator
• Change in Internal Energy Calculator
• Thermal Energy Calculator

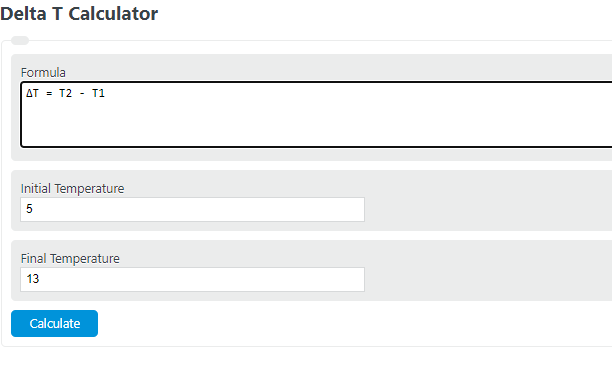
Delta T Formula

The following formula is used to calculate delta T.

• Where ΔT is the change in temperature (delta T)
• T2 is the final temperature
• T1 is the initial temperature

To calculate delta T, simply subtract the initial temperature from the final temperature.

Delta T Definition

Delta T, denoted ΔT, is the term and symbol used to describe the change in temperature of a substance, system, or object. the delta in delta T is the term used to describe the change in and the T denotes temperature.

Delta T Example

How to calculate delta T?

1. First, determine the initial temperature.

   Measure the initial temperature of the material.

2. Next, determine the final temperature.

   Measure the final temperature of the material over the time period.

3. Finally, calculate the delta T.

   Calculate the change in temperature by subtracting the initial temperature from the final temperature.

FAQ

What is delta?

Delta is a symbol used in mathematics and science to describe the change in a value. For example ΔT is the change in temperature while ΔP is the change in pressure and so forth.

---

Термодинамические функции (потенциалы)

Термодинамические потенциалы – это функции определенных наборов термодинамических параметров, позволяющие находить все термодинамические характеристики системы как функции этих параметров.
Рассматриваемые в формулировках процессы предполагаются обратимыми.

Внутренняя энергия

U = U(S,V)

dU = TdS – PdV

T = (дельта U/дельта S)_V

P = -(дельта U/дельта V)_S

Изменение внутренней энергии равно работе, совершенной над системой в адиабатическом процессе, или теплоте, полученной системой в изохорическом процессе.

Энтальпия

(тепловая флуктуация)
H = U + PV

H = H(S, P)

dH = TdS + VdP

T = (дельта H/дельта S)_P

V = (дельта H/дельта P)_S

Изменение энтальпии равно теплоте, полученной системой в изобарическом процессе.

Свободная энергия Гельмгольца

F = U – TS

F = F(T,V)

dF = – SdT – PdV

S = (дельта F/дельта T)_V

P = -(дельта F/дельта V)_T

Изменение свободной энергии равно работе, совершенной над системой в изотермическом процесе.

Термодинамический потенциал Гиббса

Ф = U+PV-TS

Ф = Ф(Т, Р)

dФ = -SdT+VdP

S = -(дельта Ф/дельта T)_P

V = (дельта Ф/дельта P)_T

Вывод соотношений

ню = 1 моль, C_V = const:

1) U = U(S,V)

U = C_V T (для ид.газа)

S = S0 + C_V ln (T/T0) + R ln (V/V0) – энтропия ид.газа

=> T = T0 e^[(S-S0)/C_V] (V/V0)^(-R/C_V) = const*e^(S/C_V) V^(-j+1)

2) H (S; P)

H = C_P T (для ид.газа)

Перепишем выражение для энтропии, используя уравнение состояния идеального газа

S = S0 + C_P ln (T/T0) – R ln (P/P0)

T = T0 e^[(S-S0)/C_V] * (P/P0)^(R/C_P); R/C_P = (гамма-1)/гамма.

H (S;P) = TC_P = C_P T0 e^[(S-S0)/C_P]*(P/P0)^[(гамма-1)/гамма] = const * e^(S/C_P) P^[(гамма-1)/гамма]

3) F = U – TS

F = C_V T – TS = -RT ln (V/V0 * (T/T0)^(C_V/R) * e^((S0-C_V)/R))

C_V = 3/2 R: F = -RT/2 ln (AV^2T^3), где А – константа

4) Ф = U – TS + PV = U – TS + RT

Ф = C_V T – TS + RT = C_P T – TS = -RT ln (P/P0 * (T/T0)^(C_P/R) * e^((S0-C_P)/R))

Для одноатомного газа: Ф = -1/2 RT ln(BP^-2T^5), где B – константа.

Соотношения Максвелла

(дельта T/дельта V)_S = дельта^2 U/(дельта V дельта S) = -(дельта P/дельта S)_V; (дельта T/дельта P)_S = дельта^2 H/(дельта P дельта S)_P

(дельта S/дельта V)_T = -дельта^2 F/(дельта V дельта T) = (дельта P/дельта T)_V; (дельта S/дельта P)_T = дельта2 Ф/(дельта P дельта T) = -(дельта V/дельта T)_P

(дельта U/дельта V)_T = T(дельта P/дельта T)_V – P

CdT = dU + PdV = (дельта U/дельта T)_V dT + [(дельта U/дельта V)_T + P]dV

C_P – C_V = [(дельта U/дельта V)_T + P](дельта V/дельта T)_P

C_P – C_V = T(дельта P/дельта T)_V (дельта V/дельта T)_P = -T [(дельта V/дельта T)_P]^2/(дельта V/дельта P)_T

(дельта P/дельта T)_V = (дельта P/дельта V)_T (дельта V/дельта T)_P

C_P – C_V = R.

Основные формулы термодинамики и молекулярной физики, которые вам пригодятся. Еще один отличный день для практических занятий по физике. Сегодня мы соберем вместе формулы, которые чаще всего используются при решении задач в термодинамике и молекулярной физике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Итак, поехали. Попытаемся изложить законы и формулы термодинамики кратко.

Идеальный газ

Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.

Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.

Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева

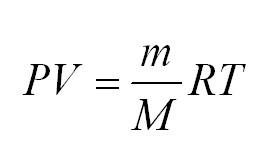
Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).

Универсальная газовая постоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)

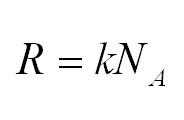
Массу, в свою очередь, можно вычислить, как произведение плотности и объема.

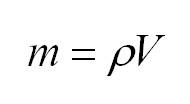
Основное уравнение молекулярно-кинетической теории (МКТ)

Как мы уже говорили, молекулы газа движутся, причем, чем выше температура – тем быстрее. Существует связь между давлением газа и средней кинетической энергией E его частиц. Эта связь называется основным уравнением молекулярно-кинетической теории и имеет вид:

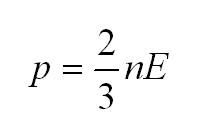
Здесь n – концентрация молекул (отношение их количества к объему), E – средняя кинетическая энергия. Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:

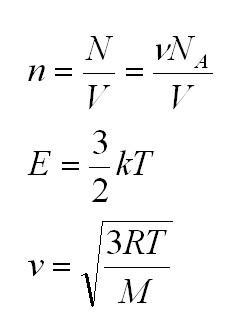
Подставим энергию в первое уравнение, и получим еще один вид основного уравнения МКТ

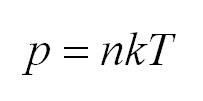
Первое начало термодинамики. Формулы для изопроцессов

Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:

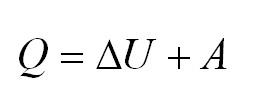
Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:

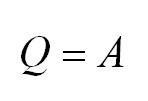
Изохорный процесс протекает при постоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.

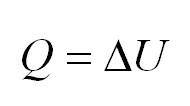
Изобарный процесс идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.

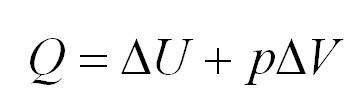
Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:

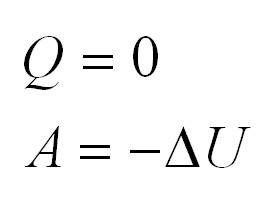
Внутренняя энергия одноатомного и двухатомного идеального газа

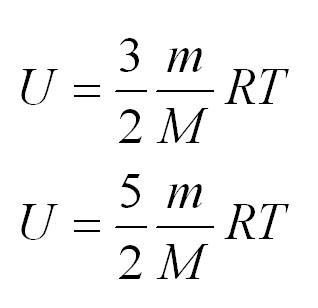
Теплоемкость

Удельная теплоемкость равна количеству теплоты, которое необходимо для нагревания одного килограмма вещества на один градус Цельсия.

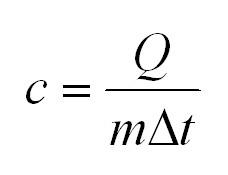
Помимо удельной теплоемкости, есть молярная теплоемкость (количество теплоты, необходимое для нагревания одного моля вещества на один градус) при постоянном объеме, и молярная теплоемкость при постоянном давлении. В формулах ниже, i – число степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного – 5.

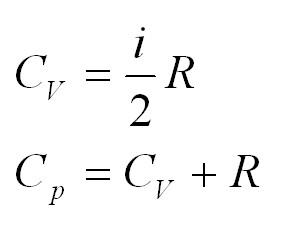
Тепловые машины. Формула КПД в термодинамике

Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.

Коэффициент полезного действия тепловой машины вычисляется по формуле

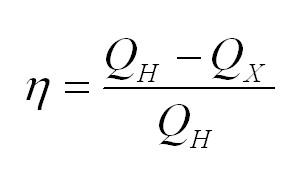
Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы  – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.

В физике и некоторых других науках греческой буквой D («дельта») принято обозначать разницу между определенными параметрами. Это могут быть, например, температура, время, давление, длины отрезков, расстояния между координатами по одной и той же оси и т.д. Латинской буквой t чаше всего обозначают время и температуру.

Вам понадобится

• – данные измерений;
• – калькулятор.

Инструкция

Если буквой t в данном разделе физики обозначается температура, проведите измерения температуры. Термометр может быть любым. Нужно, чтобы его шкала соответствовала нужной вам степени точности. Разумеется, измерять оба показателя необходимо по одному и тому же термометру.

Второй показатель зависит от условий задачи. Например, если вам нужно отследить изменение состояния объекта, снимите второй показатель через некоторое время. Самый доступный эксперимент – измерить температуру своего тела утром и вечером. Вычтите из большего числа меньшее. Это и будет дельта t. Поскольку температура с течением времени может как увеличиваться, так и уменьшаться, вам нужен модуль разности.

В задаче может быть предложено и сравнение изменений разных объектов. Дельта t в этом случае приобретает несколько иной смысл, но все равно она остается разностью температур. Например, вам нужно определить, насколько нужно разогреть горелку, чтобы расплавить два разных металла. Сравните температуры плавления одного и другого вещества. Точно так же, как и в первом случае, вычтите из большего показателя меньший. Если вы проводите эксперимент, то сначала вам нужно разогреть горелку до меньшей температуры, затем прибавить к ней Dt, что и даст вам температуру плавления другого металла.

Во многих отраслях знаний буквой t обозначают время. Выражение «дельта t» в этих случаях также означает разность, но уже в показаниях часов. Засеките время и запишите результат. Подождите немного и снова посмотрите на часы. Допустим, в первый раз вы посмотрели на циферблат ровно в 14 часов, а второй — по прошествии 13 минут. Разность в этом случае составляет 13 минут. Это и есть Dt по условиям данной задачи.

На практике довольно часто приходится определять Dt без всяких вычислений. Например, во время соревнований по легкой атлетике арбитру важно знать, за какое время бегуны пробежали ту или иную дистанцию. При этом не особенно важно, во сколько начались состязания, объявлен старт раньше или позже указанного в афишах времени. В этом случае судья определяет только Dt. В начале забега он ставит секундомер на 0, а в конце – отмечает результат.

Обратите внимание

Определить Dt бывает необходимо и при сравнении движения разных объектов при прочих равных условиях. Этот способ тоже наиболее понятен, если представить себе спортсменов. Допустим, участников соревнований очень много, они все бегут одну и ту же дистанцию, но в разных забегах. Судьям нужно понять, кто окажется на каком месте в итоговой таблице. Для этого определяется лучший результат – в данном случае минимальный. С ним сравниваются все остальные. То есть каждый раз судьи находят Dt между временем первого и второго, второго и третьего спортсменов и т.д.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?