“Числа на координатной прямой”, так звучит тема заданий №7 на ОГЭ в 9 классе.
Сегодня предлагаю вам посмотреть подборку заданий в рамках дробных чисел. В следующих статьях обязательно посмотрим и другие виды чисел на координатной прямой.
Что нужно уметь для решения этого задания:
1) сравнивать дроби;
2) выделять целую часть в неправильных дробях;
3) приводить обыкновенные дроби к десятичному виду.
А вот и сегодняшние задания и их разбор.
№1
В этом задании достаточно выделить целую часть. Для этого поделим уголком 106 на 13. Помним, что неделимый остаток записываем в числитель, а знаменатель остается тот же.
Теперь сравниваем полученный результат с точками на прямой: точка должны быть больше 8, но достаточно близко к этому значению.
№2
По аналогии с предыдущим заданием выделим целую часть в каждой дроби. Обратим внимание, что значение в точке больше 7, но немного меньше, чем 8.
№3
В этом случае необходимо найти десятичные значения данных дробей. Для этого поделим числитель дроби на знаменатель в столбик. Проделаем это для каждого предложенного варианта. Значение верного варианта должно быть больше 0,5, но меньше 0,6
Продолжение следует…
Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность
(✿◠‿◠)

§ 1.1. Бесконечные десятичные дроби
Рациональные (в частности, целые) числа и их свойства считаются известными из школы. Рациональные числа можно сравнивать (т. е. для них введены понятия “равно”, “больше” и “меньше”), определены арифметические действия над рациональными числами – сложение, вычитание, умножение и деление.
Но рациональных чисел недостаточно даже для задач элемен-
тарной математики. Так, длина диагонали квадрата со стороной 1 p
равна 2, а это число иррациональное, т. е. не рациональное. Не является рациональным и число , выражающее длину окружности диаметра 1.
Напомним, что такое числовая прямая. На горизонтально расположенной прямой выбирают начальную точку O и единичный отрезок OE, отложенный вправо от точки O. Точке O ставится в соответствие число 0, точке E – число 1. Откладывая вправо от точки E шаг за шагом единичный отрезок, получают точки, соответствующие натуральным числам 2; 3; : : : , а откладывая единичный отрезок влево от точки O, – точки, соответствующие целым отрицательным числам 1; 2; : : : .
Затем строятся точки, соответствующие рациональным числам. При n = 2; 3; : : : отрезок OE делят на n равных частей и чтобы получить точку, соответствующую положительному рациональному числу m=n, вправо от точки O откладывают m раз отрезок длины 1=n. Точно также для отрицательных рациональных чисел находят соответствующие им точки слева от точки O.
Таким образом, каждому рациональному числу поставлена в соответствие точка на числовой прямой. Но при этом не каждой точке числовой прямой соответствует рациональное число. На-
пример, нет рационального числа, соответствующего точке, рас- p
положенной справа от O на расстоянии 2.
В этой главе рациональные числа будут пополнены до множества действительных чисел, в результате каждой точке числовой
7

|
8 |
Гл. 1. Действительные числа |
|||||
прямой будет соответствовать число, а каждому числу – точка на прямой.
Такое пополнение рациональных чисел можно осуществить разными способами. Мы сделаем это, используя бесконечные десятичные дроби. Такой способ был намечен в школе, но сейчас все рассуждения будут проведены заново.
Отметим, что определение действительных чисел как бесконечных десятичных дробей восходит к К. Вейерштрассу.
Построим десятичную дробь, соответствующую произвольной точке A числовой прямой.
Пусть точка A расположена справа от точки O и не отвечает натуральному числу. Найдём целые числа a0 и a0+1, между которыми лежит точка A. В качестве целой части десятичной дроби, соответствующей точке A, берём a0.
Далее отрезок между точками a0 и a0 + 1 делим на 10 равных частей и приписываем этим частям слева направо цифры от 0 до 9. Среди полученных промежутков длины 1/10 находим тот, внутри которого находится точка A (случай, когда A оказывается одной из точек деления, обсудим позднее) и в качестве первого десятичного знака искомой дроби берём цифру, приписанную этому промежутку. Продолжая этот процесс, получим (при условии, что A не оказывается точкой деления) бесконечную десятичную дробь, соответствующую точке A.
Рассмотрим теперь случай, когда точка A оказалась одной из точек деления. Пусть, например, A расположена как на рисунке:
|
0 |
1 |
2 |
9 |
||||||
|
a |
A |
a +1 |
|||||||
|
0 |
0 |
Точкам на промежутке, примыкающем к A справа, в качестве первого десятичного знака мы приписали цифру 2, а на промежутке, примыкающем слева, – цифру 1. По поводу самих точек деления нужно решить, к какому промежутку их относить: лежащему справа или лежащему слева. Если точки деления относить к
|
§ 1.1. Бесконечные десятичные дроби |
9 |
правым промежуткам, то для точки A на рисунке получим a0; 2, а все остальные десятичные знаки – ноли, т. е. получим a0; 2000 : : : . Если точки деления относить к левым промежуткам, то для точки A получим a0; 1, а все остальные десятичные знаки – девятки,
т.е. получим a0; 1999 : : : = a0; 1(9).
Взависимости от договоренности, относить точки деления к правым или к левым промежуткам, для точек, соответствующих натуральным числам, также получим две бесконечные десятичные дроби. У одной из них все десятичные знаки ноли, а у другой целая часть на единицу меньше, а все десятичные знаки – девятки.
Для точек числовой прямой слева от точки O пишем перед дробью знак минус, а затем подобным образом находим числа a0; a1; a2; : : : , определяющие соответствующую бесконечную десятичную дробь a0; a1a2 : : : .
Таким образом, для всех точек числовой прямой (кроме начальной точки O), которые оказываются точками деления, возможны две записи – с нолем в периоде (т. е. в виде целого числа или конечной десятичной дроби) или с девяткой в периоде. Для остальных точек бесконечная десятичная дробь определяется однозначно.
Чтобы каждой точке числовой прямой соответствовала единственная бесконечная десятичная дробь, уславливаются не различать получающиеся при указанном построении дроби с 0 и с 9 в периоде. Обычно в каждом рассуждении используют дроби только с нолем или только с девяткой в периоде.
Поставим обратную задачу – для заданной бесконечной десятичной дроби a0; a1a2 : : : найти соответствующую ей точку числовой прямой.
По знаку дроби и числу a0 находим два идущих подряд целых числа, между которыми должна располагаться искомая точка. Затем, разбив промежуток между этими точками на 10 равных частей, по числу a1 находим тот из полученных промежутков длины 1=10, которому должна принадлежать наша точка.
Продолжая шаг за шагом это построение, получим последовательность промежутков, каждый из которых содержится в предыдущем, а длина его в 10 раз меньше. Искомая точка должна принадлежать всем этим промежуткам.
|
10 |
Гл. 1. Действительные числа |
Но обязательно ли существует такая точка, мы сейчас не знаем. В дальнейшем на этот вопрос будет получен положительный ответ.
Всё сказанное о бесконечных десятичных дробях следует рассматривать как наводящие соображения к тому, чтобы назвать числами бесконечные десятичные дроби.
Определение. Действительными (вещественными) числами называют бесконечные десятичные дроби a0; a1a2 : : : , где выбран определённый знак: “+” или “ ”, a0 – натуральное число или нуль, а все десятичные знаки a1; a2; : : : – цифры от 0 до 9. При этом дробь a0; a1 : : : am(9), где am 6= 9, определяет то же число, что и дробь a0; a1 : : : am 1d000 : : : , у которой m-й десятичный знак d равен am + 1.
Действительные числа будем обозначать буквами и писать a = a0; a1a2 : : : , опуская обычно при этом знак +. Число 0 записывают как бесконечную дробь 0; 000 : : : , которую можно снабдить и знаком + и знаком , но как правило этой дроби знак не приписывают.
При записи чисел a; b; c; : : : в виде бесконечных десятичных дробей для обозначения десятичных знаков будем использовать эти же буквы с индексами:
a = a0; a1a2 : : : ; b = b0; b1b2 : : : ; c = c0; c1c2 : : : :
Для каждого числа a = a0; a1a2 : : : вводится число a, которое отличается от a только знаком, т. е. a := a0; a1a2 : : : . На числовой прямой точки, соответствующие числам a и a, расположены симметрично относительно начальной точки O.
Выясним, как соотносятся рациональные и действительные числа.
Рациональные числа представимы в виде дроби mn , где m – целое число, а n – натуральное.
Будем для определённости считать, что m > 0. Разделив m на n “уголком”, получим либо конечную десятичную дробь, которую можно записать в виде бесконечной дроби с 0 в периоде, либо бесконечную десятичную дробь, которая обязательно будет периодической.
В самом деле, остатками при делении на n могут быть только числа 1; 2; : : : ; n 1. Рассмотрим остатки, которые получаются при делении m на n после того, как все значащие цифры числа m
Соседние файлы в папке Лекции, матан
- #
- #
Дата: 13/02/2017
___________
Класс: 5
Предмет: математика
Урок №: 129
Тема урока: «Изображение
десятичных дробей на координатном луче.».
Цели
и задачи урока:
Образовательные:
– сформировать умение изображать десятичные дроби точками на
координатном луче, находить координаты точек, изображенных на координатном
луче;
Развивающие:
– продолжить работу
по развитию: 1) умений наблюдать, анализировать, сопоставлять, доказывать,
делать выводы; 2) математического и общего кругозора; 3) оценивать свою работу;
Воспитательные:
–
формировать умения высказывать свои мысли, слушать других, вести диалоги,
отстаивать свою точку зрения; формировать навыки самооценки.
Ход урока
I.
Организационный момент, приветствие, пожелания плодотворной
работы.
– Проверьте, всё
ли вы приготовили для урока.
II. Постановка целей урока.
Ребята
посмотрите внимательно на тему сегодняшнего урока. Как вы думаете, чем мы с
вами сегодня будем заниматься на уроке? Давайте вместе с вами попытаемся
сформулировать цели урока.
III.
Актуализация знаний. Все ученики пишут в тетрадях, один ученик
за закрытой доской. Учитель проверяет работу на доске, после чего все учащиеся
сравнивают и исправляют ошибки.
1) Математический диктант.
1.
Три целых одна десятая.
2.
Пять целых восемь десятых.
3.
Одна целая пять десятых.
4.
Ноль целых семьдесят сотых.
5.
Семь целых двадцать пять сотых.
6.
Ноль целых шестнадцать сотых.
7.
Три целых сто двадцать пять тысячных.
8.
Пять целых двенадцать сотых.
9.
Десять целых двадцать четыре сотых.
10.
Одна целая три десятых.
Ответы:
1. 3,1
2. 5,8
3. 1,5
4. 0,75
5. 7,25
6. 0,16
7. 3,125
8. 5,12
9. 10,24
10. 1,3
2) Устная работа
(1) Прочитайте десятичные дроби:
0,2
1,009 3,26 8,1 607,8 0,2345 0,001 3,07 27,27 0,24
100,001 3,08 3,89 71,007 5,0023
3)
Давайте
вспомним!
Чтобы
отметить точку на координатном луче, необходимо…
Какой
буквой отмечается точка на координатном луче?
Как
записывается координата точка?
3. Изучение нового материала.
Десятичные
дроби на координатном луче изображаются так же, как обыкновенные дроби.
(2)
1) Изобразим на координатном луче десятичную дробь 3,2.
Число
3,2 содержит 3 целых единицы и 2 десятых доли единицы. Сначала отметим на
координатном луче точку, соответствующую числу 3. Затем следующий единичный
отрезок разделим на десять равных частей и отсчитаем две такие части вправо от
числа 3. Так мы получим на координатном луче точку А, которая изображает
десятичную дробь 3,2. Расстояние от начала отсчета до точки А равно 3,2
единичного отрезка.(А=3,2).
Изобразим
на координатном луче десятичную дробь 3,2.

2) Изобразим на координатном луче десятичную дробь
0,56.

4. Закрепление изученного материала.
(3)
1. Дорога от Каратау до Коктала равна 10 км. Петя прошел 3 км. Какую часть
дороги он прошел?
![]()

1. На сколько равных
частей разделен весь путь? ( на 10 частей)
2. Чему будет равна одна
часть пути? (1/10 или 0,1)?
3. Чему будут равны три
части такого пути? (0,3)?
1. Какие числа
отмечены точками на координатной прямой.
(4) 2.
|
|
A(0,3); B(0,9); C(1,1); D(1,7). A(6,4); B(6,7); C(7,2); D(7,5); E(8,1). A(0,02); B(0,05); C(0,14); D(0,17). |
(5) 3.
На
координатной прямой некоторые точки обозначены буквами. Какая из точек
соответствует числу 34,8; 34,2; 34,6; 35,4; 35,8; 35,6?
|
E |
B |
D |
L |
N |
M |
![]()
(6) 4. Начертите
координатный луч. За единичный отрезок возьмите 5 клеток тетради. Найдите на
координатном луче точки А (0,9), В (1,2), С(3,0)
![]()
(7)
Работа с учебником: откройте в учебнике на стр.89, выполняем номер: № 1254
(задача на смекалку).

(8)
5. Физкультминутка, упражнение на внимание.
Посчитайте
фигуры так: «Первый треугольник, первый угол, первый круг, второй угол и т.д.»

Дифференцированная работа с учащимися (работа с
одаренными и слабоуспевающими учащимися).
6. Подведение итогов урока.
Ребята
что нового вы узнали сегодня на уроке?
Как
вы думаете, нам удалось достигнуть поставленных целей?
Рефлексия.
Как вы думаете
ребята, достиг ли мы поставленной цели?
-Что вы узнали на
уроке? – Чему вы научились на уроке?
Что понравилось
на уроке? Какие трудности возникли?
(9)7.
Домашнее задание:

2.
Придумайте сказку, которая должна начинаться так: В некотором царстве, в
некотором государстве, которое звалось “Государство чисел” жили-были
дроби: обыкновенные и десятичные
Опорный лист к уроку «Изображение десятичных
дробей на координатном луче».
1. Прочитайте десятичные дроби:
0,2
1,009 3,26 8,1 607,8 0,2345 0,001 3,07 27,27 0,24
100,001 3,08 3,89 71,007 5,0023
2. Изобразим на координатном луче десятичную
дробь 3,2.
а) Число 3,2 содержит 3 целых единицы и 2 десятых доли единицы.

б) Изобразим на координатном луче десятичную дробь 0,56.

3. Дорога от Каратау до Коктала равна 10
км. Петя прошел 3 км. Какую часть дороги он прошел?
![]()

1.
На сколько равных частей разделен весь путь?
2.
Чему будет равна одна часть пути?
3.
Чему будут равны три части такого пути?
4. Какие
числа отмечены точками на координатной прямой.

5. На координатной прямой некоторые точки обозначены
буквами. Какая из точек соответствует числу 34,8; 34,2; 34,6; 35,4; 35,8;
35,6?
![]()
6.
Начертите координатный луч. За единичный отрезок возьмите 5 клеток тетради.
Найдите на координатном луче точки А (0,9), В (1,2), С(3,0)

7. Работа с учебником: откройте
в учебнике на стр.89, выполняем номер: № 1254 (задача на смекалку).
8. Посчитайте фигуры так: «Первый
треугольник, первый угол, первый круг, второй угол и т.д.»

9. Домашнее задание:
1.
№ задания на доске
2.
Придумайте сказку, которая должна начинаться так: В некотором царстве, в
некотором государстве, которое звалось “Государство чисел” жили-были
дроби: обыкновенные и десятичные
Как выражать величины в виде дроби
Мар 27, 2021 | 4 класс |

В начальной школе мы постоянно чертим отрезки. И не всегда длина этих отрезков выражена в одной величине. Иногда длина отрезка выражена в виде дроби.
Например: в 1 дм – 10 см, т.е. 1 см – это десятая часть дм. Это можно записать так:
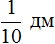
Это значит, что 1дм разделили на 10 равных частей и взяли 1 часть. Т.е. 1 см.

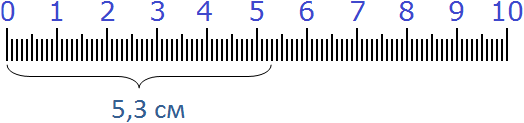
Если нужно начертить отрезок длиной 5 см и 3 мм.

5 см – уже есть, но надо еще 3 мм.
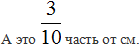
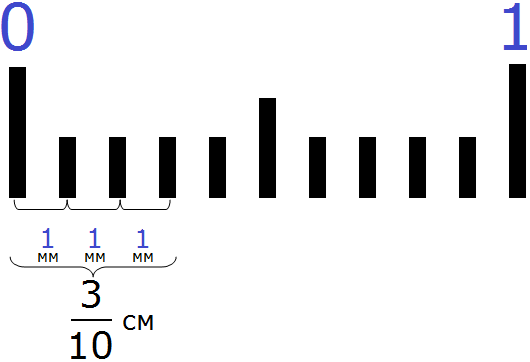
В итоге – у нас пять см и три десятых см: 5,3 см

Похожие статьи
Периодические десятичные дроби
10 февраля 2012
Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.
Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.
Периодическая десятичная дробь — это любая десятичная дробь, у которой:
- Значащая часть состоит из бесконечного количества цифр;
- Через определенные интервалы цифры в значащей части повторяются.
Набор повторяющихся цифр, из которых состоит значащая часть, называется периодической частью дроби, а количество цифр в этом наборе — периодом дроби. Остальной отрезок значащей части, который не повторяется, называется непериодической частью.
Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:
![]()
Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
![]()
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
![]()
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
![]()
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.
![]()
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».
Переход к периодической десятичной дроби
Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Возможны два варианта:
- В разложении присутствуют только множители 2 и 5. Эти дроби легко приводятся к десятичным — см. урок «Десятичные дроби». Такие нас не интересуют;
- В разложении присутствует что-то еще, кроме 2 и 5. В этом случае дробь непредставима в виде десятичной, зато из нее можно сделать периодическую десятичную дробь.
Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».
При этом будет происходить следующее:
- Сначала разделится целая часть, если она есть;
- Возможно, будет несколько чисел после десятичной точки;
- Через некоторое время цифры начнут повторяться.
Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.
Задача. Переведите обыкновенные дроби в периодические десятичные:
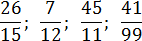
Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:
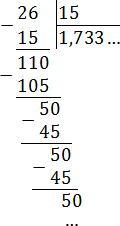
Как видим, остатки повторяются. Запишем дробь в «правильном» виде: 1,733 … = 1,7(3).
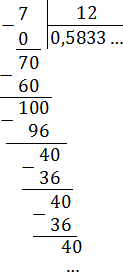
В итоге получается дробь: 0,5833 … = 0,58(3).
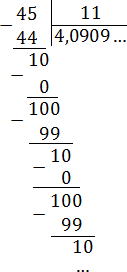
Записываем в нормальном виде: 4,0909 … = 4,(09).
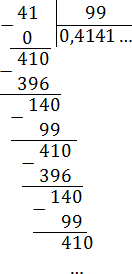
Получаем дробь: 0,4141 … = 0,(41).
Переход от периодической десятичной дроби к обыкновенной
Рассмотрим периодическую десятичную дробь X = abc(a1b1c1). Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:
- Найдите период дроби, т.е. подсчитайте, сколько цифр находится в периодической части. Пусть это будет число k;
- Найдите значение выражения X · 10k. Это равносильно сдвигу десятичной точки на полный период вправо — см. урок «Умножение и деление десятичных дробей»;
- Из полученного числа надо вычесть исходное выражение. При этом периодическая часть «сжигается», и остается обычная дробь;
- В полученном уравнении найти X. Все десятичные дроби переводим в обыкновенные.
Задача. Приведите к обыкновенной неправильной дроби числа:
- 9,(6);
- 32,(39);
- 0,30(5);
- 0,(2475).
Работаем с первой дробью: X = 9,(6) = 9,666 …
В скобках содержится лишь одна цифра, поэтому период k = 1. Далее умножаем эту дробь на 10k = 101 = 10. Имеем:
10X = 10 · 9,6666 … = 96,666 …
Вычитаем исходную дробь и решаем уравнение:
10X − X = 96,666 … − 9,666 … = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.
Теперь разберемся со второй дробью. Итак, X = 32,(39) = 32,393939 …
Период k = 2, поэтому умножаем все на 10k = 102 = 100:
100X = 100 · 32,393939 … = 3239,3939 …
Снова вычитаем исходную дробь и решаем уравнение:
100X − X = 3239,3939 … − 32,3939 … = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.
Приступаем к третьей дроби: X = 0,30(5) = 0,30555 … Схема та же самая, поэтому я просто приведу выкладки:
Период k = 1 ⇒ умножаем все на 10k = 101 = 10;
10X = 10 · 0,30555 … = 3,05555 …
10X − X = 3,0555 … − 0,305555 … = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.
Наконец, последняя дробь: X = 0,(2475) = 0,2475 2475 … Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:
k = 4 ⇒ 10k = 104 = 10 000;
10 000X = 10 000 · 0,2475 2475 = 2475,2475 …
10 000X − X = 2475,2475 … − 0,2475 2475 … = 2475;
9999X = 2475;
X = 2475 : 9999 = 25/101.
Смотрите также:
- Сравнение дробей

- Тест к уроку «Десятичные дроби» (2 вариант)

- Четырехугольная пирамида в задаче C2

- Как сдать ЕГЭ по математике

- Задача B5: площадь сектора

- Задача B4: тарифы на сотовую связь


