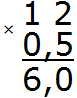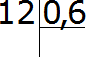В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Как найти десятичную дробь
Представление о дробях учащиеся школ получают еще на начальном этапе обучения. Не забывают про дроби и в старших классах, но вычислять их разрешается на калькуляторе, а потому забывается сам принцип возникновения дроби. На практике решать задачи при помощи основного свойства дробей проще, чем наугад набирать кнопки на калькуляторе

Вам понадобится
- – Учебник математики за 5ый класс.
Инструкция
Итак, давайте разберемся, с определением части от целого. Для этого сделайте рисунок квадрата или прямоугольника, лучше всего на листке в клеточку. Разделите квадрат по клеточкам, это будут доли, равные части одного целого.
Дроби бывают разными, например, обыкновенные – 1/2, 3/7, 1/4, смешанные – 1 ½, 2 ½
5 ¼ , десятичные дроби – 0,25, 0,5, 0,7.
Все дроби зависят от основного свойства дробей – сокращенные дроби, решайте задачи без калькулятора.
Дроби можно переводить из одного вида в другой. Например, дробь 25/100 можно записать как 0,25. Дробь можно сократить, получится ¼. Бывает, что десятичную дробь не нужно сокращать. Например, 0,3 так и останется 3/10 – эта дробь не сокращается. Но учтите, не все обыкновенные дроби можно представить в виде десятичных. Не найти десятичную дробь из 1/3, 6/7, 1/7, и таких не переводимых дробей много.
Попробуйте найти десятичную дробь из 3/20. Для начала разложите знаменатель этой дроби на простые множители, например 5*2*2. Запишите пример так: 3/20 = 3/20*5/5=15/100=0,15.
Таким образом, чтобы найти десятичную дробь, разложите знаменатель обыкновенной дроби на множители, уравняйте количество пятерок и двоек, выберите единственный множитель. Закрепите знание – найдите десятичную дробь из 3/50. Разложите знаменатель на множители 50=2*5*5, значит, двойку нужно представлять в виде дроби 2/2. 3/50*2/2=6/100=0,06.
Чтобы найти десятичную дробь из обыкновенной дроби разделите её числитель на знаменатель. Например, возьмите 5/8, разделите 5 на 8, получите 0,625. Десятичная дробь может быть бесконечной. Например, 18/7 в точную десятичную дробь превратить нельзя, потому что если 18 разделить на семь получится бесконечное число.
Видео по теме
Обратите внимание
Бесконечные дроби можно округлить, но это значение будет не точным.
Полезный совет
Если вы задумались над решением примера со смешанными дробями – (3/4+0,5)*(1 1/5–0,7). Найдите десятичные дроби из ¾ -0,75 и из 1 1/5 -1,2, решите пример, используя десятичные дроби.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Десятичные дроби имеют широкий спектр применения. Их применяют в экономике, медицине, машиностроении и во многих других отраслях. В данном уроке мы рассмотрим некоторые элементарные операции, которые могут пригодиться в будущем.
Сравнение десятичных дробей
Чтобы сравнить две десятичные дроби, нужно в обеих дробях сделать количество цифр после запятой одинаковым, приписáв к одной из них нули. Затем отбросить запятые в обеих дробях и сравнить получившиеся числа.
Например, сравним дроби 5,345 и 5,36. В первой дроби после запятой три цифры, а во второй только две. В конце второй дроби нужно приписать ещё один ноль, чтобы количество цифр после запятой в обеих дробях стало одинаковым.
Припишем в конце второй дроби ноль, тогда получим дроби 5,345 и 5,360. Теперь отбросим запятые в обеих дробях, получим 5345 и 5360. Ну и сравниваем их как обычные числа. 5345 меньше, чем 5360
5345 < 5360
Значит и дробь 5,345 меньше, чем дробь 5,36
5,345 < 5,36
Пример 2. Сравнить десятичные дроби 6,782 и 6,71
Сделаем количество цифр в обеих дробях одинаковым:
6,782
6,710
Отбросим запятые:
6782
6710
6782 больше, чем 6710
6782 > 6710
Значит и дробь 6,782 больше, чем дробь 6,71
6,782 > 6,71
Нахождение десятичной дроби от числа
В прошлых уроках мы находили обыкновенную дробь от числа. Для этого мы делили число на знаменатель дроби и полученный результат умножáли на числитель дроби.
Например, чтобы найти от числа 9, нужно число 9 разделить на знаменатель дроби
и полученный результат умножить на числитель этой же дроби
9 : 3 = 3
3 × 2 = 6
Значит от числа 9 составляет 6.
Но находить можно и десятичные дроби от числа. Нахождение десятичной дроби от числа намного проще. Чтобы найти десятичную дробь от числа, достаточно это число умножить на данную дробь.
Например, найдём 0,5 от числа 12. Чтобы найти 0,5 от числа 12, достаточно умножить 12 на 0,5
Получили ответ 6. Значит 0,5 от числа 12 составляет число 6.
Проверим правильно ли мы нашли 0,5 от числа 12. Сначала переведём десятичную дробь 0,5 в обыкновенную дробь. 0,5 это ноль целых и пять десятых. Ноль не пишем, а записываем сразу пять десятых:
Cделаем эту дробь более простой для нашей работы. Для этого сократим её на 5
Получили дробь . Теперь находим
от числа 12. Нетрудно догадаться, что
от числа 12 это число 6. Значит и десятичная дробь 0,5 от числа 12 была найдена правильно.
Пример 2. Найти 0,4 от одного метра
Один метр это 100 см. Чтобы найти 0,4 от 100 см, нужно 100 см умножить на 0,4. А чтобы умножить 100 см на 0,4 нужно в 0,4 перенести запятую вправо на две цифры:
100 × 0,4 = 40
Значит 0,4 от одного метра составляют 40 см.
Десятичную дробь также можно найти от десятичной дроби. Например, найдем 0,5 от 2,5. Для этого 2,5 нужно умножить на 0,5
2,5 × 0,5 = 1,25
Нахождение числа по десятичной дроби
В прошлых уроках мы находили число по обыкновенной дроби. Чтобы найти всё число по его дроби мы делили известное число на числитель дроби и полученный результат умножали на знаменатель дроби.
Например, если числа составляет 6, то для нахождения всего числа, нужно 6 разделить на 2 и полученный результат умножить на 4
6 : 2 = 3
3 × 4 = 12
Значит если всё число равно 12.
Находить число можно и по десятичной дроби. Нахождение числа по десятичной дроби намного проще. Чтобы найти число по десятичной дроби, достаточно это число разделить на данную дробь.
Пример 1. 0,6 всего числа составляет 12, найти всё число. Чтобы найти всё число, достаточно 12 разделить на 0,6.
Чтобы разделить 12 на 0,6 нужно в делимом и в делителе перенести запятую вправо на одну цифру. Тогда получим выражение 120 : 6. А это выражение вычисляется легко:
120 : 6 = 20
Значит, если 0,6 всего числа составляет 12, то всё число это 20.
Пример 2. Велосипедист проехал 3 км, что составляет 0,2 всего пути, который должен проехать велосипедист. Какой путь должен проехать велосипедист?
Если 0,2 всего пути составляют 3 км, то для того чтобы найти весь путь, нужно 3 разделить на 0,2. Чтобы разделить число 3 на 0,2 нужно в делимом и в делителе перенести запятую вправо на одну цифру. Тогда получим выражение 30 : 2. А это выражение вычисляется легко:
30 : 2 = 15
Значит весь путь, который должен проехать велосипедист составляет 15 км.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

В этом уроке мы узнаем, как найти дробь от числа, научимся находить проценты от чисел и применим эти навыки для решения задач.
Представим, что у нас есть 3-х килограммовый торт. Мы разрезали его на 8 частей и взяли три из них. В таких случаях хочется знать, сколько килограмм торта у нас есть.
Рассмотрим один из способов рассуждения в таких случаях.
Посчитаем, сколько весит каждый кусок торта.
(mathbf{3div8=frac{3}{8}})
То есть каждый кусок весит (mathbf{frac{3}{8}}) килограмма.
А так как у нас 3 куска торта, остается домножить вес одного куска на 3.
(mathbf{frac{3}{8}cdot3=frac{3cdot3}{8}=frac{9}{8}=1frac{1}{8}})
Так мы получили, что в трех кусках содержится (mathbf{1frac{1}{8}}) килограмма торта.
Эта информация доступна зарегистрированным пользователям
Сформулируем понятное правило: чтобы найти дробь от числа, надо перемножить число и эту дробь.
То есть, как и раньше, перемножаем числитель дроби и число, пишем в числитель результат умножения, а в знаменатель результата пишем знаменатель дроби.
Далее по необходимости сокращаем дробь или приводим к правильному виду из неправильного.
Дадим еще пару примеров.
Необходимо найти (mathbf{frac{2}{7}}) от 6-ти.
(mathbf{frac{2}{7}cdot6=frac{2cdot6}{7}=frac{12}{7}=1frac{5}{7}})
Или пусть дано задание найти (mathbf{frac{1}{3}}) от 9.
Здесь вы видите, что почти все заключается в сокращении.
(mathbf{frac{1}{3}cdot9=frac{1cdot9}{3}=frac{1cdot3}{1}=3})
Эта информация доступна зарегистрированным пользователям
Особенно часто можно слышать про проценты в контексте экономических высказываний: цены выросли на 15 %, доходы уменьшились на 5% и так далее.
Запись в виде 10 % нужно трактовать как 0.1
(mathbf{12%=0.12})
(mathbf{50%=0.5})
и так далее, то есть чтобы получить десятичную дробь, равную числу в процентах, надо поделить количество процентов на 100.
Таким образом, чтобы найти процент от числа, надо перевести проценты в десятичную дробь, а дальше воспользоваться правилом нахождения дроби от числа: умножить число на дробь.
Например, нужно найти 5 % от 200.
Первым действием преобразуем 5 % в десятичную дробь:
(mathbf{5%=5div100=0.05})
Вторым действием перемножаем найденную дробь и число:
(mathbf{0.05cdot200=10})
10 и будет являться 5 % от 200.
Рассмотрим еще пару примеров.
Найдите 20 % от 80:
(mathbf{20%=20div100=0.2})
(mathbf{0.2cdot80=16})
Также, если это кажется более удобным, можно перевести десятичную дробь в обычную и домножать на нее.
Найдем 50 % от 234:
(mathbf{50%=50div100=0.5=frac{1}{2}})
(mathbf{234cdotfrac{1}{2}=frac{234}{2}=frac{117cdot2}{2}=117})
И немного примеров уже без пояснений:
Эта информация доступна зарегистрированным пользователям
В начале урока мы уже разобрали пример с тортом, сейчас посмотрим на другие примеры.
Задача 1
Остап зарабатывает 40 000 рублей в месяц.
Из них (mathbf{frac{1}{4}}) это подработка.
Сколько рублей Остапу приносит подработка?
Решение:
В данной случае числом будет являться сумма заработка за месяц – 40 000
Ну а дробью, очевидно, будет (mathbf{frac{1}{4}}).
Тогда, чтобы найти прибыль от подработки, надо просто умножить дробь на число.
(mathbf{40000cdotfrac{1}{4}=frac{40000}{4}=10000})
Ответ: 10 000 рублей.
Теперь рассмотрим что-нибудь посложнее.
Задача 2
Порфирий живет в комнате площадью 18 квадратных метров.
3 кровати занимают (mathbf{frac{1}{3}}) площади комнаты.
Какую площадь занимает одна кровать?
Решение:
Сначала найдем, какую площадь занимают 3 кровати, затем разделим это число на 3, чтобы получить площадь одной кровати.
1) (mathbf{18cdotfrac{1}{3}=frac{18}{3}=6}) (квадратных метров) занимают 3 кровати
2) (mathbf{6div3=2}) (квадратных метра) занимает одна кровать
Ответ: 2 квадратных метра.
Теперь посмотрим, как в задачах применяются проценты.
Задача 3
Пересвет работает на заводе и производит 100 деталей в день.
Начальник Елисей пообещал Пересвету выдать премию, если он будет делать на 20% деталей больше.
Сколько деталей в день должен делать Пересвет, чтобы получить премию?
Решение:
Для начала надо понять, на сколько в количественном измерении больше деталей нужно выпустить Пересвету, чтобы получить премию.
Для этого домножим текущее количество деталей на процент или долю, учитывая, что 20% – это 20 частей из 100, или иначе 0,20, и получим искомую прибавку.
1) (mathbf{20%=20div100=0.2})
2) (mathbf{100cdot0.2=20}) (деталей)- то, насколько больше деталей нужно производить
Теперь, чтобы найти общее количество деталей, надо прибавить эту прибавку к тому, что Пересвет производит уже сейчас.
3) (mathbf{100+20=120}) (деталей) в день нужно производить для получения премии
Ответ: 120 деталей.
В некоторых задачах нужно несколько раз применять нахождение процентов от числа.
Задача 4
Глубина реки в начале мая была равна 10 метрам, к началу июня она обмелела на 10%, а к началу июля еще на 15% относительно показателей начала июня. Вычислите, какая глубина реки была в начале июля.
Решение:
Исходное число- 10 метров, дробь задана в виде процентов.
Первым действием нужно будет найти глубину реки в начале июня.
Здесь можно пойти двумя разными путями:
I. Посчитаем, на сколько метров опустился уровень воды, а затем вычтем это из исходных показателей.
0) (mathbf{10%=10div100=0.1})
1) (mathbf{10-10cdot0.1=10-1=9}) (метров)- глубина реки в начале июня
II. Можно вместо того, чтобы считать разницу и вычитать ее, посчитать сколько процентов останется и найти сразу именно эту часть от исходного числа.
Учитывая, что всего у нас 100%, да если глубина уменьшилась на 10%, то осталось 90%.
0) (mathbf{100-10=90}) (процентов) останется
1) (mathbf{90%=90div100=0.9})
2) (mathbf{10cdot0.9=9}) (метров)- глубина реки в начале июня
Как мы видим, эти два подхода дают одинаковый результат.
Поэтому вы можете выбирать любой из них в зависимости от задачи и ваших предпочтений.
Таким образом, мы посчитали глубину в начале июня. Теперь нужно понять, какая будет глубина в начале июля, когда глубина уменьшится еще на 15 процентов.
Используем в этом случае второй способ.
3) (mathbf{100-15=85}) (процентов) останется в июле от уровня июня
4) (mathbf{85%=85div100=0.85})
5) (mathbf{0.85cdot9=7.65}) (метров) составит глубина реки в начале июля
Ответ: 7.65 метра.
Эта информация доступна зарегистрированным пользователям
На этом занятии мы поработали с процентами.
Первые упоминания о них встречаются в Древнем Риме.
Например, Октавиан Август взимал налог в (mathbf{frac{1}{100}}) на товары с аукциона.
Но до XVI века, несмотря на обилие задач на проценты, связанных с торговлей, с процентами работали весьма неумело.
В 1584 году бельгийский ученый Симон Севин создал таблицы для подсчета процентов.
Также, по одной из версий, именно он и ввел слово «процент».
Если говорить про сам значок процента, то существуют разные версии его происхождения.
По одной из них он произошел от итальянского слова cento, которое писалось сокращенно как cto.
В какой-то момент буква «t» перешла в вид косой черты, и так знак дошел до нас.
Другой вариант также отсылает к Италии.
Букву «p» тогда писали не как сейчас, а еще и с горизонтальной чертой, проходящей под строкой.
Тогда при написании «р 100» 100 оказывалась над чертой. Постепенно р и 10 отошли, и осталась черта с ноликом.
Эта информация доступна зарегистрированным пользователям
Начнем с довольно простой, но в то же время интересной темы, в которой школьники зачастую делают ошибки – нахождение дроби от числа.
Что такое часть от целого? Если у нас есть некоторое значение и нам необходимо вычислить некоторую долю или дробь от этого значения. Например, зная вес пиццы, найти вес нескольких ее кусочков.
При этом нужная доля может быть выражена как в виде обыкновенной дроби, так и в виде десятичной дроби или процентов. Для нахождения процента от числа стоит предварительно перевести проценты в десятичную дробь, просто разделив на 100. Например, 28 % = 0,28.
Для того, чтобы найти, сколько весят x кусочков пиццы, порезанной на равные y кусков, нужно общий вес пиццы разделить на y и умножить на x. Допустим, пицца весит Q грамм. То есть нам необходимо найти вес x/y части пиццы.
Немного парадоксальная ситуация: нужно найти часть, а мы умножаем, а не делим. Но на самом деле никакого парадокса в этом нет, если вспомнить, что дробь, вернее, горизонтальная черта дроби – это деление.
Да и при умножении на десятичную дробь меньше 1 мы тоже получим значение меньшее, чем исходное.
Немного запутать может ситуация, когда целая часть выражена в виде обыкновенной или десятичной дроби. Не стоит обращать на это внимание. Алгоритм действий точно такой же.
Рассмотрим еще несколько примеров.
Для закрепления материала предлагаем несколько примеров для самостоятельного решения. Ответы размещайте в комментариях.
Надеемся, эта тема была вам интересна. Если что-то осталось непонятным, задавайте вопросы в комментариях.
Завтра разберемся, как найти число, если нам известна только его часть.
Ставим лайки, подписываемся, в комментариях пишем темы, которые вам хотелось бы разобрать, задаем вопросы.
До скорой встречи!