Профи
(633),
закрыт
12 лет назад
Удачник
Высший разум
(141080)
12 лет назад
В дополнительном коде записывают отрицательные числа, как дополнение положительного до 0.
Например, числу -1 соответствует 11111111, если речь идет об 1-байтовых числах.
Если к 11111111 прибавить 1, то получится 0, точно так же, как в десятичной системе -1 + 1 = 0
Чтобы перевести число из двоичного в доп. код, его нужно проинвертировать, а потом прибавить 1.
Но самое интересное – чтобы перевести из доп кода обратно в двоичный – надо сделать тоже самое!
Число в дополнительном коде: 11111000
Инвертируем: 00000111.
Прибавляем 1: 00001000, это число в двоичном коде.
Переводим в десятичный: 8. А поскольку оно было в доп. коде, значит оно отрицательное.
Ответ: -8.
Alex P
Профи
(556)
12 лет назад
11111000(2)=248(10)
Источник: голова и калькулятор
Источник: 11111000(2)=0*2^0+0*2^1+0*2^2+1*2^3+1*2^4+1*2^5+1*2^6+1*2^7=248(10)
Как записать десятичный эквивалент числа
так надо написать на 5








Здравствуйте! На рисунке изображён график функции у =f(х). Точки a, b, с, d и е задают на оси х четыре интервала. Помогите пользуясь ( Подробнее. )
2. В чем заключается принцип Ферма?
Плата за телефон составляет 350 рублей в месяц. В следующем году она увеличится на 12%. Сколько рублей придётся платить ежемесячно за ( Подробнее. )
Приведите примеры информации, которая в конкретной ситуа-
ции является:
актуальной (своевременной)/неактуальной ( Подробнее. )
От разведчика была получена шифрованная радиограмма, пере-
данная с использованием азбуки Морзе. При передаче радио-
граммы ( Подробнее. )
Ответ оставил Гуру
А) У нас есть число в двоичной системе счисления: 01001100. Над каждой цифрой напишем ее разряд (справа налево; разряд начинается с 0). Затем мы первую цифру данного нам числа должны перемножить на основание данного нам числа ( т.к 01001100 — двоичное число, то основание соответственно равно 2) в какой-то степени ( степень определяется разрядом цифры), затем нужно проделать это со всеми цифрами числа и сложить результаты(все это делается с право налево).
01001100(2) = 1*2^6 + 1*2^3 + 1*2^2 = 76(10) ( 0 можно опускать, так как при умножении на 0 всегда будет 0)
б) 00010101(2) = 1*2^4 + 1*2^2 + 1*2^0 = 21(10)
P.s Так как код прямой, то все разряды являются целом числом в двоичном коде. Самый крайний левый разряд определяет знак числа в десятичной системе счисления ( если 0, то +, если 1, то -)

Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Информатика.
Помогите записать десятичные эквиваленты чисел, не понимаю как это сделать.172 (8) (восьмёрка в учебнике записана маленьким шрифтом внизу) 2EA(16) 101010(2) 10,1(2) 243(6)
Лучший ответ:

Цифры записанные внизу указывают систему счисления
172₈ – число записано в восьмеричной системе счисления. Требуется перевести его в десятичной системе счисления.
172₈ = 1*8² 7*8¹ 2*8⁰ = 64 56 2 = 122₁₀ – т.е. 122 в десятичной
2ЕА₁₆ = 2*16² 14*16¹ 10*16⁰ = 512 224 10 = 746₁₀
101010₂ = 1*2⁵ 0*2⁴ 1*2³ 0*2² 1*2¹ 0*2⁰ = 32 0 8 0 2 0 = 42₁₀
10,1₂ = 1*2¹ 0*2⁰ 1*2⁻¹ = 2 0 1/2 = 2,5₁₀
243₆ = 2*6² 4*6¹ 3*6⁰ = 72 24 3 = 99₁₀
Двоичные числа и двоичная арифметика
Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа [1].
Вспомним нашу привычную десятичную систему счисления, в которой мы с детства производим все расчеты. Уже в начальной школе мы привыкли к терминам «единицы», «десятки», «сотни», «тысячи», «десятые», «сотые», «тысячные» и не задумываемся над тем, что они означают вес разряда, выраженный в виде числа, равного 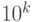 — целое число . Например, число 125, 46 можно представить в виде суммы:
— целое число . Например, число 125, 46 можно представить в виде суммы:
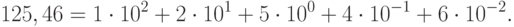
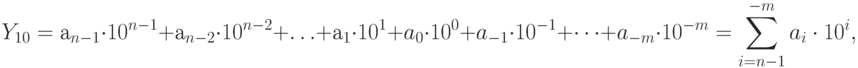 ( 11.1)
( 11.1)
где  — количество знаков в целой части числа,
— количество знаков в целой части числа,  — количество знаков в дробной части числа,
— количество знаков в дробной части числа,  -го разряда,
-го разряда,  -го разряда числа. Количество возможных вариантов значения коэффициента
-го разряда числа. Количество возможных вариантов значения коэффициента  , поскольку для записи чисел в ней используются десять знаков — арабские цифры «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9». Число
, поскольку для записи чисел в ней используются десять знаков — арабские цифры «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9». Число  является основанием системы счисления. Исторически сложилось, что десятичная система получила наибольшее распространение, хотя по этому принципу можно сделать аналогичную запись в любой другой системе счисления c любым другим основанием. В табл. 11.1 прослежива ется аналогия между позиционными системами счисления.
является основанием системы счисления. Исторически сложилось, что десятичная система получила наибольшее распространение, хотя по этому принципу можно сделать аналогичную запись в любой другой системе счисления c любым другим основанием. В табл. 11.1 прослежива ется аналогия между позиционными системами счисления.
Основание системы счисления — это число, равное количеству знаков, которые используются в этой системе для записи чисел.
Для числа в системе счисления с основанием  выражение (11.1) преобразуется к виду:
выражение (11.1) преобразуется к виду:
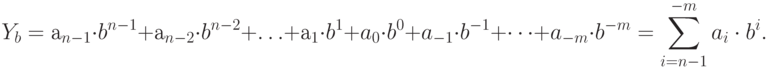 ( 11.2)
( 11.2)
| Название системы счисления | Основание системы счисления | Знаки, использующиеся для записи чисел |
|---|---|---|
| Двоичная | 2 | 0, 1 |
| Троичная | 3 | 0, 1, 2 |
| Четверичная | 4 | 0, 1, 2, 3 |
| … | … | … |
| Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| … | … | … |
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| … | … | … |
| Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
| … | … | … |
Таблица 11.1. Параметры позиционных систем счисления
С началом развития цифровой вычислительной техники большой интерес стала вызывать двоичная система, поскольку вычислительная машина любого поколения и любой степени сложности — это совокупность логических схем. Работа элементов этих схем основана на ключевом режиме работы транзистора, в котором он может быть только в двух состояниях, принимаемых за логический 0 и логическую 1.
Запись двоичного числа, как будет показано ниже, как правило, довольно длинна и громоздка, поэтому для более короткой записи двоичных чисел применяются восьмеричные и шестнадцатеричные числа. Выбор именно этих систем обусловлен тем, что их основания равны целой степени числа 2. Основание восьмеричной системы 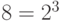 » в расчетную формулу (11.2) подставляется десятичное число
» в расчетную формулу (11.2) подставляется десятичное число  .
.
Из рассмотренных примеров видно, что общая формула (11.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную.
Перевод чисел из одной системы счисления в другую
Перевод из десятичной системы в любую другую. Перевод целых чисел
Целое десятичное число нужно поделить на основание новой системы счисления. Остаток от этого деления является самым младшим разрядом в новой записи числа. Результат деления вновь делится на основание. Остаток от этого деления будет следующим разрядом в новой записи числа, результат деления вновь делится на основание и т.д. до тех пор, пока в результате деления получится число, меньшее по величине, чем основание новой системы. Остаток этого последнего деления будет предпоследним разрядом в новой записи числа, а результат этого последнего деления — самым старшим разрядом в новой записи числа.
Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.
Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).
 в соответствии с таблицей 11.2.
в соответствии с таблицей 11.2.
Перевод из двоичной системы в шестнадцатеричную (восьмеричную)
Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.
Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).
Таблица 11.2. Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков
| Двоичная группа | Шестнадцатеричный знак | Десятичный эквивалент | Двоичная группа | Восьмеричный знак |
|---|---|---|---|---|
| 0000 | 0 | 0 | 000 | 0 |
| 0001 | 1 | 1 | 001 | 1 |
| 0010 | 2 | 2 | 010 | 2 |
| 0011 | 3 | 3 | 011 | 3 |
| 0100 | 4 | 4 | 100 | 4 |
| 0101 | 5 | 5 | 101 | 5 |
| 0110 | 6 | 6 | 110 | 6 |
| 0111 | 7 | 7 | 111 | 7 |
| 1000 | 8 | 8 | ||
| 1001 | 9 | 9 | ||
| 1010 | A | 10 | ||
| 1011 | B | 11 | ||
| 1100 | C | 12 | ||
| 1101 | D | 13 | ||
| 1110 | E | 14 | ||
| 1111 | F | 15 |
- перевод в шестнадцатеричную систему:
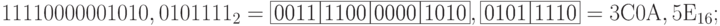
Десятичный эквивалент
Cтраница 1
Десятичный эквивалент такого числа всегда положителен.
[1]
Десятичные эквиваленты разрядов искомого числа находим, пользуясь примером на стр.
[2]
Десятичными эквивалентами чисел А и В являются 46202483 и 24600224 соответственно. Предположим также, что импульсы в машине следуют один за другим через / мксек, так что двоичные цифры слова передаются одна за другой каждую микросекунду. По мере того как оба аргумента разряд за разрядом продвигаются в сумматор, разряд за разрядом формируется и результат; частичные результаты помещаются в аккумуляторе перед ( в да ином случае левее) частично использованного первого аргумента, как это показано на рисунках.
[3]
Как только десятичный эквивалент кода на выходе одного из счетчиков станет равным 9, на выходе этого логического устройства формируется низкий уровень, блокирующий тактовые генераторы ГТ1, ГТ2 и ГТЗ. В дальнейшем изменений положения включенного светодиода в линейках Н ] и Н2 не происходит.
[4]
Когда десятичный эквивалент дополнительного кода отрицательной величины с фиксированной точкой определен с помощью таблицы преобразования, его следует вычесть из максимальной отрицательной величины с фиксированной точкой, представленной полем длиной в полуслово.
[5]
Аналогично определяется десятичный эквивалент сомножителя У.
[6]
N – десятичный эквивалент двоичного кода, линейные преобразователи различаются характеристиками ее равномерности.
[7]
С учетом десятичного эквивалента ( веса) каждого разряда, приведенного в табл. 4.3, перевод двоичных чисел в привычную нам десятичную систему счисления не представляет большого труда.
[9]
Так как для десятичного эквивалента числа, состоящего из 31 бита, отводится 15 десятичных цифр, переполнение не может возникнуть.
[10]
Параметр л заменяется десятичным эквивалентом этого бита. Если значения всех входов Рп есть степени с основанием 2, n может быть заменен двоичным порядком.
[12]
Параметр л заменяется десятичным эквивалентом этого бита. Если значения всех входов Рп есть степени с основанием 2, п может быть заменен двоичным порядком.
[14]
Страницы:
1
2
3
4
Найдите десятичные эквиваленты чисел по их прямым кодам

Рабочая тетрадь по Информатике 8 класс Босова
Задание 64. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком.
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Ответ: +85
Число положительное, так как знак-разряд 0.
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
Ответ: -120
Число отрицательное, так как знак-разряд 1.
<- Предыдущее задание Следующее задание ->
Вход
Быстрая регистрация
Если вы у нас впервые:
О проекте
FAQ
ГЛАВНАЯ
ВОПРОСЫ
ТЭГИ
СООБЩЕСТВО
НАГРАДЫ
ЗАДАТЬ ВОПРОС
|
0
Magic Fairy Tale 5 лет назад
Найдите десятичные эквиваленты чисел по их прямым кодам 01001100 и 00010101. Как решать? тэги: 01001100 и 00010101, десятичные эквиваленты чисел, как найти, как решать, по прямым кодам категория: образование ответить комментировать
в избранное
бонус 1 ответ: старые выше новые выше по рейтингу 0
natkru 5 лет назад 00010101 = 0∙2^7+0∙2^6+0∙2^5+1∙2^4+0∙2^3+1∙2^2+0∙2^1+1∙2^0 = 0+0+0+16+0+4+0+1 = 21 в десятеричной 01001100 = 0∙2^7+1∙2^6+0∙2^5+0∙2^4+1∙2^3+1∙2^2+0∙2^1+0∙2^0 = 0+64+0+0+8+4+0+0 = 76 в десятеричной комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Смотрите также: Как решить уравнение – найти x и угол y , см. рисунок? Как решить задачу о червяке и цилиндре с отверстиями? На сколько нужно больше топлива для полета на Луну по прямой, без …? Числительное как глагол. Какие есть примеры и предложения? Оплата по QR-коду это оплата, покупка или перевод? Вернуть деньги с чека по QR-коду Это реклама развод или правда? Я не поняла про вход по QR-код в Москве, что делать, еще раз прививаться? Сколько и кому Украина должна заплатить по долгам в 2017 году? Погода в Киеве и Киевской области с 19 по 25 мая 2014. Какая будет погода? Погода в Киеве и Киевской области с 12 по 18 мая 2014. Какая будет погода? |
|
Есть интересный вопрос? Задайте его нашему сообществу, у нас наверняка найдется ответ! |
Делитесь опытом и знаниями, зарабатывайте награды и репутацию, заводите новых интересных друзей! |
Задавайте интересные вопросы, давайте качественные ответы и зарабатывайте деньги. Подробнее.. |
Статистика проекта за месяц
Новых пользователей: 4390
Создано вопросов: 16462
Написано ответов: 38260
Начислено баллов репутации: 910082
ВОПРОСЫ
Свежие
С бонусами
Без ответов
Задать вопрос
Пульс проекта
СООБЩЕСТВО
Авторы
Награды
Тэги
Наши модераторы
Сейчас online
НАШ ПРОЕКТ
О проекте
Правила
Как заработать?
Партнерская программа
РЕСУРСЫ
Наш блог
Обратная связь
FAQ
Помогите нам стать лучше
Telegram-канал
