Как найти det a для 3 - Сайт, где вы сможете решить свои вопросы

Определитель матрицы: алгоритм и примеры вычисления определителя матрицы

Перед тем как находить и считать определитель, дадим определение определителю матрицы.

Определение 1

Что такое определитель матрицы или детерминант матрицы? Определитель матрицы — это некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.

|А|, ∆, det A – символы, которыми обозначают определитель матрицы.

Как найти определитель матрицы? Вычислить определитель или найти определитель можно с помощью разных способов (в том числе онлайн и при помощи калькулятора). Конкретный способ поиска и того, как решать, выбирают в зависимости от порядка матрицы.

Пример 1

Определитель матрицы второго порядка можно вычислять по формуле:

А=1-231.

Решение матрицы:

det A=1-231=1×1-3×(-2)=1+6=7

Определитель матрицы 3-го порядка: правило треугольника

Нахождение определителя матрицы 3-го порядка осуществляется по одному из правил:

он может считаться по правилу треугольника;
расчет также проводится по правилу Саррюса.

Как найти определитель матрицы третьего порядка по методу треугольника (определитель матрицы 3×3)?

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 2

А=13402115-1

Решение:

det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12

Правило Саррюса

Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:

дописать слева от определителя два первых столбца;
перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 3

А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3

Методы разложения по элементам строки и столбца

Чтобы вычислить определитель матрицы четвертого порядка, можно воспользоваться одним из 2-х способов:

разложением по элементам строки;
разложением по элементам столбца.

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.

Пример 4

Разложение матрицы по элементам строки:

det A=ai1×Ai1+ai2×Ai2+…+аin×Аin

Разложение матрицы по элементам столбца:

det A=а1i×А1i+а2i×А2i+…+аni×Аni

Замечание

Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.

Пример 5

А=01-132100-24513210

Решение:

раскладываем по 2-ой строке:

А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310

раскладываем по 4-му столбцу:

А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321

Свойства определителя

Свойства определителя:

если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
если поменять местами строки и столбцы, то знак поменяется на противоположный;
определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.

Замечание

В рамках темы советуем обратиться к модулю определителя.

Пример 6

А=134021005

Решение:

det А=134021005=1×5×2=10

Замечание

Матричныый определитель, который содержит нулевой столбец, равный нулю (представляет собой минор).

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Загрузить PDF

Определители матриц часто используются в вычислениях, в линейной алгебре и аналитической геометрии. Вне академического мира определители матриц постоянно требуются инженерам и программистам, в особенности тем, кто работает с компьютерной графикой. Если вы уже знаете, как найти определитель матрицы размерностью 2×2, то из инструментов для нахождения определителя матрицы 3×3 вам будут необходимы только сложение, вычитание и умножение.

1
Запишите матрицу размерностью 3 x 3. Запишем матрицу размерностью 3 x 3, которую обозначим M, и найдем ее определитель |M|. Далее приводится общая форма записи матрицы, которую мы будем использовать, и матрица для нашего примера:
- $M={begin{pmatrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{{23}}\a_{{31}}&a_{{32}}&a_{{33}}end{pmatrix}}={begin{pmatrix}1&5&3\2&4&7\4&6&2end{pmatrix}}$
2
Выберите строку или столбец матрицы. Эта строка (или столбец) будет опорной. Результат будет одинаков, независимо от того, какую строку или какой столбец вы выберете. В данном примере давайте возьмем первую строку. Чуть позже вы найдете несколько советов касательно того, как выбирать строку или столбец, чтобы упростить вычисления.
- Давайте выберем первую строку матрицы M в нашем примере. Обведите числа 1 5 3. В общей форме обведите a₁₁ a₁₂ a₁₃.
3
Зачеркните строку или столбец с первым элементом. Обратитесь к опорной строке (или к опорному столбцу) и выберите первый элемент. Проведите горизонтальную и вертикальную черту через этот элемент, вычеркнув таким образом столбец и строку с этим элементом. Должно остаться четыре числа. Будем считать эти элементы новой матрицей размерностью 2 x 2.
- В нашем примере, опорной строкой будет 1 5 3. Первый элемент находится на пересечении первого столбца и первой строки. Вычеркните строку и столбец с этим элементом, то есть первую сроку и первый столбец. Запишите оставшиеся элементы в виде матрицы 2 x 2:
- ~~1 5 3~~
- 2 4 7
- 4 6 2
4
Найдите определитель матрицы 2 x 2. Запомните, что определитель матрицы ${begin{pmatrix}a&b\c&dend{pmatrix}}$ вычисляется как ad – bc.^[1] Опираясь на это, вы можете вычислить определитель полученной матрицы 2 x 2, которую, если хотите, можете обозначить как X. Умножьте два числа матрицы X, соединенных по диагонали слева направо (то есть так: ). Затем вычтите результат умножения двух других чисел по диагонали справа налево (то есть так: / ). Используйте эту формулу, чтобы вычислить определитель матрицы, которую вы только что получили.
- В нашем примере определитель матрицы ${begin{pmatrix}4&7\6&2end{pmatrix}}$ = 4*2 – 7*6 = -34.
- Этот определитель называется минором элемента, который мы выбрали в нашей первоначальной матрице.^[2] Другими словами, мы только что нашли минор a₁₁.
5
Умножьте полученный ответ на выбранный элемент матрицы M. Вспомните, какой элемент из опорной строки (или столбца) мы использовали, когда вычеркивали другие элементы строки и столбца, чтобы получить новую матрицу. Умножьте этот элемент на полученный минор (определитель матрицы 2×2, которую мы обозначили X).
- В нашем примере мы выбирали элемент a₁₁, который равнялся 1. Умножим его на -34 (определитель матрицы 2×2), и у нас получится 1*-34 = -34.
6
Определите знак полученного результата. Далее вам понадобится умножить полученный результат на 1, либо на -1, чтобы получить алгебраическое дополнение (кофактор) выбранного элемента. Знак кофактора будет зависеть от того, в каком месте матрицы 3×3 стоит элемент. Запомните эту простую схему знаков, чтобы знать знак кофактора:
- + – +
- – + –
- + – +
- Поскольку мы работали с элементом a₁₁, для которого стоит знак +, то мы будем умножать полученное значение на +1 (то есть оставим его как есть). Алгебраическое дополнение нашего элемента будет равно -34.
- Вы также можете найти знак алгебраического дополнения по формуле (-1)^{i+j, где i и j – номер столбца и строки выбранного элемента соответственно.^[3]}
7

Повторите все вышеописанные действия со вторым элементом опорной строки (или столбца). Вернитесь к исходной матрице размерностью 3×3 и строке, которую мы обвели в самом начале вычислений. Повторите все действия с этим элементом:
8
Повторите с третьим элементом. Далее вам понадобится найти еще одно алгебраическое дополнение. Вычислите его для последнего элемента опорной строки или опорного столбца. Далее приводится краткое описание того, как вычисляется алгебраическое дополнение для a₁₃ в нашем примере:
- Зачеркните первую строку и третий столбец, чтобы получить матрицу ${begin{pmatrix}2&4\4&6end{pmatrix}}$
- Ее определитель равен 2*6 – 4*4 = -4.
- Умножьте результат на элемент a₁₃: -4 * 3 = -12.
- Элемент a₁₃ имеет знак + в приведенной выше таблице, поэтому ответ будет -12.
9
Сложите полученные результаты. Это последний шаг. Вам необходимо сложить полученные алгебраические дополнения элементов опорной строки (или опорного столбца). Сложите их вместе, и вы получите значение определителя матрицы 3×3.
- В нашем примере определитель равен -34 + 120 + -12 = 74.
Реклама

1
Выбирайте в качестве опорной строки (или столбца) ту, что имеет больше нулей. Помните, что в качестве опорной вы можете выбрать любую строку или столбец. Выбор опорной строки или столбца не влияет на результат. Если вы выберете строку с наибольшим количеством нулей, вам придется выполнять меньше вычислений, поскольку вам будет необходимо вычислить алгебраические дополнения только для ненулевых элементов. Вот почему:
- Допустим, вы выбрали 2 строку с элементами a₂₁, a₂₂, and a₂₃. Чтобы найти определитель, вам будет необходимо найти определители трех различных матриц размерностью 2×2. Давайте назовем их A₂₁, A₂₂, and A₂₃.
- То есть определитель матрицы 3×3 равен a₂₁|A₂₁| – a₂₂|A₂₂| + a₂₃|A₂₃|.
- Если оба элемента a₂₂ и a₂₃ равны 0, то наша формула становится намного короче a₂₁|A₂₁| – 0*|A₂₂| + 0*|A₂₃| = a₂₁|A₂₁| – 0 + 0 = a₂₁|A₂₁|. То есть необходимо вычислить только алгебраическое дополнение одного элемента.
2

Используйте сложение строк, чтобы упростить матрицу. Если вы возьмете одну строку и прибавите к ней другую, то определитель матрицы не изменится. То же самое верно и для столбцов. Подобные действия можно выполнять несколько раз, кроме того, вы можете умножать значения строки на постоянную (перед сложением) для того, чтобы получить как можно больше нулей. Подобные действия могут сэкономить массу времени.
3
Помните, что вычислять определитель треугольных матриц намного проще. Определитель треугольных матриц вычисляется как произведение элементов на главной диагонали, от a₁₁ в верхнем левом углу до a₃₃ в нижнем правом углу. Речь в данном случае идет о треугольных матрицах размерностью 3×3. Треугольные матрицы могут быть следующих видов, в зависимости от расположения ненулевых значений:^[4]
- Верхняя треугольная матрица: Все ненулевые элементы находятся на главной диагонали и выше нее. Все элементы ниже главной диагонали равны нулю.
- Нижняя треугольная матрица: Все ненулевые элементы находятся ниже главной диагонали и на ней.
- Диагональная матрица: Все ненулевые элементы находятся на главной диагонали. Является частным случаем вышеописанных матриц.
Реклама

Советы

Описанный метод распространяется на квадратные матрицы любого ранга. Например, если вы используете его для матрицы 4×4, то после «вычеркивания» будут оставаться матрицы 3×3, для которых определитель будет вычисляться вышеупомянутым способом. Будьте готовы к тому, что вычислять определитель для матриц таких размерностей вручную — очень трудоемкая задача!
Если все элементы строки или столбца равны 0, то определитель матрицы тоже равен 0.

Об этой статье

Эту страницу просматривали 119 212 раз.

Была ли эта статья полезной?

Источник

Определитель матрицы.

Навигация по странице:

Определение определителя матрицы
Свойства определителя матрицы
Методы вычисления определителя матрицы
- Определитель матрицы 1×1
- Определитель матрицы 2×2
- Определитель матрицы 3×3
  - Правило треугольника для вычисления определителя матрицы 3-тего порядка
  - Правило Саррюса для вычисления определителя матрицы 3-тего порядка
- Определитель матрицы произвольного размера
  - Разложение определителя по строке или столбцу
  - Приведение определителя к треугольному виду
  - Теорема Лапласа

Определитель матрицы или детерминант матрицы – это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.

Определение.

Определителем матрицы n×n будет число:

det(A) =	Σ	(-1)^{N(α₁,α₂,…,α_n)}·a_α₁1·a_α₂2·…·a_{α_nn}
	(α₁,α₂,…,α_n)

где (α₁,α₂,…,α_n) – перестановка чисел от 1 до n, N(α₁,α₂,…,α_n) – число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n.

Обозначение

Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).

Свойства определителя матрицы

Определитель матрицы с двумя равными строками (столбцами) равен нулю.
Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
При транспонировании значение определителя матрицы не меняется:

det(A) = det(A^T)
Определитель обратной матрицы:

det(A^-1) = det(A)^-1
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
Общий множитель в строке (столбце) можно выносить за знак определителя:

a₁₁a₁₂…a_1n
a₂₁a₂₂…a_2n
….
k·a_i1k·a_i2…k·a_in
….
a_n1a_n2…a_nn

=
k·
a₁₁a₁₂…a_1n
a₂₁a₂₂…a_2n
….
a_i1a_i2…a_in
….
a_n1a_n2…a_nn
Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени:

B = k·A => det(B) = kⁿ·det(A)

где A матрица n×n, k – число.
Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:

a₁₁a₁₂…a_1n
a₂₁a₂₂…a_2n
….
b_i1 + c_i1b_i2 + c_i2…b_in + c_in
….
a_n1a_n2…a_nn

=

a₁₁a₁₂…a_1n
a₂₁a₂₂…a_2n
….
b_i1b_i2…b_in
….
a_n1a_n2…a_nn

+

a₁₁a₁₂…a_1n
a₂₁a₂₂…a_2n
….
c_i1c_i2…c_in
….
a_n1a_n2…a_nn
Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
Определитель произведения матриц равен произведению определителей этих матриц:

det(A·B) = det(A)·det(B)

Методы вычисления определителя матрицы

Вычисление определителя матрицы 1×1

Правило:

Для матрицы первого порядка значение определителя равно значению элемента этой матрицы:

∆ = |a₁₁| = a₁₁

Вычисление определителя матрицы 2×2

Правило:

Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:

∆ =

a₁₁	a₁₂
a₂₁	a₂₂

= a₁₁·a₂₂ – a₁₂·a₂₁

Пример 1.

Найти определитель матрицы A

Решение:

det(A) =

5	7
-4	1

= 5·1 – 7·(-4) = 5 + 28 = 33

Вычисление определителя матрицы 3×3

Правило треугольника для вычисления определителя матрицы 3-тего порядка

Правило:

Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

∆ =

a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

=
a₁₁·a₂₂·a₃₃ +
a₁₂·a₂₃·a₃₁ +
a₁₃·a₂₁·a₃₂ –
a₁₃·a₂₂·a₃₁ –
a₁₁·a₂₃·a₃₂ –
a₁₂·a₂₁·a₃₃

Правило Саррюса для вычисления определителя матрицы 3-тего порядка

Правило:

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком “минус”:

∆ =

a₁₁	a₁₂	a₁₃	a₁₁	a₁₂
a₂₁	a₂₂	a₂₃	a₂₁	a₂₂
a₃₁	a₃₂	a₃₃	a₃₁	a₃₂

=
a₁₁·a₂₂·a₃₃ +
a₁₂·a₂₃·a₃₁ +
a₁₃·a₂₁·a₃₂ –
a₁₃·a₂₂·a₃₁ –
a₁₁·a₂₃·a₃₂ –
a₁₂·a₂₁·a₃₃

Пример 2.

Найти определитель матрицы A =

571
-410
203

Решение:

det(A) =

571
-410
203

=
5·1·3 + 7·0·2 + 1·(-4)·0 –
1·1·2 – 5·0·0 – 7·(-4)·3 = 15 + 0 + 0 – 2 – 0 + 84 = 97

Вычисление определителя матрицы произвольного размера

Разложение определителя по строке или столбцу

Правило:

Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:

	n
det(A) =	Σ	a_ij·A_ij	– разложение по i-той строке
	j = 1

Правило:

Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:

	n
det(A) =	Σ	a_ij·A_ij	– разложение по j-тому столбцу
	i = 1

При разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.

Пример 3.

Найти определитель матрицы A

Решение: Вычислим определитель матрицы разложив его по первому столбцу:

det(A) =

2	4	1
0	2	1
2	1	1

= 2·(-1)¹⁺¹·

21
11

+ 0·(-1)²⁺¹·

41
11

+ 2·(-1)³⁺¹·

41
21

= 2·(2·1 – 1·1) + 2·(4·1 – 2·1) = 2·(2 – 1) + 2·(4 – 2) = 2·1 + 2·2 = 2 + 4 = 6

Пример 4.

Найти определитель матрицы A

Решение: Вычислим определитель матрицы, разложив его по второй строке (в ней больше всего нулей):

det(A) =

2411
0200
2113
4023

– 0·

411
113
023

+ 2·

211
213
423

– 0·

241
213
403

+ 0·

241
211
402
=

= 2·(2·1·3 + 1·3·4 + 1·2·2 – 1·1·4 – 2·3·2 – 1·2·3) = 2·(6 +12 + 4 – 4 – 12 – 6) = 2·0 = 0

Приведение определителя к треугольному виду

Правило:

Используя свойства определителя для элементарных преобразований над строками и столбцами 8 – 11, определитель приводится к треугольному виду, и тогда его значение будет равно произведению элементов стоящих на главной диагонали.

Пример 5.

Найти определитель матрицы A приведением его к треугольному виду

Решение:

det(A) =

2411
0210
2113
4023

Сначала получим нули в первом столбце под главной диагональю. Для этого отнимем от 3-тей строки 1-ую строку, а от 4-той строки 1-ую строку, умноженную на 2:

det(A) =

2411
0210
2 – 21 – 41 – 13 – 1
4 – 2·20 – 4·22 – 1·23 – 1·2

2411
0210
0-302
0-801

Получим нули во втором столбце под главной диагональю. Для этого поменяем местами 2-ой и 3-тий столбцы (при этом детерминант сменит знак на противоположный):

det(A) = –

2141
0120
00-32
00-81

Получим нули в третьем столбце под главной диагональю. Для этого к 3-ему столбцу добавим 4-тий столбец, умноженный на 8:

det(A) = –

214 + 1·81
012 + 0·80
00-3 + 2·82
00-8 + 1·81

=
–
21121
0120
00132
0001
= -2·1·13·1 = -26

Теорема Лапласа

Теорема:

Пусть ∆ – определитель n-ого порядка. Выберем в нем произвольные k строк (столбцов), причем k < n. Тогда сумма произведений всех миноров k-ого порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.

Источник

Мы уже знакомы с понятием определителя матрицы. Также мы рассмотрели правила вычисления детерминантов (определителей) первого и второго порядка. Познакомимся с различными вариантами нахождения определителей третьего порядка.

Вычисление определителей по правилу треугольника

Схематически раскрытие определителя по этому правилу выглядит так:

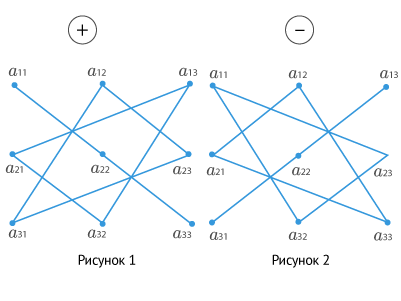
Согласно рисункам №1 и №2 мы перемножаем элементы, соединенные прямыми. Произведения элементов будут иметь определенные знаки: для рисунка 1 — «+», для рисунка 2 — «-».

Произведения, которые берутся со знаком «+»	Произведения, которые берутся со знаком «-»
a11⋅a22⋅a33a_{11} cdot a_{22} cdot a_{33}	a13⋅a22⋅a31a_{13}cdot a_{22}cdot a_{31}
a12⋅a23⋅a31a_{12} cdot a_{23} cdot a_{31}	a12⋅a33⋅a21a_{12}cdot a_{33}cdot a_{21}
a13⋅a32⋅a21a_{13} cdot a_{32} cdot a_{21}	a11⋅a23⋅a32a_{11}cdot a_{23}cdot a_{32}

На рисунке 1 мы видим равнобедренные треугольники с основаниями, параллельными главной диагонали; на рисунке 2 — равнобедренные треугольники с основаниями, параллельными второй (побочной) диагонали. Поэтому данное правило имеет такое название.

Определитель может быть вычислен по формуле:

∣a11a12a13a21a22a23a31a32a33∣=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=

=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a32⋅a21−a13⋅a22⋅a31−a12⋅a33⋅a21−a11⋅a23⋅a32=a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{13}cdot a_{32}cdot a_{21}-a_{13}cdot a_{22}cdot a_{31}-a_{12}cdot a_{33}cdot a_{21}-a_{11}cdot a_{23}cdot a_{32}.

Примеры

Рассмотрим примеры нахождения определителя по правилу треугольника.

Пример 1

Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по правилу треугольника.

По правилу треугольника определитель третьего порядка равен:

∣925148637∣=9⋅4⋅7+2⋅8⋅6+5⋅3⋅1−5⋅4⋅6−2⋅7⋅1−9⋅8⋅3=begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}=9cdot4cdot7+2cdot8cdot6+5cdot3cdot1-5cdot4cdot6-2cdot7cdot1-9cdot8cdot3=

=252+96+15−120−14−216=13=252+96+15-120-14-216=13.

Пример 2

Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по правилу треугольника.

Искомый определитель третьего порядка равен:

∣21−46−3510−1∣=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}=

=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅0⋅6−(−4)⋅(−3)⋅1−1⋅(−1)⋅6−2⋅5⋅0=6+5−12+6=5=2cdot(-3)cdot(-1)+1cdot5cdot1+(-4)cdot0cdot6-(-4)cdot(-3)cdot1-1cdot(-1)cdot6-2cdot5cdot0=6+5-12+6=5.

При вычислении определителей таким способом можно легко совершить ошибку из-за невнимательности. Чтобы избежать таких ошибок существует второй способ, называемый правилом Саррюса, или способом «параллельных полосок».

Вычисление определителей по правилу Саррюса

Правило Саррюса также именуют способом присоединения двух строк/столбцов или правилом параллельных полосок.

Основная идея этого правила состоит в приписывании первого и второго столбца справа от определителя.

Вычисления будем производить по следующей схеме:

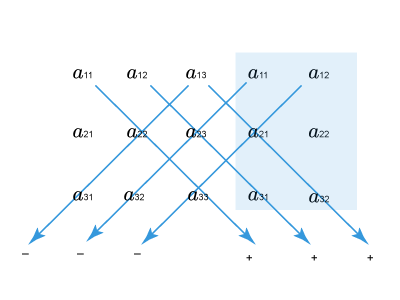
Перемножаем элементы, соединенные прямыми. Данные произведения берем со знаком «+», если диагональ, на которой они стоят, является главной или параллельной ей; со знаком «-», если она является второй (побочной) или параллельной ей.

Произведения, которые берутся со знаком «+»	Произведения, которые берутся со знаком «-»
a11⋅a22⋅a33a_{11} cdot a_{22} cdot a_{33}	a13⋅a22⋅a31a_{13}cdot a_{22}cdot a_{31}
a12⋅a23⋅a31a_{12} cdot a_{23} cdot a_{31}	a11⋅a23⋅a32a_{11}cdot a_{23}cdot a_{32}
a13⋅a21⋅a32a_{13} cdot a_{21} cdot a_{32}	a12⋅a21⋅a33a_{12}cdot a_{21}cdot a_{33}

В общем виде вычисление по правилу Саррюса можно записать следующим образом:

∣a11a12a13a21a22a23a31a32a33∣=∣a11a12a13a21a22a23a31a32a33∣a11a12a21a22a31a32=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}begin{matrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}end{matrix}=

=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a21⋅a32−a13⋅a22⋅a31−a11⋅a23⋅a32−a12⋅a21⋅a33=a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{13}cdot a_{21}cdot a_{32}-a_{13}cdot a_{22}cdot a_{31}-a_{11}cdot a_{23}cdot a_{32}-a_{12}cdot a_{21}cdot a_{33}.

Сравнивая эти два способа вычисления определителей, видим одинаковые множители, которые во втором случае немного переставлены местами.
Возможность допустить ошибку, вычисляя определитель по правилу Саррюса, намного меньше.

Примеры

Пример 1

Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по правилу Саррюса.

Приписываем два первых столбца справа от определителя и вычисляем его:

∣925148637∣921463=begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}begin{matrix}9&2\1&4\6&3end{matrix}=

=9⋅4⋅7+2⋅8⋅6+5⋅1⋅3−5⋅4⋅6−9⋅8⋅3−2⋅1⋅7=252+96+15−120−216−14=13=9cdot4cdot7+2cdot8cdot6+5cdot1cdot3-5cdot4cdot6-9cdot8cdot3-2cdot1cdot7=252+96+15-120-216-14=13.

Пример 2

Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по правилу Саррюса.

Приписываем два первых столбца справа от определителя и вычисляем его:

∣21−46−3510−1∣216−310=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}begin{matrix}2&1\6&-3\1&0end{matrix}=

=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅6⋅0−(−4)⋅(−3)⋅1−2⋅5⋅0−1⋅6⋅(−1)=6+5−12+6=5=2cdot(-3)cdot(-1)+1cdot5cdot1+(-4)cdot6cdot0-(-4)cdot(-3)cdot1-2cdot5cdot0-1cdot6cdot(-1)=6+5-12+6=5.

Существует еще одна вариация правила Саррюса. Она состоит в приписывании первой и второй строки снизу от определителя. Вычисления производятся аналогично.

Минор и алгебраическое дополнение

Прежде чем перейти к рассмотрению еще одного способа вычисления определителей 3-го порядка разберем 2 понятия: минор, алгебраическое дополнение.

Минор

Минором MijM_{ij} к элементу aija_{ij} определителя n-го порядка называется определитель (n−1)(n-1)-го порядка, который получается из исходного определителя вычеркиванием ii-той строки и jj-того столбца.

Таким образом, минор — это определитель, который остается после вычеркивания определенной строки и определенного столбца. Например, M11M_{11} получается вычеркиванием 1-й строки и 1-го столбца, M23M_{23} — вычеркиванием 2-й строки и 3-го столбца.

Алгоритм нахождения миноров:

вычеркиваем ii-ю строку;
вычеркиваем jj-й столбец;
записываем определитель, который получили в результате действий 1 и 2.

Примеры

Пример 1

Найти миноры матрицы F=(925148637)F=begin{pmatrix}9&2&5\1&4&8\6&3&7end{pmatrix}.

Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.

M11=∣925148637∣=∣4837∣=4⋅7−3⋅8=28−24=4M_{11}=begin{vmatrix}color{green}9&color{green}2&color{green}5\color{green}1&4&8\color{green}6&3&7end{vmatrix}=begin{vmatrix}4&8\3&7end{vmatrix}=4cdot7-3cdot8=28-24=4,

M12=∣925148637∣=∣1867∣=1⋅7−6⋅8=7−48=−41M_{12}=begin{vmatrix}color{green}9&color{green}2&color{green}5\1&color{green}4&8\6&color{green}3&7end{vmatrix}=begin{vmatrix}1&8\6&7end{vmatrix}=1cdot7-6cdot8=7-48=-41,

M13=∣925148637∣=∣1463∣=1⋅3−6⋅4=3−24=−21M_{13}=begin{vmatrix}color{green}9&color{green}2&color{green}5\1&4&color{green}8\6&3&color{green}7end{vmatrix}=begin{vmatrix}1&4\6&3end{vmatrix}=1cdot3-6cdot4=3-24=-21,

M21=∣925148637∣=∣2537∣=2⋅7−3⋅5=14−15=−1M_{21}=begin{vmatrix}color{green}9&2&5\color{green}1&color{green}4&color{green}8\color{green}6&3&7end{vmatrix}=begin{vmatrix}2&5\3&7end{vmatrix}=2cdot7-3cdot5=14-15=-1,

M22=∣925148637∣=∣9567∣=9⋅7−6⋅5=63−30=33M_{22}=begin{vmatrix}9&color{green}2&5\color{green}1&color{green}4&color{green}8\6&color{green}3&7end{vmatrix}=begin{vmatrix}9&5\6&7end{vmatrix}=9cdot7-6cdot5=63-30=33,

M23=∣925148637∣=∣9263∣=9⋅3−6⋅2=27−12=15M_{23}=begin{vmatrix}9&2&color{green}5\color{green}1&color{green}4&color{green}8\6&3&color{green}7end{vmatrix}=begin{vmatrix}9&2\6&3end{vmatrix}=9cdot3-6cdot2=27-12=15,

M31=∣925148637∣=∣2548∣=2⋅8−4⋅5=16−20=−4M_{31}=begin{vmatrix}color{green}9&2&5\color{green}1&4&8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}2&5\4&8end{vmatrix}=2cdot8-4cdot5=16-20=-4,

M32=∣925148637∣=∣9518∣=9⋅8−1⋅5=72−5=67M_{32}=begin{vmatrix}9&color{green}2&5\1&color{green}4&8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}9&5\1&8end{vmatrix}=9cdot8-1cdot5=72-5=67,

M33=∣925148637∣=∣9214∣=9⋅4−1⋅2=36−2=34M_{33}=begin{vmatrix}9&2&color{green}5\1&4&color{green}8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}9&2\1&4end{vmatrix}=9cdot4-1cdot2=36-2=34.

Пример 2

Найти миноры матрицы G=(21−46−3510−1)G=begin{pmatrix}2&1&-4\6&-3&5\1&0&-1end{pmatrix}.

Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.

M11=∣21−46−3510−1∣=∣−350−1∣=(−3)⋅(−1)−0⋅5=3−0=3M_{11}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\color{green}6&-3&5\color{green}1&0&-1end{vmatrix}=begin{vmatrix}-3&5\0&-1end{vmatrix}=(-3)cdot(-1)-0cdot5=3-0=3,

M12=∣21−46−3510−1∣=∣651−1∣=6⋅(−1)−1⋅5=−6−5=−11M_{12}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\6&color{green}-3&5\1&color{green}0&-1end{vmatrix}=begin{vmatrix}6&5\1&-1end{vmatrix}=6cdot(-1)-1cdot5=-6-5=-11,

M13=∣21−46−3510−1∣=∣6−310∣=6⋅0−1⋅(−3)=0+3=3M_{13}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\6&-3&color{green}5\1&0&color{green}-1end{vmatrix}=begin{vmatrix}6&-3\1&0end{vmatrix}=6cdot0-1cdot(-3)=0+3=3,

M21=∣21−46−3510−1∣=∣1−40−1∣=1⋅(−1)−0⋅(−4)=−1−0=−1M_{21}=begin{vmatrix}color{green}2&1&-4\color{green}6&color{green}-3&color{green}5\color{green}1&0&-1end{vmatrix}=begin{vmatrix}1&-4\0&-1end{vmatrix}=1cdot(-1)-0cdot(-4)=-1-0=-1,

M22=∣21−46−3510−1∣=∣2−41−1∣=2⋅(−1)−1⋅(−4)=−2+4=2M_{22}=begin{vmatrix}2&color{green}1&-4\color{green}6&color{green}-3&color{green}5\1&color{green}0&-1end{vmatrix}=begin{vmatrix}2&-4\1&-1end{vmatrix}=2cdot(-1)-1cdot(-4)=-2+4=2,

M23=∣21−46−3510−1∣=∣2110∣=2⋅0−1⋅1=0−1=−1M_{23}=begin{vmatrix}2&1&color{green}-4\color{green}6&color{green}-3&color{green}5\1&0&color{green}-1end{vmatrix}=begin{vmatrix}2&1\1&0end{vmatrix}=2cdot0-1cdot1=0-1=-1,

M31=∣21−46−3510−1∣=∣1−4−35∣=1⋅5−(−3)⋅(−4)=5−12=−7M_{31}=begin{vmatrix}color{green}2&1&-4\color{green}6&-3&5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}
1&-4\-3&5end{vmatrix}=1cdot5-(-3)cdot(-4)=5-12=-7,

M32=∣21−46−3510−1∣=∣2−465∣=2⋅5−6⋅(−4)=10+24=34M_{32}=begin{vmatrix}2&color{green}1&-4\6&color{green}-3&5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}2&-4\6&5end{vmatrix}=2cdot5-6cdot(-4)=10+24=34,

M33=∣21−46−3510−1∣=∣216−3∣=2⋅(−3)−6⋅1=−6−6=−12M_{33}=begin{vmatrix}2&1&color{green}-4\6&-3&color{green}5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}2&1\6&-3end{vmatrix}=2cdot(-3)-6cdot1=-6-6=-12.

Алгебраическое дополнение

Алгебраическим дополнением AijA_{ij} к элементу aija_{ij} определителя nn-го порядка называется число Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij},

где ii, jj — соответствующие строка и столбец,

MijM_{ij} — минор к элементу aija_{ij}.

Алгоритм нахождения алгебраических дополнений:

найти сумму номеров строки (i)(i) и столбца (j)(j);
найти минор MijM_{ij} по алгоритму нахождения миноров, который представлен выше;
подставить значения, полученные на шагах 1 и 2, в формулу Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}.

Примеры

Пример 1

Найти алгебраические дополнения матрицы F=(925148637)F=begin{pmatrix}9&2&5\1&4&8\6&3&7end{pmatrix}.

A11=(−1)1+1⋅M11=(−1)2⋅∣4837∣=4A_{11}=(-1)^{1+1}cdot M_{11}= (-1)^{2}cdotbegin{vmatrix}4&8\3&7end{vmatrix}=4,

A12=(−1)1+2⋅M12=(−1)3⋅∣1867∣=41A_{12}=(-1)^{1+2}cdot M_{12}= (-1)^{3}cdotbegin{vmatrix}1&8\6&7end{vmatrix}=41,

A13=(−1)1+3⋅M13=(−1)4⋅∣1463∣=−21A_{13}=(-1)^{1+3}cdot M_{13}= (-1)^{4}cdotbegin{vmatrix}1&4\6&3end{vmatrix}=-21,

A21=(−1)2+1⋅M21=(−1)3⋅∣2537∣=1A_{21}=(-1)^{2+1}cdot M_{21}= (-1)^{3}cdotbegin{vmatrix}2&5\3&7end{vmatrix}=1,

A22=(−1)2+2⋅M22=(−1)4⋅∣9567∣=33A_{22}=(-1)^{2+2}cdot M_{22}= (-1)^{4}cdotbegin{vmatrix}9&5\6&7end{vmatrix}=33,

A23=(−1)2+3⋅M23=(−1)5⋅∣9263∣=−15A_{23}=(-1)^{2+3}cdot M_{23}= (-1)^{5}cdotbegin{vmatrix}9&2\6&3end{vmatrix}=-15,

A31=(−1)3+1⋅M31=(−1)4⋅∣2548∣=−4A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{4}cdotbegin{vmatrix}2&5\4&8end{vmatrix}=-4,

A32=(−1)3+2⋅M32=(−1)5⋅∣9518∣=−67A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{5}cdotbegin{vmatrix}9&5\1&8end{vmatrix}=-67,

A33=(−1)3+3⋅M33=(−1)6⋅∣9214∣=34A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{6}cdotbegin{vmatrix}9&2\1&4end{vmatrix}=34.

Пример 2

Найти алгебраические дополнения матрицы G=(21−46−3510−1)G=begin{pmatrix}2&1&-4\6&-3&5\1&0&-1end{pmatrix}.

A11=(−1)1+1⋅M11=(−1)2⋅∣−350−1∣=3A_{11}=(-1)^{1+1}cdot M_{11}=(-1)^{2}cdotbegin{vmatrix}-3&5\0&-1end{vmatrix}=3,

A12=(−1)1+2⋅M12=(−1)3⋅∣651−1∣=11A_{12}=(-1)^{1+2}cdot M_{12}=(-1)^{3}cdotbegin{vmatrix}6&5\1&-1end{vmatrix}=11,

A13=(−1)1+3⋅M13=(−1)4⋅∣6−310∣=3A_{13}=(-1)^{1+3}cdot M_{13}=(-1)^{4}cdotbegin{vmatrix}6&-3\1&0end{vmatrix}=3,

A21=(−1)2+1⋅M21=(−1)3⋅∣1−40−1∣=1A_{21}=(-1)^{2+1}cdot M_{21}=(-1)^{3}cdotbegin{vmatrix}1&-4\0&-1end{vmatrix}=1,

A22=(−1)2+2⋅M22=(−1)4⋅∣2−41−1∣=2A_{22}=(-1)^{2+2}cdot M_{22}=(-1)^{4}cdotbegin{vmatrix}2&-4\1&-1end{vmatrix}=2,

A23=(−1)2+3⋅M23=(−1)5⋅∣2110∣=1A_{23}=(-1)^{2+3}cdot M_{23}=(-1)^{5}cdotbegin{vmatrix}2&1\1&0end{vmatrix}=1,

A31=(−1)3+1⋅M31=(−1)4⋅∣1−4−35∣=−7A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{4}cdotbegin{vmatrix}1&-4\-3&5end{vmatrix}=-7,

A32=(−1)3+2⋅M32=(−1)5⋅∣2−465∣=−34A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{5}cdotbegin{vmatrix}2&-4\6&5end{vmatrix}=-34,

A33=(−1)3+3⋅M33=(−1)6⋅∣216−3∣=−12A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{6}cdotbegin{vmatrix}2&1\6&-3end{vmatrix}=-12.

Зная, что такое миноры и алгебраические дополнения, рассмотрим вычисление определителя по строке и столбцу.

Вычисление определителя по строке или столбцу

Определитель матрицы равен сумме произведений элементов строки (столбца) на их алгебраические дополнения.

Алгоритм вычисления определителя по строке или столбцу:

находим алгебраические дополнения элементов строки или столбца;
находим произведения элементов на их алгебраические дополнения;
находим сумму, полученных на шаге 2, произведений.

Примеры

Пример 1

Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по 2 столбцу.

∣925148637∣=2⋅A12+4⋅A22+3⋅begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}=2cdot A_{12}+4cdot A_{22}+3cdot

A32=2(−1)3M12+4(−1)4M22+3(−1)5M32=2(−1)3∣1867∣+4(−1)4∣9567∣+3(−1)5∣9518∣=A_{32}=2(-1)^{3}M_{12}+4(-1)^{4}M_{22}+3(-1)^{5}M_{32}=2(-1)^{3}begin{vmatrix}1&8\6&7end{vmatrix}+4(-1)^{4}begin{vmatrix}9&5\6&7end{vmatrix}+3(-1)^{5}begin{vmatrix}9&5\1&8end{vmatrix}=

=−2⋅(−41)+4⋅33−3⋅67=82+132−201=13=-2cdot(-41)+4cdot33-3cdot67=82+132-201=13.

Пример 2

Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по 3 строке.

∣21−46−3510−1∣=1⋅A31+0⋅A32−1⋅A33=1(−1)4M31+0(−1)5M32−1(−1)6M33=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}=1cdot A_{31}+0cdot A_{32}-1cdot A_{33}=1(-1)^{4}M_{31}+0(-1)^{5}M_{32}-1(-1)^{6}M_{33}=

=1(−1)4∣1−4−35∣+0(−1)5∣2−465∣−1(−1)6∣216−3∣=−7+0+12=5=1(-1)^{4}begin{vmatrix}1&-4\-3&5end{vmatrix}+0(-1)^{5}begin{vmatrix}2&-4\6&5end{vmatrix}-1(-1)^{6}begin{vmatrix}2&1\6&-3end{vmatrix}=-7+0+12=5.

Любой из рассмотренных способов можно применять при нахождении определителей третьего порядка. В следующий раз мы разберем вычисление определителей матриц высших порядков.

Оформите решение задачи на заказ онлайн, если возникают трудности с выполнением!

Тест по теме «Как вычислить определитель матрицы третьего порядка»

Источник

Определитель матрицы 3 порядка, описание

Детерминант или определитель матрицы третьего порядка вида (A=begin{pmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{pmatrix}) является сопоставляемое с ним число

(left|Aright|=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-(a_{13}a_{22}a_{31}+a_{12}a_{21}a_{33}+a_{11}a_{23}a_{32}))

Для обозначения данной величины используют символы: |А|, Δ, det A.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Правила для нахождения

Для вычисления детерминанта матрицы 3×3 не нужно заучивать формулу. Данное число можно найти с помощью двух способов:

правила треугольников;
правила Саррюса.

Нахождение методом треугольника

Правило основывается на том, что произведение диагональных составляющих и произведения вершин двух треугольников уменьшаемой матрицы суммируются. Произведение диагональных элементов и произведения вершин треугольников в вычитаемой матрице записываются со знаком минус.

Схематическое изображение рассматриваемого правила выглядит так:

Матрица

По схеме можно восстановить формулу нахождения определителя матрицы третьего порядка, которая приведена в определении детерминанта:

(a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-(a_{13}a_{22}a_{31}+a_{12}a_{21}a_{33}+a_{11}a_{23}a_{32}))

Пример

Найти определитель матрицы:

(A=begin{pmatrix}1&3&4\0&2&1\1&5&-1end{pmatrix})

Решение

(left|Aright|=begin{vmatrix}21&12&14\21&12&56\25&12&14end{vmatrix}=21times12times14+12times56times25+14times12times21-14times12times25-12times56times21-21times12times14=2016)

Метод Саррюса

Для нахождения определителя матрицы 3×3 необходимо соблюсти условия в следующей последовательности:

два первых столбца приписать по левую сторону от детерминанта;
произведения компонентов главной диагонали и ей параллельных записать с положительным знаком;
произведения элементов, расположенных на побочной и параллельных ей диагоналях, записать с отрицательным знаком.

Вычисление определителя матрицы по рассматриваемому правилу схематически можно изобразить так:

Матрица 2

Пример

Рассчитать по методу Сюрраса детерминант матрицы

(A=begin{pmatrix}1&2&3\4&5&6\7&8&9end{pmatrix})

Решение

(left|Aright|=begin{vmatrix}1&2&3\4&5&6\7&8&9end{vmatrix};=begin{vmatrix}1&2&3\4&5&6\7&8&9end{vmatrix}begin{array}{c}1\4\7end{array}begin{array}{c}2\5\8end{array}=1times5times9+2times6times7+3times4times8-3times5times7-1times6times8-2times4times9=0)

Свойства определителя

Преобразование столбцов и строк незначительными действиями не оказывает влияния на значение детерминанта.
Перемена строк и столбцов местами влечет за собой изменение значения детерминанта на противоположное.
Детерминант треугольной матрицы можно вычислить путем умножения составляющих, находящихся на главной диагонали.

Источник

Определитель матрицы 3-го порядка: правило треугольника

Правило Саррюса

Методы разложения по элементам строки и столбца

Свойства определителя

Советы

Об этой статье

Была ли эта статья полезной?

Определитель матрицы.

Свойства определителя матрицы

Методы вычисления определителя матрицы

Вычисление определителя матрицы 1×1

Вычисление определителя матрицы 2×2

Вычисление определителя матрицы 3×3

Правило треугольника для вычисления определителя матрицы 3-тего порядка

Правило Саррюса для вычисления определителя матрицы 3-тего порядка

Вычисление определителя матрицы произвольного размера

Разложение определителя по строке или столбцу

Приведение определителя к треугольному виду

Теорема Лапласа

Вычисление определителей по правилу треугольника

Примеры

Вычисление определителей по правилу Саррюса

Примеры

Минор и алгебраическое дополнение

Минор

Примеры

Алгебраическое дополнение

Примеры

Вычисление определителя по строке или столбцу

Примеры

Тест по теме «Как вычислить определитель матрицы третьего порядка»

Определитель матрицы 3 порядка, описание

Правила для нахождения

Нахождение методом треугольника

Метод Саррюса

Свойства определителя

Вам также может понравиться

Как по индификатору в сбис найти контрагента

Как найти видео на телефоне нокиа

Как найти файл или папку на компьютере

Добавить комментарий Отменить ответ