Как найти диагональ боковой грани призмы формула

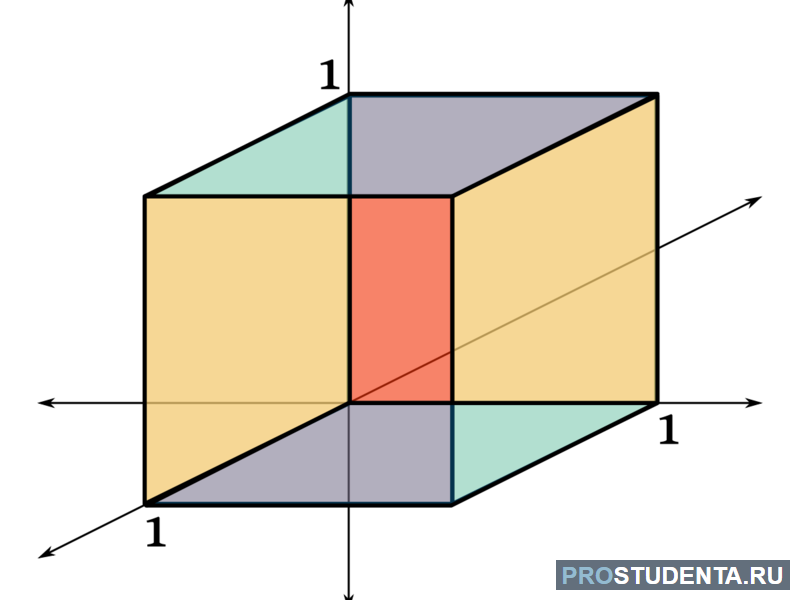
На этой странице вы узнаете

• Чем упаковка стикеров похожа на призму?
• Как можно попасть в призму в реальной жизни?
• Как сложить игральные кости из листа бумаги?
• Как найти объем воды в аквариуме? 

Слышали такое выражение «смотреть сквозь призму чего-либо»? Оно значит ситуацию, в которой мы воспринимаем что-либо под влиянием каких-то убеждений или представлений. Замысловато, конечно… Возможно, потому что и сама призма — непростое понятие. Давайте разберемся с ней с точки зрения математики.

Определение призмы

Многие из нас пользуются стикерами. Для записи своих дел, для закладок, для пометок при ведении конспектов. Даже если мы ими не пользуемся, то наверняка видели их в магазинах или у родственников и друзей. 

Один такой стикер можно принять за плоскость. Теперь вспомним, как выглядит упаковка с ними. Много-много стикеров накладываются друг на друга и получается небольшая объемная фигура, сверху и снизу которой лежат два абсолютно одинаковых листа. При этом сразу заметим, что нижний и верхний стикеры будут параллельны друг другу. 

На самом деле, упаковка со стикерами является не чем иным, как призмой! 

Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. 

Определение может показаться немного запутанным, но в нем нет ничего страшного. Разберемся, поближе взглянув на составные призмы. 

Строение призмы

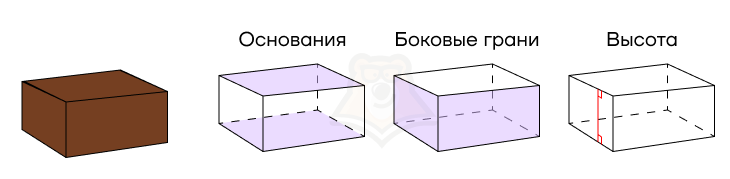
Представим себе обычную коробку. Ее дно и крышка равны между собой и лежат в параллельных плоскостях. Это и есть равные многоугольники. Также их называют основаниями призмы. 

Посмотрим на стенки коробки. Они являются параллелограммами, просто с прямыми углами. Подробнее про параллелограммы можно прочитать в статье «Параллелограмм». Эти параллелограммы называются боковыми гранями призмы. 

Возьмем линейку и измерим расстояние между основаниями призмы. Для этого из любой точки одного основания проведем перпендикуляр к другому. 

Подробнее про расстояния между плоскостями можно узнать в статьях «Углы в пространстве» и «Расстояния между фигурами». 

Может возникнуть вопрос, что мы сейчас нашли? Мы нашли высоту призмы. 

Высота призмы — перпендикуляр, опущенный из любой точки одного основания на другое основание призмы. 

В задачах намного удобнее опускать перпендикуляр не из произвольной точки, а из вершины призмы. 

Рассмотрим элементы призмы. 

Ребро — это линия пересечения двух плоскостей. 

Представим, что вместо картонных стенок в нашей коробке ткань, которую нам нужно натянуть на каркас так, чтобы коробка не изменилась. В этом случае все прямые этого каркаса и будут ребрами.

Ребра бывают двух видов: 

• ребра оснований,
• боковые ребра. 

Отличить их также легко: ребра основания являются стороной многоугольника, который в нем лежит, в то время как боковые ребра не принадлежат основаниям. 

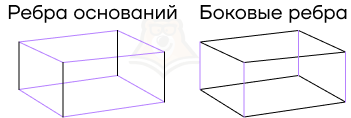
У боковых ребер есть одно очень важное свойство: они равны между собой и параллельны. 

Диагональ призмы — отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. 

Например, мы можем взять клетку попугая и от угла до угла сделать ему жердочку, чтобы птичке было весело жить. Эта жердочка и будет диагональю призмы. 

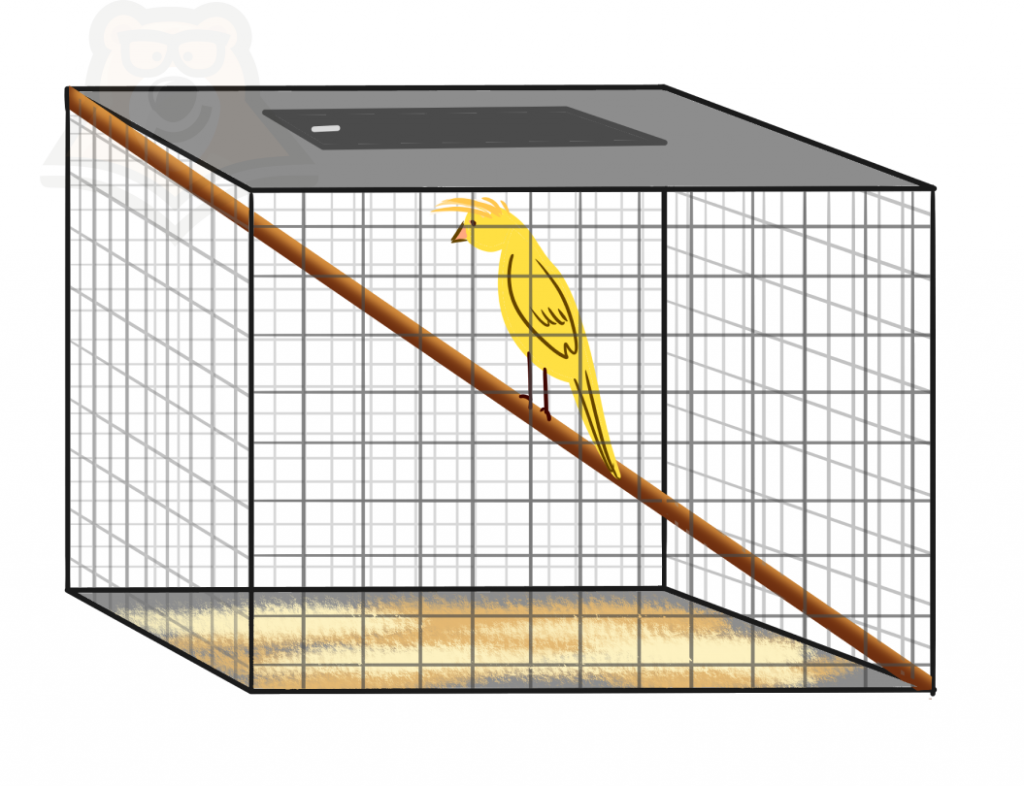
Виды призм

Вернемся к рассуждениям о том, чем упаковка стикеров похожа на призму. Например, куб и параллелепипед будут отличаться. А если в основании призмы будет лежать треугольник или шестиугольник? Или двадцатиугольник? Разделим призмы на несколько видов.

Мы рассмотрим две классификации. 

В первом случае будем рассматривать призмы по фигурам, которые лежат в основании. В многоугольнике может быть множество сторон, а значит, и в основании призмы может быть треугольник, четырехугольник, шестиугольник, десятиугольник и так далее. 

В зависимости от фигуры в основании призмы могут называться по-разному. Вот три основных, которые чаще всего встречаются при решении заданий:

• треугольная призма,

• четырехугольная призма,

• шестиугольная призма. 

Аналогичным образом можно дать название любой призме, например, десятиугольная призма или стоугольная призма. 

В определении призмы сказано, что в боковых гранях лежат параллелограммы. До этого мы чертили только прямоугольники, но в боковых гранях могут лежать не только они. 

С этим связана вторая классификация призм. По этому признаку призмы делятся всего на два вида:

• прямые,
• наклонные. 

Разберемся в них чуть подробнее. 

Прямая призма — призма, боковые ребра которой перпендикулярны основаниям. 

В этом случае боковые ребра и ребра оснований действительно образовывают прямоугольник. 

Наклонная призма — призма, боковые ребра которой находятся под углом к основаниям. 

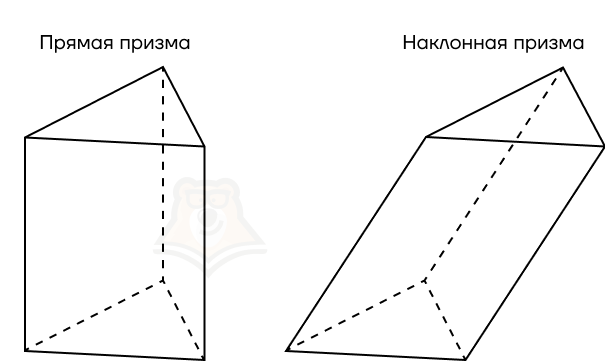
Где мы можем найти прямые и наклонные призмы? Оказывается, в архитектуре. Обычный жилой дом типовой застройки будет прямой призмой. А вот примером наклонной призмы может служить комплекс зданий “Ворота Европы” в Мадриде. 

Чуть подробнее остановимся на прямых призмах. Они встречаются достаточно часто и обладают несколькими важными свойствами. 

Посмотрите на свою комнату. Если по плану квартиры она будет многоугольником, то вы как бы сидите в призме. Теперь ответим на вопрос: как найти высоту комнаты? 

Простой ответ: померить по стене. А если посмотреть на угол, то можно заметить, что ребро призмы совпадает с высотой. Таким образом, мы получаем первое свойство прямых призм. 

Свойство 1. Высота прямой призмы совпадает с её боковым ребром. 

Посмотрим на стены комнаты, на их форму. Они все являются прямоугольниками, верно? 

Свойство 2. Все боковые грани прямой призмы — прямоугольники. 

Если мы в основании прямой призмы разместим правильный многоугольник, у нас получится правильная призма.

Правильная призма — прямая призма, в основании которой лежит правильный многоугольник. 

Например,  в правильной треугольной призме будет лежать равносторонний треугольник, а в правильной шестиугольной призме — правильный шестиугольник. 

Определение параллелепипеда

Еще одной разновидностью прямоугольной призмы является параллелепипед. 

Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. 

Параллелепипеды встречаются повсюду: коробки, мебель, комнаты, здания, склады, магазины. Поэтому изучить их не составит труда. 

Свойство параллелепипеда, видимое невооруженным глазом: противоположные грани параллелепипеда равны. Как пример, вспомним ту же комнату: потолок и пол равны, так же как и стены, находящиеся напротив друг друга. 

Нельзя не упомянуть про одно очень важное свойство параллелепипеда: 

• Все его диагонали пересекаются в одной точке и этой точкой делятся пополам. Это свойство справедливо для всех видов параллелепипеда. 

Какие бывают параллелепипеды? 

Параллелепипеды также бывают прямыми и наклонными. В этих случаях все определения такие же, как и для всех остальных призм. 

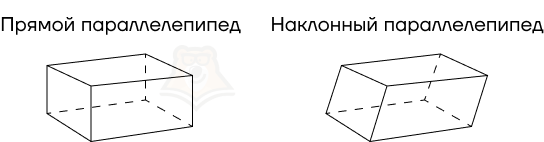
Прямой параллелепипед

Рассмотрим несколько интересных свойств прямого параллелепипеда. 

1 свойство. Боковые ребра прямого параллелепипеда перпендикулярны основаниям. 

2 свойство. Высота прямоугольного параллелепипеда равна длине его бокового ребра. 

3 свойство. Боковые грани, которые лежат напротив друг друга, равны между собой и являются прямоугольниками. 

Прямые параллелепипеды можно разделить еще на два вида:

• Прямой параллелепипед: в основании лежит параллелограмм;

• Прямоугольный параллелепипед: в основании лежит прямоугольник. 

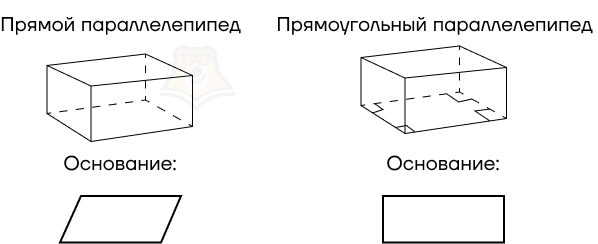
Рассмотрим свойства прямоугольного параллелепипеда. 

1 свойство. Все грани прямоугольного параллелепипеда являются прямоугольниками. 

2 свойство. Все углы в прямоугольном параллелепипеде, образованные двумя гранями, равны 90°. 

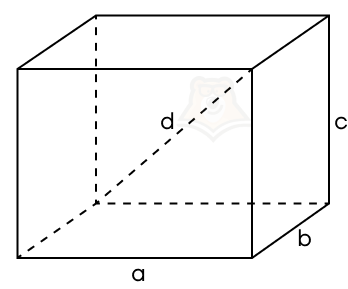
3 свойство. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин его ширины, длины и высоты. 

Таким образом, мы получаем важную формулу для параллелепипеда. 

d² = a² + b² + c²

Пример 1. Дан прямоугольный параллелепипед. Два ребра, выходящие из одной его вершины, равны (sqrt{35}) и (sqrt{46}). Диагональ параллелепипеда равна 15. Найдите третье ребро параллелепипеда. 

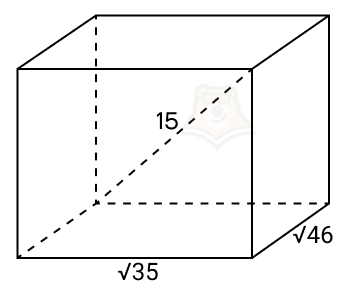
Решение. Пусть третье ребро параллелепипеда равняется х. Получаем уравнение:

(15^2 = (sqrt{35})^2 + (sqrt{46})^2 + x^2)
225 = 35 + 46 + x²
x² = 144
x = 12

Ответ: 12. 

У прямоугольного параллелепипеда существует еще несколько видов. Прямоугольные параллелепипеды делятся на:

• Произвольный прямоугольный параллелепипед. В основании может лежать прямоугольник. 

• Правильный прямоугольный параллелепипед. В основании лежит правильный четырехугольник, то есть квадрат. 
  При этом боковые ребра не равны ребрам основания. Следовательно, в основаниях будут лежать квадраты, а в боковых гранях прямоугольники. 

• Куб. В основании лежит квадрат, а боковые ребра равны ребрам основания. 
  В кубе все ребра равны, а все его грани будут квадратом. 

Таким образом, мы рассмотрели все виды параллелепипеда. 

Формулы для призмы

Однако ни одна задача не может быть решена без формул. Поэтому необходимо рассмотреть несколько основных формул, которые могут встретиться не только в задачах, но и в жизни. 

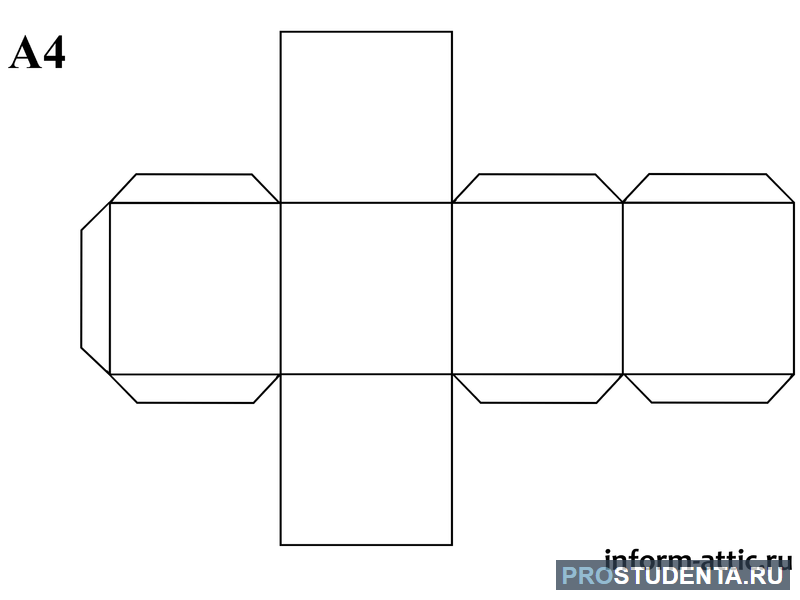
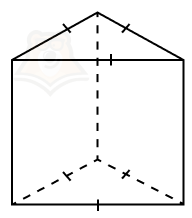
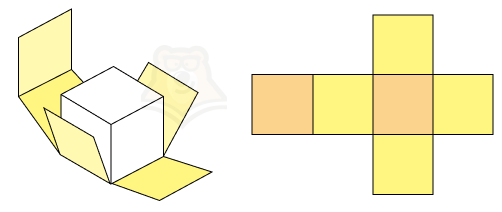
Немного вспомним моделирование, а именно развертку кубика. Мы знаем, что из листа бумаги без труда можно сложить кубик, если правильно его вычертить. 

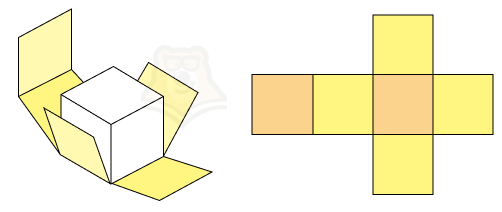
На рисунке оранжевым показаны основания, а желтым боковые грани нашего будущего кубика. А теперь представим, что нам нужно найти площадь боковой поверхности. Как это сделать?

Нужно найти площади желтых квадратиков и сложить их. 

Площадь боковой поверхности призмы — сумма площадей всех боковых ее граней. 

Единой формулы тут нет, поскольку призмы могут очень сильно отличаться друг от друга. В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать. 

Но есть один фокус! Правда, он работает только для прямой призмы. Если по условию дана прямая призма, то можно воспользоваться формулой 

S_бок. = P * h

В этой формуле Р — периметр основания, h — высота призмы, которая совпадает с высотой боковой грани. 

Пример 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равняется 2, а высота 10. 

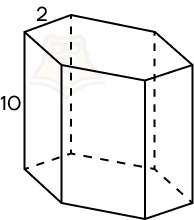
Решение. 

Шаг 1. Поскольку правильная призма по определению прямая, мы можем воспользоваться формулой S = Ph. 

Шаг 2. В основании правильной призмы лежит правильный шестиугольник, следовательно, периметр основания будет равен 6 * 2 = 12. 

Шаг 3. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 12 * 10 = 120. 

Ответ: 120. 

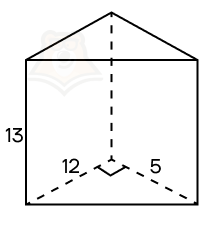
Пример 2. Дана прямая треугольная призма, в основании которой лежит прямоугольный треугольник с катетами 12 и 5. Высота призмы равна 13. Найдите площадь ее боковой поверхности. 

Решение. 

Шаг 1. Поскольку призма прямая, можно воспользоваться формулой S = Ph. 

Шаг 2. Найдем периметр основания. Для этого необходимо найти гипотенузу треугольника. Воспользуемся теоремой Пифагора: (sqrt{12^2 + 5^2} = sqrt{144 + 25} = sqrt{169} = 13). 

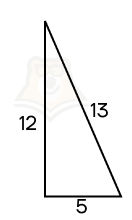
Шаг 3. Найдем периметр основания: P = 12 + 5 + 13 = 30. 

Шаг 4. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 30 * 13 = 390. 

Ответ: 390. 

Мы научились находить площадь боковой поверхности. А как найти всю площадь призмы? Вспомним нашу развертку с кубиком. Чтобы найти всю площадь кубика, нужно найти площадь всех квадратов, из которых он состоит. То есть и площадь боковой поверхности, и площадь оснований. 

Площадь полной поверхности призмы — сумма площадей всех граней. 

Следовательно, нам нужно сложить площади всех боковых граней и дважды площадь основания. Получаем следующую формулу. 

S = S_бок + 2S_осн

Вспомним обычный хлеб, черный или белый. Его форма очень приближена к параллелепипеду. Тогда его корочка будет площадью полной поверхности параллелепипеда. А все что внутри, то есть мякиш, можно принять за объем. 

Пример 3. Дана прямая призма, в основании которой лежит ромб с диагоналями 12 и 16. Боковое ребро призмы равно 25. Найдите площадь поверхности призмы. 

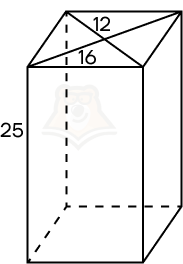
Решение. 

Шаг 1. Найдем площадь основания. Площадь ромба можно найти по формуле (frac{1}{2} * D_1 * D_2). Следовательно, площадь ромба равна (frac{1}{2} * 12 * 16 = 96). 

Шаг 2. Заметим, что диагонали ромба образуют четыре равных прямоугольных треугольника. Следовательно, чтобы найти сторону ромба, достаточно рассмотреть прямоугольный треугольник с катетами 6 и 8. По теореме Пифагора сторона ромба будет равна (sqrt{6^2 + 8^2} = sqrt{36 + 64} = sqrt{100} = 10).

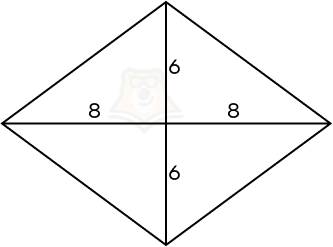
Шаг 3. Периметр ромба будет равен 4 * 10 = 40. Тогда площадь боковой поверхности равна 40 * 25 = 1000. 

Шаг 4. Площадь полной поверхности будет равняться 1000 + 2 * 96 = 1000 + 192 = 1192.

Ответ: 1192

Пример 4. Площадь поверхности правильной четырехугольной призмы равняется 1980. Сторона основания равна 5. Найдите боковое ребро этой призмы. 

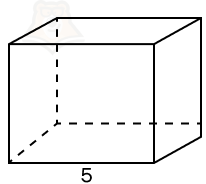
Решение. 

Шаг 1. Воспользуемся формулой S = S_бок + 2S_осн. Площадь основания будет равняться площади квадрата, то есть 5 * 5 = 25. 

Шаг 2. Подставим известные величины в формулу: 

1980 = S_бок + 2 * 25
S_бок = 1930

Шаг 3. Площадь боковой поверхности равна произведению периметра основания на высоту призмы. Периметр равен 5 * 4 = 20. Тогда получаем уравнение:

20h = 1930
h = 96,5

Шаг 4. Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5.

Ответ: 96,5. 

Теперь рассмотрим, как найти объем призмы. Допустим, мы налили в прямоугольный аквариум немного воды. Как определить, сколько воды мы налили?

Для этого достаточно воспользоваться формулой объема призмы. 

V = S_осн. * h

Эта формула общая, однако для каждой призмы она может принять свой вид в зависимости от того, какую формулу нужно использовать для поиска площади основания или высоты. 

Например, чтобы найти объем воды в аквариуме, необходимо длину умножить на ширину и на высоту, а значит формула принимает вид V = abh. 

Пример 5. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы. 

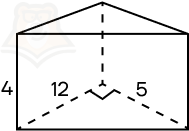
Решение. 

Шаг 1. Для начала найдем площадь основания. В этом случае мы можем воспользоваться формулой (frac{1}{2}ab). Площадь равна (frac{1}{2} * 12 * 15 = 90).

Шаг 2. Воспользуемся формулой объема призмы и подставим известные величины: 

V = 90 * 4 = 360.

Ответ: 360. 

Пример 6. Дан сосуд, в основании которого лежит правильный треугольник. В этот сосуд налили 3000 см³ воды. Высота жидкости оказалась равной 10 см. После этого в сосуд опустили шарик и высота изменилась с 10 см на 14 см. Найдите объем шарика. 

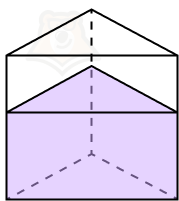
Решение. Немного вспомним физику, а именно тот факт, что объем вытесненной жидкости равен объему тела. Значит, чтобы найти объем шарика, необходимо найти насколько изменился объем воды. 

Шаг 1. Найдем площадь основания сосуда. Для этого немного преобразуем формулу объема: 
(S = frac{V}{h})
Тогда:
(S = frac{3000}{10} = 300)

Шаг 2. А теперь найдем объем после того, как в воду погрузили шарик. Он будет равен 300 * 14 = 4200. 

Шаг 3. Объем вытесненной жидкости равен 4200 — 3000 = 1200.

Ответ: 1200. 

Мы рассмотрели основные формулы, которые применяются для решения задач. Стоит заметить, что они универсальны, и в каждой задаче их рационально преобразовывать под ситуацию. 

Фактчек 

• Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. Равные многоугольники называются основаниями призмы, а остальные стороны — боковыми гранями. В призме есть ребра — линии пересечения двух ее граней. Ребра как бы образуют каркас призмы. 
• Призмы можно разделить на несколько видов по тому, какая фигура лежит в основании: треугольник, четырехугольник, шестиугольник или любой другой многоугольник. Призмы бывают прямые и наклонные. В прямых призмах боковые ребра перпендикулярны основанию, а в наклонных — нет. Правильная призма — прямая призма, в основании которой лежит правильный многоугольник. 
• Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. Параллелепипеды бывают наклонными и прямыми. Прямые параллелепипеды включают в себя прямоугольные параллелепипеды, которые, в свою очередь, делятся на произвольные, правильные и кубы. 
• В призме можно найти площадь боковой поверхности, площадь полной поверхности и объем. Для каждого из этих случаев необходимо пользоваться формулами. 

Проверь себя

Задание 1.
Что такое диагональ призмы?

1. Отрезок, соединяющий две соседние вершины в призме.
2. Отрезок, соединяющий противоположные углы в боковой грани призмы.
3. Отрезок, соединяющий противоположные углы в основании призмы.
4. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.  

Задание 2.
Что такое прямая призма?

1. Призма, боковые ребра которой перпендикулярны основаниям.
2. Призма, боковые ребра которой расположены под острым углом относительно основания.
3. Призма, боковые ребра которой расположены под тупым углом относительно основания.
4. Призма, в основании которой лежит прямоугольник.

Задание 3.
Как найти высоту прямой призмы?

1. Высоту нужно найти с помощью оснований.
2. Высота совпадает с боковым ребром.
3. Необходимо найти расстояние между двумя вершинами, не принадлежащими одной грани.
4. В прямой призме невозможно найти высоту. 

Задание 4.
Какая фигура лежит в основании прямоугольного параллелепипеда?

1. Параллелограмм с острыми углами.
2. Ромб с острыми углами.
3. Трапеция.
4. Прямоугольник. 

Задание 5. 
Как найти площадь полной поверхности призмы?

1. Нужно найти сумму площадей всех боковых граней.
2. Нужно сложить площадь боковой поверхности и площадь основания.
3. Нужно сложить площадь боковой поверхности и удвоенную площадь основания.
4. Нужно сложить площади оснований. 

Ответы: 1. — 4 2. — 1 3. — 2 4. — 4 5. — 3

Призма является геометрической объемной фигурой, характеристики и свойства которой изучают в старших классах школ. Как правило, при ее изучении рассматривают такие величины, как объем и площадь поверхности. В данной же статье раскроем несколько иной вопрос: приведем методику определения длины диагоналей призмы на примере четырехугольной фигуры.

Какая фигура называется призмой?

В геометрии дается следующее определение призме: это объемная фигура, ограниченная двумя многоугольными одинаковыми сторонами, которые параллельны друг другу, и некоторым числом параллелограммов. Рисунок ниже показывает пример призмы, соответствующий данному определению.

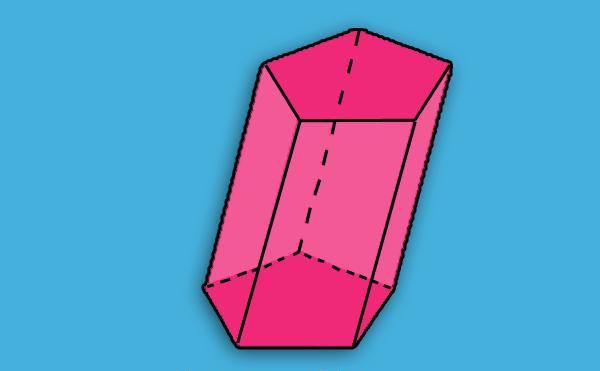
Мы видим, что два красных пятиугольника равны друг другу и находятся в двух параллельных плоскостях. Пять розовых параллелограммов соединяют эти пятиугольники в цельный объект – призму. Два пятиугольника называются основаниями фигуры, а ее параллелограммы – это боковые грани.

Призмы бывают прямые и наклонные, которые также называют прямоугольными и косоугольными. Разница между ними заключается в углах между основанием и боковыми гранями. Для прямоугольной призмы все эти углы равны 90^o.

По количеству сторон или вершин многоугольника в основании говорят о призмах треугольных, пятиугольных, четырехугольных и так далее. Причем если этот многоугольник является правильным, а сама призма прямой, то такую фигуру называют правильной.

Приведенная на предыдущем рисунке призма является пятиугольной наклонной. Ниже же изображена пятиугольная прямая призма, которая является правильной.

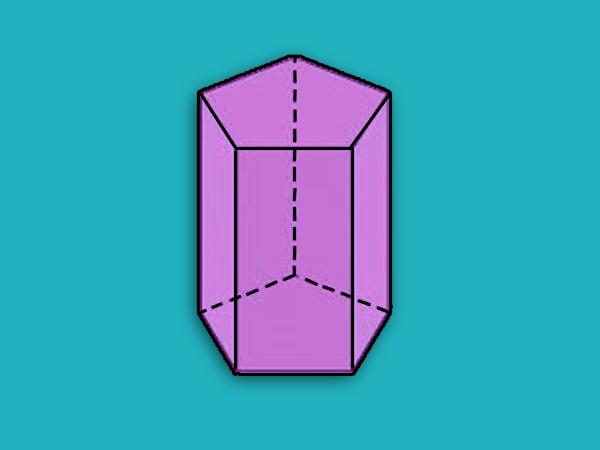
Все вычисления, включая методику определения диагоналей призмы, удобно выполнять именно для правильных фигур.

Какие элементы характеризуют призму?

Элементами фигуры называют составные части, которые ее образуют. Конкретно для призмы можно выделить три главных типа элементов:

• вершины;
• грани или стороны;
• ребра.

Гранями считаются основания и боковые плоскости, представляющие параллелограммы в общем случае. В призме всегда каждая сторона относится к одному из двух типов: либо это многоугольник, либо параллелограмм.

Ребра призмы – это те отрезки, которые ограничивают каждую сторону фигуры. Как и грани, ребра также бывают двух типов: принадлежащие основанию и боковой поверхности или относящиеся только к боковой поверхности. Первых всегда в два раза больше, чем вторых, независимо от вида призмы.

Вершины – это точки пересечения трех ребер призмы, два из которых лежат в плоскости основания, а третье – принадлежит двум боковым граням. Все вершины призмы находятся в плоскостях оснований фигуры.

Числа описанных элементов связаны в единое равенство, имеющее следующий вид:

Р = В + С – 2.

Здесь Р – количество ребер, В – вершин, С – сторон. Это равенство называется теоремой Эйлера для полиэдра.

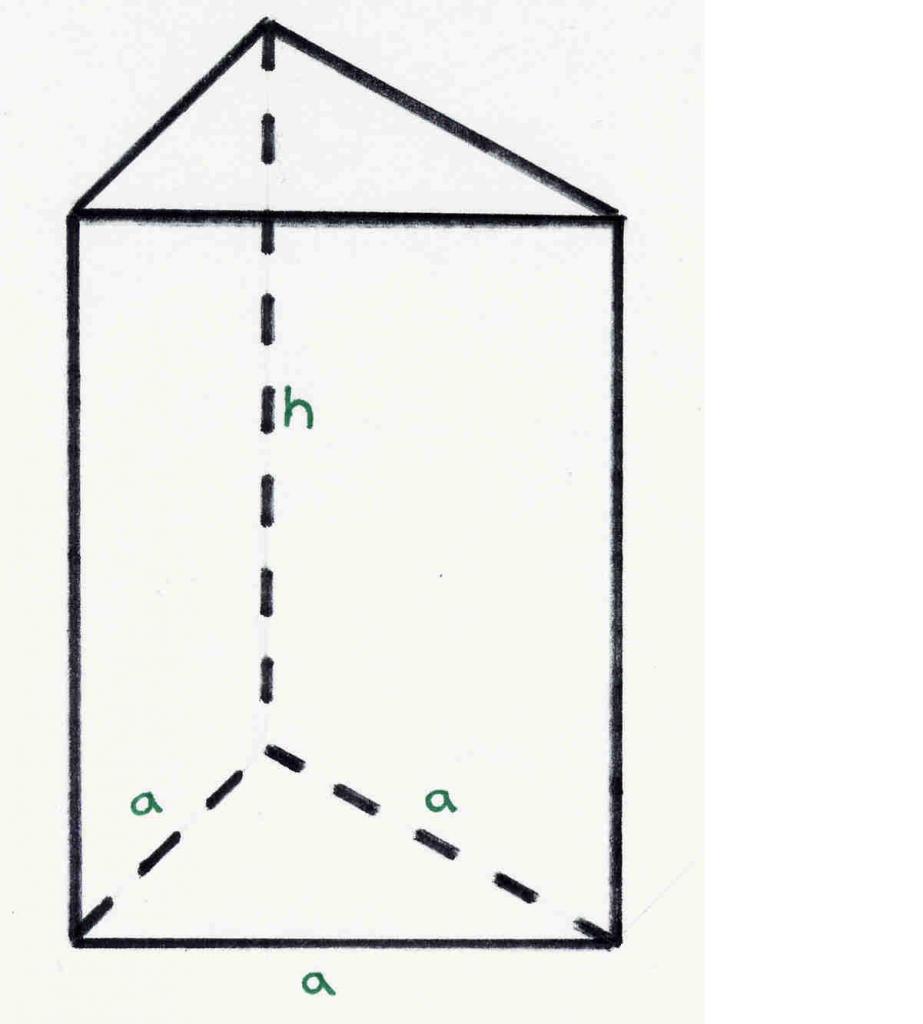
На рисунке показана треугольная правильная призма. Каждый может посчитать, что она имеет 6 вершин, 5 сторон и 9 ребер. Эти цифры согласуются с теоремой Эйлера.

Диагонали призмы

После таких свойств, как объем и площадь поверхности, в задачах по геометрии часто встречается информация о длине той или иной диагонали рассматриваемой фигуры, которая либо дана, либо ее нужно найти по другим известным параметрам. Рассмотрим, какие бывают диагонали у призмы.

Все диагонали можно разделить на два типа:

1. Лежащие в плоскости граней. Они соединяют несоседние вершины либо многоугольника в основании призмы, либо параллелограмма боковой поверхности. Значение длин таких диагоналей определяется, исходя из знания длин соответствующих ребер и углов между ними. Для определения диагоналей параллелограммов всегда используются свойства треугольников.
2. Лежащие внутри объема призмы. Эти диагонали соединяют неоднотипные вершины двух оснований. Эти диагонали оказываются полностью внутри фигуры. Их длины рассчитать несколько сложнее, чем для предыдущего типа. Методика расчета предполагает учет длин ребер и основания, и параллелограммов. Для прямых и правильных призм расчет является относительно простым, поскольку он осуществляется с использованием теоремы Пифагора и свойств тригонометрических функций.

Далее приведем примеры вычисления различных диагоналей.

Диагонали сторон четырехугольной прямой призмы

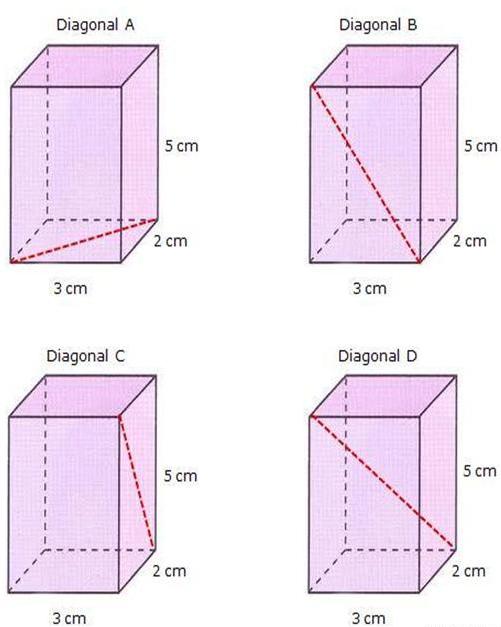
На рисунке выше изображены четыре одинаковые прямые призмы, и даны параметры их ребер. На призмах Diagonal A, Diagonal B и Diagonal C штриховой красной линией изображены диагонали трех разных граней. Поскольку призма является прямой с высотой 5 см, а ее основание представлено прямоугольником со сторонами 3 см и 2 см, то отыскать отмеченные диагонали не представляет никакого труда. Для этого необходимо воспользоваться теоремой Пифагора.

Длина диагонали основания призмы (Diagonal A) равна:

D_A = √(3²+2²) = √13 ≈ 3,606 см.

Для боковой грани призмы диагональ равна (см. Diagonal B):

D_B = √(3²+5²) = √34 ≈ 5,831 см.

Наконец, длина еще одной боковой диагонали равна (см. Diagonal C):

D_С = √(2²+5²) = √29 ≈ 5,385 см.

Длина внутренней диагонали

Теперь рассчитаем длину диагонали четырехугольной призмы, которая изображена на предыдущем рисунке (Diagonal D). Сделать это не так сложно, если заметить, что она является гипотенузой треугольника, в котором катетами будут высота призмы (5 см) и диагональ D_A , изображенная на рисунке вверху слева (Diagonal A). Тогда получаем:

D_D = √(D_A²+5²) = √(2 ²+3²+5²) = √38 ≈ 6,164 см.

Правильная призма четырехугольная

Диагональ правильной призмы, основанием которой является квадрат, рассчитывается аналогичным образом, как и в приведенном выше примере. Соответствующая формула имеет вид:

D = √(2*a²+c²).

Где a и c – длины стороны основания и бокового ребра, соответственно.

Заметим, что при вычислениях мы использовали только теорему Пифагора. Для определения длин диагоналей правильных призм с большим числом вершин (пятиугольные, шестиугольные и так далее) уже необходимо применять тригонометрические функции.

Как найти диагональ правильной призмы

Нахождение диагонали правильной призмы часто используется как промежуточный этап при решении более сложных задач. Общая формула легко выводится при рассмотрении двух прямоугольных треугольников.

Инструкция

Для нахождения диагонали правильной призмы вам необходимо разобраться всего в нескольких определениях.

Призмой называется многогранник, имеющий в качестве оснований два равных многоугольника (треугольника, четырехугольника и т.д.), лежащих в параллельных плоскостях, а в качестве боковых граней – параллелограммы.
Прямой призмой называется призма, у которой боковые грани-прямоугольники.
Правильной призмой называется прямая призма, основания которой являются правильными многоугольниками (равносторонний треугольник, квадрат, и т.д.)
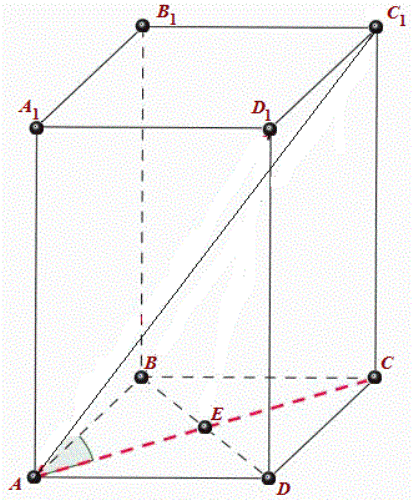
АВСDА1В1С1D1 – Правильная четырехугольная призма.
АА1В1В – боковая грань правильной четырехугольной призмы.
Все четыре боковых грани данной призмы равны.
АВСD и А1В1С1D1 -основания призмы (квадраты, лежащие в параллельных плоскостях).
Диагональю многогранника называется отрезок, соединяющий две его не смежные вершины, т.е вершины, которые не принадлежат одной грани.
Из рисунка видно, что точка А и точка С 1 не принадлежат одной грани и следовательно отрезок АС1 – диагональ данной призмы.

Для того чтобы найти диагональ, призмы надо рассмотреть треугольник АСС1. Этот треугольник прямоугольный. Диагональ призмы АС1 в рассматриваемом треугольнике будет являться гипотенузой, а отрезки АС и СС1 катетами. Из теоремы Пифагора (в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов) следует, что:
АС12 = АС2 + СС12 (1);

Далее следует рассмотреть треугольник АСD. Треугольник АСD тоже прямоугольный (т.к. основание призмы – квадрат). Для удобства можно обозначить сторону основания буквой а. Таким образом по теореме Пифагора:
АС2 = а2 +а2, АС = √2а (2);

Если обозначить высоту призмы буквой h и подставить выражение (2) в выражение (1), получится:
АС12 = 2а2+h2, АС1 = √(2a^2+h^2 ), где а – сторона основания, h – высота.
Данная формула справедлива для любой правильной призмы.

Источники:

• диагональная призма

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

В школьной программе по курсу стереометрии изучение объёмных фигур обычно начинается с простого геометрического тела — многогранника призмы. Роль её оснований выполняют 2 равных многоугольника, лежащих в параллельных плоскостях. Частным случаем является правильная четырёхугольная призма. Её основами являются 2 одинаковых правильных четырёхугольника, к которым перпендикулярны боковые стороны, имеющие форму параллелограммов (или прямоугольников, если призма не наклонная).

Оглавление:

• Как выглядит призма
• Площадь поверхности и объём
• Нахождение элементов призмы
• Примеры задач с решениями
• Как найти площадь куба

В школьной программе по курсу стереометрии изучение объёмных фигур обычно начинается с простого геометрического тела — многогранника призмы. Роль её оснований выполняют 2 равных многоугольника, лежащих в параллельных плоскостях. Частным случаем является правильная четырёхугольная призма. Её основами являются 2 одинаковых правильных четырёхугольника, к которым перпендикулярны боковые стороны, имеющие форму параллелограммов (или прямоугольников, если призма не наклонная).

Как выглядит призма

Правильной четырёхугольной призмой называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками. Иное название для этой геометрической фигуры — прямой параллелепипед.

Рисунок, на котором изображена четырёхугольная призма, показан ниже.

На картинке также можно увидеть важнейшие элементы, из которых состоит геометрическое тело. К ним принято относить:

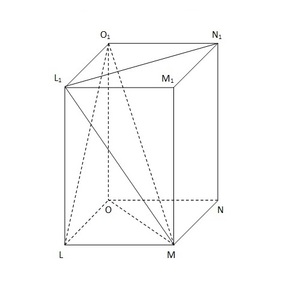1. Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
2. Боковые грани — прямоугольники MM₁L₁L, LL₁O₁O, NN₁O₁O и MM₁N₁N, расположенные под прямым углом к основаниям.
3. Боковые рёбра — отрезки, расположенные на стыке между двумя боковыми гранями: M₁M, N₁N, O₁O и L₁L. Также выполняют роль высоты (поскольку лежат в параллельной основаниям плоскости). В призме боковые рёбра всегда равны между собой — это одно из важнейших свойств этого геометрического тела.
4. Диагонали, которые, в свою очередь, подразделяются ещё на 3 категории. К ним относится 4 диагонали основания (MO, N₁L₁), 8 диагоналей боковых граней (ML₁, O₁L) и 4 диагонали призмы, начала и концы которых являются вершинами 2 разных оснований и боковых сторон (MO₁, N₁L).

Иногда в задачах по геометрии можно встретить понятие сечения. Определение будет звучать так: сечение — это все точки объёмного тела, принадлежащие секущей плоскости. Сечение бывает перпендикулярным (пересекает рёбра фигуры под углом 90 градусов). Для прямоугольной призмы также рассматривается диагональное сечение (максимальное количество сечений, которых можно построить — 2), проходящее через 2 ребра и диагонали основания.

Если же сечение нарисовано так, что секущая плоскость не параллельна ни основам, ни боковым граням, в результате получается усечённая призма.

Для нахождения приведённых призматических элементов используются различные отношения и формулы. Часть из них известна из курса планиметрии (например, для нахождения площади основания призмы достаточно вспомнить формулу площади квадрата).

Площадь поверхности и объём

Чтобы определить объём призмы по формуле, необходимо знать площадь её основания и высоту:

V = Sосн·h

Так как основанием правильной четырёхгранной призмы является квадрат со стороной a, можно записать формулу в более подробном виде:

V = a²·h

Если речь идёт о кубе — правильной призме с равной длиной, шириной и высотой, объём вычисляется так:

V = a³

Чтобы понять, как найти площадь боковой поверхности призмы, необходимо представить себе её развёртку.

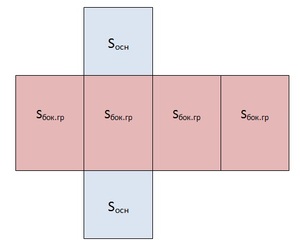
Из чертежа видно, что боковая поверхность составлена из 4 равных прямоугольников. Её площадь вычисляется как произведение периметра основания на высоту фигуры:

Sбок = Pосн·h

С учётом того, что периметр квадрата равен P = 4a, формула принимает вид:

Sбок = 4a·h

Для куба:

Sбок = 4a²

Для вычисления площади полной поверхности призмы нужно к боковой площади прибавить 2 площади оснований:

Sполн = Sбок + 2Sосн

Применительно к четырёхугольной правильной призме формула имеет вид:

Sполн = 4a·h + 2a²

Для площади поверхности куба:

Sполн = 6a²

Зная объём или площадь поверхности, можно вычислить отдельные элементы геометрического тела.

Нахождение элементов призмы

Часто встречаются задачи, в которых дан объём или известна величина боковой площади поверхности, где необходимо определить длину стороны основания или высоту. В таких случаях формулы можно вывести:

• длина стороны основания: a = Sбок / 4h = √(V / h);
• длина высоты или бокового ребра: h = Sбок / 4a = V / a²;
• площадь основания: Sосн = V / h;
• площадь боковой грани: Sбок. гр = Sбок / 4.

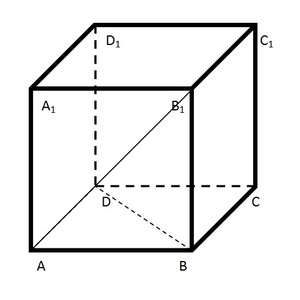Чтобы определить, какую площадь имеет диагональное сечение, необходимо знать длину диагонали и высоту фигуры. Для квадрата d = a√2. Из этого следует:

Sдиаг = ah√2

Для вычисления диагонали призмы используется формула:

dприз = √(2a² + h²)

Чтобы понять, как применять приведённые соотношения, можно попрактиковаться и решить несколько несложных заданий.

Примеры задач с решениями

Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.

Задание 1.

В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?

Решение.

Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:

V₁ = ha² = 10a²

Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:

V₂ = h (2a)² = 4ha²

Поскольку V₁ = V₂, можно приравнять выражения:

10a² = 4ha²

После сокращения обеих частей уравнения на a² получается:

10 = 4h

В результате новый уровень песка составит h = 10 / 4 = 2,5 см.

Задание 2.

ABCDA₁B₁C₁D₁ – правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.

Решение.

Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.

Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.

Длина любого ребра определяется через известную диагональ:

a = d / √2 = 6√2 / √2 = 6

Площадь полной поверхности находится по формуле для куба:

Sполн = 6a² = 6·6² = 216

Задание 3.

В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?

Решение.

Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.

Длина комнаты составляет a = √9 = 3 м.

Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².

Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.

Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.

Как найти площадь куба