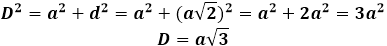Как найти диагональ единичного куба - Сайт, где вы сможете решить свои вопросы

Куб является базовым геометрическим телом, когда речь заходит об объеме и объемных телах. Недаром третья степень, которая получается умножением трех одинаковых чисел друг на друга (как при нахождении объема куба – трех его измерений одинаковых измерений) названа в его честь.

Основным и единственным параметром куба является его ребро a,так как все ребра у куба конгруэнтны, и представляют собой одновременно и длину, и ширину, и высоту. Соответственно, всего одно значение определяет все возможные характеристики куба, связанные с его измерениями.

Помимо ребер, вершины куба можно соединить диагоналями. Диагонали могут проходить через грани куба, тогда они будут просто диагональю основания или диагональю квадрата в плоскости, либо диагонали могут быть проведены внутри самого куба, соединяя противоположные основания в крайних точках (вершинах).

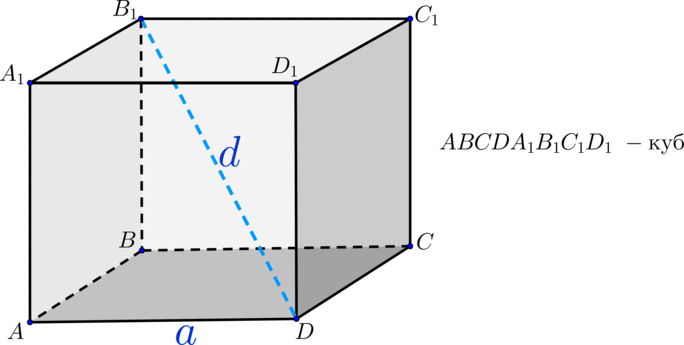
Чтобы найти диагональ куба через его ребро, необходимо сначала провести дополнительное построение в виде диагонали одного из соединяемых оснований, тогда диагональ куба станет гипотенузой новоиспеченного прямоугольного треугольника, катетами которого являются ребро куба и диагональ основания. Если ребро куба задано условиями задачи, то диагональ квадрата в основании придется сначала вычислить по формуле:
d=a√2

Тогда диагональ куба можно будет выразить через теорему Пифагора, и она примет следующий вид:

Источник

Куб. Формулы, признаки и свойства куба

Определение.

Куб (гексаедр) — это трехмерная фигура, которая состоит из шести динаковых квадратов так, что каждый квадрат полностью соприкасается своими четырьмя сторонами к сторонам остальных четырех квадратов под прямым углом. Куб является правильным многогранником, у которого грани образованы из квадратов. Также кубом можно назвать прямоугольный параллелепипед, у которого все ребра равны.

Определение. Грань куба – это часть плоскости, ограниченная сторонами квадрата.

– куб имеет шесть граней;

– каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная шестой грани;

– грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата.

Определение. Ребро куба – это отрезок, образованный пересечением двух граней куба.

– куб имеет двенадцать ребер;

– каждый конец ребра соединен с двумя соседними ребрами под прямым углом;

– ребра куба имеют одинаковую длину.

Определение. Вершина куба – это самая отдаленная от центра куба точка, которая лежит на пересечения трех граней куба.

– куб имеет восемь вершин;

– каждая вершина образована только тремя гранями и тремя ребрами.

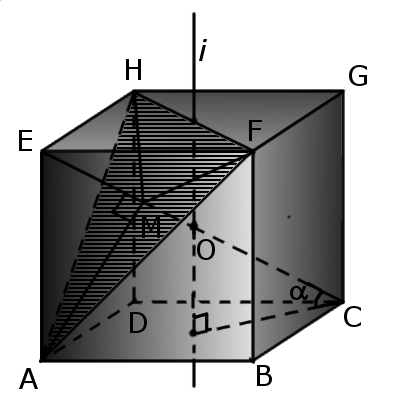
Определение. Центр грани куба (O₁) – это равноудалена точка от всех ребер грани куба.

Определение. Центр куба (O) – это равноудалена точка от всех граней куба.

Определение. Ось куба (i) – это прямая, проходящая через центр куба и центры двух параллельных граней куба.

– куб имеет три оси;

– оси куба взаимно перпендикулярны.

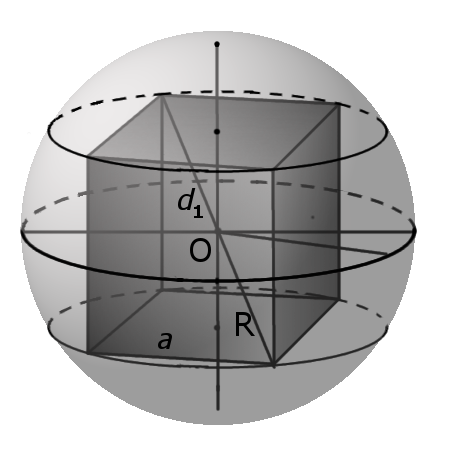
Определение. Диагональ куба (d₁) – отрезок, который соединяет противоположные вершины куба и проходит через центр куба.

– куб имеет четыре диагонали;

– диагонали куба пересекаются и делятся пополам в центре куба;

– диагонали куба имеют одинаковую длину.

Формула. Диагональ куба d₁ через длину ребра a:

d₁ = a√3

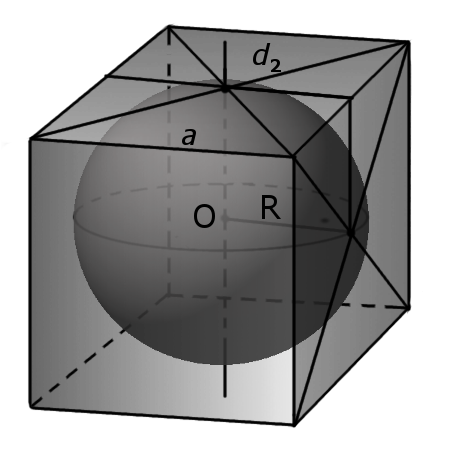
Определение. Диагональ грани куба (d₂) -отрезок, который соединяет противоположные углы грани куба и проходит через центр грани куба.

Формула. Диагональ грани d₂ через длину ребра a:

d₂ = a√2

Определение. Объём куба – это совокупность всех точек в пространстве, ограниченные гранями куба.

Формула. Объём куба через длину ребра a:

V = a³

Формула. Объём куба через длину диагонали куба d₁:

Определение. Площадь поверхности куба – это совокупность плоскостей всех граней.

Формула. Площадь поверхности куба через длину ребра a:

S = 6a²

Определение. Периметр куба – это совокупность длин всех ребер куба.

Формула. Периметр куба P через длину ребра a:

P = 12a

Определение. Сферой вписанной в куб называется сфера, центр которой совпадает с центром куба и которая касается центров граней куба.

– все шесть граней куба являются касательными плоскостями к вписанной сферы;

– радиус вписанной сферы равен половине длины ребра a.

Формула. Радиус вписанной сферы r через длину ребра a:

Формула. Объема вписанной сферы V через длину ребра a:

Определение. Сферой описанной вокруг куба называется сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами куба.

– радиус описанной сферы равен половине длины диагонали (d₁) куба.

Формула. Радиус описанной сферы R через длину ребра a:

Формула. Объема сферы описанной вокруг куба V через длину ребра a:

Свойства куба

1. В куб можно вписать тетраэдр так, чтобы все четыре вершины тетраэдра лежали на четырех вершинах куба, а все шесть ребер тетраэдра будут лежать на шести гранях куба и ребра будут равны диагонали грани куба.

2. В куб можно вписать правильный шестиугольник так, что все шесть вершин лежат в центрах граней куба.

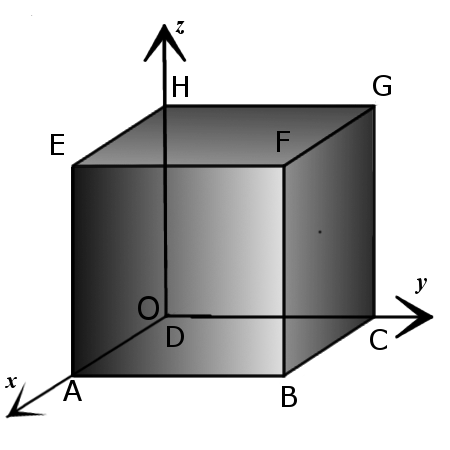
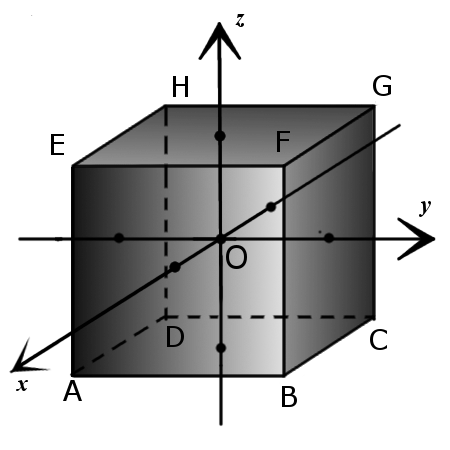
Координаты вершин куба

1. Координаты вершин куба со стороной a и вершиной D в начале декартовой системы координат так, что ребра этой вершины лежат на осях координат:

A(a, 0, 0),
B(a, a, 0),
C(0, a, 0),
D(0, 0, 0),
E(a, 0, a),
F(a, a, a),
G(0, a, a),
H(0, 0, a).

2. Координаты вершин куба с длиной стороны 2a, у которого центр куба находится в начале декартовой системы координат так, что ребра куба параллельны осям координат:

A(a, –a, –a),
B(a, a, –a),
C(-a, a, –a),
D(-a, –a, –a),
E(a, –a, a),
F(a, a, a),
G(-a, a, a),
H(-a, –a, a).

Определение. Единичный куб – это куб, у которого длина ребер равна единице.

Пересечение куба плоскостью

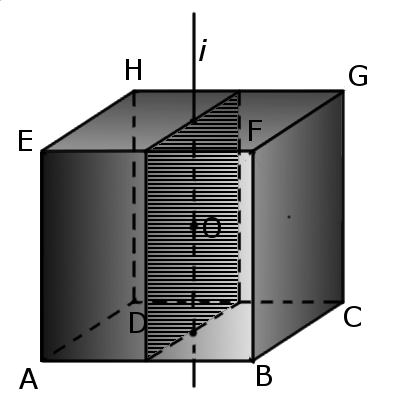
1. Если пересечь куб плоскостью, проходящей через центр куба и центры двух противоположных граней, то в сечении будет квадрат, длина стороны которого будет равна длине ребра куба. Эта плоскость делит куб два равных прямоугольных параллелепипеда.

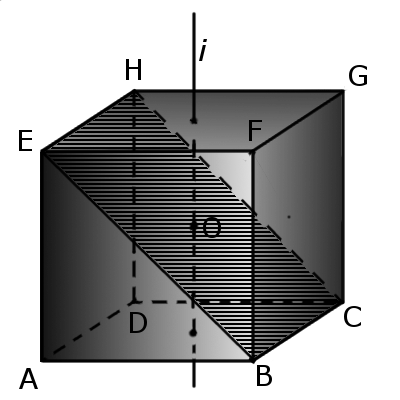
2. Если пересечь куб с ребром a плоскостью, проходящей через центр куба и два параллельных ребра, то в сечении будет прямоугольник со сторонами a и a√2, площадью сечения a²√2. Эта плоскость делит куб две равные призмы.

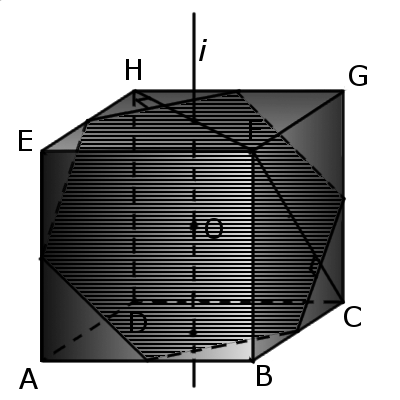
3. Если пересечь куб плоскостью, проходящей через центр и середины шести граней, то в сечении будет правильный шестиугольник со стороной a√2/2, площадью сечения a²(3√3)/4. У куба одна из диагоналей (FC) каждой грани, что пересекаются, перпендикулярна стороне шестиугольника.

4. Если пересечь куб плоскостью, проходящей через три вершины куба, то в сечении будет правильный треугольник со стороной a√2, площадью сечения a²√3/2 и объемом большей части – 5a³/6 и меньшей – a³/6. Одна из диагоналей куба (EC) перпендикулярна к плоскости сечения и проходит через центр треугольника (M) и делится плоскостью в отношении MC:EМ = 2:1.

Источник

Факт 1.
(bullet) Куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.
(bullet) Следовательно:

— ({color{red}{{small{объем куба}}}}) ищется по следующей формуле (где (a) – ребро куба): [{color{red}{{large{V=a^3}}}}] — ({color{red}{{small{диагональ куба}}}}) [{color{red}{{large{d^{,2}=3a^2}}}}] — ({color{red}{{small{площадь поверхности куба}}}}) равна сумме площадей шести одинаковых квадратов, т.е. [{color{red}{{large{S_{text{пов.куб}}=6a^2}}}}]

Факт 2.
(bullet) Если сфера вписана в куб (то есть касается всех его граней), то ее радиус равен (0,5a), где (a) – ребро куба.
(bullet) Если сфера описана около куба (то есть все вершины куба лежат на сфере), то ее радиус равен (0,5d), где (d) – диагональ куба.
(bullet) Центр сферы, вписанной в куб или описанной около куба, лежит в точке пересечения диагоналей куба.

Источник

Диагональ куба – это отрезок, соединяющий вершину верхнего основания с вершиной нижнего основания, лежащей напротив, таким образом, что диагональ проходит сквозь внутреннее пространство куба под углом 45 градусов. Для того чтобы найти диагональ куба, достаточно знать его ребро и правильно оформить чертеж. Если провести диагональ нижнего основания из той же вершины, что и диагональ куба, то мы получим внутри куба прямоугольный треугольник, сторонами которого будут ребро куба, диагональ основания и сама диагональ куба. Для того чтобы найти диагональ куба в этом треугольнике по теореме Пифагора, необходимо сначала найти диагональ основания. Так как в основании куба лежит квадрат, то его диагональ равна , где a – сторона квадрата, совпадающая с ребром куба. Получаем, что катеты необходимого треугольника равны и a, а гипотенуза равна корню из суммы их квадратов:

Источник

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

Определение куба
Свойства куба
- Свойство 1
- Свойство 2
- Свойство 3
Формулы для куба
- Диагональ
- Диагональ грани
- Площадь полной поверхности
- Периметр ребер
- Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

Куб

Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A₁, B₁, C₁ и D₁.
Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA₁, BB₁, CC₁, DD₁, A₁B₁, B₁C₁, C₁D₁ и A₁D₁.
Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A₁B₁C₁D₁, AA₁B₁B, BB₁C₁C, CC₁D₁D и AA₁D₁D.