Длина дуги сегмента круга по хорде и высоте — онлайн-калькулятор
Формулы расчета длины дуги
Длина дуги вычисляется по стандартной формуле (1), однако в этом расчете все переменные неизвестны, соответственно их нужно вывести из других формул геометрии круга. Радиус круга (4) выражается через формулы хорды (2) и высоты сегмента (3), по этим же формулам можно получить значение угла сегмента (5).
R = h/2 + W 2 /(8 × h) (4)
α = 2 × arcsin[W / (2 × R)] (5)
Как найти окружность зная хорду
Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.
Сегмент круга
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина окружности
О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r — радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π — математическая константа, примерно равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Длина дуги сегмента круга по хорде и высоте — онлайн-калькулятор
Формулы расчета длины дуги
Длина дуги вычисляется по стандартной формуле (1), однако в этом расчете все переменные неизвестны, соответственно их нужно вывести из других формул геометрии круга. Радиус круга (4) выражается через формулы хорды (2) и высоты сегмента (3), по этим же формулам можно получить значение угла сегмента (5).
R = h/2 + W 2 /(8 × h) (4)
α = 2 × arcsin[W / (2 × R)] (5)
Формула длины дуги через хорду
На практике часто требуется найти длину дуги, данной на чертеже или в натуре, причем неизвестно, какую часть окружности составляет дуга и каков ее радиус. В таких случаях используют формулу Гюйгенса.
На дуге отмечают середину M. Она лежит на перпендикуляре СM, проведенном к хорде AB через середину хорды C. Далее измеряют хорды AB и AM. Длина дуги выражается через формулу Гюйгенса так:
Относительная погрешность этой формулы составляет 0.5%, когда дуга AB содержит 60°. С уменьшением угловой меры дуги процент погрешности резко падает. Для дуги в 45° относительная погрешность составляет примерно 0.02%.
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.
Сегмент круга
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Сегмент
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Гибочный калькулятор
Чаще всего стоит задача определения параметров дуги по её габаритным размерам. Для этого мы предлагаем гибочный калькулятор.
Введите значения H и h в миллиметрах
хорда
H = мм
высота хорды
h = мм
радиус
R = 0 мм
длина дуги
L = 0 мм
угол сегмента
φ = 0 градусов
Очистить
Вычислить
Сохранить расчёт
Не забывайте, что для гибки профилей необходим технологический припуск от 500 до 1000 мм. на заготовку.
Вы можете скачать ПК версию гибочного калькулятора по этой ссылке.
140030, МО, Люберецкий район, пос. Малаховка, Касимовское шоссе, д. 3Г
Право собственности ООО “ПК РАДИУС” © 2002–2017. Все права защищены.
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/kak-nayti-okruzhnost-znaya-hordu
http://planshet-info.ru/kompjutery/formula-dliny-dugi-cherez-hordu
[/spoiler]
Быстро найти диагональ квадрата, которая также является диаметром описанной окружности при наличии последней, можно при помощи этого онлайн-калькулятора. Для этого просто впишите одно из известных значений, будь то площадь квадрата, периметр, одну из сторон или радиусы вписанной/описанной окружностей, в свободную ячейку и нажмите на кнопку “Рассчитать”. В результате отобразится не только диагональ квадрата, но и все вышеперечисленные значения.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
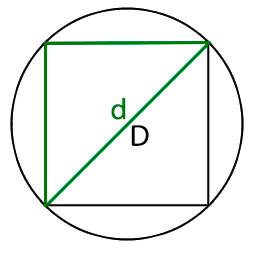
При помощи нашего калькулятора вы легко сможете узнать диагональ вписанного в круг квадрата.
Для того что бы найти диагональ вписанного в круг квадрата, нам необходимо узнать диаметр круга в который вписан квадрат при этом диагональ квадрата (d) и диаметр круга (D) равны.
D = d
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Теперь для того что бы найти диагональ треугольника (которая равна диаметру) нам необходимо перейти к следующему шагу
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=P/π
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=2R
Соответственно если мы знаем диаметр круга мы знаем и длину диагонали квадрата,
d=D

Внимательно прочитаем задание и определим данные, которые нам понадобятся в процессе решения. Нам дан квадрат с вписанной в него окружностью и дан ее радиус. Значит нужно вспомнить свойства данных фигур и их взаимосвязь с друг другом.
Первый способ решения
Первый способ нахождения ответа основывается на формуле диагонали квадрата: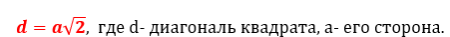
Зная эту формулу алгоритм наших действий, следующий:
-
-найти сторону квадрата;
-
– подставить найденное значение в формулу;
-
– вычислить;
-
– записать ответ.

А можно ли решить данную задачу иначе? Да, конечно! Для этого рассмотрим другой способ.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
![]()
Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисления
Знаков после запятой: 2
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
![]()
Параметры сегмента по хорде и высоте
Точность вычисления
Знаков после запятой: 2
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
![]()
Площадь сегмента круга по радиусу и высоте
Точность вычисления
Знаков после запятой: 2
Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
- длина дуги
- угол
- хорда
- высота
- радиус
- площадь
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
![]()
Круговой сегмент – все варианты расчета
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
