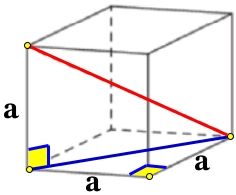
Формулировка задачи: Объем куба равен V. Найдите его диагональ.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
Пример задачи:
Объем куба равен 24√3. Найдите его диагональ.
Решение:
Сторону куба можно получить из его объема:
a3 = 24√3 = (2√3)3
a = 2√3
Теперь можно вычислить диагональ куба по его стороне:
d = a ⋅ √3 = 2√3 ⋅ √3 = 6
Ответ: 6
В общем виде решение данной задачи по стереометрии выглядит следующим образом:
a = ∛V – сторона куба
d = a ⋅ √3 = ∛V ⋅ √3 – диагональ куба
где V – объем куба.
Остается лишь подставить конкретные значения и подсчитать результат.
Поделитесь статьей с одноклассниками «Дан объем куба, найдите его диагональ – как решать».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
Задания
Версия для печати и копирования в MS Word
Тип 2 № 27099
i
Объем куба равен
Найдите его диагональ.
Спрятать решение
Решение.
Если ребро куба равно a, то его объем и диагональ даются формулами и
Следовательно,
Тогда диагональ равна 6.
Ответ: 6.
Аналоги к заданию № 27099: 74431 628742 628768 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Спрятать решение
·
Видеокурс
·
Помощь
Решение:
Найдём из формулы объёма куба, сторону куба а:
V = a3 = 24√3
a3 = 8·3·√3
a3 = 23·√32·√31
a3 = 23·√32+1
a3 = 23·√33
a3 = (2·√3)3
a = 2·√3
В прямоугольном треугольнике, по теореме Пифагора, найдём диагональ основания куба:
d2 = a2 + a2
d2 = (2·√3)2 + (2·√3)2
d2 = 4·3 + 4·3
d2 = 24
d = √24
В прямоугольном треугольнике, по теореме Пифагора, найдём диагональ куба:
D2 = a2 + d2
D2 = (2·√3)2 + (√24)2
D2 = 12 + 24
D2 = 36
D = √36 = 6
Ответ: 6.
Диагональ куба – это отрезок, который находится во внутреннем пространстве куба, благодаря тому, что его вершины находятся на противоположных сторонах. Поэтому для того чтобы представить диагональ куба в алгебраическом виде, необходимо заключить ее в фигуру, соединив данную диагональ и боковое ребро, исходящее из любой вершины диагонали через диагональ основания. Получив, таким образом, прямоугольный треугольник, можно составить отношение сторон по теореме Пифагора и вывести формулу для диагонали куба. Ребро куба будет равно отношению диагонали к корню из трех.
a^2+d^2=D^2
D^2=a^2+2a^2
D^2=3a^2
D=a√3
a=D/√3
Площадь стороны куба равна ребру куба, возведенному во вторую степень, площадь боковой поверхности представляет собой четыре таких площади стороны, а площадь полной поверхности состоит из 6 граней. Площади куба, выраженные через диагональ, принимают следующий вид:
S=a^2=D^2/3
S_(б.п.)=4a^2=(4D^2)/3
S_(п.п.)=6a^2=2D^2
Объем куба равен его ребру в третьей степени, а объем куба, зная диагональ куба, будет равен диагонали, возведенной в третью степень, и деленной на три корня из трех.
V=a^3=D^3/(3√3)
Чтобы вычислить периметр куба, нужно ребро куба умножить на двенадцать. Если выразить периметр грани через диагональ куба, то он примет вид отношения диагонали, умноженной на четыре корня из трех.
P=12a=4√3 D
Чтобы найти диагональ стороны куба, то есть диагональ, лежащую на боковой грани, можно воспользоваться формулой диагонали квадрата, которая выглядит как произведение стороны квадрата/ребра куба на корень из двух.
d=a√2=(D√2)/√3
Радиус вписанной в куб сферы равен половине ребра куба, то есть диагонали куба, деленной на два корня из трех, а радиус описанной вокруг куба сферы равен половине самой диагонали куба. (рис. 2.2, рис.2.3)
r=a/2=D/(2√3)
R=D/2