Формулировка задачи: Площадь поверхности куба равна S. Найдите его диагональ.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
Пример задачи:
Площадь поверхности куба равна 18. Найдите его диагональ.
Решение:
Площадь поверхности куба равна сумме площадей всех его граней. У куба 6 одинаковых граней. Если мы возьмем 1 сторону за a, то площадь поверхности куба будет равна:
6 ⋅ a2 = 18
Найдем из полученного равенства сторону куба:
Осталось найти диагональ куба. Для этого нужно воспользоваться формулой:
d = a ⋅ √3 = √3 ⋅ √3 = 3
Ответ: 3
В общем виде решение данной задачи по стереометрии выглядит следующим образом:
a = √S / 6 – сторона куба
d = a ⋅ √3 = √S / 6 ⋅ √3 = √S / 2 – диагональ куба
где S – площадь поверхности куба.
Остается лишь подставить конкретные значения и подсчитать результат.
Поделитесь статьей с одноклассниками «Дана площадь поверхности куба, найдите его диагональ – как решать».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
Макс Нескажу
Мыслитель
(9818)
12 лет назад
По теореме пифагора.
Диагональ – гипотенуза
Ширина и длина у куба – катеты и они одинаковы.
И формула гипотенуза в квадрате=высота в квадрате + ширина в квадрате.
Ну площадь поверхности куба – квадрат же.
Ну вот к примеру – площадь – 16
Значит высота=ширина=4
Значит диагональ равна х^2=4^2+4^2
И равна корень из 32
Казаков Сергей
Знаток
(314)
12 лет назад
я думаю, что для начала надо узнать площадь одной стороны, т. к. сторон шесть и они все равны, то и общую площадь надо поделить на шесть. дальше узнать длину грани, то есть корень квадратный и т. д.
Источник: моя голова
- Дисциплина: Математика базовая
- Номер вопроса в билете: 13
- Баллы: 1
- Сложность: Базовый
- Площадь поверхности куба равна 242. Найдите его диагональ.
- Подробное решение
-
Площадь поверхности куба считается как сумма шести площадей граней(квадратов), которые являются сторонами этого куба
Пусть ребро куба равно a, тогда площадь одной его грани a2 а так как таких граней 6 штук, следовательно площадь всей поверхности куба равна:
S=6a2S=6a^2
Найдем a2a^2
242=6a2a2=2426=1213242=6a^2\
{a^2= displaystyle{242over6}={121over3}}Корень извлекать нет смысла, так как дальше нам понадобиться Теорема Пифагора
Найдем диагональ куба:
диагональ куба – это гипотенуза.
один катет равен а
второй катет – это диагональ основания куба, то есть квадрата со сторонами а, и равенb=a2+a2b=sqrt{a^2+a^2}
d2=b2+a2d2=(a2+a2)2+a2d2=3a2d2=3⋅1213=121d=11d^2=b^2+a^2\
d^2=(sqrt{a^2+a^2})^2 +a^2\
d^2=3a^2\
{{d^2=3cdotdisplaystyle{121over3}=121}}\
d=11Ответ: 11
Пространственная диагональ куба при заданной общей площади поверхности Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 3D геометрия ↺ | |
| 3D геометрия | Платоновы тела ↺ | |
| Платоновы тела | куб ↺ | |
| куб | Диагональ куба ↺ | |
| Диагональ куба | Космическая диагональ куба ↺ |
|
✖Общая площадь поверхности куба — это количество плоскостей, заключенных на всей поверхности куба.ⓘ Общая площадь поверхности куба [TSA] |
+10% -10% |
|
✖Пространственная диагональ Куба — это расстояние от любого угла до противоположного и самого дальнего угла Куба.ⓘ Пространственная диагональ куба при заданной общей площади поверхности [dSpace] |
⎘ копия |
Пространственная диагональ куба при заданной общей площади поверхности Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Общая площадь поверхности куба: 600 Квадратный метр –> 600 Квадратный метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
17.3205080756888 метр –> Конверсия не требуется
14 Космическая диагональ куба Калькуляторы
7 Диагональ куба Калькуляторы
Пространственная диагональ куба при заданной общей площади поверхности формула
Космическая диагональ куба = sqrt(Общая площадь поверхности куба/2)
dSpace = sqrt(TSA/2)
Что такое куб?
Куб — это симметричная замкнутая трехмерная фигура, имеющая 6 одинаковых граней квадратной формы. У него 8 углов, 12 ребер и 6 граней. И каждый угол разделяется на 3 грани, а каждое ребро — на 2 грани Куба. Другими словами, прямоугольный ящик, в котором длина, ширина и высота численно равны, называется кубом. Это равное измерение называется длиной ребра куба. Также куб является платоновым телом.
Площадь поверхности куба равна – найдите диагональ
Условие задачи :Площадь поверхности куба равна 18 – найдите диагональ
Условие нашей задачи таково, что имеется в наличии площадь куба, которая равна 18 и нужно узнать диагональ данного куба!? И мы решим эту задачку двумя способами!
Способ номер 1.
Если в вашей задаче диагональ не равна 18, то вы можете решить вашу задачку смотры на наше решение данной задачки в качестве примера!
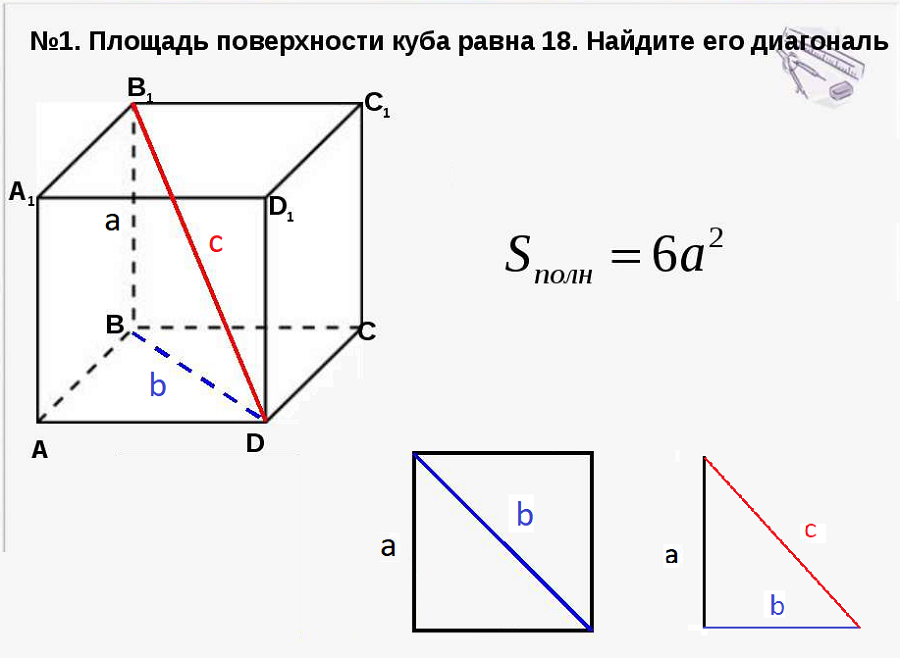
Решение задачи : Площадь поверхности куба равна 18 – найдите диагональ
Как мы знаем, у диагонали куба есть своя формула – она нам понадобится! И из нее нам потребуется выразить сторона а через с
с = a√3 => a = c/√3
И далее возьмём площадь и заменим сторону а на верхнее выражение
S = 6a2 => S = 6c2/3 => 2c2
Ответ задачи : Площадь поверхности куба равна 18 – найдите диагональ
Отсюда выведем чему равна диагональ:
2c2 = S = 18 => c2 = 18/2 => с = √9 = 3
Ответ, диагональ куба площадью 18 равна 3
Способ номер 2.
Это второй вариант задач, по сути – это доказательство формулы диагонали куба..
Решение задачи : Площадь поверхности куба равна 18 – найдите диагональ
Выведем чему равна сторона куба если известна площадь из формулы:
S = 18 = 6a2 a2 = 18/6 => a = √3
Нам понадобится формула пифагора Посмотрим на картинку и нас интересует нижний квадрат и частный случай формулы Пифагора для равных сторон треугольника:
b2 = 2a2
Подставляем ранее выведенное ребро a в эту формулу и получаем:
b = 2(√3)2 = √6
Следующим шагом нам нужен треугольник, в котором уже интересует диагональ и поступаем аналогично что и чуть выше, полученный результата вставляем в формулу и ползучем диагональ куба…
c2 = a2 + b2 => (√3)2 + (√6)2 = 9 => с = √9 => с = 3
Ответ и втрое решение у нас получился ответ точно такой же – 3 диагональ куба с площадью 18
Написать что-нибудь…
площадь поверхности куба равна ,
площадь поверхности куба объем равен ,
площадь поверхности куба равна найдите диагональ ,
площадь поверхности куба равна найдите его ,
площадь поверхности куба равна найдите ,
