Куб является базовым геометрическим телом, когда речь заходит об объеме и объемных телах. Недаром третья степень, которая получается умножением трех одинаковых чисел друг на друга (как при нахождении объема куба – трех его измерений одинаковых измерений) названа в его честь.
Основным и единственным параметром куба является его ребро a,так как все ребра у куба конгруэнтны, и представляют собой одновременно и длину, и ширину, и высоту. Соответственно, всего одно значение определяет все возможные характеристики куба, связанные с его измерениями.
Помимо ребер, вершины куба можно соединить диагоналями. Диагонали могут проходить через грани куба, тогда они будут просто диагональю основания или диагональю квадрата в плоскости, либо диагонали могут быть проведены внутри самого куба, соединяя противоположные основания в крайних точках (вершинах).
Чтобы найти диагональ куба через его ребро, необходимо сначала провести дополнительное построение в виде диагонали одного из соединяемых оснований, тогда диагональ куба станет гипотенузой новоиспеченного прямоугольного треугольника, катетами которого являются ребро куба и диагональ основания. Если ребро куба задано условиями задачи, то диагональ квадрата в основании придется сначала вычислить по формуле:
d=a√2
Тогда диагональ куба можно будет выразить через теорему Пифагора, и она примет следующий вид:
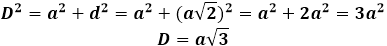
Куб или как его еще называют гексаэдр – это правильный многогранник, каждая из граней которого имеет форму квадрата. Куб – это частный случай призмы и параллелепипеда.
Разные дисциплины используют значение этого термина по отношению к различным свойствам геометрического прототипа. Например, в аналитике применяют аналитические многомерные кубы, которые позволяют наглядно сопоставить данные из разных таблиц.
Свойства куба
- В куб можно вписать тетраэдр двумя вариантами, причем вершины тетраэдра, а их четыре, будут совпадать с четырьмя вершинами куба. Все шесть ребер тетраэдра будут располагаться на всех шести гранях куба и будут равны диагонали грани квадрата.
- Четыре сечения куба это правильные шестиугольники, они проходят по центру куба перпендикулярно четырем диагоналям.
- В куб вписывается октаэдр, причем все шесть вершин октаэдра совместятся с центрами шести граней куба.
- Куб вписывается в октаэдр, причем все восемь вершин куба расположатся в центрах восьми граней октаэдра.
- В куб можно вписать икосаэдр, так, что шесть взаимно параллельных ребер икосаэдра расположатся на шести гранях куба, остальные двадцать четыре ребра внутри куба, все 12 вершин икосаэдра лягут по шести граням куба.
Формулы для куба
- Поверхность куба: A = 6*a2
- Объем куба: V = a3
- Диагональ куба: d = a*√3
Диагональ куба
Диагональ
Правильный многогранник, все грани которого являются квадратами, называется кубом. Все ребра у куба равны, а углы прямые. Диагональ стороны куба d или его боковой грани, представляющей собой квадрат, определяем по формуле диагонали квадрата, как произведение стороны квадрата (ребра куба) (а) на корень квадратный из двух: d=a√2
Диагональю куба является отрезок, который соединяет две вершины, расположенные на противоположных сторонах куба. Вершины расположены симметрично по отношению к центру куба. Для определения диагонали куба вписываем в куб прямоугольный треугольник, соединив диагональ куба, диагональ основания и боковое ребро, исходящее из вершины основания. Воспользовавшись теоремой Пифагора, вычисляем диагональ куба, которая равна произведению ребра куба (а) на корень квадратный из трех.
Калькулятор для расчета диагонали куба
Факт 1.
(bullet) Куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.
(bullet) Следовательно:
— ({color{red}{{small{объем куба}}}}) ищется по следующей формуле (где (a) – ребро куба): [{color{red}{{large{V=a^3}}}}] — ({color{red}{{small{диагональ куба}}}}) [{color{red}{{large{d^{,2}=3a^2}}}}] — ({color{red}{{small{площадь поверхности куба}}}}) равна сумме площадей шести одинаковых квадратов, т.е. [{color{red}{{large{S_{text{пов.куб}}=6a^2}}}}]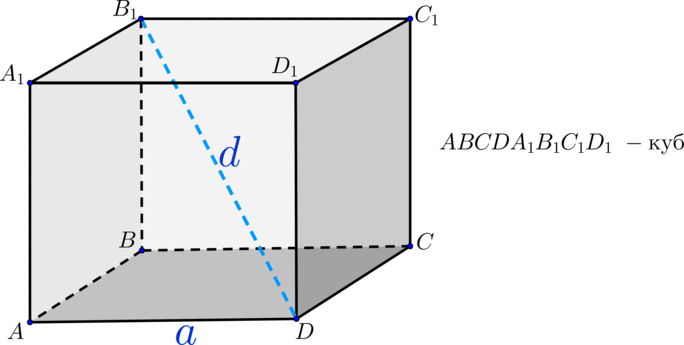 
Факт 2.
(bullet) Если сфера вписана в куб (то есть касается всех его граней), то ее радиус равен (0,5a), где (a) – ребро куба.
(bullet) Если сфера описана около куба (то есть все вершины куба лежат на сфере), то ее радиус равен (0,5d), где (d) – диагональ куба.
(bullet) Центр сферы, вписанной в куб или описанной около куба, лежит в точке пересечения диагоналей куба.
Диагональ куба – это отрезок, соединяющий вершину верхнего основания с вершиной нижнего основания, лежащей напротив, таким образом, что диагональ проходит сквозь внутреннее пространство куба под углом 45 градусов. Для того чтобы найти диагональ куба, достаточно знать его ребро и правильно оформить чертеж. Если провести диагональ нижнего основания из той же вершины, что и диагональ куба, то мы получим внутри куба прямоугольный треугольник, сторонами которого будут ребро куба, диагональ основания и сама диагональ куба. Для того чтобы найти диагональ куба в этом треугольнике по теореме Пифагора, необходимо сначала найти диагональ основания. Так как в основании куба лежит квадрат, то его диагональ равна 
, где a – сторона квадрата, совпадающая с ребром куба. Получаем, что катеты необходимого треугольника равны 
и a, а гипотенуза равна корню из суммы их квадратов:
