Как найти диагональ квадрата зная радиус окружности

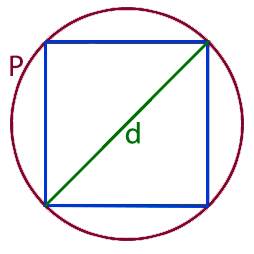
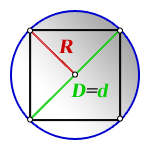
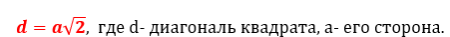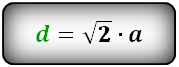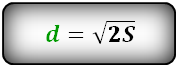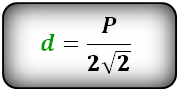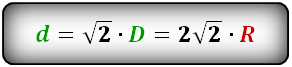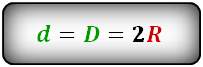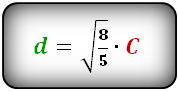           Внимательно прочитаем задание и определим данные, которые нам понадобятся в процессе решения. Нам дан квадрат с вписанной в него окружностью и дан ее радиус. Значит нужно вспомнить  свойства данных фигур и их взаимосвязь с друг другом.

Первый способ решения

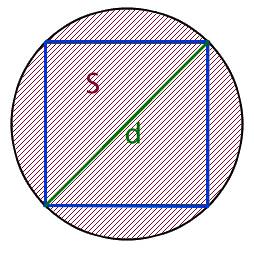
   Первый способ нахождения ответа основывается на формуле диагонали квадрата:

     Зная эту формулу алгоритм наших действий, следующий:

• -найти сторону квадрата;

• – подставить найденное значение в формулу;

• – вычислить;

• – записать ответ. 

А можно ли решить данную задачу иначе? Да, конечно! Для этого рассмотрим другой способ.

Все формулы длины диагонали квадрата

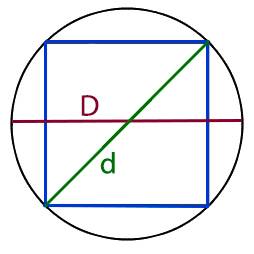
1. Формулы диагонали квадрата через стороны, площадь, периметр

a – сторона квадрата

S – площадь квадрата

P – периметр квадрата

d – диагональ квадрата

Формулы диагонали квадрата, ( d ):

2. Формула диагонали квадрата через радиус вписанной окружности

R – радиус вписанной окружности

D – диаметр вписанной окружности

d – диагональ квадрата

Формула диагонали квадрата, ( d ):

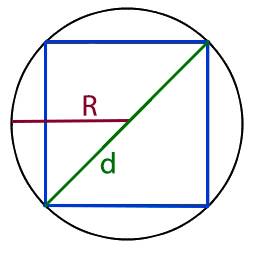
3. Формула диагонали квадрата через радиус описанной окружности

R – радиус описанной окружности

D – диаметр описанной окружности

d – диагональ

Формула диагонали квадрата, ( d ):

4. Формула диагонали квадрата через линию выходящую из угла на середину стороны квадрата

C – линия выходящая из угла на середину стороны квадрата

d – диагональ

Формула диагонали квадрата, ( d ):

Онлайн калькулятор диагонали вписанного в круг квадрата. Как узнать длину диагонали вписанного в круг квадрата.

Вычислить диагональ вписанного квадрата через:

Радиус круга R:

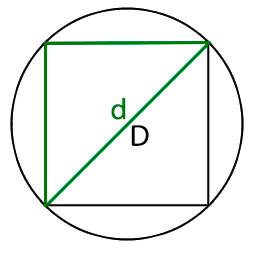
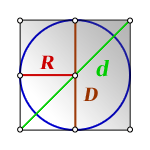
Для того что бы найти диагональ вписанного в круг квадрата, нам необходимо узнать диаметр круга в который вписан квадрат при этом диагональ квадрата (d) и диаметр круга (D) равны.

Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:

1. либо площадь круга, обозначаемая буквой S,
2. либо периметр круга, обозначаемый буквой P,
3. либо радиус круга, обозначаемый буквой R,
4. либо диаметр круга, обозначаемый буквой D.

Теперь для того что бы найти диагональ треугольника (которая равна диаметру) нам необходимо перейти к следующему шагу

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

Соответственно если мы знаем диаметр круга мы знаем и длину диагонали квадрата,

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

[spoiler title=”источники:”]

http://tamali.net/calculator/inscribed/square/diagonal/

http://matworld.ru/geometry/kvadrat.php

[/spoiler]

Квадрат – это четырёхугольник, у которого все стороны и углы раны. Он обладает следующими
свойствами:

• все углы равны между собой и равняются 90;
• смежные стороны перпендикулярны друг другу;
• квадрат имеет только две равные диагонали;
• диагонали в точке пересечения делятся пополам;
• диагонали перпендикулярны друг другу и являются биссектрисами улов квадрата;
• радиус описанной окружности равен половине диагонали квадрата;
• диаметр вписанной окружности равен стороне квадрата.

Через длину стороны

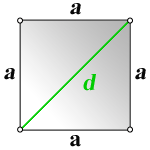
Чтобы найти диагональ квадрата через длину стороны, необходимо значение стороны а умножить на
квадратный корень из двух. Данная формула выводится из теоремы Пифагора для прямоугольных
треугольников, так как диагональ делит квадрат на два прямоугольных треугольника. Сама диагональ
является гипотенузой данных треугольников. Теорема записывается c² = a² + b², и в данном случае вместо c выступает диагональ d, а вместо
b выступает а, так как катеты равны. Преобразуем: d² = a² + a²; d² = a² * 2. Теперь необходимо извлечь квадратный корень:

D = √(a² * 2)

где D – диагональ квадрата, а – длина стороны.

Пример. Необходимо найти диагональ квадрата d, если сторона квадрата a = 10 см.
Необходимая формула: D = √(a² * 2). Вместо а подставляем значение
10: D = √(10² * 2). После того как находим квадратный корень из двух,
производится умножение и получившееся значение округляем до нужного знака после запятой: D ~ 14,14
см.

Через периметр квадрата

Диагональ квадрата равна отношению периметра P квадрата к произведению четырех на квадратный корень
из двух.

D = P / 4√2

где d – диагональ квадрата, S – периметр квадрата

Пример.Необходимо найти диагональ квадрата d, если периметр P = 20 см. Необходимая
формула: D = P / 4√2. Вместо P подставляем значение 20: D = 20 / 4√2.  Получившееся значение округляем до нужного знака после
запятой: D ~ 3,54 см.

Через площадь квадрата

Чтобы найти диагональ квадрата через площадь S, нужно вычислить квадратный корень из произведения S ×
2 . Сама площадь S для прямоугольника имеет формулу S = a * b. Так как
квадрат — это прямоугольник с равными сторонами, формула для площади квадрата S = a². Если
выразить сторону через площадь, формула будет иметь вид: а = √S.

D = √(S * 2)

где D – диагональ квадрата, S – площадь квадрата.

Пример. Необходимо найти диагональ квадрата d, если площадь S = 10 см². Необходимая
формула: D = √(S * 2) Вместо S подставляем значение 10: D = √(10 * 2).  Получившееся значение округляем до нужного знака после
запятой: D ~ 4,47 см.

Через диаметр вписанной окружности

Диагональ квадрата равна произведению диаметра вписанной окружности D на квадратный корень из
двух.

D = d * √2

где D – диагональ квадрата, d – диаметр вписанной окружности.

Пример. Необходимо найти диагональ квадрата d, если диаметр вписанной окружности d =
10 см. Необходимая формула: D = d * √2. Вместо R подставляем значение 10:
d = 10 * √2. Диагональ равна 14,14 см.

Диагональ квадрата через диаметр описанной окружности

Диагональ квадрата равна диаметру d описанной окружности.

D = d

где D – диагональ квадрата, d – радиус описанной окружности.

Пример. Необходимо найти диагональ квадрата d, если диаметр описанной окружности d =
10 см. Необходимая формула: d = D. Вместо d подставляем значение
10. Диагональ равна 10 см.

Через радиус описанной окружности

Диагональ квадрата равна радиусу описанной окружности, умноженному на два.

D = 2R

где D – диагональ квадрата, R – радиус описанной окружности.

Пример. Необходимо найти диагональ квадрата D, если радиус описанной окружности R =
10 см. Необходимая формула: Вместо R подставляем значение 10: D = 2 * 10.
Получившееся значение округляем до нужного знака после запятой: D = 20 см.

Через радиус вписанной окружности

Диагональ квадрата равна произведению удвоенного радиуса вписанной окружности R на квадратный корень
из двух.

D = 2R√2

где D – диагональ квадрата, R– радиус вписанной окружности.

Пример. Необходимо найти диагональ квадрата D, если радиус описанной окружности D =
10 см. Необходимая формула: D = 2R√2. Вместо R подставляем значение 10:
d = 2 * 10 * √2. Диагональ равна 28,28 см.

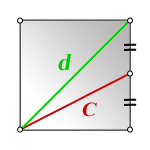
Через линию, которая выходит из угла на середину стороны квадрата

Диагональ квадрата равна произведению квадратного корня из восьми пятых и линии C, выходящей из угла
на середину стороны квадрата.

D = √(8/5) * C

где D – диагональ квадрата, C – линия, выходящая из угла на середину квадрата.

Пример. Необходимо найти диагональ квадрата D, если линия, которая проходит из угла
на середину стороны квадрата С = 10 см. Необходимая формула: D = √(8/5) * C. Вместо R подставляем значение 10: D = √(8/5) * 10. Диагональ
равна 12,64 см.

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Округление:

* – обязательно заполнить

Радиус вписанной окружности (R1) = 10

Cторона, диаметр вписанной окружности (L) = (R1*2) = (10*2) = 28.28

Диагональ, диаметр описанной окружности (M) = (2*L^{2}) = (2*20^{2}) = 20

Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{28.28}{2}) = 14.14

Периметр (P) = (L*4) = (20*4) = 80

Площадь (S) = (L^{2}) = (20^{2}) = 400