Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие страницы
- 📢 Поделиться и комментировать
Что такое диаметр круга?
Диаметр круга – это отрезок, соединяющий две точки на окружности и проходящий через центр круга.
Если же говорить, про другие фигуры, то диаметром называется максимальное расстояние между точками этой фигуры. Диаметр круга – не исключение, так как это самый длинный отрезок, который можно провести в границах окружности.
Если нарисовать диаметр, то он будет выглядеть следующим образом (выделен красным на рисунке ниже).
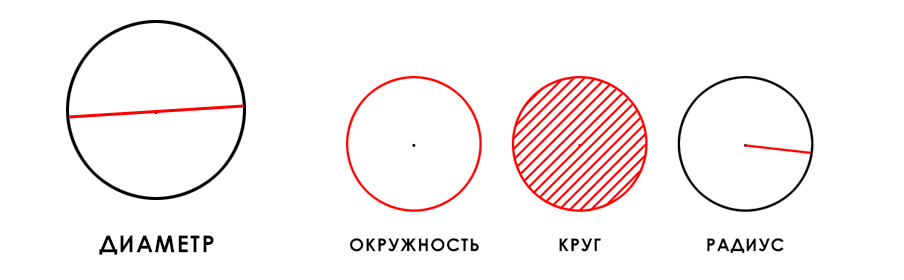
Теперь давайте рассмотрим, как можно найти диаметр и какие для этого существуют формулы.
Формулы определения диаметра круга
Для определения диаметра существует несколько разных способов в зависимости от известных частей круга.
По радиусу
Самая простая формула определения диаметра может быть использована, если известен радиус круга. Радиус — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности. Диаметр равен двум радиусам.
d = r × 2
Где d – это диаметр, а r – радиус.
По длине окружности
Второй способ нахождения диаметра можно использовать тогда, когда известна длина окружности. Окружность — это замкнутая плоская кривая, все точки которой равноудалены от центра. Тако вот, диаметр равен длине окружности, делённой на число Пи.
d = L / π
Где d – это диаметр, а L – длина окружности, а π – константа, равная 3,14.
Эта формула, основывает на том, что отношение длины окружности к её диаметру всегда является постоянным числом, которое равняется примерно 3,14 и называется π (пи).
Через площадь круга
Чуть более изощренной и сложной является формула вычисления диаметра через площадь круга. Чаще всего требуется, наоборот, посчитать площадь круга, если известен диметр. Но если задача стоит обратная, то формула расчёта будет выглядеть следующим образом:
d = 2 × (S/π)1/2
Где d – диаметр, S – площадь круга, а π – константа, которая примерно равна 3,14.
То есть диаметр равен удвоенному корню частного площади круга к числу пи. Стоит отметить, что корень и степень ½ – это одно и то же.
Примеры вычисления диаметра
Давайте для закрепления рассмотрим несколько примеров.
Пример 1. Диаметр по длине окружности трубы 🚿
Предположим, у вас под рукой не оказалось штангенциркуля (устройства для измерения ширины изделий).

А вам требуется рассчитать диаметр действующей трубы, конца которой не видно. Для этого с помощью рулетки или сантиметра, вы можете измерить длину окружности, просто обернув рулетку вокруг трубы. А потом эту длину нужно будет разделить на 3,14. Если длина окружности трубы оказалась 31,4 сантиметра, тогда диаметр будет равен частному этой длинны к числу Пи, то есть:
d = 31,4 / 3,14 = 10 см.
Это и есть правильный ответ – 10 сантиметров.
Пример 2. Диаметр по колеса радиусу 🚲
Тут всё гораздо проще. Предположим, что вы знаете радиус колеса велосипеда – 10 дюймов. Какой будет диаметр?
Диаметру будет равен двум радиусам, то есть 20 дюймов.
Кстати, для справки, 1 дюйм = 2,54 сантиметра. То есть 10 дюймов = 25,4 сантиметра. В итоге диаметр колеса равен: 2 × 25,4 = 50,8 см.
❓Вопросы и ответы
И конечно же обратите внимание на ответы на часто задаваемые вопросы относительно расчёта длины диаметра круга.
Как работает ваш онлайн-калькулятор?
Просто. Вы выбираете, что известно: радиус, длина окружности или площадь круга (1), затем вписываете известное значение (2), выбираете размерность из мм, см, м, км (3) и нажимаете кнопку «рассчитать»?
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть различные калькуляторы, в частности калькуляторы: площади круга, длины окружности и диаметра. Для последнего калькулятор находится на данной странице.
Достаточно ли у меня данных для расчёта?
Для вычисления диаметра круга нужно что-то одно: радиус, длина окружности или площадь круга. Остальное вычислит наш калькулятор по специальным формулам, которые описаны выше.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Если у автомобильного колеса параметр R16, то какой у него диаметр?
16 дюймов, а радиус 8 дюймов. Как ни странно, диаметр такого колеса (точнее диска колеса) составляет 16 дюймов, то есть 40,64 см. Очень часто люди называют радиус в качестве единицы измерения: мол, радиус 16 дюймов. Но тогда представьте, для какого трактора диаметр диска будет более 80 сантиметров.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Как посчитать диаметр окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать диаметр окружности
Чтобы посчитать диаметр окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
 Для того чтобы вычислить диаметр окружности вам необходимо знать её радиус, либо длину окружности, либо её площадь. Если вы знаете хотя бы один из этих параметров, введите его в соответствующие поле и узнаете, чему равен диаметр окружности.
Для того чтобы вычислить диаметр окружности вам необходимо знать её радиус, либо длину окружности, либо её площадь. Если вы знаете хотя бы один из этих параметров, введите его в соответствующие поле и узнаете, чему равен диаметр окружности.
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Ответ:
0
Каков диаметр (d) если длина окружности C?
Формула
d = C/π, где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
её радиус ?
Ответ:
0
Каков диаметр окружности (d) если её радиус r?
Формула
d = 2⋅r
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
её площадь ?
Ответ:
0
Каков диаметр окружности (d) если её площадь S?
Формула
d = √4S/π, где π ≈ 3.14
Пример
Если площадь круга равна 5 см2, то его диаметр примерно равен 2.52 см.
См. также
При помощи нашего калькулятора вы легко сможете узнать диаметр круга или окружности.
Для того что бы вычислить диаметр круга необходимо знать его длину или площадь. Если нам известа одна из указаннх величин, для нас не составит труда вычислить диаметр круга.
Диаметр круга рассчитывается по следующим формулам:
- Если нам известна длина:
Формула для расчета диаметра круга через его длину:
D=P/π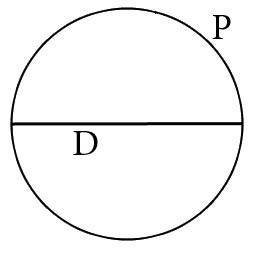
- Если нам известна площадь:
Формула для расчета диаметр круга через площадь:
D=2√
S/π
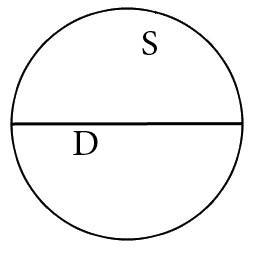
- Если нам известен диаметр:
Формула для расчета диаметр круга через радиус:
D=2R
Где D – диаметр круга, S – площадь круга, P – длина круга, R – радиус, π – число Пи которое всегда примерно равно 3,14.
Информация по назначению калькулятора
В евклидовой геометрии круг – это множество всех точек на плоскости на фиксированном расстоянии, называемом радиусом, от заданной точки, центра. Длина круга называется его окружностью, а любая непрерывная часть окружности называется дугой.
Окружность – это простая замкнутая кривая, которая делит плоскость на внутреннюю и внешнюю. Внутренняя часть круга называется диском. Математически круг можно понимать и несколькими другими способами. Например, это частный случай эллипса, в котором два фокуса совпадают (то есть они являются одной и той же точкой). Альтернативно, окружность можно рассматривать как коническое сечение, достигаемое, когда прямой круговой конус пересекается плоскостью, перпендикулярной оси конуса.
Число π (ПИ) равно 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375…
Все круги обладают одинаковыми свойствами. Некоторые из них отмечены далее:
⇒ Для любого круга заключенная площадь и квадрат его радиуса находятся в фиксированной пропорции, равной математической константе π (ПИ).
⇒ Для любого круга длина окружности и радиус находятся в фиксированной пропорции, равной 2π.
⇒ Круг – это фигура с наибольшей площадью для заданной длины периметра.
⇒ Круг имеет очень симметричную форму. Каждая линия, проходящая через центр, образует линию симметрии отражения. Кроме того, существует вращательная симметрия вокруг центра для каждого угла.
⇒ Окружность с центром в начале координат радиусом 1 называется единичной окружностью.
Онлайн калькулятор поможет найти параметры круга, такие как:
- Диаметр
- Радиус
- Длина окружности
- Площадь
– равен двум радиусам или длине окружности поделенной на число π (d=r*2=P/π)
– равен половине диаметра или длине окружности поделенной на 2π (r=d/2=P/2π)
– (или периметр круга) равна диаметру умноженному на число π (P=d*π=2π*r)
– равна радиусу в квадрате умноженному на число π (S=πr2=¼πd2)
|
Нахождение радиуса и диаметра по площади круга. Как найти радиус и диаметр окружности, если известна площадь круга? Площадь круга вычисляется по формуле S=Пи*R^2, где R – радиус круга, а Пи – трансцендентная величина приблизительно равная 3,14 с недостатком, и равная 3,15 с избытком. Тогда средняя величина Пи=6.29/2=3,145, более точно Пи=3,14159… R=√(S/Пи), диаметр D=2*R=2*√(S/Пи). Например, при S=10 квадратных единиц R=√(10/Пи)=3,183…, а D=6,366… . автор вопроса выбрал этот ответ лучшим Corelpainter 3 года назад Площадь круга мы можем вычислить по формуле, которая представлена ниже, где латинской буквой S обозначается площадь, буквой R – радиус, а π – является иррациональным числом равное 3,14159265358979323846… Для использования в школьных расчётах число π округляется до второго знака после запятой, то есть 3,14 S = πR² или S = 3,14R² Если в задании нам известна площадь круга то мы можем легко вычислить радиус по формуле: R = √(S / π) или R = √(S / 3,14) Чтобы вычислить диаметр круга нужно просто результат (радиус) умножить на 2: D = 2√(S / π) или D = 2√(S / 3,14)
Для того, чтобы вычислить площадь круга, необходимо знать формулу S=πR², где S – это площадь круга, π – число Пи ( 3,1415926535…, его обычно для вычислений округляют до 3,14 ), R – радиус круга. Из этой формулы можно вывести формулу для вычисления радиуса круга через его площадь: R=√S/π. Для того, чтобы вычислить радиус круга нужно извлечь корень квадратный ( √ ) из частного : площади круга, поделенной на число Пи. Рассмотрим конкретный пример вычисления радиуса круга через его площадь: Площадь круга равна 10 кв.см., найдем радиус круга: R=√10/3,14=1,78 см. Радиус круга, площадь которого равна 10 кв.см., равен 1,78 см. Радиус круга равен половине его диаметра, то есть D=2R, где D – диаметр круга, а R – его радиус. Если в эту формулу подставить формулу радиуса круга через его площадь, то получим такую формулу для вычисления диаметра круга через его площадь: D=2√S/π. То есть, для того, чтобы вычислить диаметр круга нужно извлечь корень квадратный ( √ ) из частного: площади круга, поделенной на число Пи, и полученный результат умножить на два. Если мы вычислим диаметр круга с площадью 10 кв.см. по этой формуле, то получим результат 3,56 см.
Ксарфакс 5 лет назад Для того, чтобы найти радиус и диаметр окружности через площадь круга, нужно: 1) Выразить радиус из формулы площади круга. C = πR². Здесь C – площадь круга, R – радиус, π – число Пи (оно равно 3,14). R² = C / π. R = √(C / π). Таким образом, если известна площадь круга, то для нахождения радиуса нужно площадь разделить на Пи и извлечь из полученного значения квадратный корень. 2) Выразить диаметр через радиус. D = 2R. Диаметр окружности всегда в два раза больше, чем радиус. _ Другой вариант записи: D = 2√(C / π). Пример Известна площадь круга C = 13,5. Нужно найти, чему равен радиус и диаметр окружности. R ≈ √ (13,5 / 3,14) ≈ √4,3 ≈ 2,07. D = 2R = 4,14. Таким образом: Если площадь круга равна 13,5, то радиус равен 2,07 и диаметр равен 4,14.
Simple Ein 3 года назад Если в задаче известна площадь круга легко узнать радиус и диаметр круга. Радиус круга – отрезок, соединяющий центр окружности с любой точкой, которая лежит на линии окружности. Диаметр окружности (круга) состоит из двух радиусов. Т.е. значение радиуса окружности необходимо умножить на 2, чтобы узнать диаметр. Необходимо вспомнить формулу площади круга. Площадь окружности равна произведению числа «Пи» на квадрат радиуса окружности. Чтобы найти радиус окружности необходимо площадь окружности разделить на число «Пи», затем из частного извлечь корень.
Алиса в Стране 3 года назад Чаще в задачках мы площадь круга находим через его радиус или диаметр, есть вот такая формула: C = πR², площадь равна произведению числа пи на квадрат радиуса, это формула одна из немногих, которые я до сих пор помню. Квадрат радиуса, значит, равен площадь умноженная на число пи, а сам радиус равен корню квадратному, извлеченному из этого произведения: R = √(C / π). Диаметр, ну уж это то все точно помнят, равен двум радиусам. Ну теперь давайте решим эту простенькую задачку с конкретными цифрами. Пусть площадь круга равна 28,26 см². тогда радиус равен корню квадратному из 28,26/3,14, то есть корню квадратному из девяти, радиус окружности равен трем сантиметрам, диаметр – шести сантиметрам.
Площадь круга делите на число Пи (3,14) и из результата этого деления извлекайте квадратный корень. Получаете радиус окружности. Ну а найти диаметр по известному радиусу это для 2 класса – умножить на 2. Для нахождения радиуса и диаметра окружности через площадь круга вам потребуется вычислить. Извлеките квадратный корень из частного, а именно площади круга, которая была поделена на число Пи. Так воспользясь формулой: S=πR² мы поймем, что S является площадью. π – 3,1415926535. Например: Евгений трохов 5 лет назад Можно привести и такой вариант.S(площадь круга)=nd^2/4 (п-число пи,d-диаметр).Отсюда d=Корень квадратный из (4S/n).Ну а чтобы найти радиус надо диаметр разделить пополам.Ну а число “пи” сами возьмёте с необходимой вам точностью. Площадь круга вычисляется по формуле S=ПиR в квадрате, где Пи – постоянная величина, равная 3,14, а значит, чтобы найти радиус, нужно площадь разделить на число Пи и извлечь из этого числа корень. Ну а диаметр – это 2 радиуса. Знаете ответ? |

