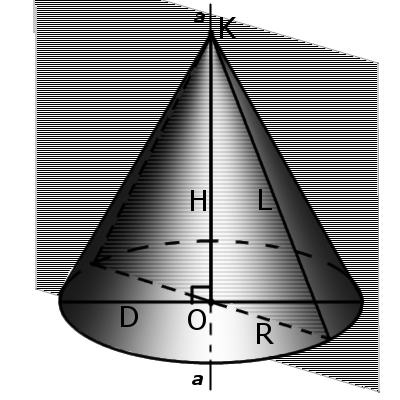
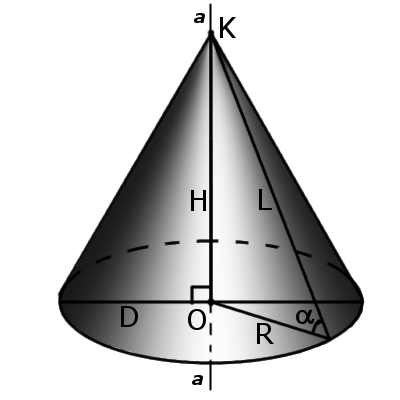
Прямой конус – это конус, у которого ось перпендикулярна основанию. У такого конуса ось совпадает с высотой, а все образующие равны между собой
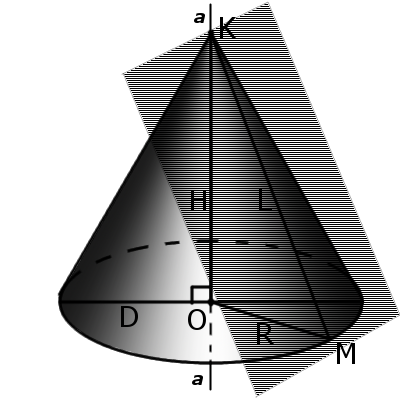
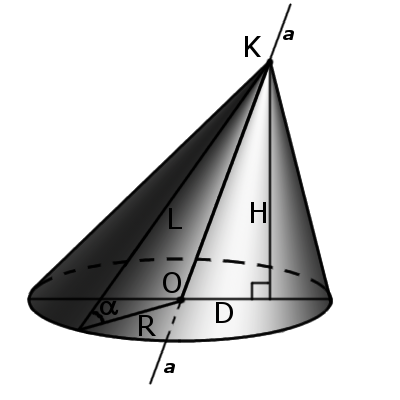
Косой (наклонный) конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой
Образующая конуса – это отрезок, который соединяет вершину конуса с границей основания конуса.
Длина образующей, L
$$
L = sqrt{R^2 + h^2}
$$
Площадь основания, SО
$$
S_О = pi * R^2
$$
Площадь боковой поверхности, SБ
$$
S_Б = pi * R * L
$$
Общая площадь поверхности, S
$$
S = pi * R * L + pi * R^2 = S_О + S_Б
$$
Объём прямого конуса, V
$$
V = {1 over 3} * pi * h * R^2
$$
Объём любого конуса
$$
V = {1 over 3} * S_О * h
$$
Угол ∠ f для развертки
$$
∠ f = 360° * {R over L}
$$
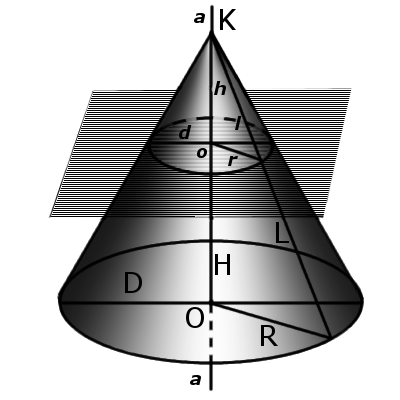
Элементы конуса
Определение. Вершина конуса – это точка (K), из которой исходят лучи.
Определение. Основание конуса – это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.
Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):
L2 = R2 + H2
Определение. Направляющая конуса – это кривая, которая описывает контур основания конуса.
Определение. Боковая поверхность конуса – это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.
Определение. Высота конуса (H) – это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
Определение. Ось конуса (a) – это прямая, проходящая через вершину конуса и центр основания конуса.
Определение. Конусность (С) конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса – это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:
где C – конусность, D – диаметр основания, d – диаметр меньшего основания и h – расстояние между основаниями.
Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:
где R – радиус основы, а H – высота конуса.
Определение. Осевое сечение конуса – это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника – это диаметр основания конуса.
Определение. Касательная плоскость к конусу – это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.
Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).
Определение. Прямой конус – это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Формула. Объём кругового конуса:
где R – радиус основы, а H – высота конуса.
Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:
Sb = πRL
Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:
Sp = πRL + πR2
Определение. Косой (наклонный) конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.
Формула. Объём любого конуса:
где S – площадь основы, а H – высота конуса.
Определение. Усеченный конус – это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.
Формула. Объём усеченного конуса:
где S1 и S2 – площади меньшей и большей основы соответственно, а H и h – расстояние от вершины конуса до центра нижней и верхней основы соответственно.
Уравнение конуса
1. Уравнение прямого кругового конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | – | z2 | = 0 |
| a2 | a2 | c2 |
2. Уравнение прямого эллиптического конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | = | z2 |
| a2 | b2 | c2 |
Основные свойства кругового конуса
1. Все образующие прямого кругового конуса равны между собой.
2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.
4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).
7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 ноября 2022 года; проверки требуют 2 правки.
У этого термина существуют и другие значения, см. Конус (значения).
Ко́нус (через нем. Konus и лат. cōnus, от др.-греч. κώνος[1] — «сосновая шишка»[2]) — поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса)[3].
Если направляющая конуса — замкнутая кривая, то коническая поверхность служит границей пространственного тела, которое также называют «конусом» (см. рисунок), а внутренность этой кривой называют «основанием конуса», если основание конуса представляет собой многоугольник, такой конус является пирамидой.
Иногда вместо лучей рассматривают прямые, тогда получается двойной конус, состоящий из двух симметричных относительно вершины частей.
Конус и связанные с ним конические сечения играют большую роль в математике, астрономии и других науках.
Связанные определения[править | править код]
- Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
- Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
- Конусность — соотношение высоты и диаметра основания конуса.
Типы конусов[править | править код]
-
Прямой круговой конус
-
Прямой и косой круговые конусы с равным основанием и высотой: их объём одинаков
-
Усечённый прямой круговой конус
- Прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
- Косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
- Круговой конус — конус, основание которого является кругом.
- Конус вращения, или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
- Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.
- Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
- Равносторонний конус — конус вращения, образующая которого равна диаметру основания [4].
Свойства[править | править код]
- Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.
-
- где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
- Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
- Телесный угол при вершине прямого кругового конуса равен
-
- где α — угол раствора конуса.
- Площадь боковой поверхности прямого кругового конуса равна
-
- а в общем случае
- где R — радиус основания,
— длина образующей,
— длина границы основания.
- Полная площадь поверхности (то есть сумма площадей боковой поверхности и основания) равна
- для прямого кругового конуса и
- для произвольного, где
— площадь основания.
- Объём кругового (не обязательно прямого) конуса равен
- Для усечённого кругового конуса (не обязательно прямого) объём равен:
-
- где
и
— радиусы соответственно нижнего и верхнего оснований,
— высота от плоскости нижнего основания,до верхнего основания.
- Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:
-
- где
и
— площади соответственно верхнего (ближнего к вершине) и нижнего оснований,
и
— расстояния от плоскости соответственно верхнего и нижнего основания до вершины.
- Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).
Уравнение прямого кругового конуса[править | править код]
Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:
- В сферической системе координат с координатами (r, φ, θ):
- В цилиндрической системе координат с координатами (r, φ, z):
-
или
- В декартовой системе координат с координатами (x, y, z):
-
- Это уравнение в каноническом виде записывается как
- где константы a, с определяются пропорцией
Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид
- причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением
где функция
является однородной, то есть удовлетворяющей условию
для любого действительного числа α.
Развёртка[править | править код]
Развёртка прямого кругового конуса
Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.
В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора 
- φ = 360°·(r/l).
Вариации и обобщения[править | править код]
См. также[править | править код]
- Коническая поверхность
- Коническое сечение
- Конус (топология)
- Световой конус
Примечания[править | править код]
- ↑ Этимологический словарь русского языка Макса Фасмера
- ↑ «I κῶνος»
- ↑ Математический энциклопедический словарь, 1988, с. 288.
- ↑ Математический справочник. Дата обращения: 22 мая 2020. Архивировано 2 декабря 2020 года.
Литература[править | править код]
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд. — М.: Наука, 1970. — 720 с.
- Конус // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 288. — 847 с.
Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.
Треугольник (POA) вращается вокруг стороны (PO).
(PO) — ось конуса и высота конуса.
(P) — вершина конуса.
(PA) — образующая конуса.
Круг с центром (O) — основание конуса.
(AO) — радиус основания конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось (PO) конуса.
Осевое сечение конуса — это равнобедренный треугольник.
(APB) — осевое сечение конуса.
— углы между образующими и основанием конуса.
Для конуса построим развёртку боковой поверхности. Это круговой сектор.

Сектор имеет длину дуги, равную длине окружности в основании конуса
2πR
, угол развёртки боковой поверхности
α
.
В конусе нельзя обозначить угол развёртки.
На развёртке конуса нельзя обозначить высоту и радиус конуса.
Образующая конуса (l) является радиусом сектора.
Таким образом, боковая поверхность конуса является частью полного круга с радиусом (l):
Длина дуги также является частью длины полной окружности с радиусом (l), но в то же время длина дуги — это длина окружности основания конуса с радиусом (R).
Сравним выражения длины дуги и выразим
α
через (R):
2πl⋅α360°=2πR;α=2πR⋅360°2πl=R⋅360°l.
Получаем ещё одну формулу боковой поверхности конуса; не используется угол развёртки боковой поверхности:
.
Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.
Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.
— ось конуса и высота конуса.
Круги с центрами (O) и
O1
— основания усечённого конуса.
(AO) и
A1O1
— радиусы оснований конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось
OO1
конуса.
Осевое сечение конуса — это равнобедренная трапеция.
— осевое сечение конуса.
Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:
Sбок.=πR⋅PA−πr⋅PA1=πR⋅PA1+AA1−πr⋅PA1==πR⋅PA1+πR⋅AA1−πr⋅PA1==πR⋅l+πR−πr⋅PA1.
Так как
ΔPAO∼ΔPA1O1
, то стороны их пропорциональны:
PAPA1=Rr;l+PA1PA1=Rr;r⋅l+PA1=R⋅PA1;rl=R⋅PA1−r⋅PA1;PA1⋅R−r=rl;PA1=rlR−r.
Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:
Sбок.=πRl+π⋅PA1⋅R−r=πRl+π⋅rlR−r⋅R−r;Sбок.=πRl+πrl=πl⋅R+r.
Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.
Круглый прямой конус
В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая – директрисой, или направляющей.
Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.
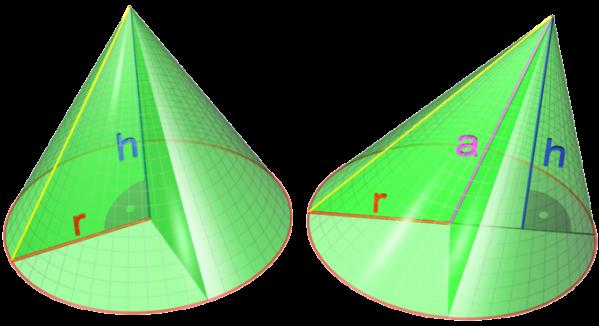
Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.
Здесь r – радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.
Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая – это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.
Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.
Вычисление диаметра фигуры через линейные параметры и угол при основании
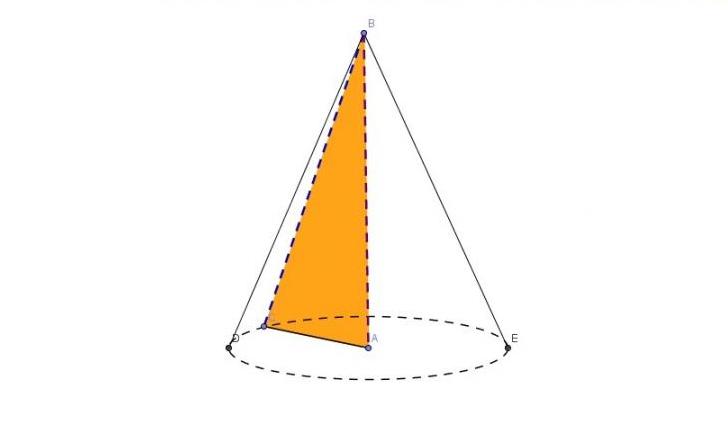
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g – это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
d = 2*√(g2 – h2)
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
d = 2*g*cos(φ);
d = 2*h/tg(φ)
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Вычисление диаметра через площадь поверхности и генератрису
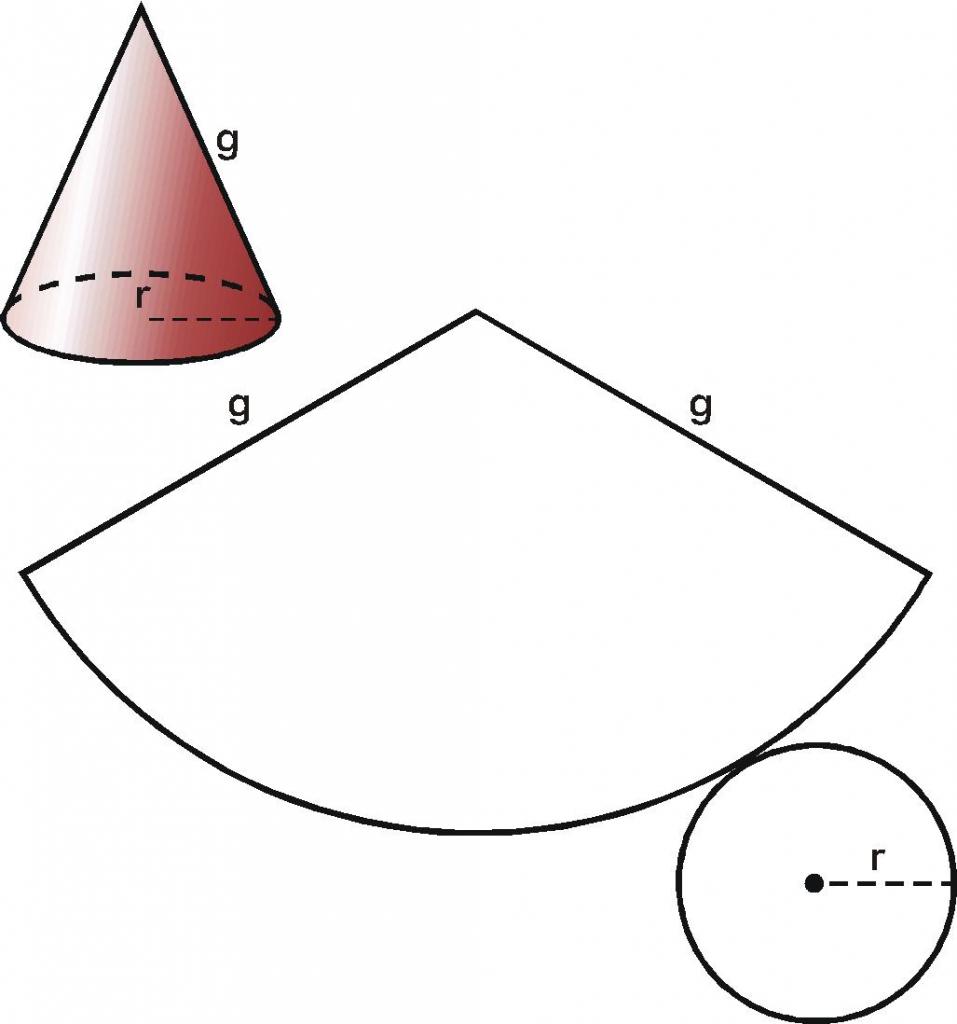
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.
Общая площадь развертки определяется по следующей формуле:
S = pi*r2 + pi*r*g
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Определение диаметра через объем и высоту
Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
V = 1/3*S*h
Здесь S – площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
V = 1/3*pi*r2*h
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
r = √(3*V/(pi*h));
d = 2*r = 2*√(3*V/(pi*h))
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Задача на определение диаметра через известную площадь конуса и его образующую
Дан конус, площадь поверхности которого составляет 150 см2. Генератриса равна 14 см. Чему равен диаметр конуса?
Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:
S = pi*r2 + pi*r*g =>
r2 + 14*r – 150/3,14 = 0
При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:
D = 142 – 4*1*(-150/3,14) = 387,0828
Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:
r = (-14±√D)/2
Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:
r = (-14+√387,0828)/2 = 2,837 см
Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.
В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.