Главная › ЕГЭ. Стереометрия
В правильной четырехугольной пирамиде найти диагональ основания
Автор: Ирина Гайкова
Комментариев нет
447
Telegram
VK
OK
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SD = 10, SO = 6. Найдите длину отрезка AС.
Интересная статья? Поделитесь ею пожалуйста с другими:

Хотите обучаться математике индивидуально?
Запишитесь на консультацию.
Мы храним ваши данные в тайне
Похожие записи:
-
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб
-
Если каждое ребро куба увеличить на 1, то его площадь поверхности
-
В правильной треугольной пирамиде найти высоту боковой грани
Оставьте свой комментарий:
- на Блоге
- в Вконтакте
- в Фейсбук









 Еще смайлы
Еще смайлы
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий
Имя *
Email *
Вебсайт
Получать новые комментарии по электронной почте. Вы можете подписаться без комментирования.
Нажимая на кнопку “Отправить комментарий”, я соглашаюсь с политикой обработки персональных данных
как найти диагональ основания четырехугольной пирамиды?
Ангелина Вернер
Ученик
(110),
на голосовании
10 лет назад
Дополнен 10 лет назад
Правильная четырехугольная пирамида SABCD ,
О-центр основания, S-вершина SO=4,SC=5 Найти длину отрезка AC
как я поняла это диагональ основания
Голосование за лучший ответ
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. В задачах вместо символа “квадратный корень” применяется функция sqrt(), в которой sqrt – символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак “√”.
Задача.
Диагональ основания правильной четырехугольной пирамиды равна 4 см, а боковая грань образует с основанием угол 60 градусов. найдите объем пирамиды.
Решение.
Объем пирамиды найдем по формуле:
V=1/3 Sh
Зная диагональ основания пирамиды, найдем сторону основания.
d2 = a2 + a2
42 = 2a2
16 = 2a2
a= √8 = 2√2
Соответственно, площадь основания
S = 8 см2 .
Проведем через вершину правильной четырехугольной пирамиды вертикальное сечение. Поскольку боковые грани пирамиды наклонены к основанию под углом 60 градусов, то сечение образует равносторонний треугольник.
Основание равностороннего треугольника равно 2√2. Откуда высота будет равна
h = √3/2 a
h = √3/2 * 2√2 = √6
Откуда объем правильной пирамиды с четырехугольником в основании равен
V=1/3 Sh
V = 1/3 * 8 * √6 = 8√6 / 3
Ответ: 8√6 / 3 см3.
Задача.
Сторона основания правильной четырехугольной пирамиды равна а. Двугранные углы при основании равны
α. Найти площадь полной поверхности пирамиды.
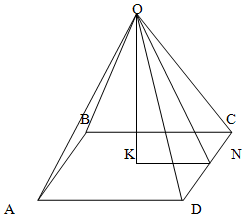
Решение.
Поскольку пирамида правильная, то ее высота проецируется в центр основания.
Значит KN = a/2
Соответственно, треугольник OKN – прямоугольный. Значит
ON = KN / cos α = a / 2cos α
Поскольку пирамида правильная, то треугольник DOC – равнобедренный. Значит его площадь равна
Sт = DC * ON / 2
Sт = ( a * a / 2cos
α) / 2 = a2 / 4cos α
Откуда площадь боковой поверхности правильной пирамиды будет равна площади всех ее боковых граней
Sб = 4a2 / 4cos
α
Sб = a2 / cos α
Откуда площадь полной поверхности равна
Sп = a2 / cos
α + a2 = a2 ( 1 + 1 / cos α )
Ответ: площадь полной поверхности правильной четырехугольной пирамиды равна a2 ( 1 + 1 / cos α )
0
Правильная пирамида с четырехугольником в основании |
Описание курса
| Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании
Геометрическая фигура пирамида: описание, основные виды, свойства, формулы
Содержание:
- Что такое пирамида в геометрии
- Виды пирамид
-
Свойства пирамиды
- Свойства правильной пирамиды
- Формулы вычисления объема и площади
Что такое пирамида в геометрии
Пирамидой называют многогранную объемную фигуру, которая ограничена плоским многоугольником в виде основы и треугольниками с общей вершиной, находящейся за пределами плоскости основания.
Боковой гранью пирамиды является треугольник, у которого один из углов лежит на вершине этой геометрической фигуры, а противоположная ему сторона соответствует стороне основания. Общие стороны, которыми обладают боковые грани, называются боковыми ребрами. Их количество в пирамиде соответствует числу углов многоугольника.
Высота пирамиды является перпендикуляром, который опустили из вершины к основанию пирамиды.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Перпендикуляр боковой грани пирамиды, который опустили из ее вершины на сторону основания, называют апофемой.
Диагональным сечением пирамиды называют сечение данной геометрической фигуры, которое пролегает через ее вершину и диагональ основания.
Построить геометрическую фигуру в виде пирамиды можно с помощью поэтапных действий:
- Нарисовать основание.
- Найти проекцию вершины геометрической фигуры на плоскости ее основания, исходя из условий задачи.
- Провести вертикальную высоту.
- Построить ребра геометрической фигуры.
На рисунке представлена пирамида с четырьмя углами SABCD. В первую очередь следует записывать вершину пирамиды. В основании лежит четырехугольник ABCD. Вершина изображенного многоугольника проецируется в точку О, где пересекаются диагонали. Данная точка представляет собой основание высоты или проекцию вершины. SA, SB, SC, SD представляют собой ребра пирамиды, а отрезки AB, BC, CD, DA являются сторонами ее основания.
Виды пирамид
Основными видами пирамид, которые наиболее часто встречаются при решении задач, являются:
- правильные пирамиды с вершиной, которая спроецирована в центральную точку основания фигуры;
- пирамида с вершиной, спроецированной в центральную точку окружности, которая вписана в геометрическую фигуру;
- пирамида с вершиной, спроецированной в центральную точку окружности, которая описана вокруг геометрической фигуры;
- пирамида с высотой, равной боковому ребру;
- пирамида, высота которой совпадает с высотой боковой грани этого многоугольника.
Свойства пирамиды
Среди свойств, которыми обладает многоугольник в виде пирамиды, можно отметить следующие:
- В случае равенства всех боковых ребер фигуры вокруг ее основания можно описать круг, центр которого совпадет с центром основания пирамиды. Кроме того, через эту точку пройдет перпендикуляр, который опустили из вершины многоугольника.
- Равенство всех ребер пирамиды говорит о том, что они расположены под равными углами к плоскости основания.
- Равенство боковых ребер будет соблюдаться в том случае, когда ими образованы равные углы с плоскостью основания, либо имеется возможность описать вокруг основания многоугольника круг.
- При наклоне боковых граней к плоскости основания под одинаковым углом можно вписать круг в основание пирамиды. При этом проекция вершины пирамиды будет совпадать с центральной точкой данной окружности.
- Равенство апофем боковых граней пирамиды возможно в том случае, когда углы наклона боковых граней к основанию равны.
Свойства правильной пирамиды
Правильную пирамиду характеризуют следующие особенности:
- вершина такой геометрической фигуры расположена на одинаковом расстоянии от всех углов основания;
- равенство всех боковых ребер;
- равенство углов наклона всех боковых ребер к плоскости основания;
- равенство апофем всех боковых граней;
- равенство площадей, которыми обладают все боковые грани;
- для всех граней характерно наличие одинаковых двугранных или плоских углов;
- вокруг такой пирамиды можно описать сферу, центром которой будет являться точка пересечения перпендикуляров, пересекающих середину ребер геометрической фигуры;
- в данный многоугольник можно вписать сферу с центром в точке, в которой пересекаются биссектрисы, выходящие из угла, разделяющего ребро и основание;
- при совпадении центра вписанной сферы с центральной точкой описанной сферы сумма плоских углов при вершине равна π (числу «пи», или 180-ти градусам), или наоборот, один угол соответствует π/n, где n является количеством углов в основании пирамиды.
Формулы вычисления объема и площади
Боковая поверхность пирамиды представляет собой общую площадь всех боковых граней данного многоугольника. Для расчета полной поверхности пирамиды необходимо определить сумму площадей боковой поверхности и основания многоугольника.
Площадь боковой поверхности правильной пирамиды можно рассчитать по формуле, зная периметр основания и апофему:
(Sb = 1/2 ph)
Объем данной геометрической фигуры определяют с помощью площади и высоты:
(V = 1/3 *SоснН)
Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
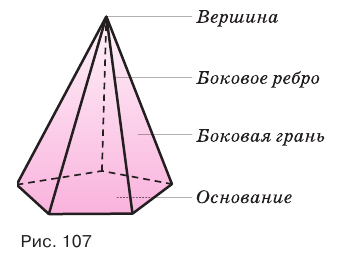
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота 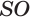
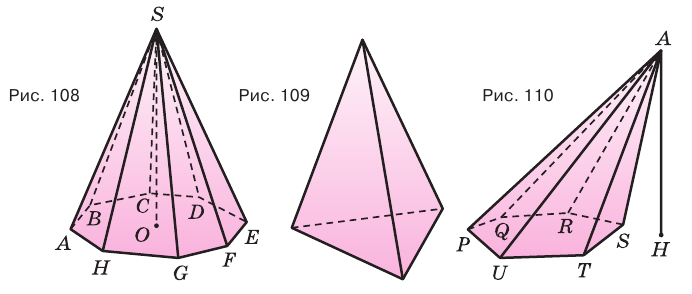
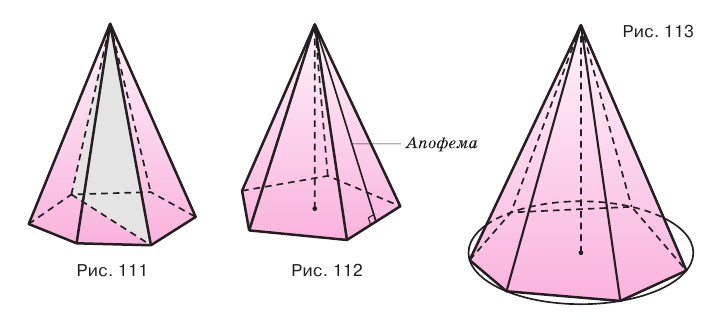
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
- боковые ребра равны;
- боковые грани равны;
- апофемы, равны;
- двугранные углы при основании равны;
- двугранные углы при боковых ребрах равны;
- каждая точка высоты равноудалена от вершин основания;
- каждая точка высоты равноудалена от ребер основания;
- каждая точка высоты равноудалена от боковых граней.
Отметим, что если в пирамиде равны все:
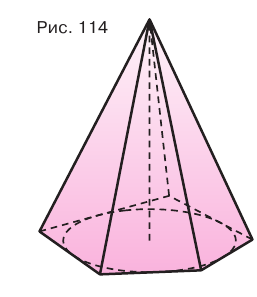
- боковые ребра, то около ее основания можно описать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 113);
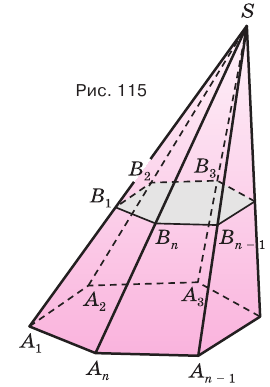
- двугранные углы при основании, то в это основание можно вписать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 114).
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
Теорема 1.
Если пирамиду пересечь плоскостью, параллельной основанию, то:
- а) боковые ребра и высота разделяются на пропорциональные части;
- б) в сечении получается многоугольник, подобный основанию;
- в) площади сечения и основания относятся как квадраты их расстояний от вершины пирамиды.
Используя рисунок 115, докажите эту теорему самостоятельно.
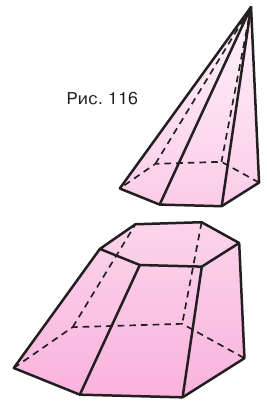
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
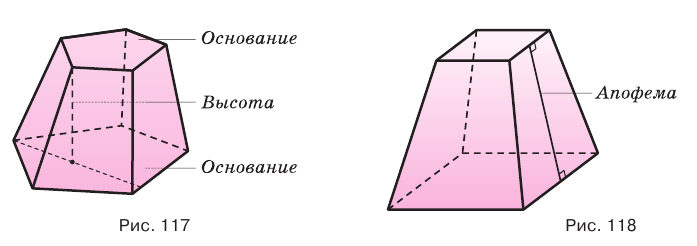
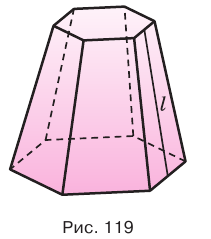
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
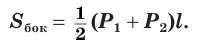
Доказательство:
Пусть есть правильная 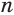 -угольная усеченная пирамида (рис. 119). Пусть
-угольная усеченная пирамида (рис. 119). Пусть 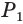 и
и 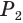 — соответственно периметры нижнего и верхнего оснований и
— соответственно периметры нижнего и верхнего оснований и 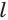 — апофема пирамиды.
— апофема пирамиды.
Боковая поверхность данной пирамиды состоит из 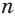 равных трапеций. Пусть
равных трапеций. Пусть 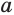 и
и 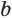 — основания одной из этих трапеций, тогда ее площадь равна
— основания одной из этих трапеций, тогда ее площадь равна 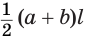 . Учитывая, что боковая поверхность пирамиды состоит из
. Учитывая, что боковая поверхность пирамиды состоит из 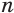 таких трапеций, получим, что
таких трапеций, получим, что
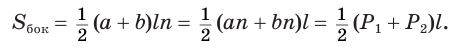
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
Доказательство:
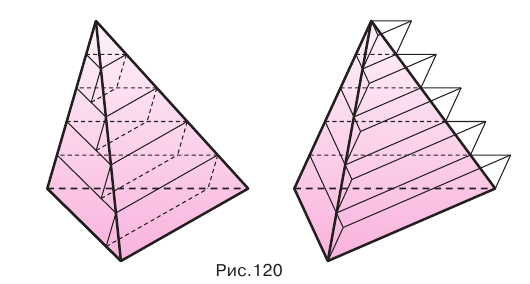
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 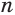 долей и через точки деления проведем плоскости, параллельные основаниям. Этим самым пирамиды разделяются на
долей и через точки деления проведем плоскости, параллельные основаниям. Этим самым пирамиды разделяются на 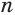 частей. Для каждой части первой пирамиды построим наибольшие по объему призмы, целиком содержащиеся в пирамиде, а для каждой части другой пирамиды — наименьшие по объему призмы, целиком содержащие эту часть.
частей. Для каждой части первой пирамиды построим наибольшие по объему призмы, целиком содержащиеся в пирамиде, а для каждой части другой пирамиды — наименьшие по объему призмы, целиком содержащие эту часть.
Пусть 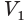 и
и 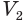 — объемы первой и второй пирамид, a
— объемы первой и второй пирамид, a  и
и  — суммарные объемы призм, построенных для этих пирамид. При счете от оснований пирамид призма в
— суммарные объемы призм, построенных для этих пирамид. При счете от оснований пирамид призма в 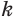 -й части первой пирамиды равновелика призме для
-й части первой пирамиды равновелика призме для 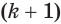 -й части второй пирамиды, так как у этих призм равновелики основания и равные высоты. Поэтому объем
-й части второй пирамиды, так как у этих призм равновелики основания и равные высоты. Поэтому объем  больше объема
больше объема  на объем первой призмы, у которой основанием является основание второй пирамиды, а высота равна
на объем первой призмы, у которой основанием является основание второй пирамиды, а высота равна 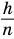 , где
, где 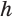 — высота пирамиды (см. рис. 120), т.е.
— высота пирамиды (см. рис. 120), т.е. 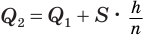 , или
, или 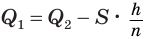 , где
, где 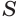 — площадь основания пирамиды. Теперь учтем, что
— площадь основания пирамиды. Теперь учтем, что 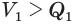 , a
, a 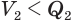 . Поэтому
. Поэтому 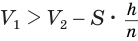 , или
, или 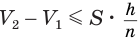 . При увеличении значения переменной
. При увеличении значения переменной 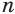 значение выражения
значение выражения 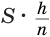 стремится к нулю, а это означает, что
стремится к нулю, а это означает, что 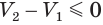 , или
, или

Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство

Из неравенств (1) и (2) следует, что 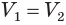 .
.
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
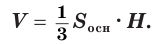
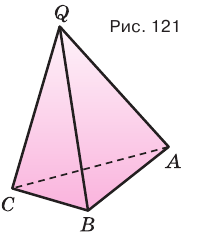
Доказательство:
Пусть есть треугольная пирамида  (рис. 121). Достроим ее до призмы
(рис. 121). Достроим ее до призмы  с основанием
с основанием 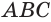 (рис. 122). Отделим от призмы данную пирамиду, получится четырехугольная пирамида
(рис. 122). Отделим от призмы данную пирамиду, получится четырехугольная пирамида 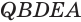 (рис. 122 и 123). Диагональная плоскость
(рис. 122 и 123). Диагональная плоскость 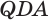 разделяет ее на две пирамиды
разделяет ее на две пирамиды  и
и  , у которых одна и та же высота, проведенная из вершины
, у которых одна и та же высота, проведенная из вершины 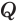 , и равные основания
, и равные основания 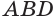 и
и 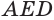 . Поэтому, в соответствии с теоремой 3, пирамиды
. Поэтому, в соответствии с теоремой 3, пирамиды  и
и  равновелики. Сравним пирамиду
равновелики. Сравним пирамиду  с данной пирамидой
с данной пирамидой  . У них равные основания
. У них равные основания 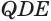 и
и  и высоты, проведенные из вершин
и высоты, проведенные из вершин 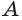 и
и 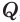 , поэтому эти пирамиды также равновелики. Получается, что все три пирамиды
, поэтому эти пирамиды также равновелики. Получается, что все три пирамиды  ,
,  и
и  равновелики. Поскольку объем призмы
равновелики. Поскольку объем призмы  равен произведению
равен произведению  площади
площади 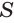 основания
основания  и высоты призмы
и высоты призмы 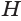 , которая равна высоте пирамиды
, которая равна высоте пирамиды  , то объем пирамиды
, то объем пирамиды  , т. е. третьей части призмы
, т. е. третьей части призмы  , равен третьей доле этого объема, т. е.
, равен третьей доле этого объема, т. е. 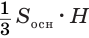 .
.
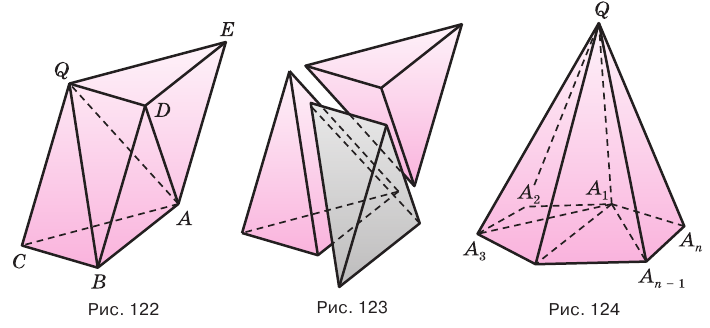
Пусть теперь есть произвольная пирамида 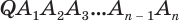 (рис. 124). Через диагонали
(рис. 124). Через диагонали 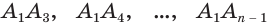 основания
основания 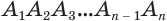 , выходящие из одной вершины
, выходящие из одной вершины 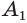 , проведем диагональные сечения, они разделят данную пирамиду на треугольные пирамиды
, проведем диагональные сечения, они разделят данную пирамиду на треугольные пирамиды 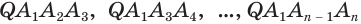 . Поскольку все они имеют общую высоту
. Поскольку все они имеют общую высоту  , то
, то
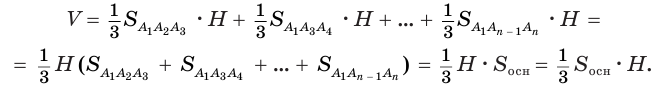
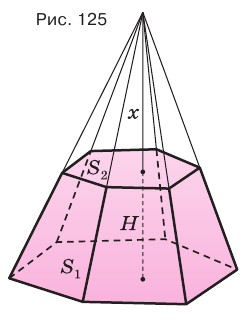
Пример:
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площади 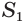 и
и 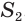 , а высота равна
, а высота равна  (рис. 125).
(рис. 125).
Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна 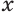 . Искомый объем
. Искомый объем 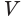 можно найти как разность объемов полной и дополнительной пирамид:
можно найти как разность объемов полной и дополнительной пирамид:
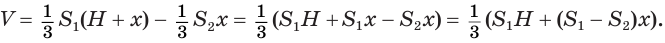
Чтобы найти высоту 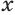 , используем установленное в теореме 1 утверждение о том, что площади сечений пирамиды относятся как квадраты их расстояний от вершины:
, используем установленное в теореме 1 утверждение о том, что площади сечений пирамиды относятся как квадраты их расстояний от вершины:
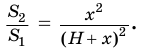
Решим это уравнение, учитывая, что  и
и  — положительные числа:
— положительные числа:
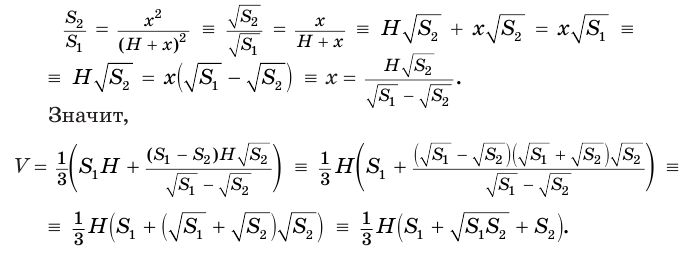
Таким образом, объем 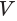 усеченной пирамиды равен третьей доле произведения высоты
усеченной пирамиды равен третьей доле произведения высоты 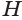 пирамиды и суммы площадей
пирамиды и суммы площадей  и
и  оснований пирамиды и их среднего геометрического
оснований пирамиды и их среднего геометрического 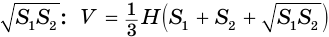 .
.
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Возникновение геометрии
- Призма в геометрии
- Цилиндр в геометрии
- Стереометрия – формулы, определение и вычисление
