Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
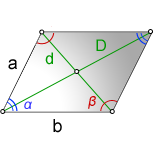
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α, β – углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
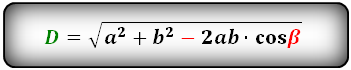
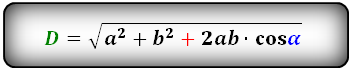
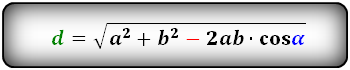

Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
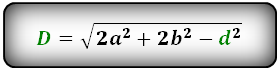
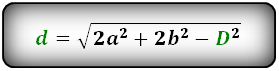
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.

D – большая диагональ
d – меньшая диагональ
α, β – углы между диагоналями
S – площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
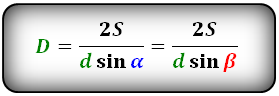
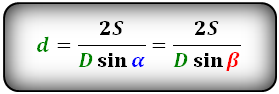
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 03 ноября 2011
-
Обновлено: 13 августа 2021
Параллелограмм представляет собой геометрическую фигуру, где лежащие напротив друг друга ребра
взаимно параллельны.
В задачах по геометрии иногда нужно найти длину его диагонали. В некоторых из них это прямой вопрос,
а в некоторых диагональ нужно вычислить, чтобы потом через нее вычислять другие геометрические
объекты. Например, используя значения длины отрезков, соединяющих вершины, ребер этой геометрической
фигуры, ее углов, вычисляется значение ее площади, другая диагональ. Если в параллелограмме
неизвестны его углы, но известны стороны и угол между диагоналями, то из этих значений узнаются
через расчет углы параллелограмма.
- Длинная диагональ параллелограмма через две стороны и тупой
угол - Короткая диагональ параллелограмма через две стороны и
тупой угол - Длинная диагональ параллелограмма через две стороны и
острый угол - Короткая диагональ параллелограмма через две стороны и
острый угол - Диагональ параллелограмма через две стороны и другую
известную диагональ - Диагональ параллелограмма через площадь, другую известную
диагональ и угол между диагоналями
Длинная диагональ через две стороны и тупой угол
В параллелограмме для вычисления длины наибольшей диагонали при имеющихся данных о его ребрах и тупом
угле между ними следует рассчитать квадрат ребер, суммировать эти значения. После этого умножить
значение одного ребра на другое, на косинус тупого угла между ними, на два. Затем от первой суммы
отнять это произведение и найти из этой разности квадратный корень.
D = √(a² + b² – 2 * a * b * cosβ
где D – диагональ этой геометрической фигуры, a, b – ее ребра, cos β – косинус тупого угла между
ребрами этой фигуры
Цифр после
запятой:
Результат в:
Пример. Значения ребер этого четырехугольника 2 и 4, а косинус тупого угла (120
градусов) между ними -0,5. Диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * (-0,5)) = √(4+16 – 16 *( -0,5)) = √(20 + 8) = 5,3
(ответ округлен)
Диагональ через две стороны и другую известную диагональ
В параллелограмме для вычисления длины проведенной в нем диагонали через его стороны и другую
диагональ следует возвести в квадрат каждую его сторону и умножить на 2 оба результата, затем
сложить полученные значения (это первый результат). Потом следует возвести в квадрат значение длины
другой диагонали (это второй результат). Затем из первого результата вычесть второй и найти из
полученного значения квадратный корень.
D = √(2 * a² + 2 * b² – d²)
где D – диагональ параллелограмма, a, b – его стороны, d – другая диагональ параллелограмма
Цифр после
запятой:
Результат в:
Пример. Пусть стороны параллелограмма 2 и 4, а одна из диагоналей 4. Тогда вторая
диагональ равна: D = √(2 * 2²+ 2 * 4² – 4²) = √(8 + 32 – 16) = √24 = 4,9 (ответ
округленный)
Короткая диагональ через две стороны и тупой угол
Для нахождения наименьшего отрезка соединяющего противоположные вершины в этой геометрической фигуре
через его ребра и тупой угол между ними возводятся в квадрат длины его ребер, складываются
полученные числа (один результат). Далее перемножаются значения длины ребер, косинус тупого угла,
удваивается полученное число (это другой результат). К одному результату прибавляется другой и
находится из полученного значения квадратный корень.
D = √(a² + b² + 2 * a * b * cosβ)
где D – диагональ параллелограмма, a, b – его стороны, cos β – косинус тупого угла между ребрами.
Цифр после
запятой:
Результат в:
Пример. Если ребра этой геометрической фигуры 1 и 3, а косинус тупого угла (120)
между ними -0,5. Тогда диагональ равна: D = √(1²+ 3² + 2 * 1 * 3 * (-0,5)) = √(1 + 9 + 6 * (-0,5)) = √(10 – 3) = 2,6
(ответ округлен)
Длинная диагональ через две стороны и острый угол
В этом четырехугольнике для расчета значения протяженности большего отрезка, соединяющего в нем
расположенные друг напротив друга вершины, через два его ребра и острый угол нужно сначала возвести
в квадрат значение длины его ребер, потом складываются результаты этого вычисления (это первое
слагаемое для последующего сложения). Затем умножаются длины ребер друг на друга, на косинус острого
угла, найденное произведение еще на 2 (это второе слагаемое). Затем оба слагаемых складываются и из
суммы вычисляется квадратный корень.
D = √(a² + b² + 2 * a * b * cos α)
где D – диагональ этой геометрической фигуры, a, b – его ребра, cos α – косинус острого угла
Цифр после
запятой:
Результат в:
Пример. Если ребра этого четырехугольника 2 и 5, а косинус острого угла (60
градусов) 0,5. Тогда диагональ рассчитывается: D = √(2²+ 5² + 2 * 2 * 5 * 0,5) = √(4 + 25 + 20 * 0,5 = √(29 + 10) = 6,2
(округленно)
Короткая диагональ через две стороны и острый угол
В параллелограмме для вычисления длины наименьшей проведенной в нем диагонали через его стороны и
острый угол между ними следует возвести в квадрат каждую его сторону, затем сложить полученные
значения (это первый результат). Потом следует перемножить между собой стороны, косинус тупого угла
между ними, удвоить полученное значение (это второй результат). Затем из первого результата вычесть
второй и найти из полученного значения квадратный корень.
D = √(a² + b²– 2 * a * b * cosα)
где D – диагональ параллелограмма, a, b – его стороны, cos α – косинус острого угла между сторонами
параллелограмма
Цифр после
запятой:
Результат в:
Пример. Пусть стороны параллелограмма 2 и 4, а косинус острого угла (60) между ними
0,5. Тогда диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * 0,5) = √(4 + 16 – 16 * 0,5) = √(20 — 8) = 3,5
(ответ округлен)
Диагональ через площадь, другую известную диагональ и угол между диагоналями
В параллелограмме для вычисления длины проведенного в нем отрезка, соединяющего противоположные
вершины, используя значение его площади, другой диагонали и угол между диагоналями, следует удвоить
значение его площади (это первый результат). Потом следует умножить значение длины другого отрезка,
соединяющего противоположные вершины, на синус угла между диагоналями (это второй результат). Затем
следует разделить первый результат на второй.
D = (2 * S) / (d * sin α)
где D – диагональ параллелограмма, S – площадь параллелограмма, d – вторая диагональ этой
геометрической фигуры, sinα – синус угла между диагоналями параллелограмма
Цифр после
запятой:
Результат в:
Пример. Значение площади составляет 30, одна из диагоналей 4, синус угла (30
градусов) между диагоналями 0,5. Тогда другая диагональ равна: D = 2 * 30 / 4 * 0,5 = 60 / 2 = 30

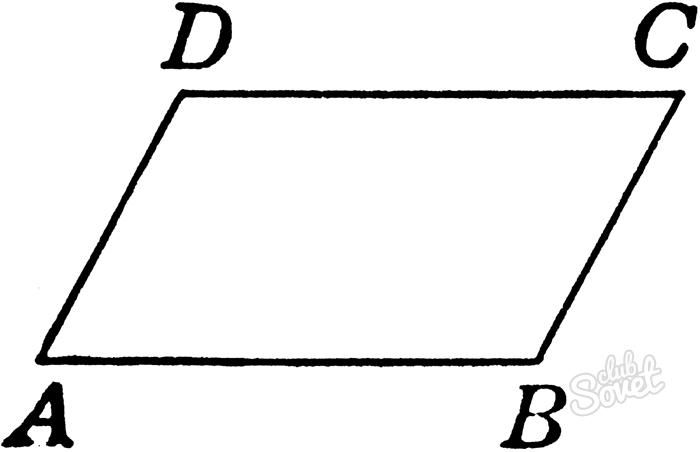
Как найти диагональ параллелограмма
Четырехугольник, противоположные стороны которого параллельны, является параллелограммом. Диагонали – это прямые, соединяющие противоположные вершины. Точка их пересечения является центром симметрии. В общем случае у параллелограмма есть две диагонали, D – длинная и d – короткая.
1
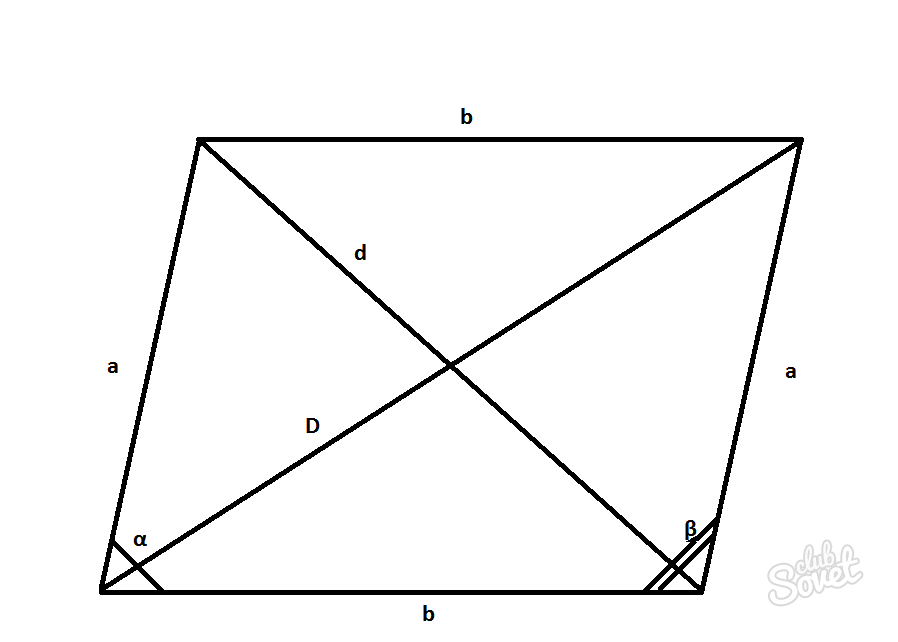
Найти диагональ параллелограмма по теореме косинусов
Для применения этого метода необходимо знать:
- Длины сторон параллелограмма a и b.
- Значение косинусов углов параллелограмма α и β.
D = √a^2 + b^2 – 2ab·cosβ
d = √a^2 + b^2 + 2ab·cosβ
D = √a^2 + b^2 + 2ab·cosα
d = √a^2 + b^2 – 2ab·cosα
2
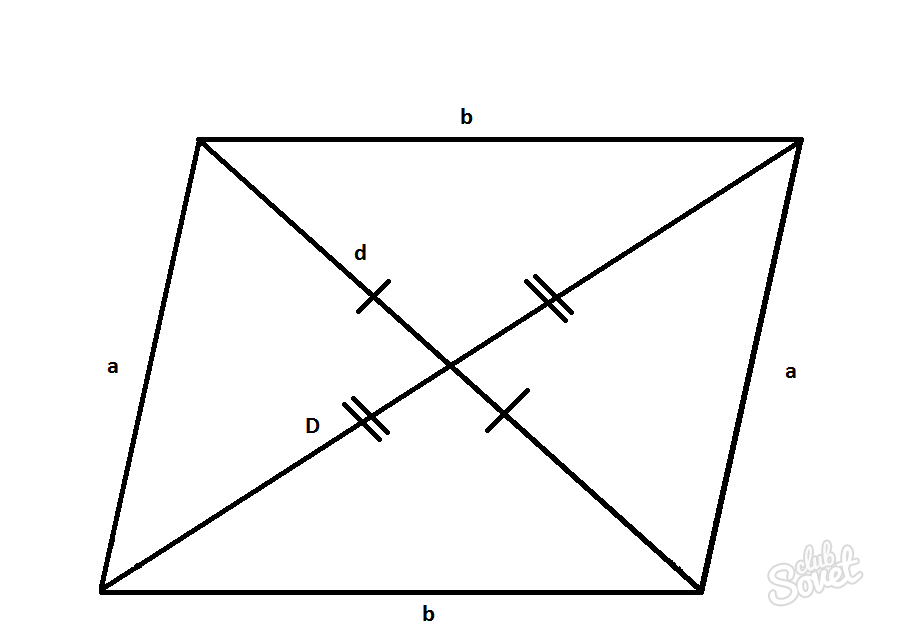
Найти диагональ параллелограмма через одну известную диагональ и стороны
Для применения этого метода необходимо знать:
- Длины сторон параллелограмма a и b.
- Длину одной из диагоналей D или d.
D = √2a^2 + 2b^2 – d^2
d = √2a^2 + 2b^2 – D^2
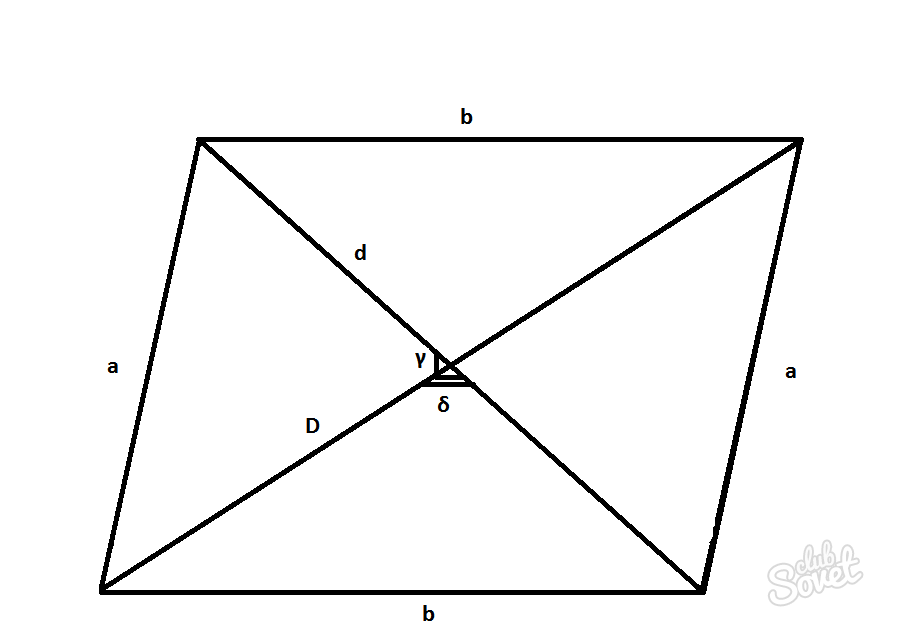
Найти диагональ параллелограмма через площадь, одну известную диагональ и угол между диагоналями
Для применения этого метода необходимо знать:
- Площадь параллелограмма.
- Длину одной из диагоналей D или d.
- Угол между диагоналями γ или δ.
D = 2S/d·sinγ = 2S/d·sinδ
d = 2S/D·sinγ = 2S/D·sinδ
4
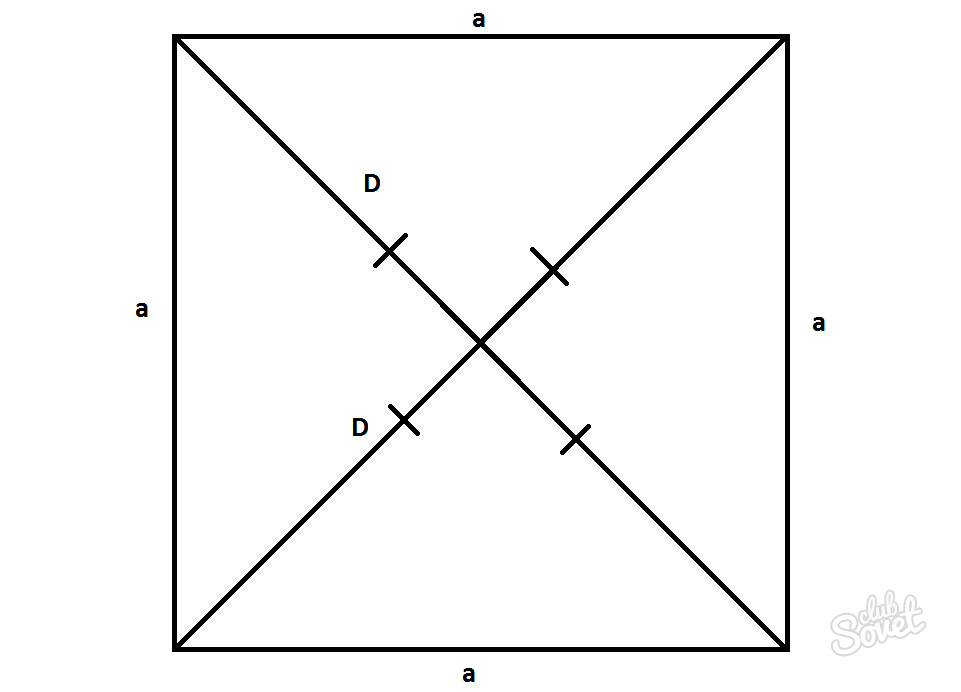
Частный случай определения длины диагонали параллелограмма – квадрат
Квадрат – это параллелограмм, в котором все стороны равны и углы составляют 90°. Длины диагоналей в таком случае будут равны D=d и могут быть рассчитаны по теореме Пифагора.
D=d=a*√2
5
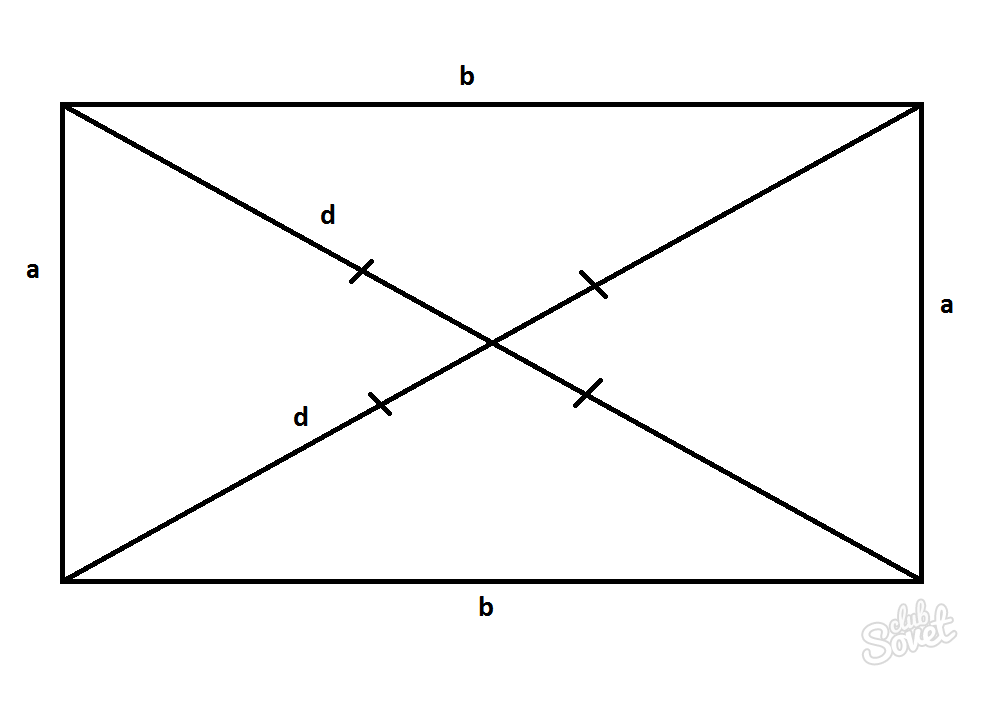
Частный случай определения длины диагонали параллелограмма – прямоугольник
Прямоугольник – это параллелограмм, в котором углы равны и составляют 90°. Длины диагоналей в таком случае будут равны D=d и могут быть рассчитаны по теореме Пифагора.
D=d=√(а^2+b^2)
Геометрический калькулятор для прямоугольного параллелепипеда можно запустить также, зная два из трех ребер тела и его диагональ. Поскольку диагональ параллелепипеда равна по теореме Пифагора квадратному корню из суммы квадратов всех трех его ребер, то из этого выражения алгебраически можно вывести формулу для третьего неизвестного ребра. (рис.22.4)
d_4=√(a^2+b^2+c^2 )
b=√(a^2+c^2-〖d_4〗^2 )
Имея возможность вычислить неизвестное ребро параллелепипеда, можно следом найти все остальные диагонали его боковых граней. (рис.22.1, 22.2, 22.3)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )=√(a^2+a^2+c^2-〖d_4〗^2 )=√(2a^2+c^2-〖d_4〗^2 )
d_3=√(b^2+c^2 )=√(a^2+c^2-〖d_4〗^2+c^2 )=√(a^2+2c^2-〖d_4〗^2 )
Чтобы найти угол α между диагональю прямоугольного параллелепипеда и диагональю его основания, необходимо воспользоваться отношением синуса – известного бокового ребра а к диагонали параллелепипеда. (рис.22.5)
sinα=a/d_4
Периметр прямоугольного параллелепипеда равен учетверенной сумме ребер, составляющих параллелепипед. Для неизвестного ребра в формулу подставляется полученное из теоремы Пифагора выражение через диагональ параллелепипеда.
P=4(a+b+c)
Площадь полной поверхности прямоугольного параллелепипеда через диагональ также можно вычислить посредством замены неизвестной переменной на соответствующее выражение. Изначально площадь параллелепипеда равна удвоенной сумме попарных произведений его ребер.
S=2(ab+bc+ac)=2((a+c) √(a^2+c^2-〖d_4〗^2 )+ac)
Чтобы найти объем прямоугольного параллелепипеда, зная диагональ, нужно умножить два известных ребра параллелепипеда на квадратный корень из разности квадрата диагонали от суммы квадратов этих ребер.
V=abc=ac√(a^2+c^2-〖d_4〗^2 )
- Диагональ прямоугольника
- Диагональ квадрата
- Диагональ куба
- Диагональ прямоугольного параллелепипеда
- Диагонали ромба
- Диагонали параллелограмма
- Диагонали трапеции
Добавить в закладки
Диагонали параллелограмма
Сторона a
Сторона b
Угол в градусах α
Знаков после запятой
Поделиться в социальных сетях:
или https://correctcalc.ru/formula-diagonali/diagonali-parallelogramma/ скопировать ссылку на страницу
Параллель — четырехугольник, в котором по определению параллельные стороны параллельные и равные. Таким образом, и противоположные параллельные углы будут равны между собой, и поскольку все углы четырехугольника равны 360 градусов, можно вывести, что и две последовательные углы будут равны 180 градусов. Это свойство играет значительную роль в том, чтобы найти параллельные диагонали, учитывая разную длину.
0 Комментариев |
; ; ; ; ;
Войти
Наш сайт использует файлы cookie, чтобы улучшить работу сайта, повысить его эффективность и удобство. Продолжая использовать сайт correctcalc.ru, вы соглашаетесь на использование файлов cookie.
