Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
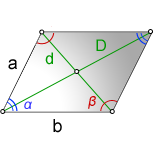
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α, β – углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
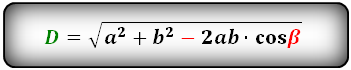
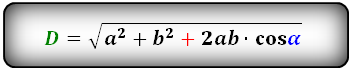
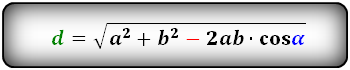

Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
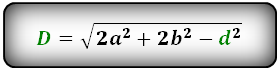
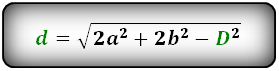
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.

D – большая диагональ
d – меньшая диагональ
α, β – углы между диагоналями
S – площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
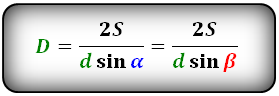
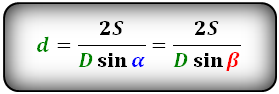
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 03 ноября 2011
-
Обновлено: 13 августа 2021
Параллелограмм представляет собой геометрическую фигуру, где лежащие напротив друг друга ребра
взаимно параллельны.
В задачах по геометрии иногда нужно найти длину его диагонали. В некоторых из них это прямой вопрос,
а в некоторых диагональ нужно вычислить, чтобы потом через нее вычислять другие геометрические
объекты. Например, используя значения длины отрезков, соединяющих вершины, ребер этой геометрической
фигуры, ее углов, вычисляется значение ее площади, другая диагональ. Если в параллелограмме
неизвестны его углы, но известны стороны и угол между диагоналями, то из этих значений узнаются
через расчет углы параллелограмма.
- Длинная диагональ параллелограмма через две стороны и тупой
угол - Короткая диагональ параллелограмма через две стороны и
тупой угол - Длинная диагональ параллелограмма через две стороны и
острый угол - Короткая диагональ параллелограмма через две стороны и
острый угол - Диагональ параллелограмма через две стороны и другую
известную диагональ - Диагональ параллелограмма через площадь, другую известную
диагональ и угол между диагоналями
Длинная диагональ через две стороны и тупой угол
В параллелограмме для вычисления длины наибольшей диагонали при имеющихся данных о его ребрах и тупом
угле между ними следует рассчитать квадрат ребер, суммировать эти значения. После этого умножить
значение одного ребра на другое, на косинус тупого угла между ними, на два. Затем от первой суммы
отнять это произведение и найти из этой разности квадратный корень.
D = √(a² + b² – 2 * a * b * cosβ
где D – диагональ этой геометрической фигуры, a, b – ее ребра, cos β – косинус тупого угла между
ребрами этой фигуры
Цифр после
запятой:
Результат в:
Пример. Значения ребер этого четырехугольника 2 и 4, а косинус тупого угла (120
градусов) между ними -0,5. Диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * (-0,5)) = √(4+16 – 16 *( -0,5)) = √(20 + 8) = 5,3
(ответ округлен)
Диагональ через две стороны и другую известную диагональ
В параллелограмме для вычисления длины проведенной в нем диагонали через его стороны и другую
диагональ следует возвести в квадрат каждую его сторону и умножить на 2 оба результата, затем
сложить полученные значения (это первый результат). Потом следует возвести в квадрат значение длины
другой диагонали (это второй результат). Затем из первого результата вычесть второй и найти из
полученного значения квадратный корень.
D = √(2 * a² + 2 * b² – d²)
где D – диагональ параллелограмма, a, b – его стороны, d – другая диагональ параллелограмма
Цифр после
запятой:
Результат в:
Пример. Пусть стороны параллелограмма 2 и 4, а одна из диагоналей 4. Тогда вторая
диагональ равна: D = √(2 * 2²+ 2 * 4² – 4²) = √(8 + 32 – 16) = √24 = 4,9 (ответ
округленный)
Короткая диагональ через две стороны и тупой угол
Для нахождения наименьшего отрезка соединяющего противоположные вершины в этой геометрической фигуре
через его ребра и тупой угол между ними возводятся в квадрат длины его ребер, складываются
полученные числа (один результат). Далее перемножаются значения длины ребер, косинус тупого угла,
удваивается полученное число (это другой результат). К одному результату прибавляется другой и
находится из полученного значения квадратный корень.
D = √(a² + b² + 2 * a * b * cosβ)
где D – диагональ параллелограмма, a, b – его стороны, cos β – косинус тупого угла между ребрами.
Цифр после
запятой:
Результат в:
Пример. Если ребра этой геометрической фигуры 1 и 3, а косинус тупого угла (120)
между ними -0,5. Тогда диагональ равна: D = √(1²+ 3² + 2 * 1 * 3 * (-0,5)) = √(1 + 9 + 6 * (-0,5)) = √(10 – 3) = 2,6
(ответ округлен)
Длинная диагональ через две стороны и острый угол
В этом четырехугольнике для расчета значения протяженности большего отрезка, соединяющего в нем
расположенные друг напротив друга вершины, через два его ребра и острый угол нужно сначала возвести
в квадрат значение длины его ребер, потом складываются результаты этого вычисления (это первое
слагаемое для последующего сложения). Затем умножаются длины ребер друг на друга, на косинус острого
угла, найденное произведение еще на 2 (это второе слагаемое). Затем оба слагаемых складываются и из
суммы вычисляется квадратный корень.
D = √(a² + b² + 2 * a * b * cos α)
где D – диагональ этой геометрической фигуры, a, b – его ребра, cos α – косинус острого угла
Цифр после
запятой:
Результат в:
Пример. Если ребра этого четырехугольника 2 и 5, а косинус острого угла (60
градусов) 0,5. Тогда диагональ рассчитывается: D = √(2²+ 5² + 2 * 2 * 5 * 0,5) = √(4 + 25 + 20 * 0,5 = √(29 + 10) = 6,2
(округленно)
Короткая диагональ через две стороны и острый угол
В параллелограмме для вычисления длины наименьшей проведенной в нем диагонали через его стороны и
острый угол между ними следует возвести в квадрат каждую его сторону, затем сложить полученные
значения (это первый результат). Потом следует перемножить между собой стороны, косинус тупого угла
между ними, удвоить полученное значение (это второй результат). Затем из первого результата вычесть
второй и найти из полученного значения квадратный корень.
D = √(a² + b²– 2 * a * b * cosα)
где D – диагональ параллелограмма, a, b – его стороны, cos α – косинус острого угла между сторонами
параллелограмма
Цифр после
запятой:
Результат в:
Пример. Пусть стороны параллелограмма 2 и 4, а косинус острого угла (60) между ними
0,5. Тогда диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * 0,5) = √(4 + 16 – 16 * 0,5) = √(20 — 8) = 3,5
(ответ округлен)
Диагональ через площадь, другую известную диагональ и угол между диагоналями
В параллелограмме для вычисления длины проведенного в нем отрезка, соединяющего противоположные
вершины, используя значение его площади, другой диагонали и угол между диагоналями, следует удвоить
значение его площади (это первый результат). Потом следует умножить значение длины другого отрезка,
соединяющего противоположные вершины, на синус угла между диагоналями (это второй результат). Затем
следует разделить первый результат на второй.
D = (2 * S) / (d * sin α)
где D – диагональ параллелограмма, S – площадь параллелограмма, d – вторая диагональ этой
геометрической фигуры, sinα – синус угла между диагоналями параллелограмма
Цифр после
запятой:
Результат в:
Пример. Значение площади составляет 30, одна из диагоналей 4, синус угла (30
градусов) между диагоналями 0,5. Тогда другая диагональ равна: D = 2 * 30 / 4 * 0,5 = 60 / 2 = 30
Параллелограмм – это четырехугольник, у которого по определению противоположные стороны параллельны и равны. Как следствие, противоположные углы параллелограмма также будут между собой равны, а так как сумма всех углов в четырехугольнике равна 360 градусам, то можно сделать вывод, что сумма двух последовательных углов будет равна 180 градусам. Данное свойство будет играть существенную роль для нахождения диагоналей параллелограмма, с учетом того, что они разной длины.
Так как каждая диагональ параллелограмма делит его на два равновеликих треугольника, именно их свойства и будут использованы для выведения формулы диагонали параллелограмма.
В любом треугольнике угол и сторона, лежащие напротив, пропорциональны друг другу. Для параллелограмма это будет значить, что более длинная диагональ будет лежать напротив тупого угла, а более короткая диагональ – напротив острого.С учетом того, что стороны треугольников, полученных в результате проведения диагоналей, одинаковы – это стороны параллелограмма, значение градусной меры угла между данными сторонами определяет чему будет равна длина диагонали,вычисленной по формуле. Другими словами, если в формулудиагонали подставить значение острого угла параллелограмма, то калькулятор вычислит длину короткой диагонали, а если подставить значение тупого угла – то длинной.
Для того чтобы перейти от одного угла к другому, используется разность 180 градусов и заданного угла, таким образом калькулятор одновременно может вычислить обе диагонали.
α=180°-β
Чтобы вывести формулу диагонали параллелограмма, используется теорема косинусов в треугольнике, который диагональ образует со сторонами. В любом из подобных треугольников, диагональ является стороной, противолежащей углу параллелограмма и, соответственно, ее квадрат равен сумме квадратов двух других сторон треугольника (сторон параллелограмма, в данном случае) за вычетом удвоенного произведения тех же сторон на косинус приведенного угла. Чтобы найти длину диагонали параллелограмма, калькулятор вычисляет квадратный корень из данного выражения.
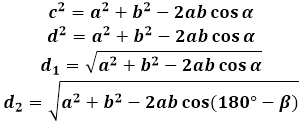
A parallelogram is defined as a quadrilateral that has equal pairs of opposite sides and angles. One of its pairs of opposite sides is parallel to each other. The interior angles lying on the supplementary in nature, that is, their sum is 180 degrees. The diagonals of a parallelogram bisect each other, that is, they divide each other in two equal parts. The sum of all interior angles of a parallelogram is 360 degrees.

The above figure depicts a parallelogram ABCD with sides AB, BC, CD and AD and diagonals AC and BD. Here the lengths of opposite sides AB and CD are equal to each other. Similarly, the lengths of BC and AD are the same. The pairs of opposite angles, that is, ∠A and ∠C and ∠B and ∠D are equal to each other.
Diagonal of Parallelogram Formula
The formula for the length of a diagonal of a parallelogram is equal to the magnitude of the resultant of any two adjacent sides.
x = √(a2 + b2 – 2ab cos A) = √(a2 + b2 + 2ab cos B)
y = √(a2 + b2 + 2ab cos A) = √(a2 + b2 – 2ab cos B)
where,
x and y are the lengths of diagonals,
a and b are adjacent side lengths,
A and B are the angles formed between the sides.
The diagonal lengths and sides of a parallelogram have a relation between each other. The sum of squares of diagonals is equal to twice the sum of squares of two adjacent sides.
x2 + y2 = 2(a2 + b2)
where,
x and y are diagonal lengths,
a and b are adjacent side lengths.
Sample Problems
Problem 1. Calculate the length of the diagonals of a parallelogram of side lengths 5 m and 10 m, if one of the interior angles is 60°.
Solution:
We have,
a = 5
b = 10
∠A = 60°
∠B = 120°
We have to find the diagonal lengths x and y.
Using the formula we get,
x = √(a2 + b2 – 2ab cos A)
= √(52 + 102 – 2 (5) (10) cos 60°)
= √75
= 8.66 m
y = √(a2 + b2 + 2ab cos A)
= √(52 + 102 + 2 (5) (10) cos 60°)
= √175
= 13.22 m
Problem 2. Calculate the length of the diagonals of a parallelogram of side lengths 4 m and 7 m, if one of the interior angles is 30°.
Solution:
We have,
a = 4
b = 7
∠A = 30°
We have to find the diagonal lengths x and y.
Using the formula we get,
x = √(a2 + b2 – 2ab cos A)
= √(42 + 72 – 2 (4) (7) cos 30°)
= √16.48
= 4.06 m
y = √(a2 + b2 + 2ab cos A)
= √(42 + 72 + 2 (4) (7) cos 30°)
= √73.63
= 8.5 m
Problem 3. Calculate the length of one of the diagonals of a parallelogram of side lengths 5 m and 9 m, if one of the interior angles is 25°.
Solution:
We have,
a = 5
b = 9
∠A = 25°
We have to find the diagonal length.
Using the formula we get,
x = √(a2 + b2 – 2ab cos A)
= √(52 + 92 – 2 (5) (9) cos 25°)
= √24.40
= 4.06 m
Problem 4. Calculate the length of one of the diagonals of a parallelogram of side lengths 12 m and 16 m, if one of the interior angles is 37°.
Solution:
We have,
a = 12
b = 16
∠A = 37°
We have to find the diagonal length.
Using the formula we get,
x = √(a2 + b2 – 2ab cos A)
= √(122 + 162 – 2 (12) (16) cos 37°)
= √93.315
= 9.66 m
Problem 5. Calculate the length of one of the diagonals of a parallelogram of side lengths 4 m and 6 m, if the other diagonal is 8 m.
Solution:
We have,
a = 4
b = 6
x = 8
Using the formula we get,
x2 + y2 = 2(a2 + b2)
=> 82 + y2 = 2 (42 + 62)
=> 64 + y2 = 2 (16 + 36)
=> 64 + y2 = 104
=> y2 = 40
=> y = 6.32 m
Problem 6. Calculate the length of one of the diagonals of a parallelogram of side lengths 8 m and 12 m, if the other diagonal is 14 m.
Solution:
We have,
a = 8
b = 12
x = 14
Using the formula we get,
x2 + y2 = 2(a2 + b2)
=> 142 + y2 = 2 (82 + 122)
=> 196 + y2 = 2 (16 + 144)
=> 196 + y2 = 320
=> y2 = 124
=> y = 11.13 m
Problem 7. Calculate the length of one of the diagonals of a parallelogram of side lengths 7 m and 9 m, if the other diagonal is 11 m.
Solution:
We have,
a = 7
b = 9
x = 11
Using the formula we get,
x2 + y2 = 2(a2 + b2)
=> 112 + y2 = 2 (72 + 92)
=> 121 + y2 = 2 (49 + 81)
=> 121 + y2 = 260
=> y2 = 139
=> y = 11.78 m
Last Updated :
30 Apr, 2022
Like Article
Save Article
Содержание
- – Как искать диагональ в параллелограмме?
- – Как найти 2 диагональ в параллелограмме?
- – Где пересекаются диагонали параллелограмма?
- – Как провести высоту параллелограмма?
- – Как найти боковые стороны параллелограмма?
- – Как найти диагональ в параллелограмме через стороны?
- – Как найти длину диагонали параллелепипеда?
- – Как найти диагональ в трапеции?
- – Как найти большую высоту параллелограмма?
- – Что известно про диагонали параллелограмма?
- – В каком параллелепипеде все диагонали равны?
- – Как доказать что диагонали параллелограмма равны?
- – Что такое большая высота в параллелограмме?
- – Как найти высоту в прямоугольном треугольнике?
- – Как найти S параллелограмма?
Как искать диагональ в параллелограмме?
Как найти диагонали параллелограмма
- Диагональ параллелограмма можно найти через длины его сторон и косинус угла между ними (Формулы 1-4)
- Также диагональ может быть найдена через длины сторон и размер второй диагонали (Формулы 5-6)
Как найти 2 диагональ в параллелограмме?
В параллелограмме точка пересечения диагоналей делит их пополам. Любая диагональ параллелограмма делит его на два равных треугольника. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Где пересекаются диагонали параллелограмма?
Точка пересечения диагоналей является центром симметрии параллелограмма. Параллелограмм диагональю делится на два равных треугольника. Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
Как провести высоту параллелограмма?
В параллелограмме могут быть проведены две высоты. Одна из них опускается из верхнего угла на противоположную, длинную сторону, разделяя параллелограмм на прямоугольный треугольник и прямоугольную трапецию. Вторая высота опускается на короткую сторону параллелограмма.
Как найти боковые стороны параллелограмма?
Зная диагонали параллелограмма и одну его сторону, можно найти вторую сторону. Для этого нужно извлечь квадратный корень из половины суммы квадратов диагоналей без удвоенного квадрата известной стороны.
Как найти диагональ в параллелограмме через стороны?
В любом из подобных треугольников, диагональ является стороной, противолежащей углу параллелограмма и, соответственно, ее квадрат равен сумме квадратов двух других сторон треугольника (сторон параллелограмма, в данном случае) за вычетом удвоенного произведения тех же сторон на косинус приведенного угла.
Как найти длину диагонали параллелепипеда?
Четыре диагонали параллелепипеда, пересекаясь в одной точке, одновременно делятся пополам. Формула нахождения длины диагонали: квадрат диагонали равен сумме квадратов трех измерений параллелограмма.
Как найти диагональ в трапеции?
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
- Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. …
- Данная формула получена путем преобразования предыдущей формулы.
Как найти большую высоту параллелограмма?
е. высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей стороны и отсекаемой высотой части основания. Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 3 см, то длина высоты будет: h=?(5^2-3^2)=4 (см).
Что известно про диагонали параллелограмма?
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. Диагональю параллелограмма называется отрезок, соединяющий противоположные вершины параллелограмма.
В каком параллелепипеде все диагонали равны?
В прямоугольном параллелепипеде все диагонали равны.
Как доказать что диагонали параллелограмма равны?
Если диагонали параллелограмма равны, то он является прямоугольником.
- AC=BD (по условию).
- Сторона AD — общая.
- AB=CD (как противолежащие стороны параллелограмма).
Что такое большая высота в параллелограмме?
Большая высота высота параллелограмма — это высота, проведенная к ее меньшей стороне. На рисунке 3 BK и BM — высоты параллелограмма ABCD, проведенные из вершины тупого угла B. Из них BM — большая высота параллелограмма ABCD, BK — его меньшая высота.
Как найти высоту в прямоугольном треугольнике?
Примеры решения задач
| Задание | В прямоугольном треугольнике катеты равны см и см. Найти высоту , опущенную на гипотенузу . |
|---|---|
| Решение | Пусть катет см, а см (рис. 2). Тогда по теореме Пифагора гипотенуза см Площадь прямоугольного треугольника равна половине произведения катетов, т.е. Высоту найдем по формуле |
| Ответ | см |
Как найти S параллелограмма?
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне. 2. Площадь параллелограмма равна произведению сторон на синус угла между ними.
Интересные материалы:
Как стереть чернила с бумаги без следов?
Как стереть картинку с чехла?
Как стереть корректор с бумаги?
Как стереть краску с линолеума?
Как стереть краску со штанов?
Как стереть маркер с кожаной обуви?
Как стереть маркер с меловой доски?
Как стереть маркер с пластика?
Как стереть масляную краску?
Как стереть надпись ручкой с бумаги?
