Версия для печати и копирования в MS Word
Найдите длину (в метрах) диагонали поля для мини‐футбола.
На плане (см. рис.) изображена детская площадка, расположенная в общем дворе двух многоквартирных домов (сторона самой маленькой клетки на плане равна 1 м). Площадка предназначена как для детей младшего возраста, так и для школьников, поэтому она разделена на две отдельные части. При этом по краю зоны для малышей есть специальная дорожка, по которой можно кататься на роликах, машинках, велосипедах и просто бегать. Прямо перед скамейкой расположился игровой комплекс с горкой, домиком, лесенками, а слева от скамейки находится песочница, площадь которой равна 16 м2. Карусель отмечена на плане цифрой 6. Кроме того, в зоне для малышей имеются качели. В зоне для школьников находятся: комплекс уличных тренажёров, обозначенный цифрой 1, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. При этом поле для мини‐футбола имеет самую большую площадь, а верёвочный комплекс — самую маленькую.
Спрятать решение
Решение.
Найдём длину диагонали поля для мини‐футбола по теореме Пифагора:
м.
Ответ: 20.
Источник: Тренировочный вариант № 233, Александр Ларин
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Качели | Поле для мини‐ футбола |
Верёвочный комплекс |
Песочница |
|---|---|---|---|---|
| Цифры |
Источник: Тренировочный вариант № 233, Александр Ларин
2
Сколько кубических метров песка понадобилось, чтобы слой песка в песочнице был 20 см?
Источник: Тренировочный вариант № 233, Александр Ларин
3
Найдите площадь (в м2), игрового комплекса для малышей.
Источник: Тренировочный вариант № 233, Александр Ларин
4
Жители домов тщательно изучили современные материалы для мощения детской площадки. Было решено уложить в тех зонах, где есть риск получить травму, современное резиновое бесшовное покрытие. Такими зонами оказались площадка для малышей (за исключением песочницы, но включая дорожку), комплекс уличных тренажёров, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. Цены на материалы и монтаж приведены в таблице.
| Площадь (м2) | менее 100 | 100‐250 | 250‐500 | более 500 |
|---|---|---|---|---|
| Цена (руб./м2) | 1500 | 1470 | 1430 | 1400 |
Заказ на все площадки делается одновременно, и стоимость заказа зависит от суммарной площади. На сколько рублей дороже оказалось покрыть площадку для малышей, чем площадку для школьников?
Источник: Тренировочный вариант № 233, Александр Ларин
Найдите длину (в метрах) диагонали поля для мини‐футбола.
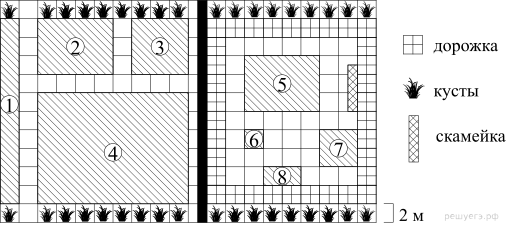
На плане (см. рисунок) изображена детская площадка, расположенная в общем дворе двух многоквартирных домов (сторона самой маленькой клетки на плане равна 1 м). Площадка предназначена как для детей младшего возраста, так и для школьников, поэтому она разделена на две отдельные части. При этом по краю зоны для малышей есть специальная дорожка, по которой можно кататься на роликах, машинках, велосипедах и просто бегать. Прямо перед скамейкой расположился игровой комплекс с горкой, домиком, лесенками, а слева от скамейки находится песочница, площадь которой равна 16 м2. Карусель отмечена на плане цифрой 6. Кроме того, в зоне для малышей имеются качели. В зоне для школьников находятся: комплекс уличных тренажёров, обозначенный цифрой 1, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. При этом поле для мини‐футбола имеет самую большую площадь, а верёвочный комплекс — самую маленькую.
Решение.
Найдём длину диагонали поля для мини‐футбола по теореме Пифагора:
 м.
м.
Ответ: 20.
На плане (см. рисунок) изображена детская площадка, расположенная в общем дворе двух многоквартирных домов (сторона самой маленькой клетки на плане равна 1 м). Площадка предназначена как для детей младшего возраста, так и для школьников, поэтому она разделена на две отдельные части. При этом по краю зоны для малышей есть специальная дорожка, по которой можно кататься на роликах, машинках, велосипедах и просто бегать. Прямо перед скамейкой расположился игровой комплекс с горкой, домиком, лесенками, а слева от скамейки находится песочница, площадь которой равна 16 м2. Карусель отмечена на плане цифрой 6. Кроме того, в зоне для малышей имеются качели. В зоне для школьников находятся: комплекс уличных тренажёров, обозначенный цифрой 1, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. При этом поле для мини‐футбола имеет самую большую площадь, а верёвочный комплекс – самую маленькую.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Качели | Поле для мини‐футбола | Верёвочный комплекс | Песочница |
| Цифры |
2. Сколько кубических метров песка понадобилось, чтобы слой песка в песочнице был 20 см?
3. Найдите площадь (в м2), игрового комплекса для малышей.
4. Найдите длину (в метрах) диагонали поля для мини‐футбола.
Жители домов тщательно изучили современные материалы для мощения детской площадки. Было решено уложить в тех зонах, где есть риск получить травму, современное резиновое бесшовное покрытие. Такими зонами оказались площадка для малышей (за исключением песочницы, но включая дорожку), комплекс уличных тренажёров, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. Цены на материалы и монтаж приведены в таблице.
| Площадь (м2) | менее 100 | 100‐250 | 250‐500 | более 500 |
| Цена (руб./м2) | 1500 | 1470 | 1430 | 1400 |
5. Заказ на все площадки делается одновременно, и стоимость заказа зависит от суммарной площади. На сколько рублей дороже оказалось покрыть площадку для малышей, чем площадку для школьников?
Вариант № 13
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
|
Объекты |
Качели |
Поле для мини‐ |
Верёвочный |
Песочница |
|
Цифры |

На плане (см. рисунок) изображена детская площадка, расположенная в общем дворе двух многоквартирных домов (сторона самой маленькой клетки на плане равна 1 м). Площадка предназначена как для детей младшего возраста, так и для школьников, поэтому она разделена на две отдельные части. При этом по краю зоны для малышей есть специальная дорожка, по которой можно кататься на роликах, машинках, велосипедах и просто бегать. Прямо перед скамейкой расположился игровой комплекс с горкой, домиком, лесенками, а слева от скамейки находится песочница, площадь которой равна 16 м2. Карусель отмечена на плане цифрой 6. Кроме того, в зоне для малышей имеются качели. В зоне для школьников находятся: комплекс уличных тренажёров, обозначенный цифрой 1, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. При этом поле для мини‐футбола имеет самую большую площадь, а верёвочный комплекс — самую маленькую.
Решение. Прямо перед скамейкой расположился игровой комплекс с горкой, домиком, лесенками, а слева от скамейки находится песочница, площадь которой равна 16 м2. Карусель отмечена на плане цифрой 6. Кроме того, в зоне для малышей имеются качели. Значит, качели отмечены цифрой 8, а песочница — цифрой 7. В зоне для школьников находятся: комплекс уличных тренажёров, обозначенный цифрой 1, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. При этом поле для мини‐футбола имеет самую большую площадь, а верёвочный комплекс — самую маленькую. Следовательно, поле для мини-футбола отмечено цифрой 4, а верёвочный комплекс — цифрой 3.
Ответ: 8437.
2. Сколько кубических метров песка понадобилось, чтобы слой песка в песочнице был 20 см?
Решение. Поскольку площадь песочницы равна 16 м2, чтобы слой песка в песочнице был 20 см, то есть ![]() м, понадобилось
м, понадобилось ![]() м3 песка.
м3 песка.
Ответ: 3,2.
3. Найдите площадь (в м2), игрового комплекса для малышей.
Решение. Заметим, что клетка имеет размер 2 х 2 м, размеры игрового комплекса для малышей — 4 x 3 клетки. Значит, площадь игрового комплекса для малышей равна
![]() м2.
м2.
Ответ: 48.
4. Найдите длину (в метрах) диагонали поля для мини‐футбола.
Решение. Найдём длину диагонали поля для мини‐футбола по теореме Пифагора:
![]() м.
м.
Ответ: 20.
5. Жители домов тщательно изучили современные материалы для мощения детской площадки. Было решено уложить в тех зонах, где есть риск получить травму, современное резиновое бесшовное покрытие. Такими зонами оказались площадка для малышей (за исключением песочницы, но включая дорожку), комплекс уличных тренажёров, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. Цены на материалы и монтаж приведены в таблице.
|
Площадь (м2) |
менее 100 |
100‐250 |
250‐500 |
более 500 |
|
Цена (руб./м2) |
1500 |
1470 |
1430 |
1400 |
Заказ на все площадки делается одновременно, и стоимость заказа зависит от суммарной площади. На сколько рублей дороже оказалось покрыть площадку для малышей, чем площадку для школьников?
Решение. Площадь, которую необходимо покрыть на площадке для малышей, равна
![]() м2.
м2.
Площадь, которую необходимо покрыть на площадке для школьников, равна
![]() м2.
м2.
Суммарная площадь составляет 344 + 316 = 660 м2, поэтому цена 1 м2 покрытия составит 1400 руб.
Стоимость покрытия площадки для малышей равна
![]() руб.
руб.
Стоимость покрытия площадки для школьников равна
![]() руб.
руб.
Разница в стоимости составляет ![]() руб.
руб.
Ответ: 39 200.
6. Найдите значение выражения ![]()
Решение. Вычислим:
![]()
Ответ: 2,8.
7. На координатной прямой точками A, B, C и D отмечены числа −0,74; −0,047; 0,07; −0,407. Какой точкой изображается число −0,047?
В ответе укажите номер правильного варианта.
![]()
1) A
2) B
3) C
4) D
Решение. Заметим, что ![]() Следовательно, числу −0,047 соответствует вторая справа точка то есть точка C.
Следовательно, числу −0,047 соответствует вторая справа точка то есть точка C.
Правильный ответ указан под номером: 3.
8. Найдите значение выражения ![]() при x = −13.
при x = −13.
Решение. Преобразуем выражение:
![]()
Подставим значение ![]()
![]()
Ответ: 0,3.
9. Решите уравнение ![]() .
.
Решение. Последовательно получаем:
![]()
![]()
Ответ: 2,5.
10. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Решение. Всего выступает 13 + 2 + 5 = 20 спортсменов. Из них не из России 7 спортсменов. Поэтому вероятность того, что первым будет стартовать спортсмен не из России равна ![]()
11. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) ![]()
Б) ![]()
B) ![]()
ГРАФИКИ
|
1)
|
2)
|
3)
|
В таблице под каждой буквой укажите соответствующий номер.
Решение. Определим вид графика каждой из функций:
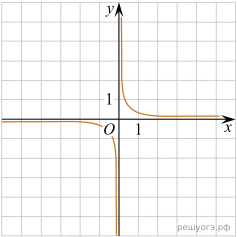
А) ![]() — уравнение гиперболы
— уравнение гиперболы
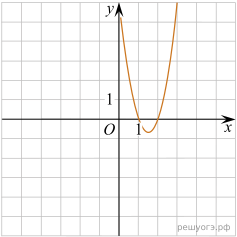
Б) ![]() — уравнение параболы, ветви которой направлены вверх
— уравнение параболы, ветви которой направлены вверх
B) ![]() — уравнение прямой
— уравнение прямой
Найдём для каждого графика функцию: A — 3, Б — 1, В — 2.
Ответ: 312.
12. Площадь четырёхугольника можно вычислить по формуле ![]() где
где ![]() и
и ![]() — длины диагоналей четырёхугольника,
— длины диагоналей четырёхугольника, ![]() — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали ![]() если
если ![]()
![]() a
a ![]()
Решение. Выразим длину диагонали ![]() из формулы для площади четырёхугольника:
из формулы для площади четырёхугольника:
![]()
Подставляя, получаем:
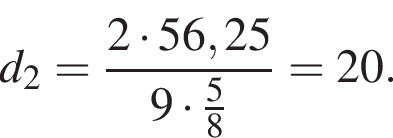
Ответ: 20.
13. На каком рисунке изображено множество решений неравенства ![]() ?
?
В ответе укажите номер правильного варианта.
|
1)
|
2)
|
|
3)
|
4)
|
Решение. Решим неравенство: ![]() Корнями уравнения
Корнями уравнения ![]() являются числа -1 и 4. Поэтому
являются числа -1 и 4. Поэтому
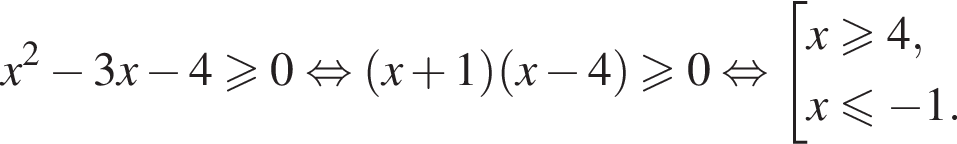
Множество решений неравенства изображено на рис. 2.
Правильный ответ указан под номером 2.
14. При проведении химической реакции в растворе образуется нерастворимый осадок. Наблюдения показали, что каждую минуту образуется 0,5 г осадка. Найдите массу осадка (в граммах) в растворе спустя восемь минут после начала реакции.
Решение. Масса осадка в растворе спустя восемь минут после начала реакции:
![]() г.
г.
Ответ: 4.
15.  В треугольнике ABC известно, что
В треугольнике ABC известно, что ![]() , AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Решение. Поскольку AD – биссектриса, то ![]() . Таким образом,
. Таким образом, ![]()
Ответ: 21
16.
Касательные в точках A и B к окружности с центром O пересекаются под углом 38°. Найдите угол ABO. Ответ дайте в градусах.
Решение.  Введём обозначение, как показано на рисунке. Касательные, проведённые к окружности из одной точки равны, поэтому
Введём обозначение, как показано на рисунке. Касательные, проведённые к окружности из одной точки равны, поэтому ![]() следовательно, треугольник ABC — равнобедренный. Откуда
следовательно, треугольник ABC — равнобедренный. Откуда ![]() Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга AB равна 142°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 142°. Рассмотрим треугольник AOB, он равнобедренный, следовательно,
Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга AB равна 142°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 142°. Рассмотрим треугольник AOB, он равнобедренный, следовательно, ![]()
Ответ: 19.
17.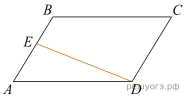
Площадь параллелограмма ABCD равна 70. Точка E — середина стороны AB. Найдите площадь трапеции EBCD.
Решение. Диагональ параллелограмма делит его на два равных треугольника, поэтому ![]() Медиана треугольника делит его на два равновеликих треугольника, поэтому
Медиана треугольника делит его на два равновеликих треугольника, поэтому ![]() Следовательно,
Следовательно,
![]()
Ответ: 52,5.
18.
На рисунке изображен параллелограмм ABCD. Используя рисунок, найдите ![]() .
.
Решение. Синус угла в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе. Треугольник BAH — прямоугольный, поэтому ![]()
Вычислим по теореме Пифагора длину гипотенузы AB:
![]()
Тогда
![]()
Ответ: 0,6.
19. Какое из следующих утверждений верно?
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Смежные углы равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение. 1) «Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой» — верно, это аксиома планиметрии.
2) «Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны» — неверно: например, могут быть квадрат и ромб с равной длиной стороны.
3) «Смежные углы равны» — неверно, смежные углы ![]() и
и ![]() связаны соотношением:
связаны соотношением: ![]() .
.
Ответ: 1.
20. Решите уравнение ![]()
Решение. Преобразуем уравнение:
![]()
![]()
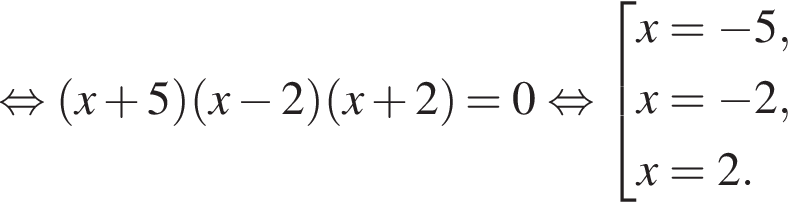
Ответ: −5; −2; 2.
21. От пристани А к пристани В, расстояние между которыми равно 280 км, отправился с постоянной скоростью первый теплоход, а через 4 часа после этого следом за ним, со скоростью, на 8 км/ч большей, чем у первого, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.
Решение. Пусть x км/ч — скорость первого теплохода, тогда ![]() км/ч — скорость второго теплохода. Расстояние между пристанями 280 км, второй теплоход отправился в путь через 4 часа после выхода первого, причём в конечный пункт оба теплохода прибыли одновременно, составим уравнение:
км/ч — скорость второго теплохода. Расстояние между пристанями 280 км, второй теплоход отправился в путь через 4 часа после выхода первого, причём в конечный пункт оба теплохода прибыли одновременно, составим уравнение:
![]()
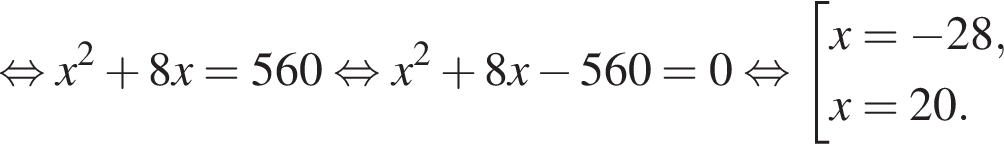
Корень −28 не подходит по условию задачи, следовательно, скорость первого теплохода равна 20 км/ч.
Ответ: 20.
22. Постройте график функции
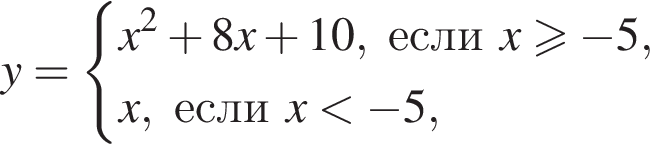
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Решение. Построим график функции y = x при x y = x2 + 8x + 10 при x ≥ −5.
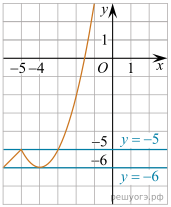
Прямая y = m имеет с графиком ровно две общие точки при m = −5 и m = −6.
Ответ: −5; −6.
23. В прямоугольном треугольнике ABC с прямым углом C известны катеты: ![]() ,
, ![]() . Найдите медиану CK этого треугольника.
. Найдите медиану CK этого треугольника.
Решение.  Медиана, проведенная к гипотенузе, равна её половине:
Медиана, проведенная к гипотенузе, равна её половине:
![]()
Ответ: 5.
24. 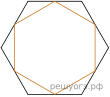 Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Решение.  Рассмотрим маленькие треугольники
Рассмотрим маленькие треугольники ![]() и
и ![]()
![]() ,
, ![]() следовательно, эти треугольники равны по двум сторонам и углу. Аналогично равны между собой и остальные маленькие треугольники. Следовательно,
следовательно, эти треугольники равны по двум сторонам и углу. Аналогично равны между собой и остальные маленькие треугольники. Следовательно, ![]()
Любой угол правильного шестиугольника равен ![]() Треугольники
Треугольники ![]() и
и ![]() — равнобедренные, углы при основаниях равны
— равнобедренные, углы при основаниях равны ![]() Рассмотрим развёрнутый угол
Рассмотрим развёрнутый угол ![]()
![]()
![]()
Аналогично все остальные углы шестиугольника ![]() равны
равны ![]() следовательно, шестиугольник
следовательно, шестиугольник ![]() — правильный.
— правильный.
25. В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 15 и 7. Найдите площадь параллелограмма ABCD.
Решение.  Проведём построения и введём обозначения, как показано на рисунке. Пусть O — центр окружности, вписанной в треугольник
Проведём построения и введём обозначения, как показано на рисунке. Пусть O — центр окружности, вписанной в треугольник ![]() Центр вписанной окружности — это точка пересечения биссектрис, поэтому
Центр вписанной окружности — это точка пересечения биссектрис, поэтому ![]() — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём
— биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём ![]()
![]()
Отрезки ![]() и OK равны как радиусы вписанной в треугольник ABC окружности, то есть
и OK равны как радиусы вписанной в треугольник ABC окружности, то есть ![]() Рассмотрим треугольники ALO и AOK, они прямоугольные, углы LAO и OAK равны, AO — общая, следовательно, треугольники равны, откуда
Рассмотрим треугольники ALO и AOK, они прямоугольные, углы LAO и OAK равны, AO — общая, следовательно, треугольники равны, откуда ![]() Аналогично из равенства треугольников COM и COK получаем
Аналогично из равенства треугольников COM и COK получаем ![]() а из равенства треугольников BOL и BOM —
а из равенства треугольников BOL и BOM — ![]() Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
![]()
![]()
![]()
Площадь параллелограмма равна произведению высоты на основание:
![]()
![]()
Рассмотрим треугольники ABC и ACD, AB равно CD, AD равно BC, углы ABC и ADC равны, следовательно, треугольники ABC и ACD равны. Поэтому площадь треугольника ABC равна половине площади параллелограмма:
![]()
![]()
Площадь параллелограмма равна: ![]()
Ответ: 924
|
№ задания |
ответ |
|
1 |
8437 |
|
2 |
3,2 |
|
3 |
48 |
|
4 |
20 |
|
5 |
39 200 |
|
6 |
2,8 |
|
7 |
3 |
|
8 |
0,3 |
|
9 |
2,5 |
|
10 |
0,35 |
|
11 |
312 |
|
12 |
20 |
|
13 |
2 |
|
14 |
4 |
|
15 |
21 |
|
16 |
19 |
|
17 |
52,5 |
|
18 |
0,6 |
|
19 |
1 |
|
20 |
−5; −2; 2 |
|
21 |
20 |
|
22 |
−5; −6 |
|
23 |
5 |
|
24 |
– |
|
25 |
924 |
ОГЭ математика
75 вариант
1. Для объектов, указанных в таблице, определите, какими цифрами они
обозначены на схеме. Заполните таблицу, в ответ запишите последовательность
четырёх цифр.
|
Объекты |
Качели |
Поле для |
Верёвочный |
Песочница |
|
Цифры |

На плане (см. рисунок) изображена детская площадка, расположенная
в общем дворе двух многоквартирных домов (сторона самой маленькой клетки на
плане равна 1 м). Площадка предназначена как для детей младшего возраста,
так и для школьников, поэтому она разделена на две отдельные части. При этом по
краю зоны для малышей есть специальная дорожка, по которой можно кататься на
роликах, машинках, велосипедах и просто бегать. Прямо перед скамейкой
расположился игровой комплекс с горкой, домиком, лесенками, а слева от скамейки
находится песочница, площадь которой равна 16 м2. Карусель
отмечена на плане цифрой 6. Кроме того, в зоне для малышей имеются качели. В
зоне для школьников находятся: комплекс уличных тренажёров, обозначенный цифрой
1, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. При
этом поле для мини‐футбола имеет самую большую площадь, а верёвочный
комплекс — самую маленькую.
2. Сколько кубических метров песка понадобилось, чтобы слой песка в
песочнице был 20 см?
3. Найдите площадь (в м2), игрового комплекса для малышей.
4. Найдите длину (в метрах) диагонали поля для мини‐футбола.
5. Жители домов тщательно изучили современные материалы для мощения
детской площадки. Было решено уложить в тех зонах, где есть риск получить
травму, современное резиновое бесшовное покрытие. Такими зонами оказались
площадка для малышей (за исключением песочницы, но включая дорожку), комплекс
уличных тренажёров, площадка для активных игр, поле для мини‐футбола и верёвочный
комплекс. Цены на материалы и монтаж приведены в таблице.
|
Площадь (м2) |
менее 100 |
100‐250 |
250‐500 |
более 500 |
|
Цена (руб./м2) |
1500 |
1470 |
1430 |
1400 |
Заказ на все площадки делается одновременно, и стоимость заказа
зависит от суммарной площади. На сколько рублей дороже оказалось покрыть
площадку для малышей, чем площадку для школьников?
6. Найдите значение выражения ![]()
7. На координатной прямой отмечено число a.

Какое из утверждений относительно этого числа является верным?
1) a − 8 > 0
2) 7 − a < 0
3) a − 3 > 0
4) 2 − a > 0
8. Найдите значение выражения ![]()
9. Решите уравнение ![]()
Если
корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Какова вероятность того, что случайно выбранное натуральное число
от 192 до 211 включительно делится на 5?
11. Найдите значение ![]() по графику функции
по графику функции ![]() изображенному на рисунке.
изображенному на рисунке.

12. Площадь четырёхугольника можно вычислить по формуле ![]() где
где ![]() и
и ![]() —
—
длины диагоналей четырёхугольника, ![]() — угол между диагоналями.
— угол между диагоналями.
Пользуясь этой формулой, найдите длину диагонали ![]() если
если ![]()
![]() a
a ![]()
13. При каких значениях x значение выражения 9x +
7 меньше значения выражения 8x − 3?
В
ответе укажите номер правильного варианта.
1) x > 4
2) x < 4
3) x > − 10
4) x < − 10
14. За изготовление и установку нижнего железобетонного кольца колодца
заплатили 234 рубля, а за каждое следующее кольцо платили на 18 рублей меньше,
чем за предыдущее. Кроме того, по окончании работы была выплачена премия 360
рублей. Средняя стоимость изготовления и установки одного кольца с учетом
премии оказалась равна 202 рубля. Сколько колец было установлено?
15.
В выпуклом четырехугольнике ABCD известно,
что ![]() ,
, ![]() ,
, ![]() ,
, ![]() Найдите угол A. Ответ
Найдите угол A. Ответ
дайте в градусах.
16.  К окружности с центром в точке О проведены
К окружности с центром в точке О проведены
касательная AB и секущая AO. Найдите радиус
окружности, если AB = 65 , AO = 97 .
17.  Высота BH параллелограмма ABCD делит
Высота BH параллелограмма ABCD делит
его сторону AD на отрезки AH = 8 и HD = 28.
Диагональ параллелограмма BD равна 35. Найдите площадь параллелограмма.
18.
На клетчатой бумаге с размером клетки 1х1 изображена фигура.
Найдите её площадь.
19. Какое из следующих утверждений верно?
1) Диагональ трапеции делит её на два равных треугольника.
2) Косинус острого угла прямоугольного треугольника равен
отношению гипотенузы к прилежащему к этому углу катету.
3) Расстояние от точки, лежащей на окружности, до центра
окружности равно радиусу.
В
ответ запишите номер выбранного утверждения.
20. Решите систему уравнений 
21. Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты
различной концентрации. Если их слить вместе, то получится раствор, содержащий
40 % кислоты. Если же слить равные массы этих растворов, то полученный раствор
будет содержать 37 % кислоты. Сколько процентов кислоты содержится во втором
растворе?
22. Постройте график функции ![]() Какое наибольшее число общих
Какое наибольшее число общих
точек график данной функции может иметь с прямой, параллельной оси абсцисс?
23.
В треугольнике АВС углы А и С равны
30° и 50° соответственно. Найдите угол между высотой ВН и
биссектрисой BD.
24. В параллелограмме ABCD диагонали AC и BD пересекаются
в точке K. Докажите, что площадь параллелограмма ABCD в
четыре раза больше площади треугольника AKB.
25. В равнобедренную трапецию, периметр которой равен 120, а площадь
равна 540, можно вписать окружность. Найдите расстояние от точки пересечения
диагоналей трапеции до её меньшего основания.
|
№ п/п |
Ответ |
|
1 |
8437 |
|
2 |
3,2 |
|
3 |
48 |
|
4 |
20 |
|
5 |
39200 |
|
6 |
2,2 |
|
7 |
3 |
|
8 |
42 |
|
9 |
-66 |
|
10 |
0,2 |
|
11 |
4 |
|
12 |
14 |
|
13 |
4 |
|
14 |
9 |
|
15 |
8 |
|
16 |
72 |
|
17 |
756 |
|
18 |
10 |
|
19 |
3 |
|
20 |
|
|
21 |
55. |
|
22 |
4. |
|
23 |
10°. |
|
24 |
1,8. |