Привет! Цель нашего проекта помочь тебе подготовиться к ЕГЭ (или ОГЭ).
У нас более 1000 заданий с подробным решением, сервис, запоминающий твои ответы, и удивительная система тестирования.
Обо всем по порядку расскажу тебе после быстрой регистрации.
Присоединиться к ExamMe
ЕГЭ по Математике (профильный)
Найдите длину диагонали…
Задание:
Найдите длину диагонали прямоугольника, вершины которого имеют координаты $(2; 1), (2; 4), (6; 1), (6; 4)$.
Решение:
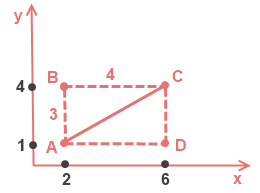
Для наглядности начертим и обозначим вершины этого прямоугольника (см. рисунок). А(2; 1), B(2; 4), D(6; 1), C(6; 4).
Найдем длину стороны $AB = 4-1 = 3$
Найдем длину стороны $BC = 6-2 = 4$
По теореме Пифагора вычислим диагональ AC.
[AC^2=AB^2+BC^2][AC=sqrt{3^2+4^2}][AC=sqrt{9+16}=sqrt{25}=5]
Ответ:
5
Задание добавил(а)
![]()
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Профильный уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
Как рассчитать диагональ прямоугольника
Замкнутая геометрическая фигура, образованная двумя парами лежащих друг напротив друга параллельных отрезков одинаковой длины, называется параллелограммом. А параллелограмм, все углы которого равны 90°, называют еще и прямоугольником. В этой фигуре можно провести два отрезка одинаковой длины, соединяющих противоположные вершины – диагонали. Длина этих диагоналей вычисляется несколькими способами.
Инструкция
Если известны длины двух смежных сторон прямоугольника (А и В), то длину диагонали (С) определить очень просто. Исходите из того, что диагональ лежит напротив прямого угла в треугольнике, образуемом ею и этими двумя сторонами. Это позволяет применить в расчетах теорему Пифагора и вычислить длину диагонали, найдя квадратный корень из суммы возведенных в квадрат длин известных сторон: С=v(А?+В?).
Если известна длина лишь одной стороны прямоугольника (А), а также величина угла (?), который с ней образует диагональ, то для вычисления длины этой диагонали (С) придется использовать одну из прямых тригонометрических функций – косинус. Разделите длину известной стороны на косинус известного угла – это и будет искомая длина диагонали: С=А/cos(?).
Если прямоугольник задан координатами своих вершин, то задача вычисления длины его диагонали сведется к нахождению расстояния между двумя точками в этой системе координат. Примените теорему Пифагора к треугольнику, который образуют проекции диагонали на каждую из координатных осей. Допустим, прямоугольник в двухмерных координатах образован вершинами A(X?;Y?), B(X?;Y?), C(X?;Y?) и D(X?;Y?). Тогда вам нужно вычислить расстояние между точками A и C. Длина проекции этого отрезка на ось X будет равна модулю разности координат |X?-X?|, а проекции на ось Y – |Y?-Y?|. Угол между осями равен 90°, из чего вытекает, что эти две проекции являются катетами, а длина диагонали (гипотенузы) равна квадратному корню из суммы квадратов их длин: AC=v((X?-X?)?+(Y?-Y?)?).
Для нахождения диагонали прямоугольника в трехмерной системе координат действуйте так же, как в предыдущем шаге, лишь добавив в формулу длину проекции на третью координатную ось: AC=v((X?-X?)?+(Y?-Y?)?+(Z?-Z?)?).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Условие
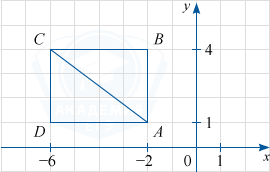
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (-2; 1), (-2; 4), (-6; 1), (-6; 4).
Показать решение
Решение
Диагонали прямоугольника равны. Диагональ AC найдём как гипотенузу прямоугольного треугольника ADC с катетами AD=4, CD=3:
AC=sqrt{AD^2+CD^2}=sqrt{4^2+3^2}=5
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Рассказать друзьям
Лучшие онлайн-курсы для подготовки к ЕГЭ
Лучшие репетиторы для сдачи ЕГЭ
Комментарии
Задавайте ваши вопросы и помогайте друг другу в решении задач
Комментарии содержащие в себе рекламу, нецензурную лексику и не относящиеся к тематике сайта будут удалены
Лучшие репетиторы для сдачи ЕГЭ
Нахождение длины вектора, примеры и решения
Длина вектора – основные формулы
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
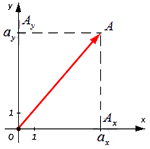
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
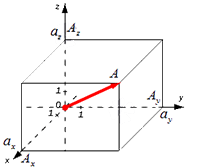
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Вычислить длину вектора a → = 4 · i → – 3 · j → + 5 · k → , где i → , j → , k → – орты прямоугольной системы координат.
Дано разложение вектора a → = 4 · i → – 3 · j → + 5 · k → , его координаты равны a → = 4 , – 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( – 3 ) 2 + 5 2 = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x – a x ; b y – a y ) значит, его длина может быть определена по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2
А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B – 3 , 1 .
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x – a x ) 2 + ( b y – a y ) 2 : A B → = ( – 3 – 1 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( – 3 – 1 ; 1 – 3 ) = ( – 4 ; 1 – 3 ) ; A B → = ( – 4 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 . –
Ответ: A B → = 20 – 2 3 .
Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .
Для начала распишем длину вектора A B → по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 = ( 5 – 0 ) 2 + ( 2 – 1 ) 2 + ( λ 2 – 2 ) 2 = 26 + ( λ 2 – 2 ) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :
26 + ( λ 2 – 2 ) 2 = 30 26 + ( λ 2 – 2 ) 2 = 30 ( λ 2 – 2 ) 2 = 4 λ 2 – 2 = 2 и л и λ 2 – 2 = – 2 λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 – 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 – 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x – a x ) 2 + ( b y – a y ) 2 или A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 , в некоторых случаях следует использовать теорему косинусов.
Длина вектора — основные формулы
Время чтения: 16 минут
Основные понятия вектора
Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора – отрезок который имеет указание направления в виде стрелки.
Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
- Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
- Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.
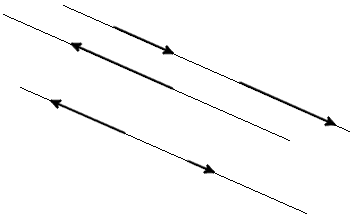
- Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
- Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
- Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
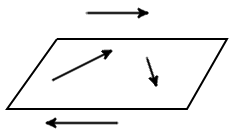
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Как найти длину вектора
Модуль вектора а будем обозначать  .
.
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор  имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора
имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора  , через известные нам координаты aₓ и aᵧ.
, через известные нам координаты aₓ и aᵧ.
На взятой системе координат, от её начала отложим вектор
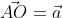 В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
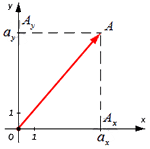
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
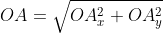
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 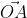 получаем
получаем
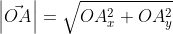
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:

Когда вектор  дан в формате разложения по координатным векторам
дан в формате разложения по координатным векторам 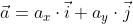 , то вычислить его можно по той же формуле
, то вычислить его можно по той же формуле  , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат
, в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат  , в данной системе координат.
, в данной системе координат.
Чтобы рассчитать длину  = (3, √x), расположенного в прямоугольной системе координат.
= (3, √x), расположенного в прямоугольной системе координат.
Чтобы найти модуль вектора используем ранее приведённую формулу

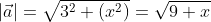
Ответ: 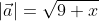
Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор  =(aₓ ; aᵧ ; a
=(aₓ ; aᵧ ; a  )
)
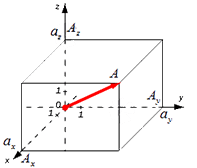
В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО – диагональ прямоугольного параллелепипеда), поэтому
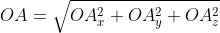
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA =a
=a  , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
, а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
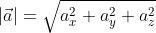
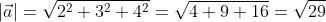
Ответ: 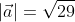
Длина вектора через координаты точек начала и конца
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор  имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
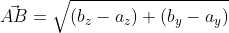
При этом формула вычисления длины вектора  для трёхмерного пространства, с координатами
для трёхмерного пространства, с координатами 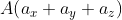 и
и 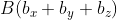 ), будет следующей:
), будет следующей:
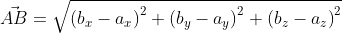
Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
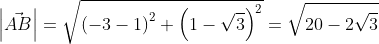
Существует второй вариант решения, где формулы применяются по очереди:
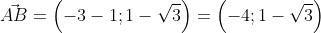
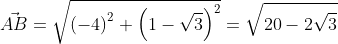
Ответ: 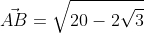
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))
В первую очередь представим длину вектора в виде формулы.
( left|vecright|=sqrt<left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2>)
(=sqrt <left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2>= sqrt<26 + left ( lambda^2 -2right )^2>)
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
( sqrt<26+left(lambda^2-2right)^2>=sqrt <30>)
( 26+left(lambda^2-2right)^2=30 )
( left(lambda^2-2right)^2=4 )
( lambda^2-2=2 ) или ( lambda^2-2=-2 ) ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Ответ: ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Длина вектора по теореме косинусов
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac<pi> <3>) . необходимо найти длину ( overrightarrow).
В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
( KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac<pi><3>)
(=2^2+4^2-2cdot2cdot4cdotcosfrac<pi><3>)
(=4+16-16cosfrac<pi><3>)
(=20-8=12 )
Получается (KM=sqrt <12>)
Ответ: ( left|overrightarrowright|=sqrt <12>)
Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.
длина вектора формула для трёхмерного пространства;
длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt<left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2>) если известны координаты начала и конца вектора на плоскости.
Существует также формула длины вектора перемещения: ( left|vecright|=sqrt< s_x^2+s_y^2>) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.

Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
[spoiler title=”источники:”]
http://www.napishem.ru/spravochnik/matematika/dlina-vektora-osnovnye-formuly.html
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
[/spoiler]
Диагональ прямоугольника делит его на два прямоугольных треугольника и является гипотенузой обеих. Чтобы найти длину, проще всего воспользоваться теоремой Пифагора, которая в нашем случае будет звучать так
Это будет основная формула, но так как не всегда в условии заданы значения сторон прямоугольника, на помощь придут другие:

И теперь на нескольких примерах решим наше задание
Пример 1
найдем длину диагонали прямоугольника, если известна его а)сторона и периметр б) сторона и площадь.
Для этого сначала найдем неизвестную сторону, затем значения обеих сторон подставим в главную формулу

Пример 2
найдем длину диагонали прямоугольника, если известны его периметр и площадь.
Для этого составим систему уравнений, решим ее и подставим значения сторон в основную формулу

Пример 3
нужно найти длину диагонали прямоугольника, если известны его а)площадь и угол между диагональю и стороной б)периметр и угол между диагональю и стороной.
Решение аналогично предыдущему примеру

Как видим, без теоремы Пифагора во всех этих случаях никак не обойтись.

