Как найти диагональ ромба?
Мастер
(1719),
закрыт
15 лет назад
ezvx
Мыслитель
(9126)
15 лет назад
нет ну ты пипец. .
у ромба диагонали пересекаются под прямым углом.. . решай прямоугольные треугольники внутри теорему пифагора напомнить?
Саша Н
Просветленный
(22924)
15 лет назад
Задача на теорему Пифагора
1. половина диагонали (меньшей) – 6см. (а)
2. Строна -10 см. (с)
3. Половина другой диагонали – (в) = корень кв. из ( с в квадрате – а в квадрате)
в= корень (10*10-6*6) = 8
4. значит вся диагональ – 8*2 =16…
вот и все!
Rasamaxa
Гуру
(4191)
15 лет назад
Диагонали пересекаются у ромба, и точка их пересечения делит их пополам. Следовательно в прямоугольном треугольнике, у которого гипотенуза равна 10см, один катет 12/2 = 6см, то по тиореме пифагора 10*10 = 6*6+х*х, где х – второй катет, отсюда получаем что х*х = 64, то х = 8, а так как х является половиной искомой диагонали, то вся диагональ равна 2*х=2*8=16см.
Dancer
Профи
(521)
15 лет назад
по св-ву ромба его диагонали пересекаются под прямым углом и точкой пересечения делятся попалам,
те у тебя прямоугольный треугольник с гипотинзой 10 и катетом 6 по т-ме Пифагора получаем другой катет 8 но это 1/2 диагонали те 8*2=16
Диагональ параллелограмма – это отрезок, соединяющий противоположные вершины фигуры. В зависимости от
вида геометрической фигуры диагональ обладает важными свойствами, на которые основываются базовые
правила и формулы. Рассмотрим подробнее, как найти длину данного отрезка, построенного в
параллелограмме с равными сторонами, т.е. ромбе.
- Диагональ ромба через сторону и другую известную
диагональ - Длинная диагональ ромба через сторону и острый угол
- Длинная диагональ ромба через сторону и тупой угол
- Короткая диагональ ромба через сторону и острый угол
- Короткая диагональ ромба через сторону и тупой угол
- Длинная диагональ ромба через короткую диагональ и тупой
угол - Короткая диагональ ромба через длинную диагональ и острый
угол - Диагональ ромба через площадь ромба и другую известную
диагональ
Диагональ ромба через сторону и другую известную диагональ
В случае, если в ромбе известны значения одной диагонали (d) и стороны (a) фигуры, прийти к
определению длины второго отрезка будет несложно, благодаря тождеству параллелограмма, которое
гласит, что сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:
d = √(4a² — d²)
где a — сторона, d — известная диагональ.
Цифр после
запятой:
Результат в:
Пример. Дан ромб с диагональю равной 6 мм и стороной, длина которой 5 мм. Нужно
найти вторую диагональ ромба. d = √(4 * 5² — 6²) = √(4 * 25 — 36) = √(100 — 36) = √64 = 8 мм
– длина неизвестной диагонали.
Как найти длину большей диагонали через сторону и острый угол
Найти величину длинной диагонали можно по формуле:
d = a * √(2 + 2 * cos α)
где a — сторона, cos α — острый угол.
Цифр после
запятой:
Результат в:
Проведенный отрезок, который соединяет противоположные вершины фигуры, делит ее на равнобедренные
треугольники. По свойствам равнобедренного треугольника косинус углов при основании равен половине
основания (в данном случае диагонали), деленного на боковую сторону (сторону ромба).
Пример. Острый угол между сторонами ромба длиной 6 см равен 45 градусам. Найти
биссектрису острого угла ромба (в данном случае диагональ). d = 6 * √(2 + 2 * cos 45°) = 6 * √(2 + 2 * √2 / 2) = 6 * √(2 + 2 * 0,7) = 11см
– длинна неизвестного отрезка.
Как найти длину большей диагонали через сторону и известное значение тупого угла
Как уже известно, построенная диагональ в ромбе, делит его на 2 равнобедренных треугольника. Если
дополнить картину второй проведенной диагональю, получится прямоугольный треугольник. Косинус
половинки тупого угла (c) это отношение прилежащего катета к гипотенузе (стороне ромба a). На
основании всех этих свойств можно прийти к простой формуле нахождения нужной диагонали через сторону
ромба (в данном случае гипотенузу) и косинус тупого угла:
d = a * √( 2 — 2 * cos β)
где a — сторона, cos β — тупой угол
Цифр после
запятой:
Результат в:
Пример. Дан ромб со стороной 4,65 м, величина тупого угла которого равна 120
градусам. Необходимо найти противолежащую известному углу диагональ. d = 4,65 * √(2 — 2 * cos 120°) = 4,65 * √(2 — 2 * (-0,5) = 8 м
– длина неизвестного отрезка.
Как вычислить длину меньшей диагонали через сторону и острый угол
Так как ситуация аналогична предыдущей (только известный противолежащий угол острый), формула
нахождения короткой диагонали практически ничем не отличается от алгоритма определения длинного
отрезка, соединяющего противолежащие вершины ромба.
d = a * √(2 — 2 * cos α)
где a — сторона, cos α — острый угол
Цифр после
запятой:
Результат в:
Пример. В ромбе со стороной 4,65 м проведена диагональ, которая является основанием
равнобедренного треугольника с углом при вершине равным 52 градусам. Найти основание треугольника
(меньшую диагональ). d = 4,65 * √(2 — 2 * cos 52°) = 4 м.
Короткая диагональ ромба через длинную диагональ и острый угол
Аналогично с предыдущей ситуацией, через тангенс острого угла находим величину неизвестного катета
(половинку искомой диагонали). Упрощенная формула:
d = D * tg (α / 2)
где D — длинная диагональ, α — острый угол
Цифр после
запятой:
Результат в:
Пример. Острый угол ромба, в котором построена диагональ длиной 11 мм, равен 58
градусам. Найти длину второй диагонали. d = 11 * tg 29° = 6 мм – длина
меньшей диагонали ромба.
Короткая диагональ через сторону и тупой угол
Формула для нахождения меньшей диагонали ромба при помощи значения стороны и тупого угла такова:
d = a * √(2 + 2 * cos β)
где a — сторона, cos β — тупой угол
Цифр после
запятой:
Результат в:
Пример. Дан ромб со стороной 4,65 мм, один из углов которого равен 128 градусов, а
меньшая диагональ фигуры – искомая величина. d = a * √(2 + 2 * cos β) = 4,65 * √(2 + 2 * cos 128°) = 4 мм.
Длинная диагональ ромба через короткую диагональ и тупой угол
Длина большей диагонали ромба легко находится по формуле:
D = d * tg (β / 2)
где d — короткая диагональ, β — тупой угол
Цифр после
запятой:
Результат в:
Благодаря теореме Пифагора, зная длину короткой диагонали (половина катета прямоугольного
треугольника) и значение тупого угла ромба (половина которого является углом прямоугольного
треугольника), не составит труда определить значение большей диагонали ромба через тангенс тупого
угла.
Пример. Дан ромб с диагональю 6,5 см, которая является биссектрисой тупого угла
величиной 119 градусов. Нужно найти неизвестную диагональ ромба. D = 6,5 * tg (119 / 2) = 11 см
– искомая величина.
Диагональ ромба через площадь и другую известную диагональ
Найти любую из двух диагоналей ромба можно по формуле:
D = 2 * S / d
где d – длина известного отрезка, а S-площадь фигуры.
Цифр после
запятой:
Результат в:
Пример. Дан ромб с площадью равной 64 см², его диагональ равна 8,5 см. Необходимо
найти длину второго отрезка, соединяющего противолежащие вершины. D = 2 * S / d = 2 * 64 / 8,5 = 15 см.
Ромб относится к плоским выпуклым геометрическим фигурам. Данный вид параллелограмма отличается
равными сторонами, а также тем, что его диагонали при пересечении перпендикулярны друг другу.
Существуют и другие свойства ромба, которые подробно раскрывают смысл указанных выше формул:
- Диагонали, пересекаясь под прямым углом, делятся точкой пересечения пополам. Таким образом, они
всегда разделяют фигуру на 4 прямоугольных треугольника. - Противоположные стороны ромба попарно параллельны.
- Противолежащие углы равны, а смежные – в сумме образуют 180 градусов.
- Диагонали служат биссектрисами всех углов ромба.
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
- Если соединить середины сторон ромба, получится прямоугольник.
- Точка пересечения диагоналей — центр вписанной окружности.
Определение диагонали ромба часто встречается в задачах школьной программы. Найдя данное значение,
можно прийти к искомому результату задания. Через диагональ можно найти стороны ромба, площадь,
периметр и все внутренние углы ромба.
Геометрия в школьной программе включается в себя немалое количество формул, основанных на теоремах и
правилах. Некоторые из которых помогают значительно сократить время для решения задач на контрольной
или при выполнении домашней работы. Данная статья поможет быстро прийти к логическому решению
задания и правильному результату. Знание и применение выше перечисленных формул способствуют умению
решать задачи по геометрии любой сложности.
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
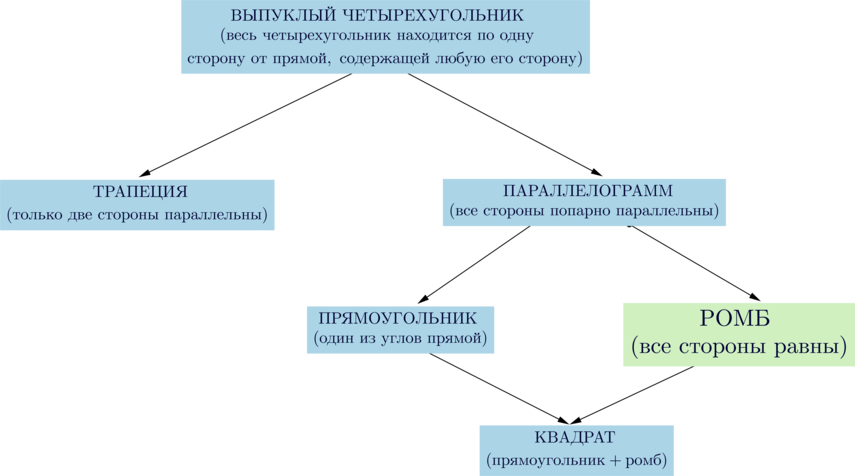
Ромб и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства ромба:
(blacktriangleright) Те же, что и у параллелограмма:
(sim) Противоположные стороны попарно равны;
(sim) Диагонали точкой пересечения делятся пополам;
(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);
(blacktriangleright) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
(blacktriangleright) все стороны равны;
(blacktriangleright) диагонали взаимно перпендикулярны и он является параллелограммом;
(blacktriangleright) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.
2. Площадь ромба равна половине произведения его диагоналей.
Задание
1
#2716
Уровень задания: Легче ЕГЭ
В ромбе (ABCD): (angle ACD = 26^{circ}). Найдите (angle ABD). Ответ дайте в градусах.
В ромбе диагонали перпендикулярны, тогда (angle CDB = 90^{circ} – angle ACD = 64^{circ}).
(BC = CD), тогда (angle CBD = angle CDB = 64^{circ}).
Так как диагонали ромба делят его углы пополам, то (angle ABD = angle CBD = 64^{circ}).
Ответ: 64
Задание
2
#2717
Уровень задания: Равен ЕГЭ
Найдите большую диагональ ромба (ABCD), если (AB = 2sqrt{3}), а острый угол равен половине тупого.
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), то сумма острого и тупого углов ромба равна (180^{circ}).
Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба (ABCD) равен (60^{circ}).
Треугольник (ABD) – равнобедренный, один из углов которого равен (60^{circ}), тогда треугольник (ABD) – равносторонний и (BD = 2sqrt{3}).
Пусть (O) – точка пересечения диагоналей ромба, тогда (OD = 0,5 BD = sqrt{3}), следовательно, по теореме Пифагора находим: (AO^2 + OD^2 = AD^2), тогда (AO^2 + 3 = 12), откуда находим (AO = 3). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, (AC = 6).
Ответ: 6
Задание
3
#2715
Уровень задания: Равен ЕГЭ
Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.
Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).
Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.
Ответ: 10
Задание
4
#1794
Уровень задания: Равен ЕГЭ
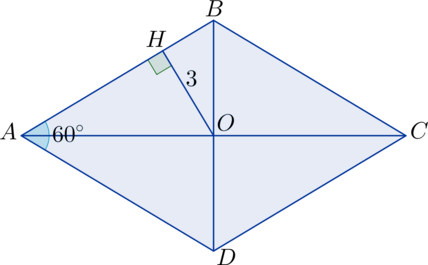
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно (3), а острый угол ромба равен (60^circ). Найдите большую диагональ ромба.
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), (angle DAB = 60^circ), тогда (angle
OAB = 30^circ). Получаем, что (OH) – катет лежащий напротив угла в (30^circ), значит (AO = 2cdot OH = 6). Т.к. (AC) и есть большая диагональ, то (AC = 2cdot AO = 12).
Ответ: 12
Задание
5
#1757
Уровень задания: Равен ЕГЭ
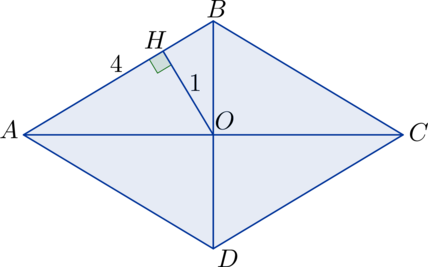
Сторона ромба равна (4). Расстояние от точки пересечения его диагоналей до одной из сторон равно (1). Найдите площадь ромба.
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), тогда (S_{triangle ABO} = frac{1}{2}cdot 1 cdot 4 = 2). Диагонали ромба делят его на (4) равных прямоугольных треугольника (Rightarrow) (S_{ABCD} = 4cdot 2 = 8).
Ответ: 8
Задание
6
#2718
Уровень задания: Равен ЕГЭ
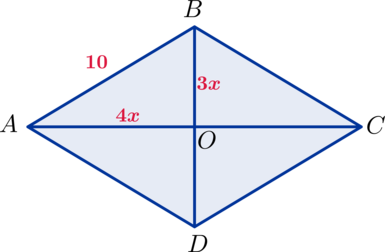
Периметр ромба равен (40), а диагонали относятся, как (3:4). Найдите площадь ромба.
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении (3:4). Зная периметр, найдем сторону ромба: (40
: 4 = 10). Сторона и половинки диагоналей образуют прямоугольный треугольник (AOB).
Пусть (AO=4x), (BO=3x).
Тогда по теореме Пифагора: ((3x)^2 + (4x)^2 = 10^2) (Rightarrow) (25x^2 = 100) (Rightarrow) (x^2 = 4) (Rightarrow) (x = 2). Диагонали равны (BD=2BO=12) и (AC=2AO=16) (Rightarrow) (S_{ABCD} =
frac{1}{2}cdot12cdot16 = 96).
Ответ: 96
Задание
7
#2719
Уровень задания: Равен ЕГЭ
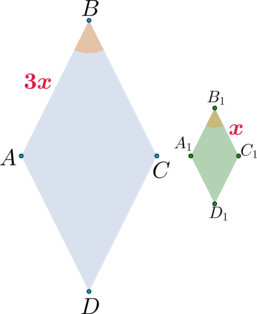
Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как (3:1)?
Пусть (angle B) и (angle B_1) – равные углы ромбов. Так как стороны ромбов относятся как (3:1), то можно обозначить их за (3x) и (x) соответственно.
Тогда и (angle D=angle D_1) (так как у ромба противоположные углы равны). Следовательно, (triangle ABCsim triangle A_1B_1C_1) и (triangle ADCsimtriangle A_1D_1C_1) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен (3). Следовательно, их площади относятся как (9:1). А так как (S_{ABC}+S_{ADC}=S_{ABCD}) и (S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}), то (S_1:S_2=9:1).
Ответ: 9
Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.
Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.
Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.
Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.
Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.

УСТАЛ? Просто отдохни
|
Начнем с того что у ромба две диагонали. Одна большая D, а другая маленькая d. Рассмотрим способы нахождения большой диагонали D.
Также D находится по площади ромба и малой диагонали: D=(2*S)/d; Рассмотрим способы нахождения меньшей диагонали d.
Малую диагональ d тоже можно найти через площадь ромба и большую диагональ: d=(2*S)/D; автор вопроса выбрал этот ответ лучшим Alexsandr82 5 лет назад У ромба есть две диаганали: большая (d1) и малая (d2), а также углы а – острый угол ромба (в ромбе два острых угла и оба равны между собой), и b – тупой угол (их тоже два и они тоже равны). Если нам известна сторона ромба (x) и один из углов то мы можем найти любую диагональ по формулам: d1 = 2x*cos(a/2) d2 = 2x*sin(a/2) Или d1 = 2x*sin(b/2) d2 = 2x*cos(b/2) Кроме этого если нам извесна площадь ромба и одна из диагоналей мы можем найти вторую диагональ по формулам: d1 = 2S/d2 d2 = 2S/d1 Если нам дан радус вписанной в ромб окружности и любой из углов мы также можем рассчитать диагональ ромба: d1 = 2r/sin(a/2) d2 = 2r/sin(b/2) Где r – радиус вписанной окружности. Знаете ответ? |
В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.
- Определение ромба
-
Свойства ромба
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Признаки ромба
Определение ромба
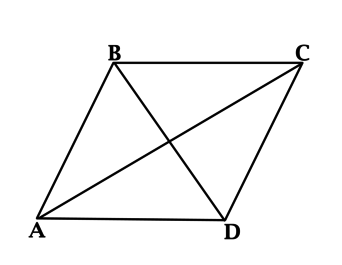
Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).
- AB = BC = CD = AD = a
- AB параллельна CD, BC параллельна AD.
Примечание: квадрат является частным случаем ромба.
Свойства ромба
Свойство 1
Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.
- ∠ABC = ∠ADC, ∠BAD = ∠BCD
- α + β = 180°
Свойство 2
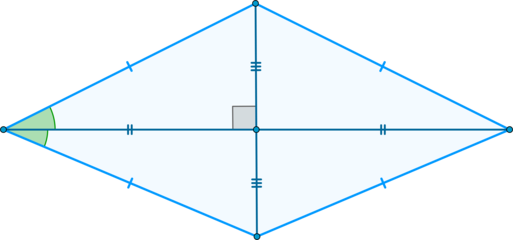
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
- диагональ BD (d1) перпендикулярна диагонали AC (d2)
- AE = EC
- BE = ED
В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.
Свойство 3
Диагонали ромба являются биссектрисами его углов.
Свойство 4
Сторону ромба a можно найти через его диагонали d1 и d2 (согласно теореме Пифагора).
- a – гипотенуза любого из 4 прямоугольных треугольников (например, ΔBEC);
- половины диагоналей d1 и d2 – катеты треугольников.
Свойство 5
В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Радиус вписанной в ромб окружности r вычисляется по формуле:
Признаки ромба
Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:
- Его диагонали пересекаются под прямым углом.
- Если его диагонали являются биссектрисами его углов.
- Две смежные стороны равны (следовательно, все стороны равны).
Примечание: Любой четырехугольник, стороны которого равны, является ромбом.