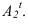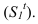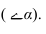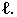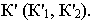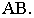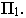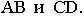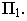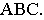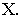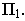Содержание:
Проекционные чертежи архитектурных объектов выполненные в одних линиях, не дают достаточно полного представления о запроектированном объекте.
Для придания объемности и наглядности ортогональным чертежам зданий и сооружений выполняется построение теней.
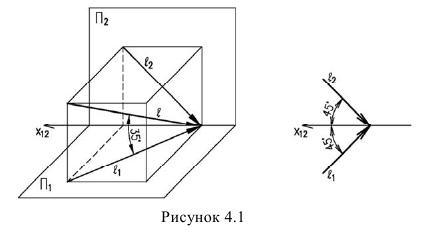
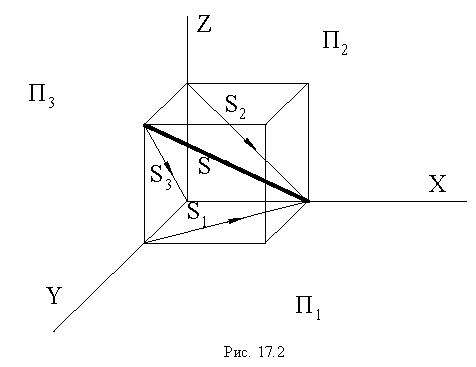
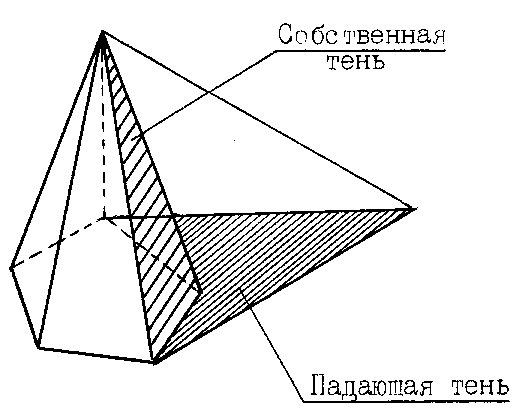
Тени строятся от естественного освещения, т.е. солнца. Так как солнце практически бесконечно удаленная точка, то лучи принимаются параллельными. За направление лучей принимается диагональ куба грани которого совпадают с плоскостями проекций, а её проекции являются диагоналями граней куба, т.е. квадратов (см. рисунок 4.1). Истинный угол наклона будет равен 35°, а проекции лучей располагаются под углом 45° к оси (см. рисунок 4.1).
Тень точки – способ следа луча, способ выноса
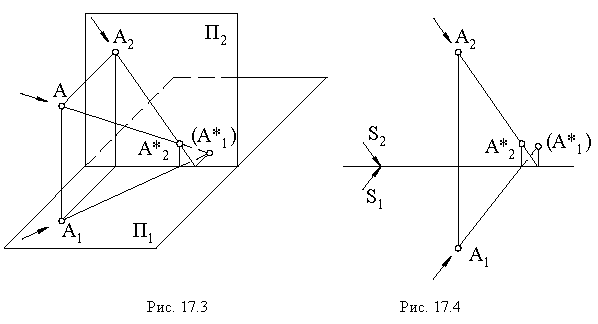
Тенью точки на плоскости является точка пересечения светового луча, проведенного через данную точку, с плоскостью. Если тень точки падает на плоскость проекций, то для её построения используется способ следа луча. Т.е. через проекции точки проводим проекции лучей и строим след. На рисунке 4.2 след луча фронтальный, следовательно тень падает на фронтальную плоскость —
Кроме этого может быть использован метод выноса. Особенно важен этот метод при построении теней на фасадах зданий.
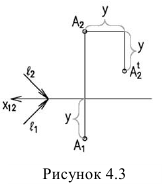
Вынос – это расстояние от точки до фронтальной плоскости или плоскости фасада, если тень строится на фасаде. На рисунке 4.3 у – эго вынос.
Тень примой общего положении
Тенью прямой на плоскость является линия пересечения лучевой плоскости, проведенной через прямую с заданной плоскостью. Т.е. тенью прямой на плоскость является прямая линия. Поэтому для построения тени прямой на плоскость, достаточно построить тени двух ее точек.
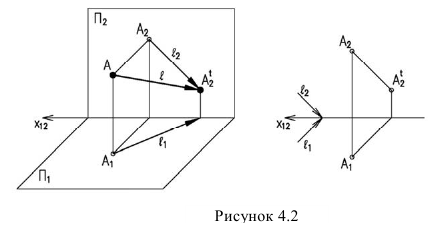
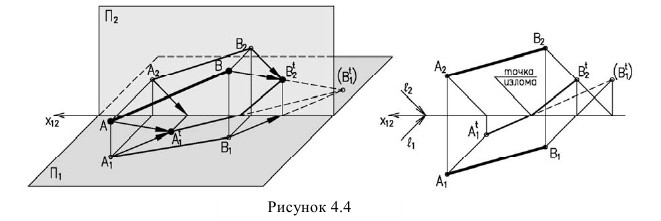
Если же тень от прямой падает на две плоскости, то она имеет точку излома, лежащую на линии пересечения плоскостей. В данном случае точка излома лежит на оси (рисунок 4.4). Для ее нахождения, необходимо строить мнимую тень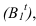
Тени прямых частного положении
Тени прямых частного положения на плоскостях проекций располагаются всегда определенно и часто служат «опорными» при построении теней различных деталей, включающих такие прямые. Рассмотрим эти случаи.
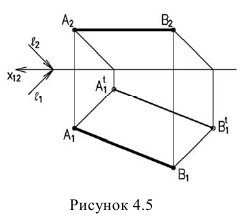
Тень от прямой, на плоскость ей параллельную, располагается параллельно прямой, т.е. параллельно проекции прямой на эту плоскость и равна ей по величине (рисунок 4.5).
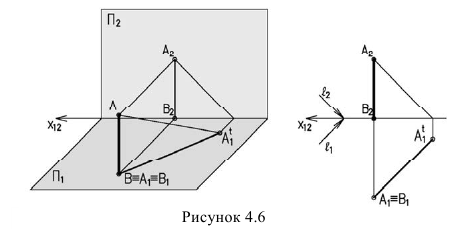
Тень от прямой на плоскость, ей перпендикулярную, располагается по проекции луча, т.е. под углом 45° (рисунок 4.6).
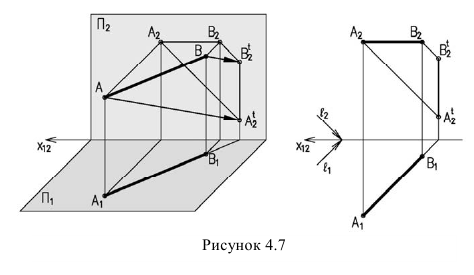
Если точка лежит на плоскости, то тень совпадает с самой точкой и такая точка называется сама себе тень. В нашем случае это точка В. Тень на фронтальной плоскости от горизонтальной прямой, расположенной под углом 45° к ней, вертикальна (рисунок 4.7)
Тени плоских фигур
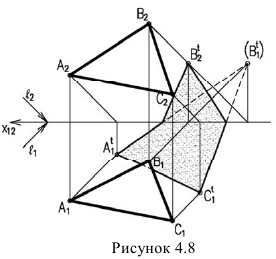
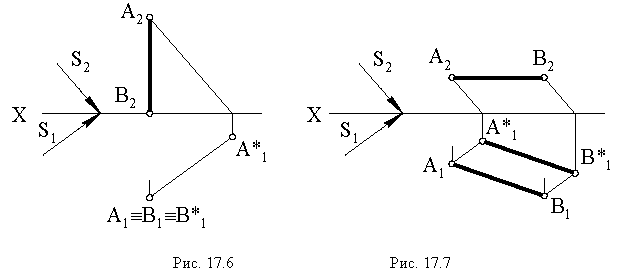
Чтобы построить тень от плоской фигуры, например треугольника, падающую на плоскости проекций достаточно построить тени от вершин (рисунок 4.8). Т.к. тень падает на две плоскости необходимо определять линию излома тени, а, следовательно, построить мнимую тень от вершины В.
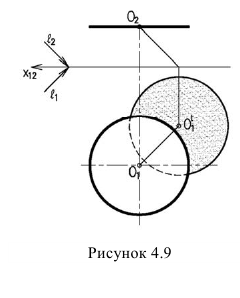
Тень от плоской фигуры, на плоскость ей параллельную, изображается фигурой равной ей по величине. Поэтому достаточно построить тень от одной точки и вычертить тень в виде той же фигуры. Так, для построения тени от окружности (рисунок 4.9) достаточно определить тень от центра и вычертить тень в виде такой же окружности.
Тень окружности
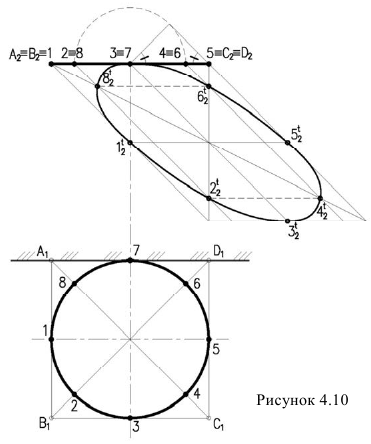
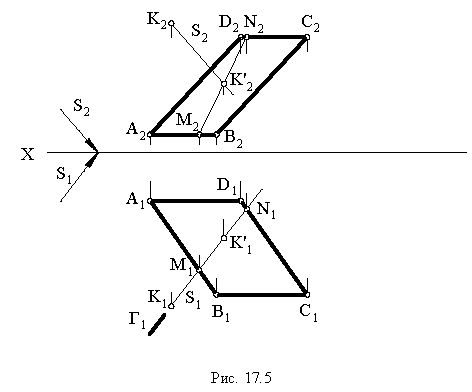
Тень окружности обычно строится по восьми точкам. Из них четыре -точки касания окружности к сторонам описанного около окружности квадрата, и четыре – точки пересечения окружности с диагоналями этого квадрата (рисунок 4.10).
Тень от квадрата – параллелограмм, диагональ которого BD вертикальна. Точки 1,3,5,7 точки касания к параллелограмму. Точки, лежащие на диагоналях, делят радиус в отношении 0,707. Они могут быть получены без горизонтальной проекции. Для этого на
радиусе строим равнобедренный треугольник с углами при основании 45° и дугой окружности определяем положение точек 2,8 и 4,6. Проведем из них лучи до пересечения с диагоналями. Полученные восемь точек соединяем плавной линией, которая будет эллипсом. Практически тень окружности по восьми точкам строят без горизонтальной проекции, которая здесь приведена только для пояснения.
Тени поверхностей. Понятие собственной и падающей тени
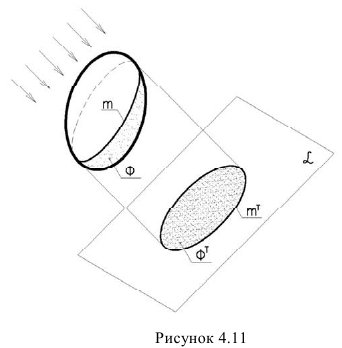
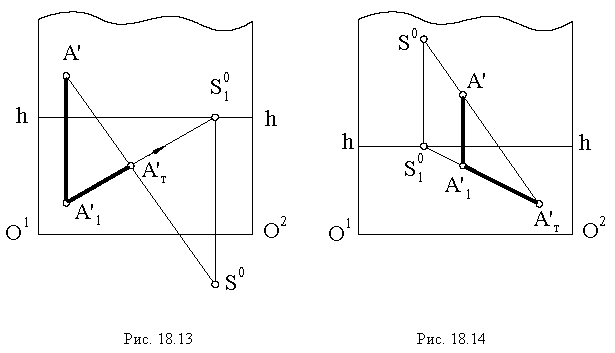
Для поверхностей характерны следующие понятия: Собственная тень (ф) – неосвещенна часть поверхности (предмета) рисунок 4.11.
Контур собственной тени (ш)-граница между освещенной и неосвещенной частью поверхности (предмета).
Падающая тень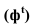
Контур падающей тени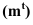
Фактически контур падающей тени -это тень от контура собственной тени. Поэтому, обычно, сначала определяют контур собственной тени, а затем уже строят падающую.
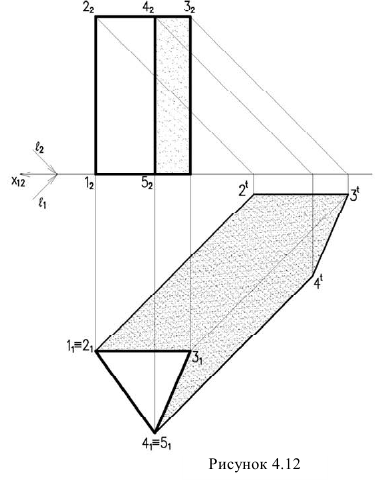
Рассмотрим примеры построения теней трехгранной призмы (рисунок 4.12) и прямого кругового конуса (рисунок 4.13).
Проведя лучи на горизонтальной проекции касательные к крайним ребрам призмы, определяем контур собственной тени. Она является пространственной ломаной 1,2,3,4,5. Т.к. точки 1 и 5 лежат на плоскости 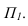
Поэтому для построения контура падающей тени, достаточно построить тени точек 2,3,4.
Проанализировав построенную тень, мы видим, что тени от ребер 1,2 и 5,4 совпадают с направлением лучей, т.к. они перпендикулярны к плоскости 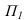
Учитывая это, построение контуров падающих теней многогранников может быть значительно упрощено.
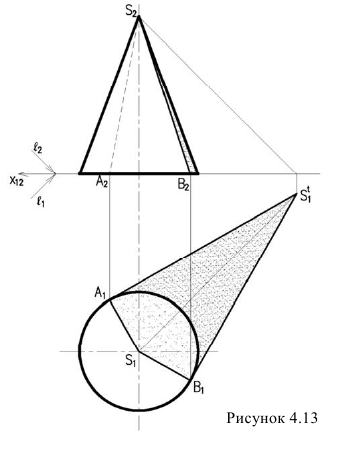
Для конуса логично сначала построить падающую тень, а затем собственную (рисунок 4.13). Для построения падающей тени, строим тень от вершины конуса
Из полученной точки проводим касательные к окружности основания. Эти касательные образуют, контур падающей тени (она является тенями от образующих конуса). Поэтому, соединив точки А и В с вершиной конуса S получим границы собственной тени конуса. А затем уже строим фронтальную проекцию контура собственной тени. Аналогично строятся тени пирамидальных поверхностей.
Тени в ортогональных проекциях. Метод лучевых сечений, метод обратных лучей. Тени фрагментов зданий
Тень точки и прямой на плоскость общего положения (способ лучевых сечений, способ обратных лучей).
Тени схематизированного здания, состоящего из призматических форм.
Тени фрагментов зданий.
Тень точки на плоскость общего положения. Способ лучевых сечений
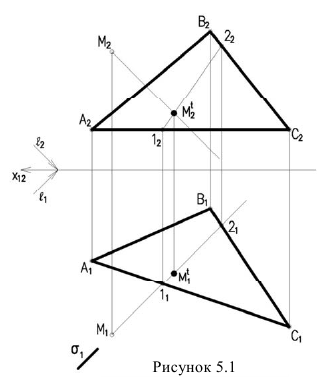
Для построения тени точки М на плоскость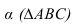
Через луч проводим горизонтально-проецирующую лучевую плоскость о. Строим линию пересечения 1-2 плоскости а и заданной плоскости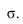
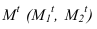
Способ обратного луча
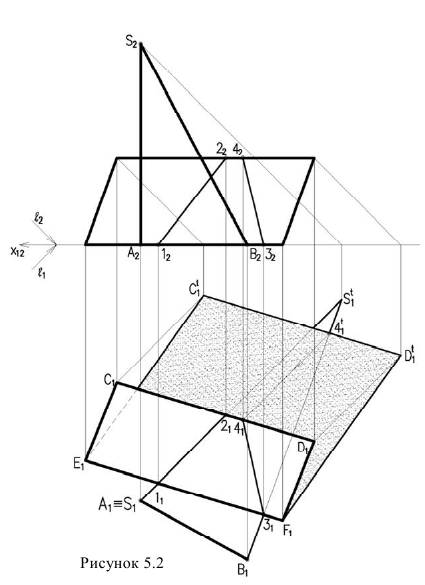
Рассмотрим построение тени от двух прямых SF и SB на непрозрачную пластинку ECDF. (рисунок 5.2).
Тень от проецирующей прямой SA строится, аналогично предыдущему примеру (рисунок 5.1), методом лучевых сечений. На горизонтальной проекции тень совпадает с направлением луча, на фронтальной – идет по лучевому сечению. Тень от точки S на пластину ESDF не надает. Для построения тени от наклонной прямой SB на пластину ESDF, необходимо построить сначала тень падающую на плоскость 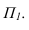
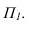
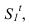
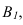
Далее строим тень от пластины ESDF на плоскость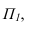
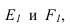
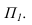
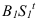
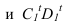
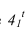
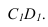
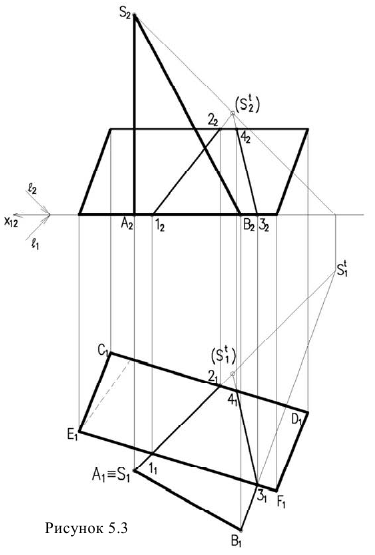
Необходимо отметить что данную задачу можно решить используя построение мнимой тени от точки S на пластину ESDF (рисунок 5.3).
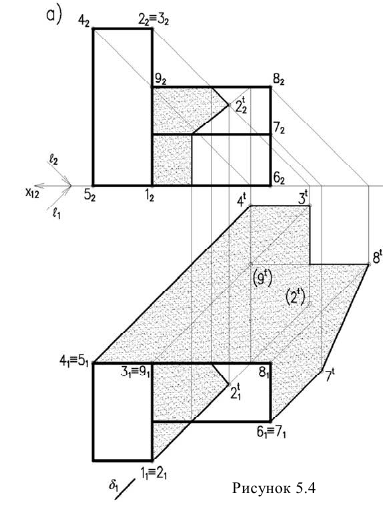
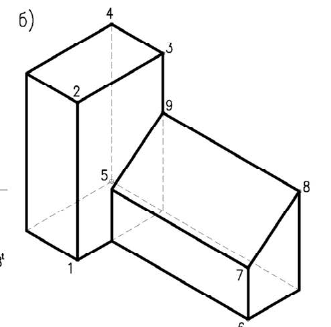
Тени схематизированною здании, состоящею из призматических форм
Здание состоит из двух призматических форм (рисунок 5.4). Обычно сначала строятся тени от двух этих форм падающие на плоскость 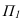
Дли построении падающих теней определяем контур собственной тени каждой из призм (рисунок 5.46). Высотная часть здания представляет прямую призму, контур собственной тени которой 1,2,3,4,5, причем точки 1 и 5 лежат на плоскости, поэтому тени строим от трех точек 2,3,4. Контур собственной тени второй призмы – 6,7,8,9. Точка 6 лежит на 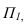
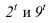
Для построения тени падающей от высотной части здания на пристройку используем метод лучевых сечений. Заключаем луч, проведенный через точку 2 в плоскость 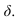
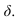
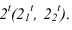
При построении теней зданий очень важно помнить положение теней прямых частного положения, это значительно упрощает процесс построения.
Тени фрагментов зданий
К фрагментам зданий относятся ниши, козырьки, трубы, лестницы и т.п. Рассмотрим построение теней некоторых из них.
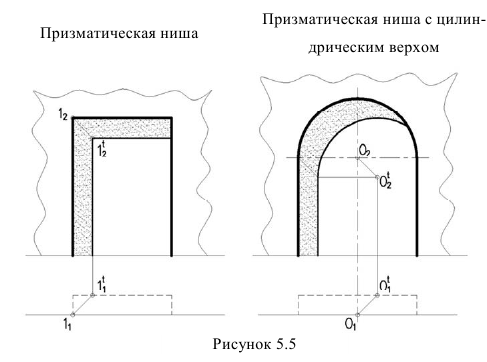
Тени в нишах
Две изображенные ниши относятся к нишам с плоским днищем, т.е. контур ниши отбрасывает тень на плоскость днища ниши параллельной контуру. Поэтому тени в нишах с – плоским днищем повторяют контур ниши. Для построения таких теней достаточно построить тень одной точки, как показано на примере (рисунок 5.5). Если дан лишь фасад здания, необходимо знать глубину ниши и тень построить методом выноса.
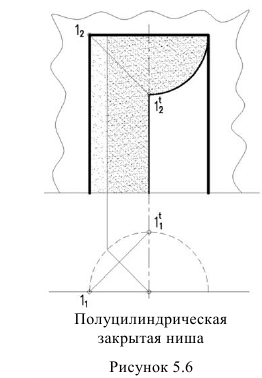
В цилиндрической нише (рисунок 5.6) сначала определяем собственную тень. Для чего удобнее провести нормаль (т.е. радиус под углом 45°). Получим контурную образующую собственной тени.
Падающую тень будет отбрасывать две прямые кромки ниши – вертикальная и продольная. Тень от вертикальной прямой надает на ось ниши. Тень от продольной прямой будет представлять четверть окружности.
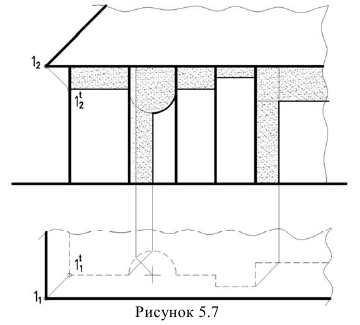
Из этого чертежа можно сделать вывод: тень от продольной прямой на фасаде с вертикальными образующими зеркально повторяется план. Этот вывод позволяет построить тень на фасаде от свеса крыши, построив тень одной точки (тень точки 1 на рисунке 5.7). Остальной контур тени зеркально повторяет план.
Тень падающая от трубы на крышу
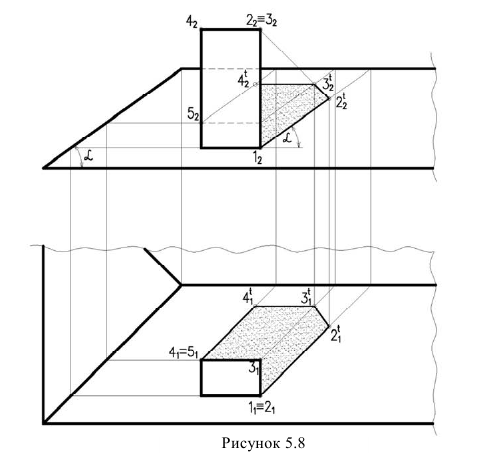
На рисунке 5.8 дана труба призматической формы.
Тень строится методом лучевых сечений. Если отсутствует план здания, то нужно иметь ввиду, что тени от вертикальных прямых на фасаде имеют угол наклона равный углу наклона ската крыши
Тень от барьера на ступенях лестницы
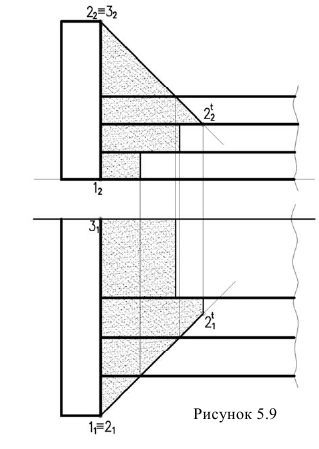
Контур собственной тени барьера (рисунок 5.9), отбрасывающий тень на ступени представляет собой две прямые – горизонтально-проецирующую 1,2 и фронтально-проецирующую 2,3. Из точек 1 и 3 начинается тень. Следовательно, необходимо построить тень точки 2. Для построения падающей тени используется метод лучевых секущих плоскостей.
Тени в ортогональных проекциях
Строительство зданий и сооружений ведется по чертежам, выполненным в ортогональных проекциях. Представление о внешнем виде здания, в основном, создается по изображению фасада. Это изображение имеет существенный недостаток – в нем отсутствует объемность. Тени, построенные на ортогональных чертежах, дают возможность представить по чертежу расположение отдельных элементов, их освещенность, а также помогают находить наилучшие пропорции проектируемых зданий и сооружений.
При освещении лучами света каких-либо объектов на них образуются тени. Для образования тени необходим источник света и плоскость, на которую падает тень.
Освещение может быть центральным (факельным) или параллельным (солнечным). Освещение называется центральным в случае, когда световые лучи идут из одной точки (лампа, свеча); параллельным, если источник света (солнце) удален в бесконечность, и световые лучи практически будут параллельны между собой.
Основной геометрической задачей построения теней является определение контуров собственных и падающих теней (рис. 17.1).
Неосвещенная часть поверхности тела 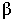
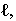
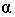
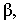
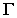
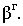
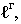
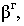
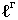
Для построения падающей тени необходимо знать направление лучей света. Направление световых лучей 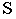
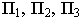
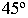
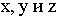
Тень от точки на плоскость проекций
Тенью от точки 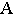
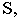
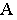
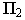
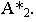
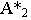
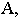
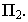
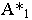
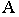
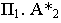
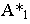
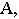
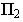
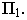
Тень от точки на плоскую фигуру
Чтобы построить тень от точки на плоскость общего положения (рис. 17.5), необходимо найти точку пересечения луча света, проходящего через заданную точку 
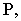
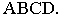
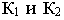
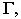
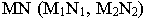
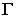
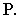
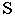
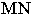
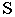
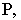
- Заказать чертежи
Тень от прямой линии
Построение тени от отрезка прямой линии сводится к определению тени двух или нескольких его точек. Тень от прямой можно рассматривать как след лучевой плоскости, проходящей через данную прямую. В зависимости от положения прямой, лучевая плоскость может быть общего и частного положения. Линия пересечения её с плоскостями или поверхностями определит форму тени от отрезка прямой.
Тени на плоскости проекций от прямые частного положения
Построение тени от отрезка прямой 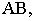
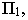
Тень 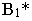
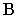
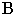
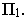
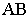
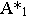
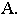
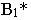
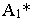
Вывод. Тень от прямой, перпендикулярной плоскости проекций, совпадает с проекцией светового луча на эту плоскость.
На рис. 17.7 показано построение тени от отрезка прямой 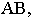
Вывод. Тень от отрезка прямой, параллельной плоскости проекций, на этой плоскости равна и параллельна самому отрезку.
Тени на плоскости проекций от прямых общего положения
На рис. 17.8 показано построение тени от отрезка прямой 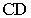
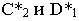
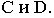
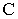
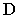
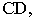
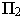
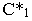
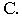
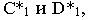
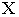
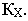
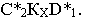
Тень от прямой на произвольную плоскость
Для построения тени от прямой на плоскость общего положения достаточно определить тени на эту плоскость от двух любых точек прямой (см. построение тени от точки на плоскую фигуру, рис. 17.5).
Тень от плоской фигуры
Падающая тень от плоской фигуры на плоскости проекций может быть построена как совокупность теней от её вершин и сторон. Таким образом, построение тени от плоской фигуры на плоскость проекций может быть сведено к известному определению теней от точек и прямых.
На рис. 17.9 показано построение тени от треугольника 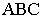
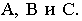
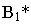
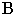
На рис. 17.10 построена тень от круглой пластины, перпендикулярной плоскости проекций 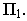
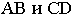
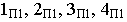
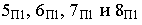
Соединив полученные точки, получим контур падающей тени круглой пластины, перпендикулярной плоскости
Метод обратных лучей
Метод обратных лучей применяется при построении теней, падающих от одного предмета на другой. Суть метода заключается в том, что строят тени заданных геометрических фигур на одну из плоскостей проекций и определяют точки пересечения теней. Через отмеченные точки проводят луч, направление которого противоположно световым лучам. Каждый из обратных лучей, пересекая данные геометрические фигуры, определяет нужные для построения тени точки.
На рис. 17.11 показано применение этого метода на примере построения тени прямой на плоскость треугольника. Построены падающие тени треугольника 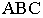
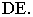
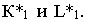
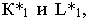
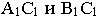
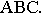
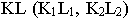
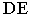
Вывод. Если падающие тени двух геометрических образов пересекаются, то тень от одного из них будет падать на другой
Тени геометрических тел
При построении теней геометрических тел вначале определяют контур собственной тени, затем находят контур падающей тени путем построения падающих теней от вершин и сторон ломаной линии (или точек кривой линии), являющейся контуром собственной падающей тени
В отдельных случаях бывает целесообразно определять контур собственной тени по уже построенной падающей тени.
Рассмотрим процесс построения теней от основных геометрических тел.
Тени призмы
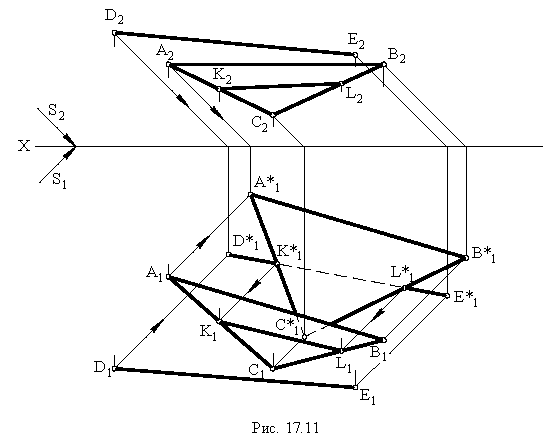
Контур тени от призмы определяется тенями от рёбер (рис. 18.1). Освещенность призмы легко определить по горизонтальной проекции, где видно, что обращенными к свету являются две грани 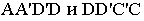
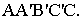
Тени пирамиды
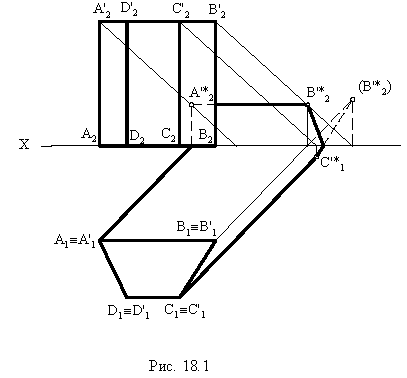
Построим тени пятиугольной пирамиды (рис. 18.2). Строим падающую тень 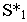
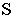
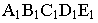
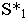
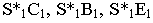
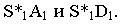
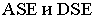
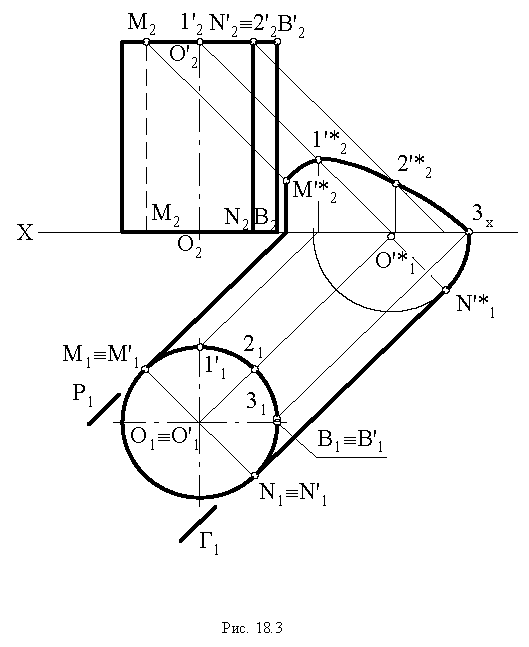
Тени цилиндра
Для определения контура собственной тени прямого кругового цилиндра необходимо провести две горизонтально-проецирующие лучевые плоскости 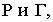
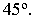
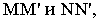
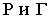
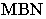
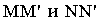
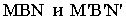
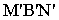
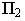
Тени конуса
На рнс. 18.4 показано построение собственной и падающей теней прямого кругового конуса. Вначале определяем мнимую тень от вершины конуса 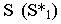
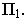
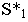
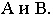
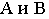
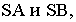
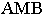
Тени элементов зданий
При построении проекций теней на фасадах зданий используются те же приемы, что и при построении теней геометрических тел.
Рассмотрим примеры построения теней некоторых частей здания
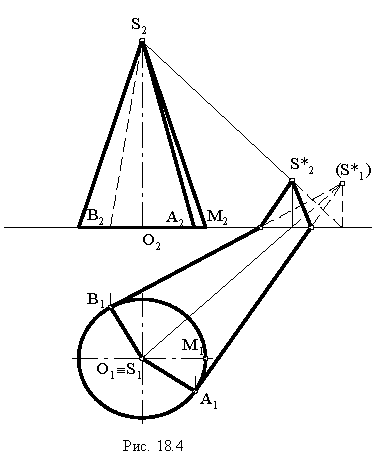
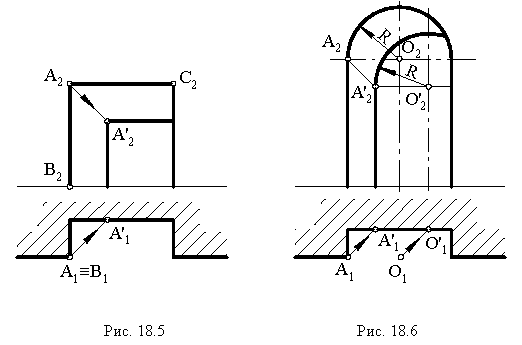
На рис. 18.5 показан пример построения теней в плоской нише. Определение границы падающей тени заключается в построении тени от ломаной линии 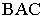
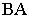
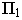
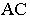
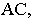
На рис. 18.6 приведен пример построения тени в прямоугольной нише с цилиндрической аркой В этом примере надо найти тень от точки 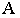
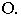
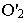
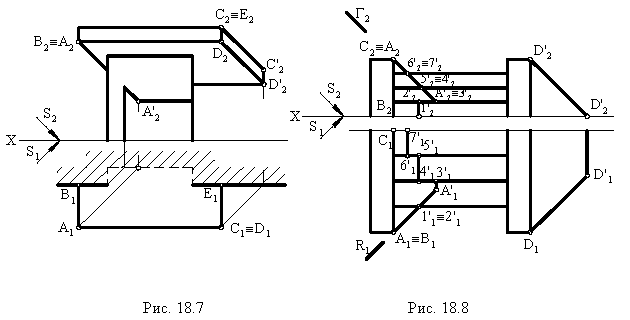
На рис. 18.7 построена тень от козырька (или балкона) здания Построения понятны из чертежа.
На рис. 18.8 показано построение теней на лестнице (крыльце). В собственной тени находятся правые грани вертикальных стенок. Падающая тень от правой стенки лестницы на плоскость стены здания и на землю строится как тень от плоской фигуры на плоскости проекций 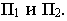
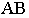
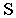
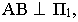
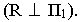
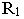
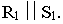
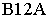
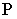
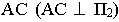
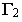
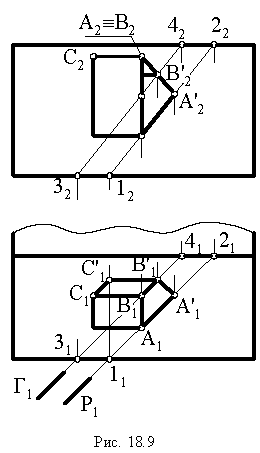
На рис. 1S.9 показано построение контура падающей тени от трубы на скат крыши здания Задача сводится к определению теней от точек и прямых на произвольно расположенную плоскость (скат крыши). Построения выполнены способом вспомогательных секущих лучевых плоскостей 
Тени в перспективе
При построении теней в перспективе в качестве источника света рассматривается естественный источник – солнце. Правила построения теней в перспективе точно такие же, как и в ортогональных проекциях.
Для упрощения построения считают, что световые лучи параллельны плоскости картины, тогда на картине перспективы оснований лучей будут параллельны основанию картины
Если на картине задана перспектива 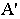
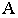
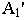
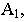
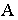
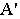
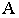
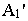
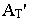
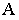
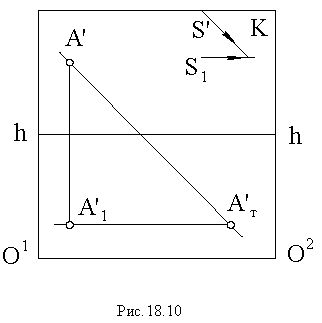
Построение тени от прямой сводится к построению тени от двух ее точек. При этом, если прямая перпендикулярна предметной плоскости (рис. 18.11), то тень от нее на этой плоскости совпадает с основанием луча, проведенного через основание прямой.
Тень от вертикальной прямой на вертикальной плоскости вертикальна.
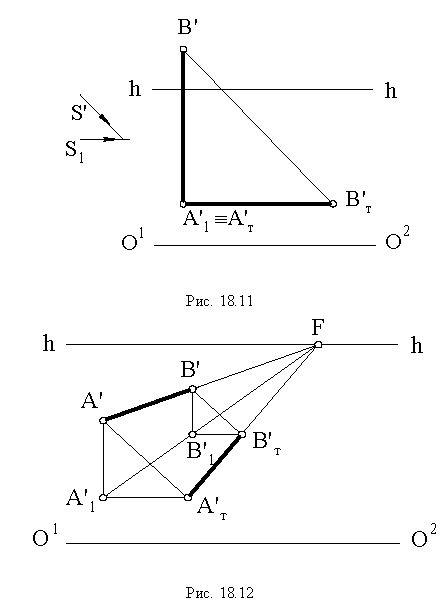
Если прямая параллельна предметной плоскости (горизонтальная прямая), то тень от нее на этой плоскости будет параллельна данной прямой (рис. 18.12) и направлена в точку схода.
Тени в перспективе могут быть построены с различных точек расположения источника света. Направление лучей света может быть выбрано в зависимости от характера объекта и от желания показать его освещенным с той или другой стороны. Так, например, если источник света будет находиться позади предмета (рис. 18.13) или перед зрителем, но позади предмета (рис. 18.14), то для построения перспективы тени 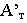
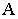
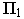
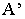
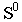
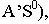
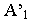
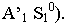
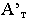
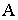
- Кривые поверхности
- Пересечения криволинейных поверхностей
- Пересечения поверхностей с прямой и плоскостью
- Взаимное пересечение поверхностей
- Развертки поверхностей
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
- Решение метрических задач
-
Построение теней
План:
7.1. Основы теории теней
7.2. Тени от точки, линии и плоской фигуры
7.3. Тень, падающая от одной фигуры на
другую
7.4. Тени геометрических тел
7.5. Тени пересекающихся многогранников
(от здания)
7.6. Тени на фасадах зданий
-
Основы теории теней
Нанесением теней
пользуются для придания проекционным
чертежам большей наглядности. Особенно
широко используются тени при оформлении
архитектурных проектов, а также для
решения ряда практических задач
(например, для выявления освещенности
наружных или внутренних частей сооружения
при определенных условиях, для определения
размеров сооружения по отбрасываемой
им тени и т.п.).
Различают
собственные и падающие тени.
СОБСТВЕННОЙ
называется тень, которая получается
на неосвещенной поверхности предмета
(или объекта) при освещении его каким-либо
источником света (рис. 72).
Рис.
72
ПАДАЮЩЕЙ
называется тень, отбрасываемая
предметом на плоскости проекций, или
возникающая на поверхности предмета
из-за того, что на пути лучей света
расположен другой предмет.
Если предмет
освещается источником света, находящимся
на конечном расстоянии от него (факелом,
лампой, свечой), то совокупность световых
лучей, падающих на предмет, образует
конус или пирамиду. Такая тень называется
ФАКЕЛЬНОЙ.
Если же источник
света находится в бесконечности, то
совокупность световых лучей образует
цилиндр или призму. Тень при этих
условиях называется СОЛНЕЧНОЙ.
НАПРАВЛЕНИЕ
СВЕТОВЫХ ЛУЧЕЙ. При построении теней
в ортогональных проекциях, направление
lлучей света обычно принимают
параллельным диагонали куба, грани
которого параллельны плоскостям
проекций (рис. 73).
Рис.
73
Диагональ куба
АВобразует с плоскостями проекций
углы, равные 35о16′, а проекции ее
наклонены к плоскостям H, V, и W под углом
45o.
При построении
теней в аксонометрии, направление лучей
света, параллельное диагонали куба, не
всегда дает удачное расположение
светотеней; в таких случаях следует
выбрать другое направление, обеспечивающее
выразительность чертежа.
-
Тени от точки, линии и плоской фигуры
ПАДАЮЩАЯ ТЕНЬ ОТ
ТОЧКИ
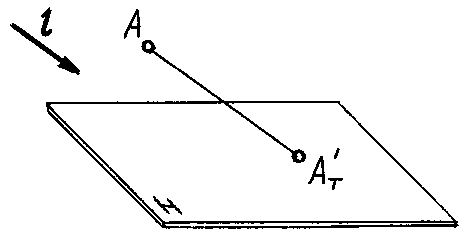
Представим себе
материальную точку А(рис. 74),
расположенную в пространстве над
плоскостью Н, которая освещается
световыми лучами, идущими из бесконечности
параллельно заданному направлениюl.
ТочкаАзадержит один из них и
отбросит теневой луч, который пересечет
плоскость Н в точкеАТ‘. Эта
точка и будет являться тенью точкиА.
Иными словами,
тень точки является следом теневого
луча.
Итак, чтобы
построить тень, падающую от точки на
какую-либо плоскость или поверхность,
необходимо через данную точку провести
прямую, параллельную направлению лучей
света, и определить точку пересечения
этой прямой с плоскостью или поверхностью,
на которую падает тень.
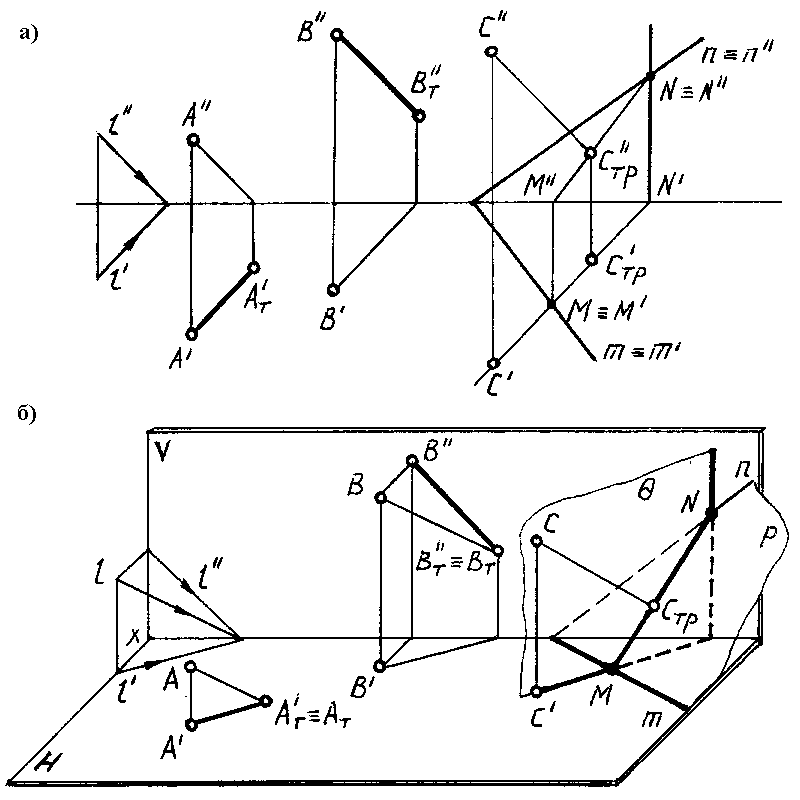
На рис. 75а в
ортогональных проекциях и на рис. 75б
в аксонометрии построены тени, падающие
на плоскости Н, V и P(nm) от точекА,ВиС.
Рис.
74
Рис.
75
Тень от точки
Ападает на плоскость Н в точкеАТ‘ (эта точка является
горизонтальным следом лучаААТ).
Тень от точки Впадает на плоскость V в точкеBТ”
(эта точка является фронтальным
следом лучаАВТ).
Тень от точки в
аксонометрииопределяется в результате
пересечения луча с его вторичной
проекцией.
Тень ВT”
(в аксонометрии) можно построить как
точку пересечения лучаВВТ с
его фронтальной проекциейВ”BT”или при помощи горизонтальной проекции
луча.
Тень от точки
Спадает на плоскость P (nm) в точкеСTP (СTP‘, СTP”),
которая определяется в результате
пересечения лучаССT с заданной
плоскостью Р при помощи
горизонтально-проецирующей плоскости.
ПАДАЮЩАЯ ТЕНЬ ОТ
ПРЯМОЙ ЛИНИИ
Тень, падающая от
прямой линии, состоит из падающих теней
от всех ее точек. Лучи, проходящие через
все точки прямой, образуют лучевую
плоскость, а тень от прямой линии есть
линия пересечения лучевой плоскости
с плоскостью или поверхностью, на
которую падает тень (то есть след лучевой
плоскости).
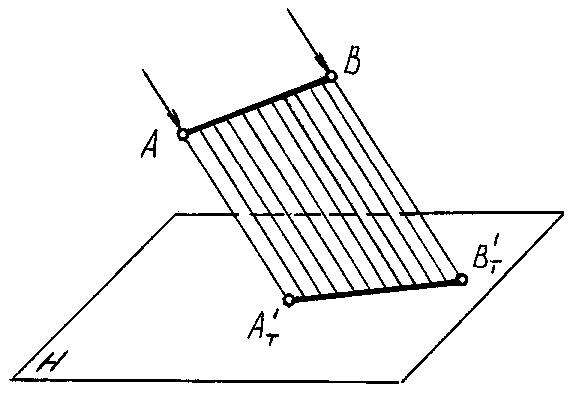
Тенью, падающей
от прямой на плоскость, является прямая
линия, поэтому для ее построения
достаточно построить тени от двух
точек, принадлежащих этой прямой
(рис. 76).
Рис.
76
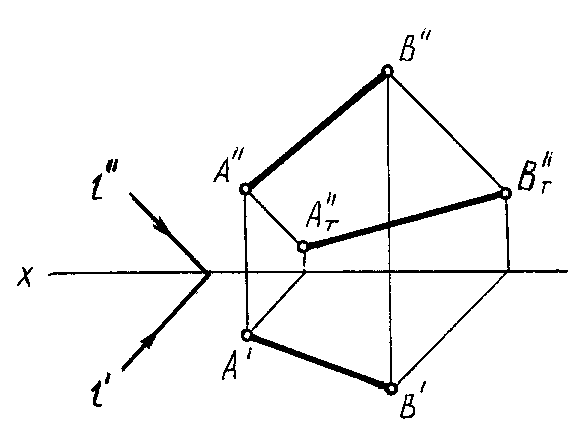
На рис. 77
построена тень на плоскости проекций
от отрезка АВ на комплексном чертеже.
Рис.
77
Тени от точек А
и B
в этом
примере падают на одну плоскость
проекций V, поэтому для построения тени
отрезкаАВдостаточно соединить
между собой полученные точкиАT”
иВT” прямой линией.
ПРИМЕР.
Построить падающую тень на H и V от
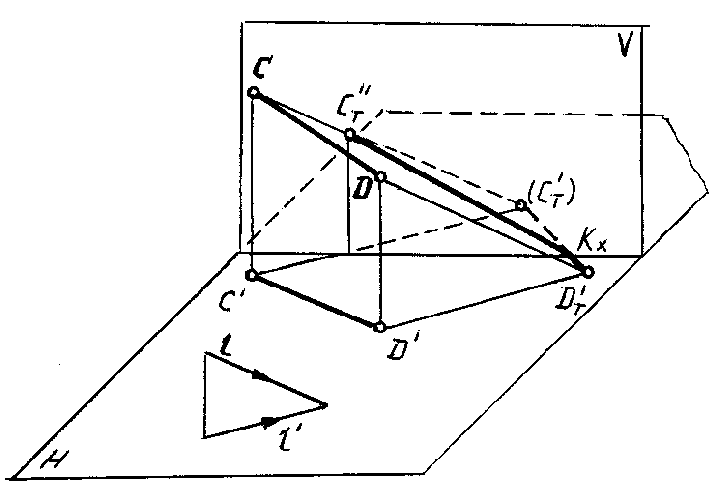
отрезка прямойСD(рис. 78, 79).
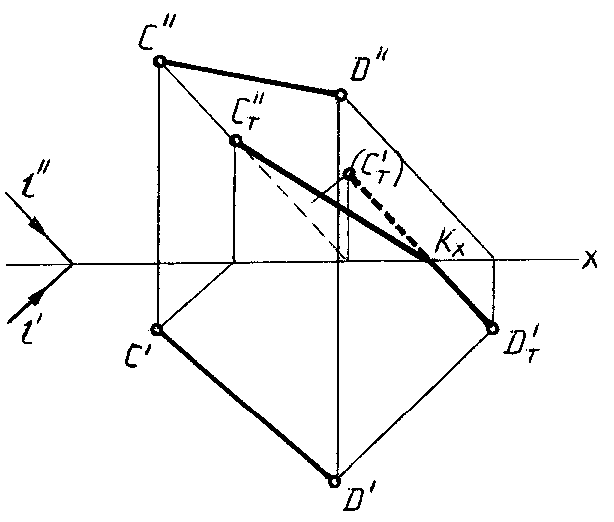
Рис. 78 Рис.
79
Решение. Тень от
отрезка СDпадает на две плоскости
проекций и представляет собой ломаную
линиюCT”KXDT‘.
Точку переломаКX можно
определить двумя способами:
1) при помощи
мнимой тени(рис. 78, 79).
Для этого строят
тень отрезка на одну из плоскостей
проекций, предполагая, что второй не
существует. На рисунке сначала построена
тень отрезка на плоскость Н (СT‘DT‘).
Построенная тень пересекает осьОХв точкеКX, в этой точке тень
переломится и с одной плоскости перейдет
на другую (в точкуСT”).
2) при помощи
тени от промежуточной точки(рис.
80).
Рис.
80
На чертеже точка
перелома КX определяется при
помощи тени от произвольной промежуточной
точкиЕ (ЕT”).
Тени от прямых,
находящихся в частных положениях
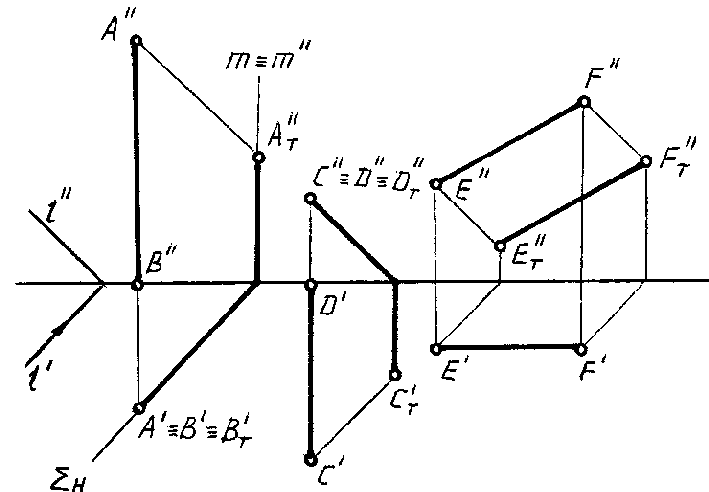
ПРИМЕР. В
ортогональных проекциях заданы отрезки
частного положенияАВ,СDиEF.
Построить тени, падающие от этих отрезков
на плоскости проекций H и V (рис. 81).
Рис.
81
Решение.
1. Отрезок АВ
занимает вертикальное положение,
поэтому лучи, проходящие через все его
точки, образуют вертикальную
(горизонтально-проецирующую) лучевую
плоскость , которая
пересечет плоскость Н по линииH,
а плоскость V — по вертикальной
прямойm=m”. Следовательно,
тень от вертикальной прямой линии на
горизонтальной плоскости совпадает с
горизонтальной проекцией (следом)
лучевой плоскости.
Но, так как
горизонтальная проекция лучевой
плоскости параллельна горизонтальной
проекции луча света, то для построения
тени на горизонтальной плоскости
проекций (от вертикальной прямой)
достаточно через горизонтальную
проекцию прямой (точку) провести
горизонтальную проекцию луча света.
2. Отрезок CDперпендикулярен плоскости V, поэтому
проходящая через него лучевая плоскость
является фронтально-проецирующей
плоскостью.
В ортогональных
проекциях тень от прямой СDна
плоскости V совпадает с проекцией
лучевой плоскости.
3. Отрезок EFпараллелен плоскости V. Его теньET”FT”
параллельна и равна данному отрезку.
В ЫВОДЫ:
1. Тень от
прямой, перпендикулярной к плоскости,
совпадает с ортогональной проекцией
светового луча на эту плоскость.
2. Тень, падающая
на плоскость от отрезка прямой,
параллельной этой плоскости, параллельна
и равна отрезку прямой. На комплексном
чертеже проекция тени равна и параллельна
проекции отрезка.
ТЕНЬ ОТ ПЛОСКОЙ
ФИГУРЫ
(непрозрачной
пластинки)
Чтобы построить
падающую тень от плоской фигуры,
ограниченной многоугольником, достаточно
построить тени, падающие от всех сторон
многоугольника.
На рисунке 82
построена тень, падающая от треугольника
АВСна плоскости проекций H и V.
Тень от вершиныАпадает на плоскость
V, а от вершиныВи вершиныС— на
плоскость Н. Следовательно, тень от
стороныВСпадает на одну плоскость
Н и представляет прямую линию, а тени
от сторонАВиАСпадают на две
плоскости и представляют ломаные линии.
Рис.
82
Падающие тени от
сторон АВиАСможно построить
при помощи промежуточных точек (как на
чертеже 81) или при помощи мнимой тени
(АT‘), падающей от точкиАна заднюю полуплоскость Н. Получив
треугольникАTHВTHСTH,
определяем на осиОХточки перелома
1 и 2 падающей тени и соединяем их
с действительной теньюАTV от
точкиАна плоскости V. Сторона
плоской фигуры, обращенная к теневому
столбу, находится в тени, то есть у
плоских фигур следует различать
освещенную и неосвещенную стороны.
Иначе говоря, плоская фигура всегда
имеет собственную тень.
Для выяснения
освещенности сторон плоскости
треугольника применяем следующий
прием: обходя на исследуемой проекции
периметр треугольника по часовой
стрелке, замечаем порядок букв,
обозначающих вершины, и сопоставляем
с порядком букв, который получается
при обходе по часовой стрелке контура
падающей тени. Совпадение порядка букв
обозначает, что на данной проекции
видима освещенная сторона треугольника,
несовпадение — что видима
неосвещенная сторона плоскости.
На рисунке контур
падающей тени при его обходе по часовой
стрелке дает порядок букв АT”СT”ВT”.
Такой же порядок (А”є”)
получается на фронтальной проекции.
Следовательно, на V видима освещенная
сторона. Горизонтальная проекция имеет
обратный порядок букв (А‘‘ё).
Это значит, что на горизонтальной
проекции к нам обращена неосвещенная
сторона плоскости треугольника (сторона,
находящаяся в собственной тени).
Этим же приемом
можно пользоваться в аксонометрии
(рис. 83).
Рис.
83
ТЕНЬ ОТ ДИСКА
(окружности)
Если плоская
фигура, бросающая тень, ограничена
кривой линией, то лучи, проходящие через
точки этой кривой, образуют цилиндрическую
лучевую поверхность. В пересечении с
плоскостью, на которую падает тень, эта
поверхность дает контур падающей тени
данной фигуры.
Если плоскость
фигуры параллельна плоскости, на которую
падает тень, то тень равна самой фигуре
(так как равны параллельные между собой
основания цилиндра).
На рис. 84 показано
построение тени от круга, параллельного
плоскости H, на плоскость H. Контуром
тени является окружность тог же радиуса.
Для построения тени достаточно найти
тень от центра С.
Рис.
84
Для построения
тени, падающей от кривой линии на
произвольно расположенную плоскость,
можно применить один из двух способов.
1. На кривой
линии намечается достаточно большое
число точек, от которых строится падающая
тень. Полученные точки (падающей тени)
соединяются между собой плавной кривой
линией.
2. Около кривой
линии описывается многоугольник,
строится падающая тень от многоугольника
и в нее вписывается тень кривой линии.
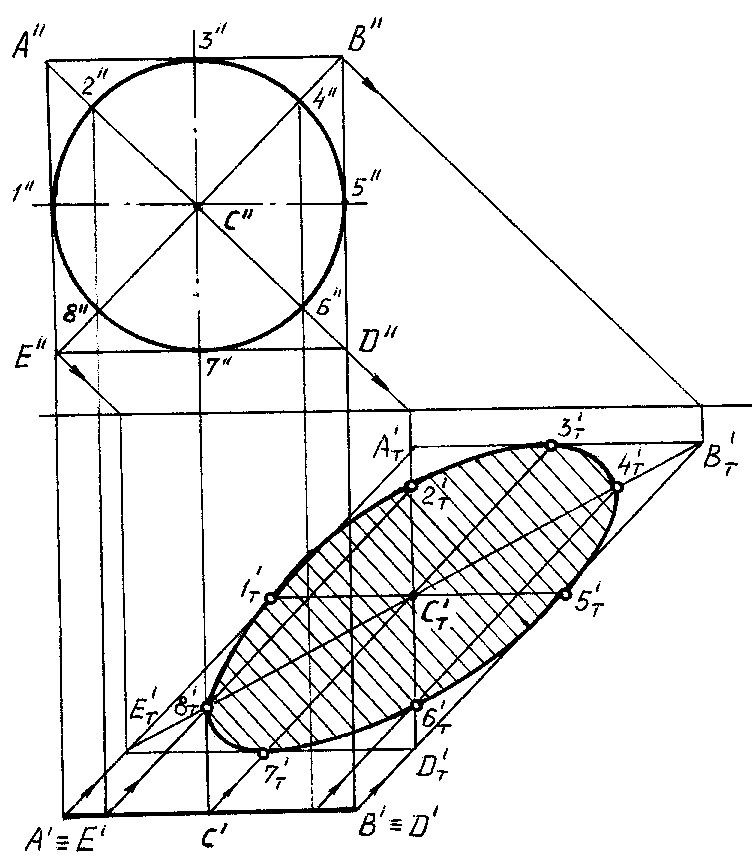
На рис. 85 для
построения падающей тени от круга,
параллельного плоскости V, на плоскость
Н использован описанный около него
квадрат АBCD. Сначала строится
падающая тень от сторон квадрата, его
диагоналей и линий, проходящих через
центрСпараллельно сторонам
квадрата, а затем вписывается в полученный
параллелограмм кривая (эллипс). На
рисунке эллипс проходит через восемь
точек, принадлежащих одновременно
падающим теням от окружности, сторон
и диагоналей квадрата.
Если тень от кривой
линии падает на две пересекающиеся
плоскости, то она будет иметь излом на
линии пересечения плоскостей.
Рис.
85
Слайд 1Тени в ортогональных проекциях

Слайд 2
Леонардо Да Винчи (Leonardo Da Vinci) (1452-1519)
Рельефность
«происходит от теней и светов или, другими
словами, от светлого и темного.
Итак, кто избегает теней, избегает славы искусства»
ТЕНИ

Слайд 3Форма предмета воспринимается точнее, когда предмет освещен
и на его поверхности образуется светотень
Характер светотени
зависит от положения предмета относительно источника света
и направления лучей к поверхности
Изображение светотени на проекционных чертежах состоит из двух графических операций:
«геометрия теней»;
«изображение светотени» («отмывка»)

Слайд 4«геометрия теней» – это определение границ (контуров)
собственных и падающих теней, основанное на построении
линии прикосновения лучевой поверхности с данной поверхностью и определение линии пересечения поверхностей
«изображение светотени» («отмывка»)- графические приемы выявления светотени на изображении так, чтобы ее восприятие наиболее близко подходило к восприятию в натуре. Эта операция основана на физиологии зрительного восприятия, т.е. на «воздушной перспективе»

Слайд 5Чем освещенное место ближе к зрителю, тем
оно кажется светлее и ярче, а чем
дальше – тем бледнее и мягче
Светотеневой контраст (различие между освещенной и теневой частью предмета) по мере удаления от зрителя погашается, делается менее резким
ВОЗДУШНАЯ ПЕРСПЕКТИВА

Слайд 6
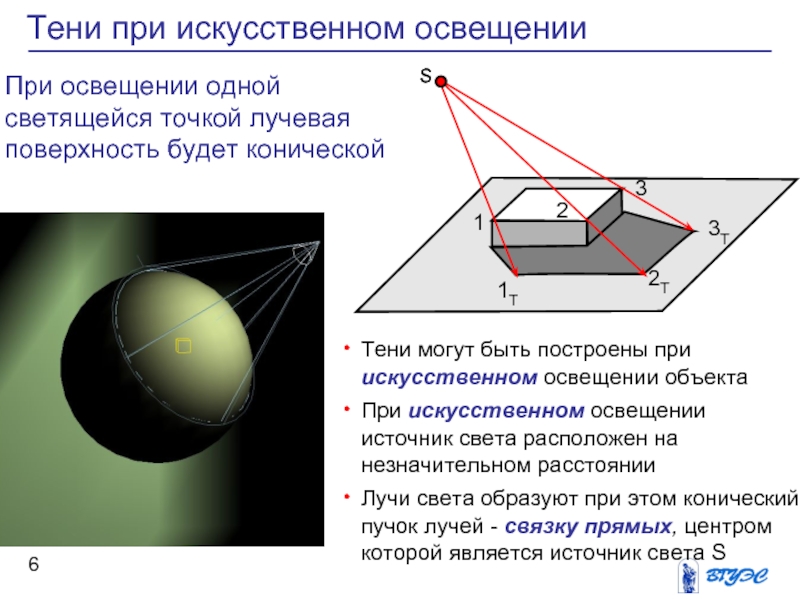
Тени могут быть построены при искусственном освещении
объекта
При искусственном освещении источник света расположен на
незначительном расстоянии
Лучи света образуют при этом конический пучок лучей – связку прямых, центром которой является источник света S
Тени при искусственном освещении
s
1
2
3
3Т
2Т
1Т
При освещении одной светящейся точкой лучевая поверхность будет конической
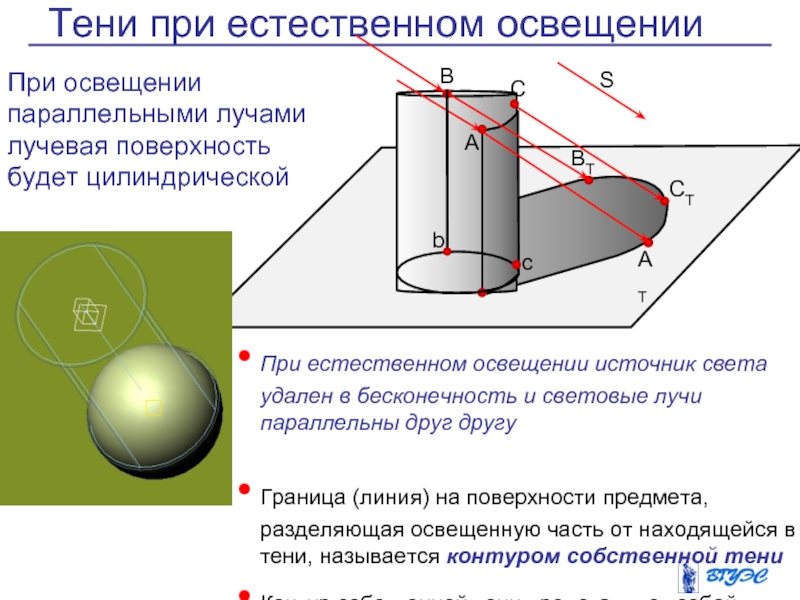
Слайд 7Тени при естественном освещении
При освещении параллельными лучами
лучевая поверхность будет цилиндрической
В
A
C
CT
S
AT
BT
b
c
При естественном освещении источник
света удален в бесконечность и световые лучи параллельны друг другу
Граница (линия) на поверхности предмета, разделяющая освещенную часть от находящейся в тени, называется контуром собственной тени
Контур собственной тени представляет собой линию касания обертывающей лучевой поверхности к поверхности предмета
Слайд 8Падающие тени
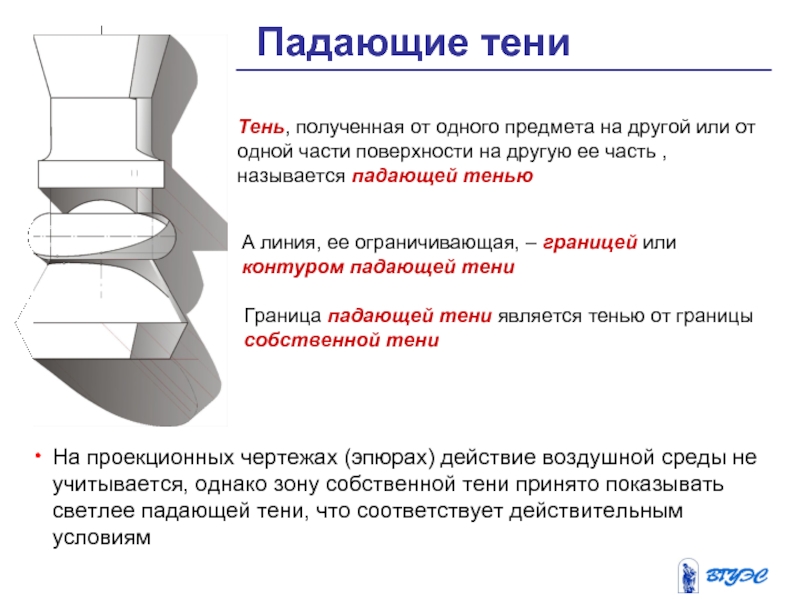
Тень, полученная от одного предмета на
другой или от одной части поверхности на
другую ее часть , называется падающей тенью
А линия, ее ограничивающая, – границей или контуром падающей тени
Граница падающей тени является тенью от границы собственной тени
На проекционных чертежах (эпюрах) действие воздушной среды не учитывается, однако зону собственной тени принято показывать светлее падающей тени, что соответствует действительным условиям
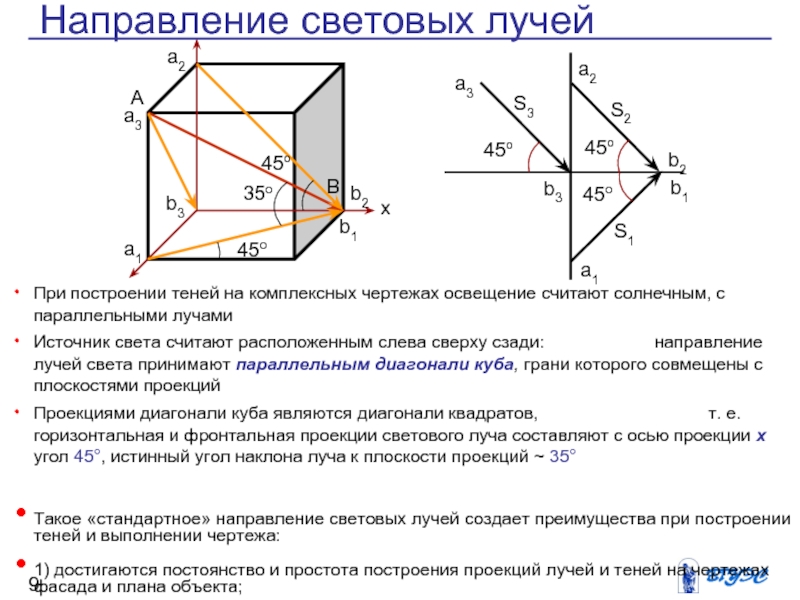
Слайд 9При построении теней на комплексных чертежах освещение
считают солнечным, с параллельными лучами
Источник света считают
расположенным слева сверху сзади: направление лучей света принимают параллельным диагонали куба, грани которого совмещены с плоскостями проекций
Проекциями диагонали куба являются диагонали квадратов, т. е. горизонтальная и фронтальная проекции светового луча составляют с осью проекции х угол 45°, истинный угол наклона луча к плоскости проекций ~ 35°
Такое «стандартное» направление световых лучей создает преимущества при построении теней и выполнении чертежа:
1) достигаются постоянство и простота построения проекций лучей и теней на чертежах фасада и плана объекта;
2) облегчаются чтение чертежа и понимание форм, пропорций и размеров элементов изображенного объекта.
Направление световых лучей
35о
45о
45о
x
A
B
a2
a3
b2
a1
b1
b3
b3
a3
a2
b2
a1
b1
45о
45о
45о
S3
S2
S1
Слайд 10
35о
45о
45о
z
x
y
A
B
a2
a3
b2
a1
b1
b3
b3
a3
a2
b2
a1
b1
45о
45о
45о
S3
S2
S1
35о
1
2
3
4
5
45о
45о
0,7(0,707)
0,3(0,293)
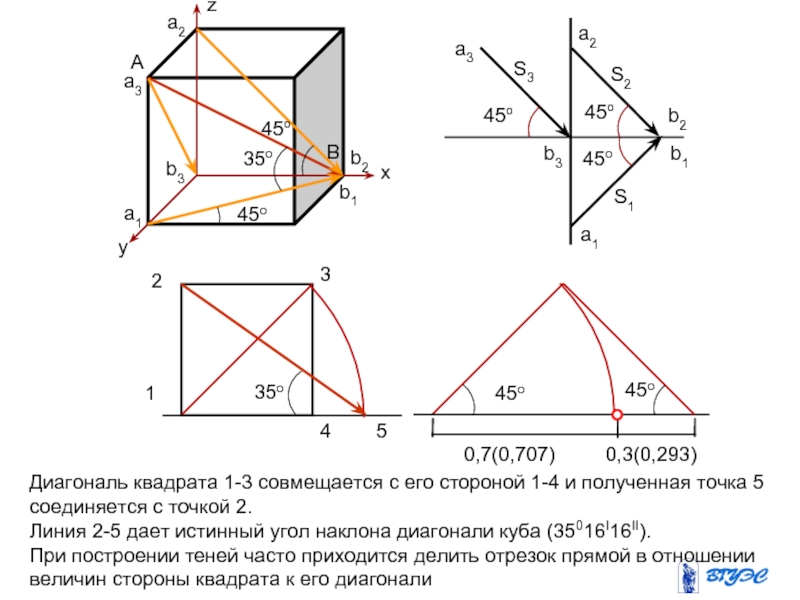
Диагональ квадрата 1-3 совмещается с его стороной
1-4 и полученная точка 5 соединяется с
точкой 2.
Линия 2-5 дает истинный угол наклона диагонали куба (35016I16II).
При построении теней часто приходится делить отрезок прямой в отношении величин стороны квадрата к его диагонали
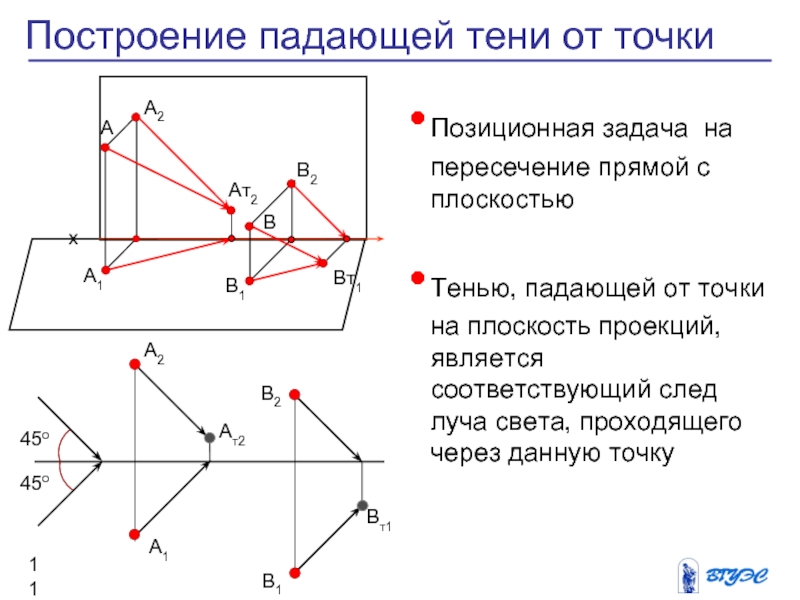
Слайд 11Позиционная задача на пересечение прямой с плоскостью
Тенью,
падающей от точки на плоскость проекций, является
соответствующий след луча света, проходящего через данную точку
Построение падающей тени от точки
x
A1
B1
A
A2
B
B2
Aт2
Bт1
45о
45о
В2
В1
Вт1
Ат2
А2
А1
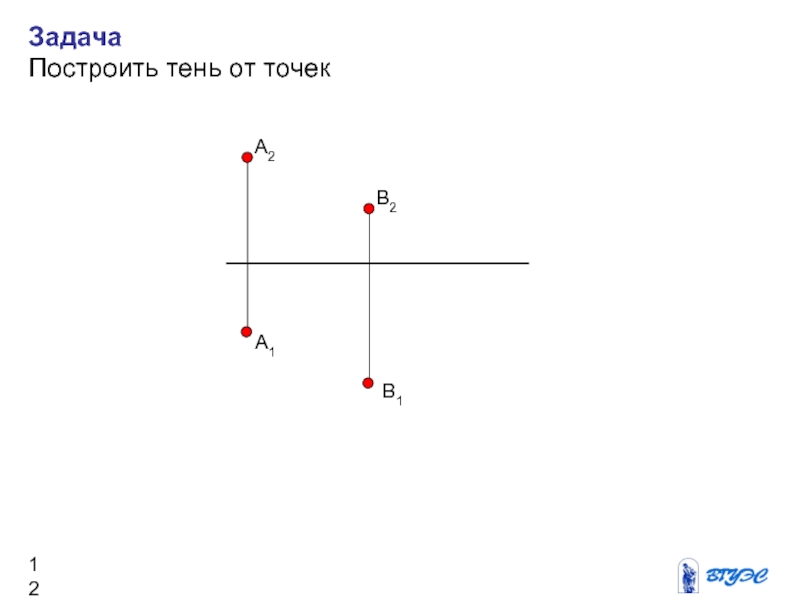
Слайд 12Задача
Построить тень от точек
A1
A2
В1
В2
Слайд 13Позиционная задача на пересечение прямой с плоскостью
Тенью,
падающей от точки на плоскость проекций, является
соответствующий след луча света, проходящего через данную точку
Построение падающей тени от точки
A1
A
A2
Aт2
Aт1
A1
A2
Ст2
(Aт1)

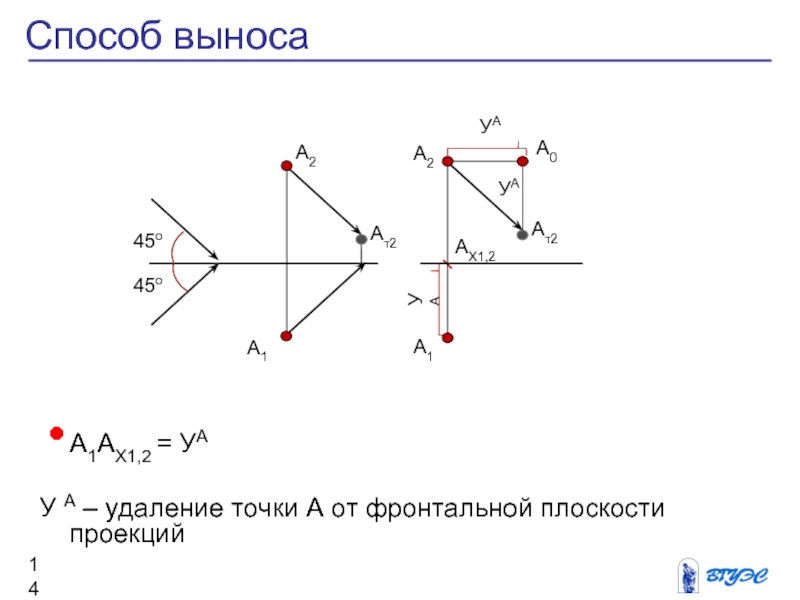
Слайд 14А1АХ1,2 = УА
У А – удаление точки
А от фронтальной плоскости проекций
Способ выноса
45о
45о
Ат2
А2
Ат2
А2
А1
УА
УА
А0
УА
А1
АХ1,2
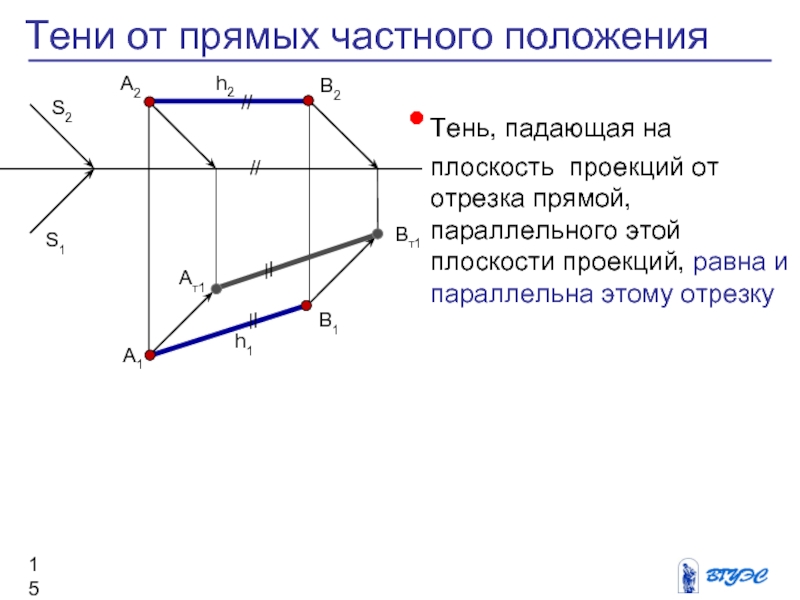
Слайд 15Тень, падающая на плоскость проекций от отрезка
прямой, параллельного этой плоскости проекций, равна и
параллельна этому отрезку
Тени от прямых частного положения
А2
А1
Ат1
Вт1
В2
В1
S2
S1
h2
h1
//
//
//
//
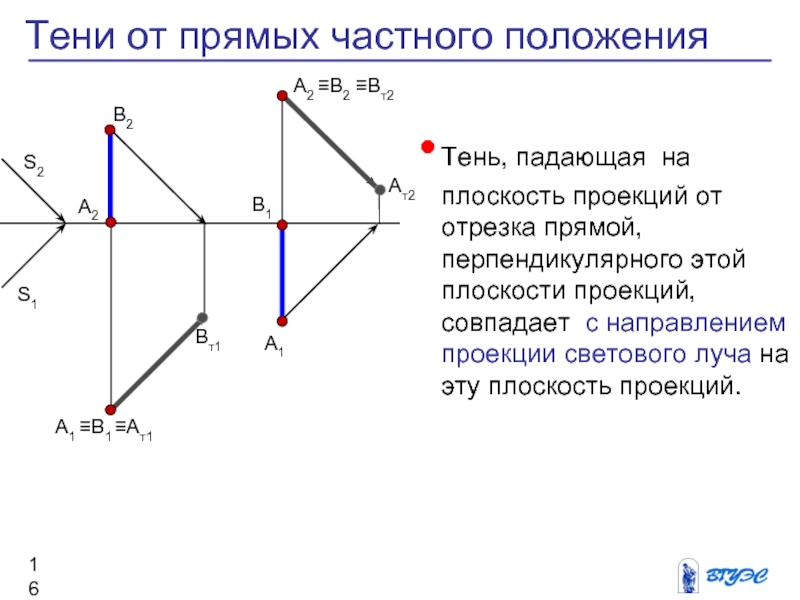
Слайд 16Тень, падающая на плоскость проекций от отрезка
прямой, перпендикулярного этой плоскости проекций, совпадает с
направлением проекции светового луча на эту плоскость проекций.
Тени от прямых частного положения
А2
А1 ≡В1
≡Ат1
Вт1
В2
S2
S1
А2 ≡В2
В1
А1
Ат2
≡Вт2
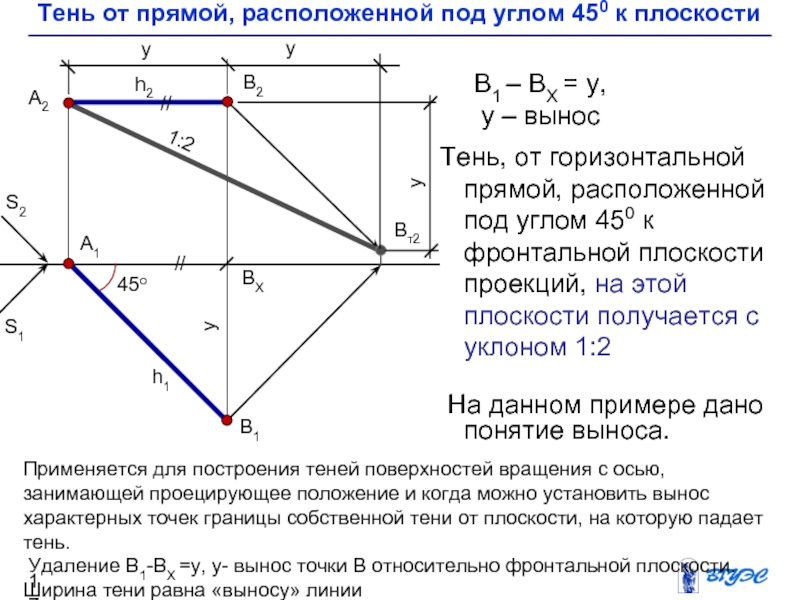
Слайд 17Тень, от горизонтальной прямой, расположенной под углом
450 к фронтальной плоскости проекций, на этой
плоскости получается с уклоном 1:2
На данном примере дано понятие выноса.
Тень от прямой, расположенной под углом 450 к плоскости
А2
А1
Вт2
В2
В1
S2
S1
h2
h1
//
//
y
y
y
y
1:2
ВХ
45о
В1 – ВХ = у,
у – вынос
Применяется для построения теней поверхностей вращения с осью, занимающей проецирующее положение и когда можно установить вынос характерных точек границы собственной тени от плоскости, на которую падает тень.
Удаление В1-ВХ =у, у- вынос точки В относительно фронтальной плоскости. Ширина тени равна «выносу» линии
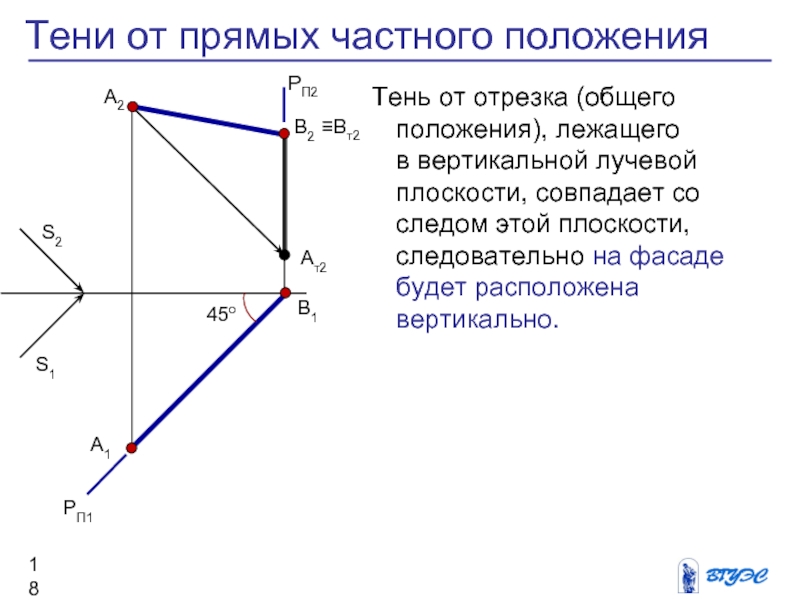
Слайд 18Тень от отрезка (общего положения), лежащего
в вертикальной лучевой плоскости, совпадает со следом этой плоскости, следовательно на фасаде будет расположена вертикально.
Тени от прямых частного положения
А2
≡Вт2
В2
В1
S2
S1
А1
Ат2
РП1
РП2
45о
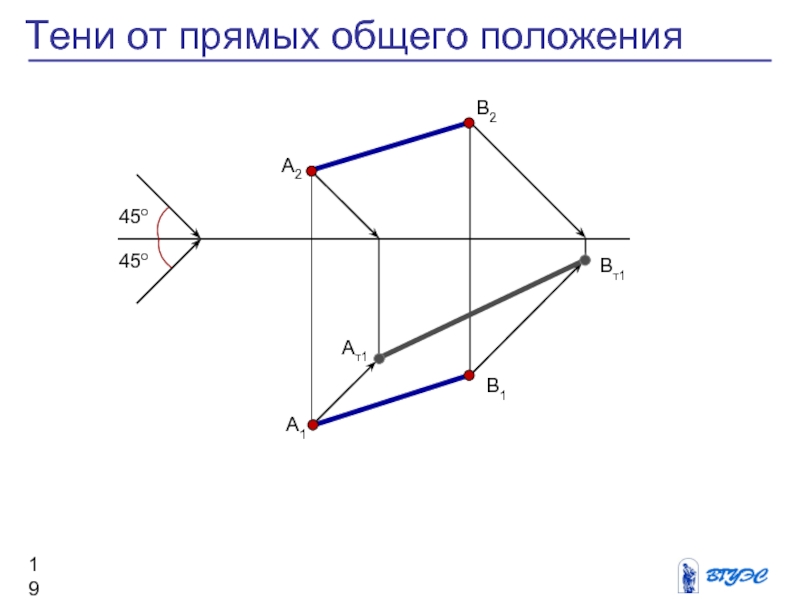
Слайд 19
Тени от прямых общего положения
45о
45о
А2
А1
Ат1
Вт1
В2
В1
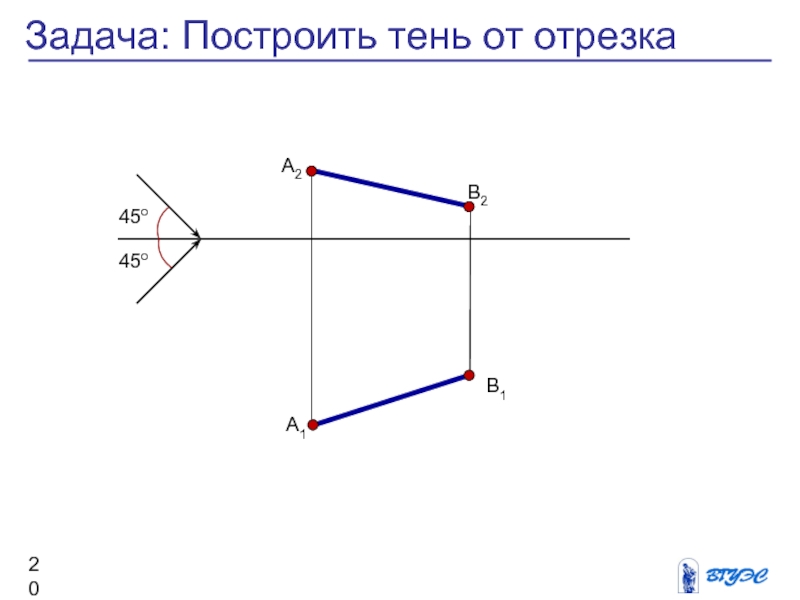
Слайд 20Задача: Построить тень от отрезка
45о
45о
А2
А1
В2
В1
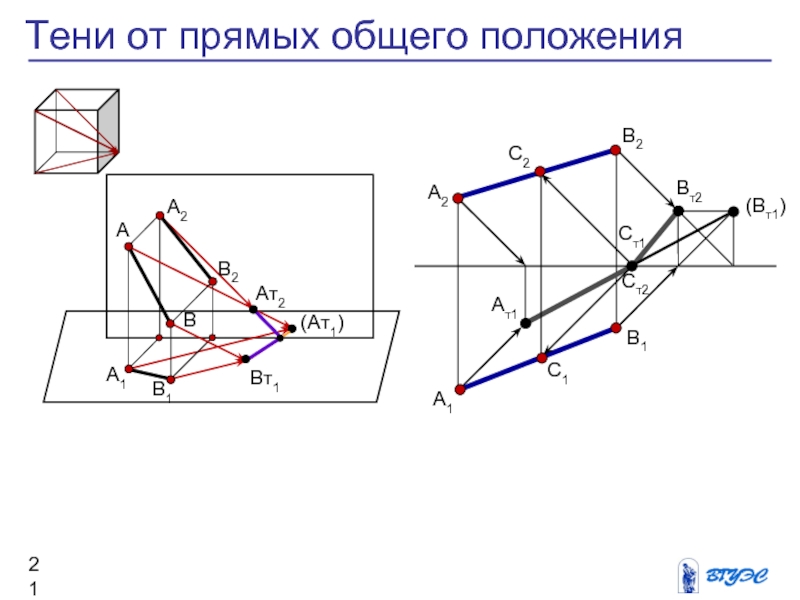
Слайд 21Тени от прямых общего положения
А2
А1
Ат1
Вт2
В2
В1
С1
(Вт1)
С2
Ст1
Ст2
A1
A
A2
Aт2
(Aт1)
B1
B
B2
Bт1
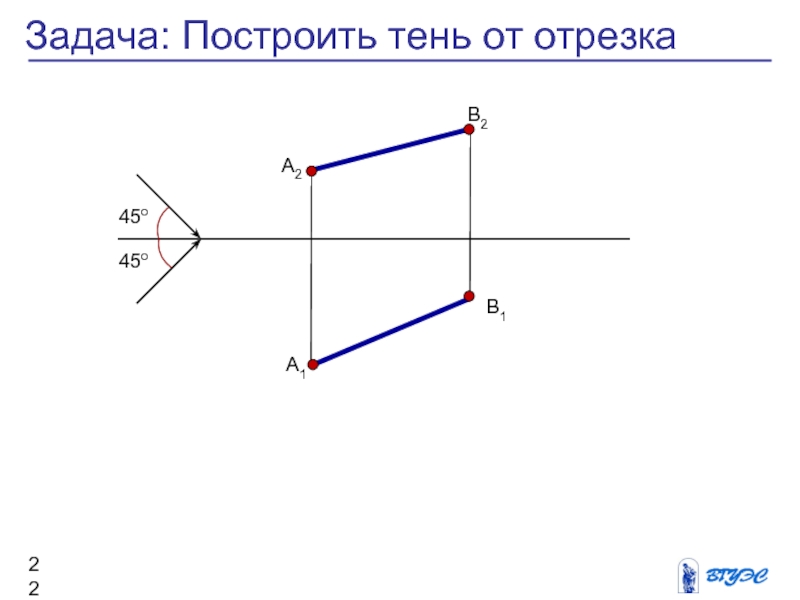
Слайд 22Задача: Построить тень от отрезка
45о
45о
А2
А1
В2
В1
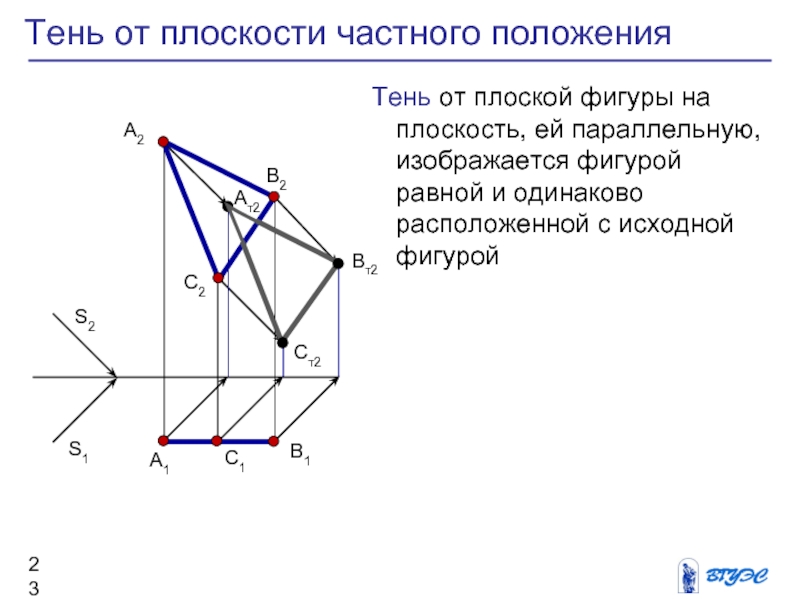
Слайд 23Тень от плоскости частного положения
А2
Вт2
В2
В1
S2
S1
А1
Ат2
С2
Ст2
С1
Тень от плоской
фигуры на плоскость, ей параллельную, изображается фигурой
равной и одинаково расположенной с исходной фигурой
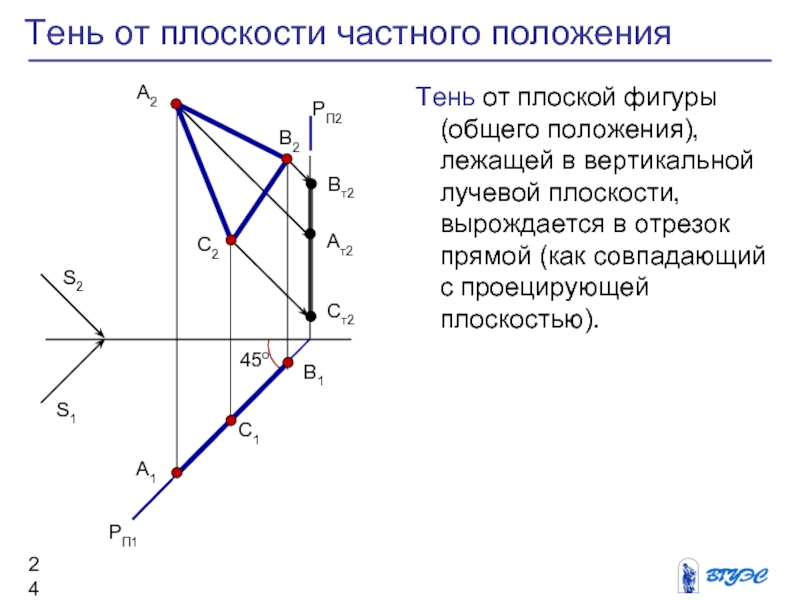
Слайд 24Тень от плоскости частного положения
Тень от плоской
фигуры (общего положения), лежащей в вертикальной лучевой
плоскости, вырождается в отрезок прямой (как совпадающий с проецирующей плоскостью).
А2
Вт2
В2
В1
S2
S1
А1
Ат2
РП1
РП2
45о
С2
Ст2
С1
Слайд 25
45о
45о
А2
А1
Ат1
Вт1
В2
В1
С2
С1
(Ст1)
Ст2
S2
S1
Тень от плоскости общего положения
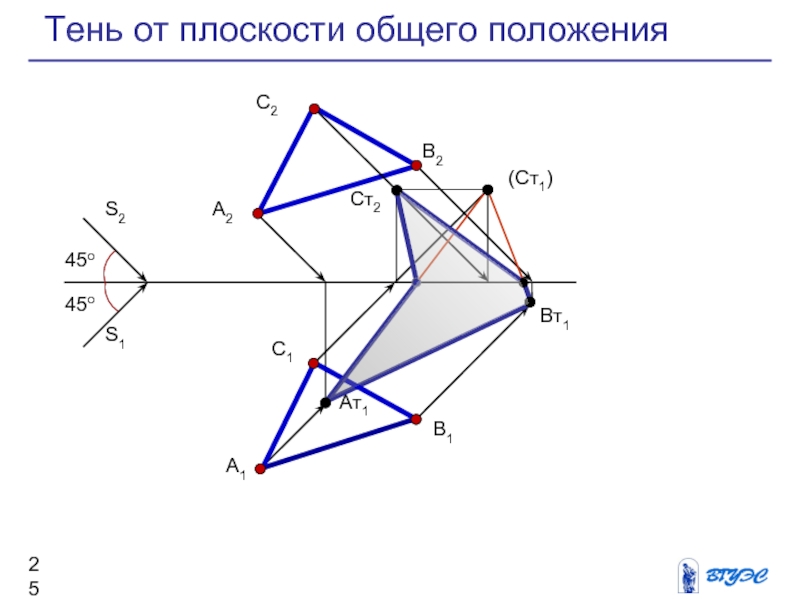
Слайд 26
45о
45о
А2
А1
В2
В1
С2
С1
S2
S1
Задача: Построить тень от плоскости
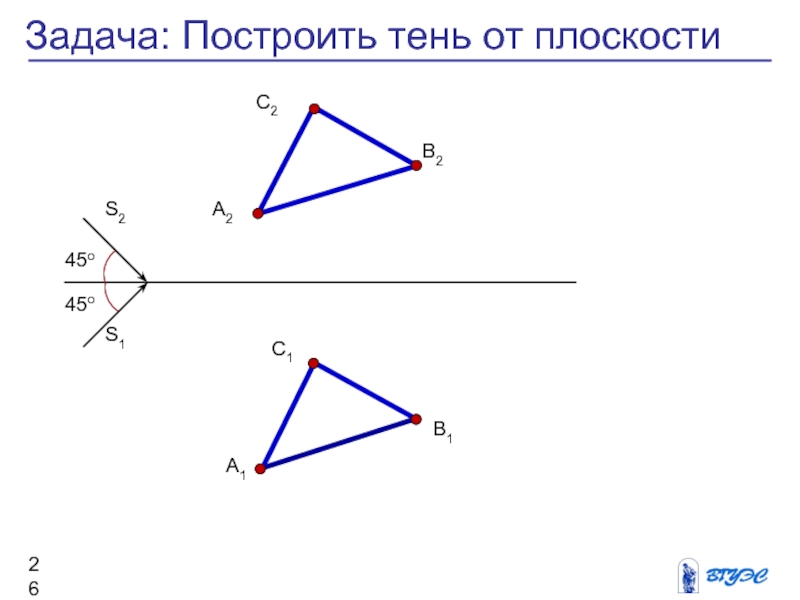
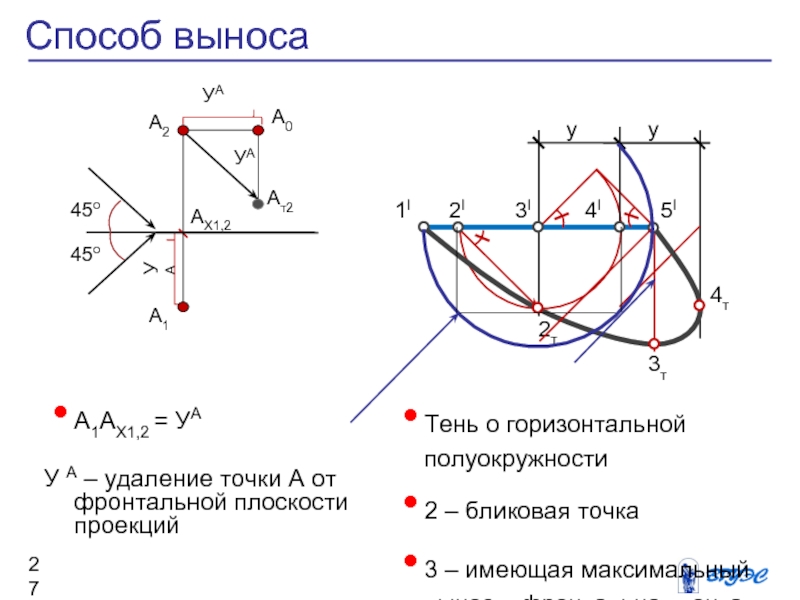
Слайд 27А1АХ1,2 = УА
У А – удаление точки
А от фронтальной плоскости проекций
Способ выноса
45о
45о
Ат2
А2
УА
УА
А0
УА
А1
АХ1,2
3I
1I
2I
4I
5I
у
у
2т
3т
4т
Тень о
горизонтальной полуокружности
2 – бликовая точка
3 – имеющая максимальный вынос – фронтальная точка
4 – теневая точка
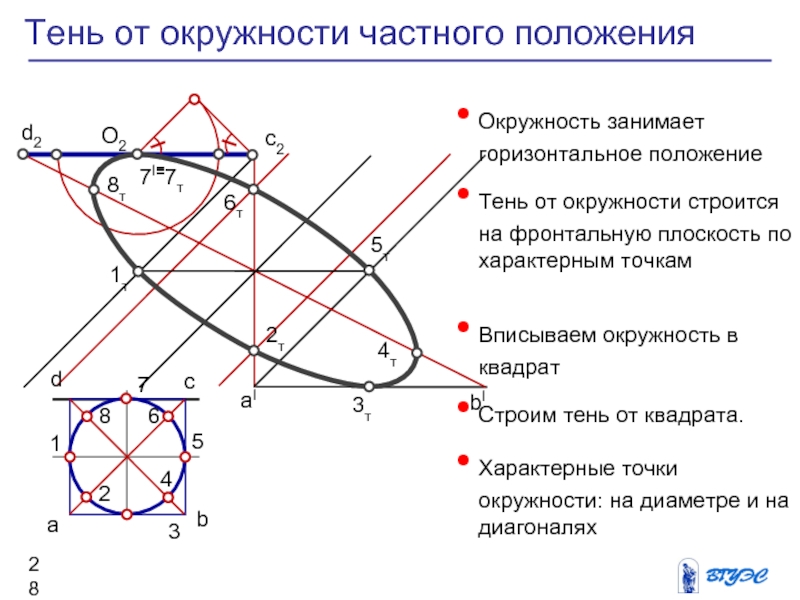
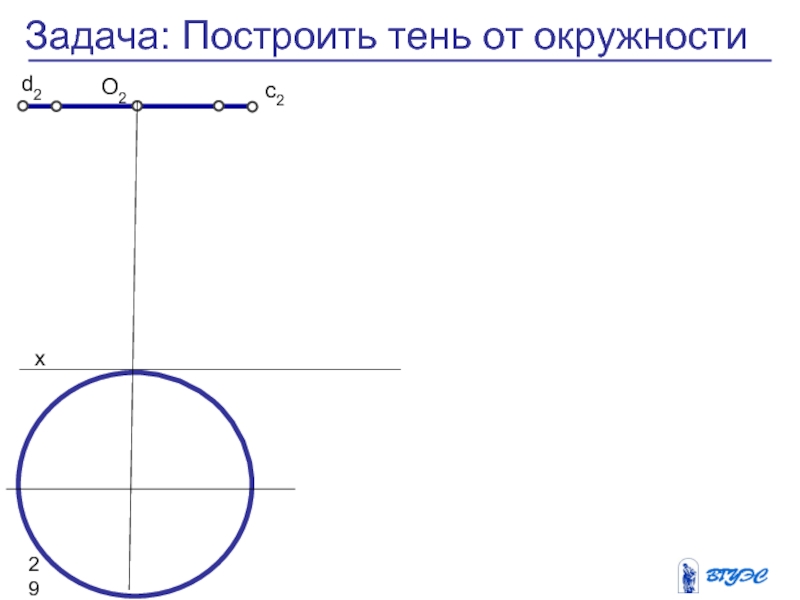
Слайд 28Тень от окружности частного положения
1
2
3
4
5
6
7
8
8т
3т
a
d
c
b
aI
bI
c2
d2
1т
2т
4т
5т
6т
О2
7I≡7т
Окружность занимает горизонтальное
положение
Тень от окружности строится на фронтальную плоскость
по характерным точкам
Вписываем окружность в квадрат
Строим тень от квадрата.
Характерные точки окружности: на диаметре и на диагоналях
Тень точек на диагоналях находятся из отношения стороны квадрата к диагонали =0,707
Слайд 29
c2
d2
О2
Задача: Построить тень от окружности
х
Слайд 30
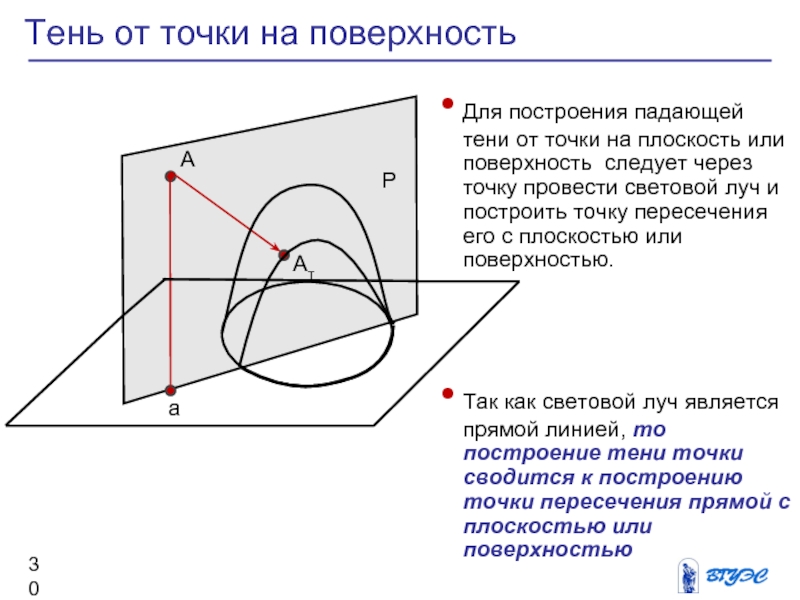
Тень от точки на поверхность
Для построения падающей
тени от точки на плоскость или поверхность
следует через точку провести световой луч и построить точку пересечения его с плоскостью или поверхностью.
Так как световой луч является прямой линией, то построение тени точки сводится к построению точки пересечения прямой с плоскостью или поверхностью
А
Ат
Р
а
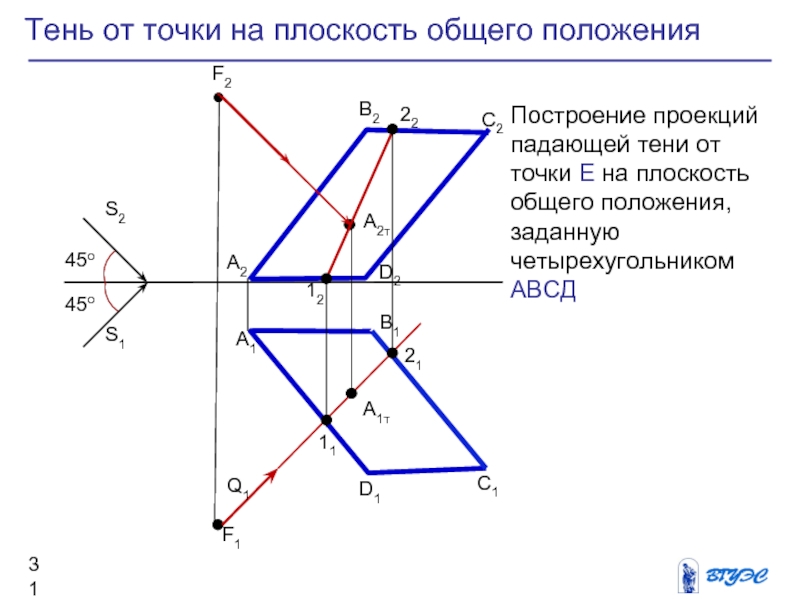
Слайд 31Тень от точки на плоскость общего положения
45о
45о
S2
S1
F2
С2
A2
A2т
B2
22
D2
12
A1
21
B1
D1
C1
A1т
11
F1
Q1
Построение
проекций падающей тени от точки Е на
плоскость общего положения, заданную четырехугольником АВСД
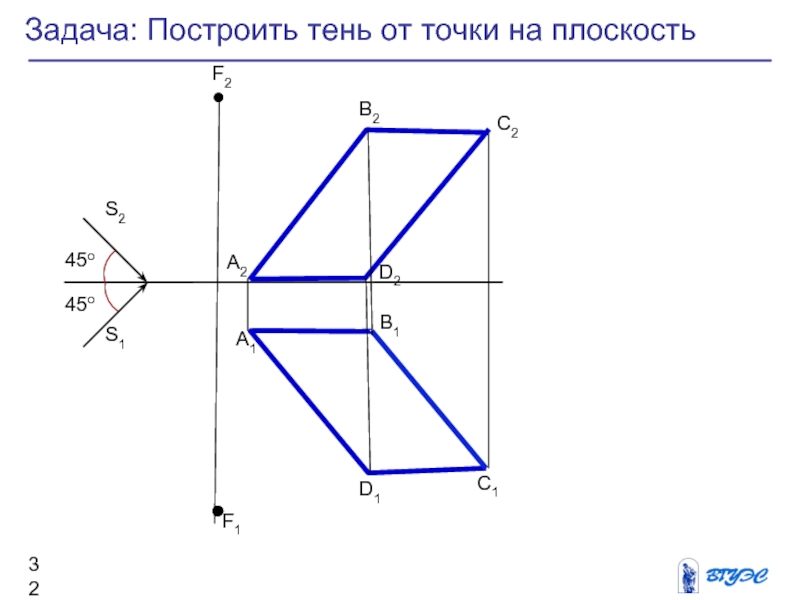
Слайд 32Задача: Построить тень от точки на плоскость
45о
45о
S2
S1
F2
С2
A2
B2
D2
A1
B1
D1
C1
F1
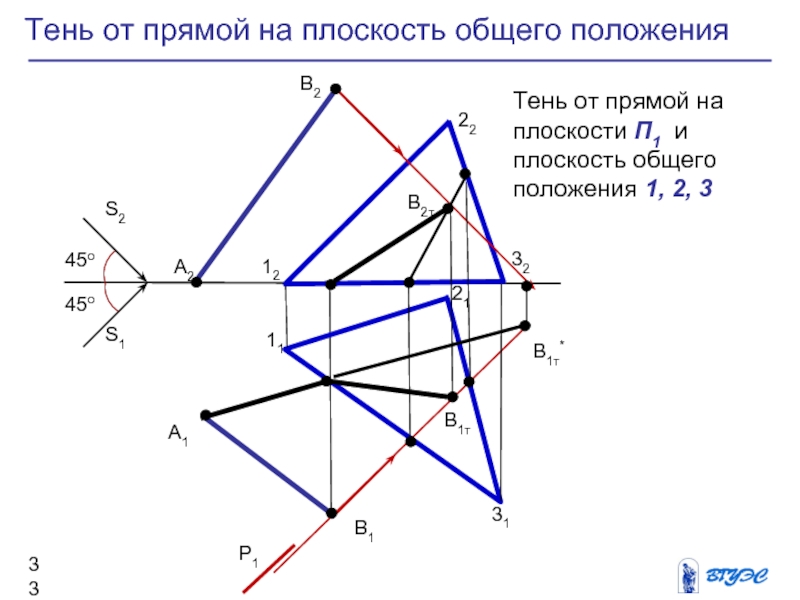
Слайд 33Тень от прямой на плоскость общего положения
45о
45о
S2
S1
Тень
от прямой на плоскости П1 и плоскость
общего положения 1, 2, 3
12
22
32
31
11
21
P1
A1
B1
B2
A2
B1т
B1т*
B2т
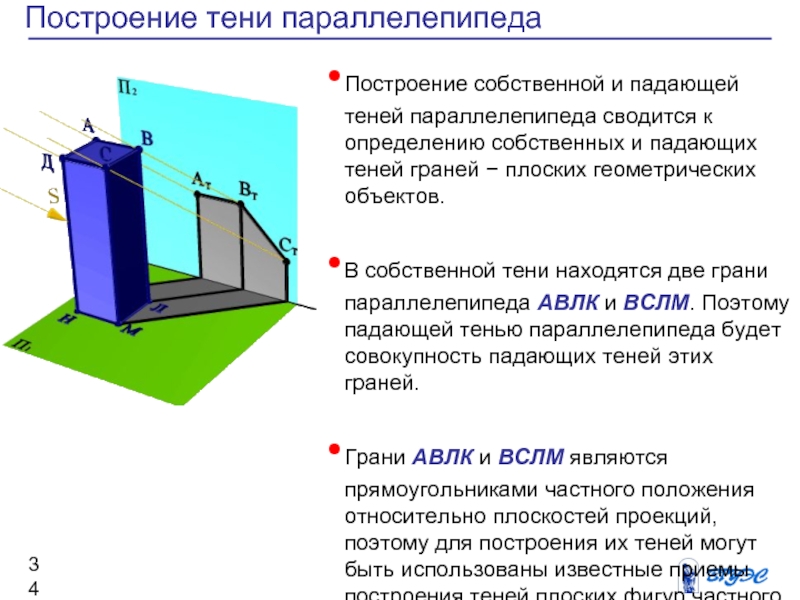
Слайд 34Построение тени параллелепипеда
Построение собственной и падающей теней
параллелепипеда сводится к определению собственных и падающих
теней граней − плоских геометрических объектов.
В собственной тени находятся две грани параллелепипеда АВЛК и ВСЛМ. Поэтому падающей тенью параллелепипеда будет совокупность падающих теней этих граней.
Грани АВЛК и ВСЛМ являются прямоугольниками частного положения относительно плоскостей проекций, поэтому для построения их теней могут быть использованы известные приемы построения теней плоских фигур частного положения.
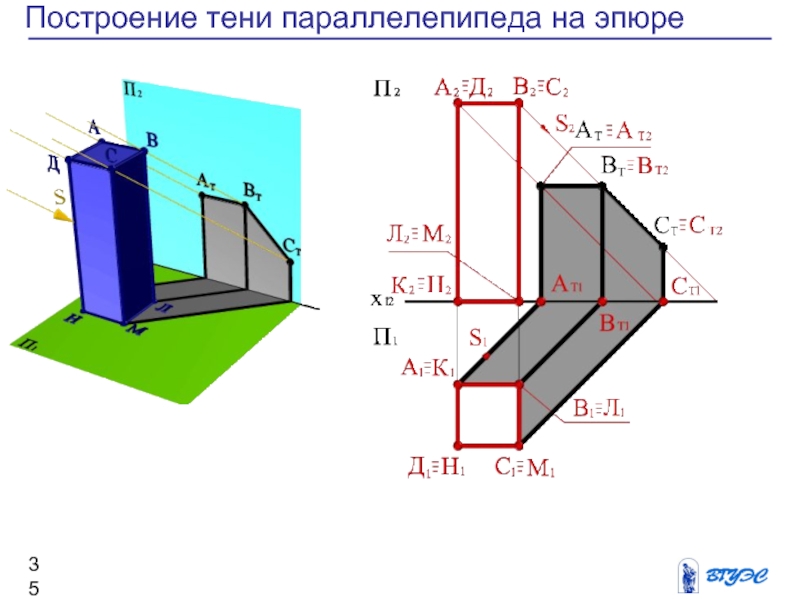
Слайд 35Построение тени параллелепипеда на эпюре
Слайд 36Построение тени пирамиды
Построение собственной и падающей теней
пирамиды сводится к определению собственных и падающих
теней граней − плоских геометрических объектов.
В собственной тени находится одна грань пирамиды АВД. Поэтому падающей тенью параллелепипеда будет падающая тень этой грани. Грань является треугольником общего положения относительно плоскостей проекций.
Сторона ВД лежит на горизонтальной плоскости проекций, т.е. совпадает со своей тенью.
Для нахождения теней отрезков АВ и АД требуется построить падающую действительную и мнимую тени точки А.

Слайд 37Построение тени пирамиды на эпюре

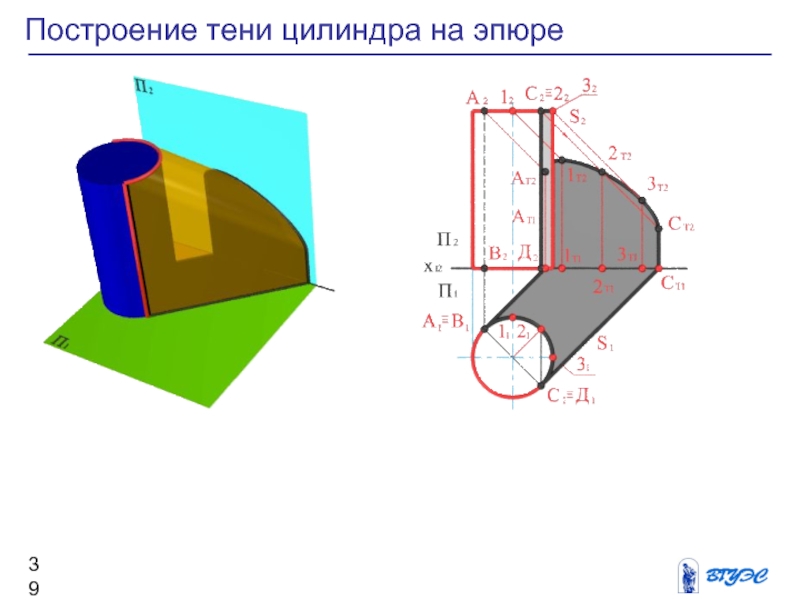
Слайд 38Построение тени цилиндра
Для определения контура собственной тени
прямого кругового конуса проведем две горизонтально проецирующие
лучевые плоскости, касательные к поверхности цилиндра и составляющие с фронтальной плоскостью проекций угол 45о.
Образующие АВ и СД, по которым плоскости касаются цилиндра, и полуокружности верхнего и нижнего оснований определяют контур собственной тени.
Падающая тень цилиндра ограничена тенью от контура собственной тени.
Тени от образующих строятся как тени вертикальных прямых.
Нижняя полуокружность совпадает с основанием цилиндра и расположена на горизонтальной плоскости.
Верхняя полуокружность строится как тень от сектора окружности, параллельной горизонтальной плоскости.

Слайд 39Построение тени цилиндра на эпюре
Слайд 40
S2
Задача: Построить тени цилиндра
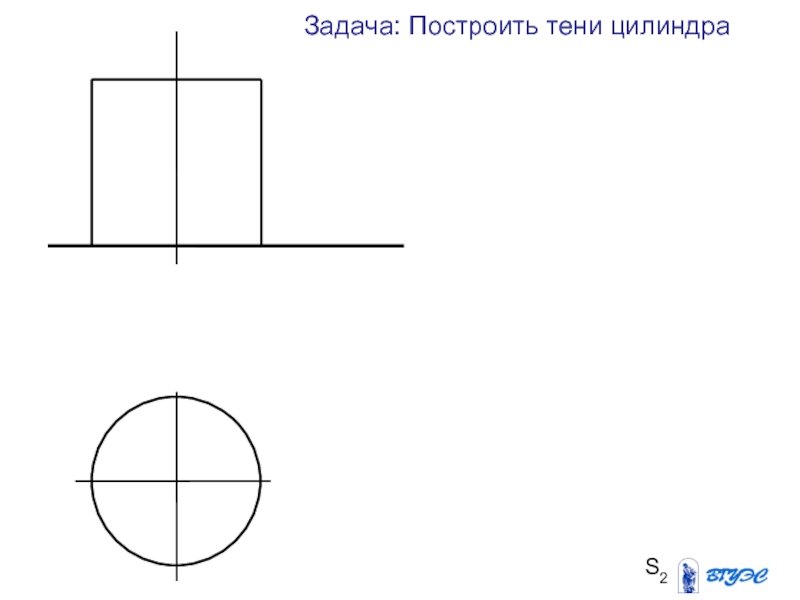
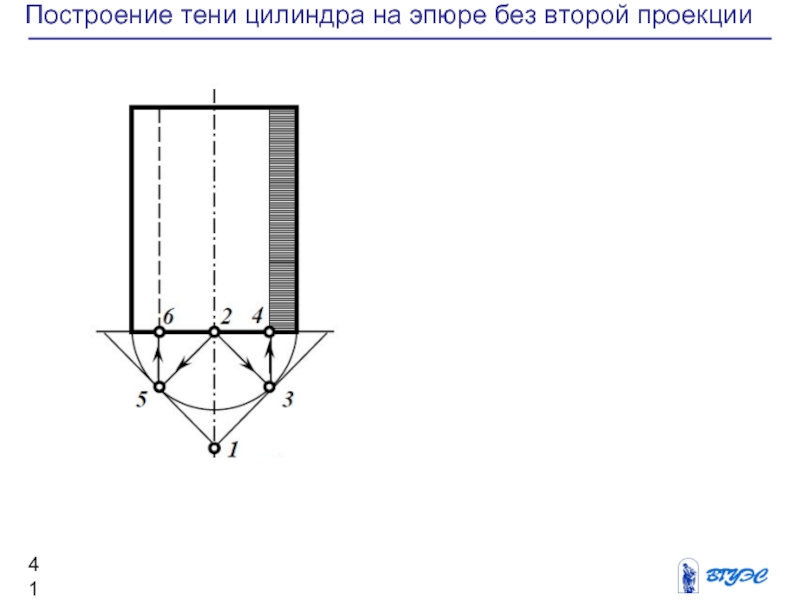
Слайд 41Построение тени цилиндра на эпюре без второй
проекции
Слайд 42
12
22
12I
32
2т2
3т2
1т2
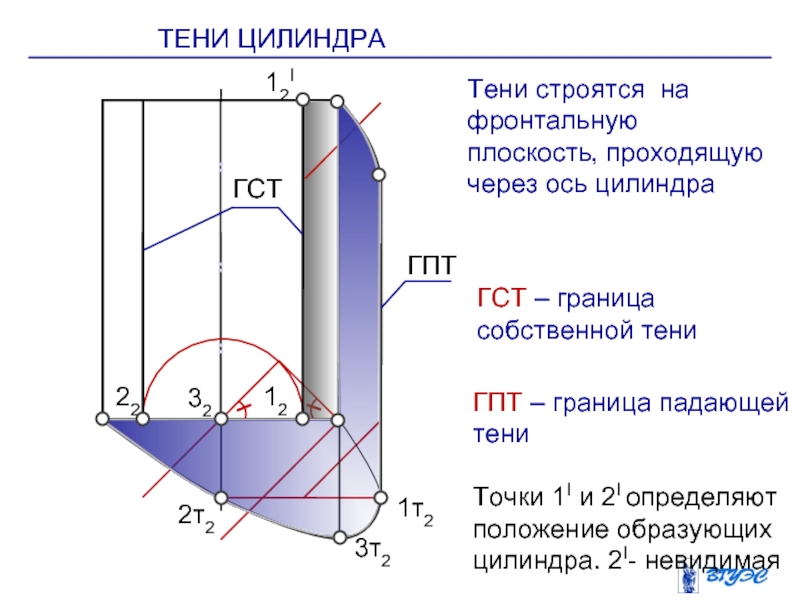
ТЕНИ ЦИЛИНДРА
ГСТ
ГСТ – граница собственной тени
ГПТ
ГПТ –
граница падающей тени
Точки 1I и 2I определяют
положение образующих цилиндра. 2I- невидимая
Тени строятся на фронтальную плоскость, проходящую через ось цилиндра
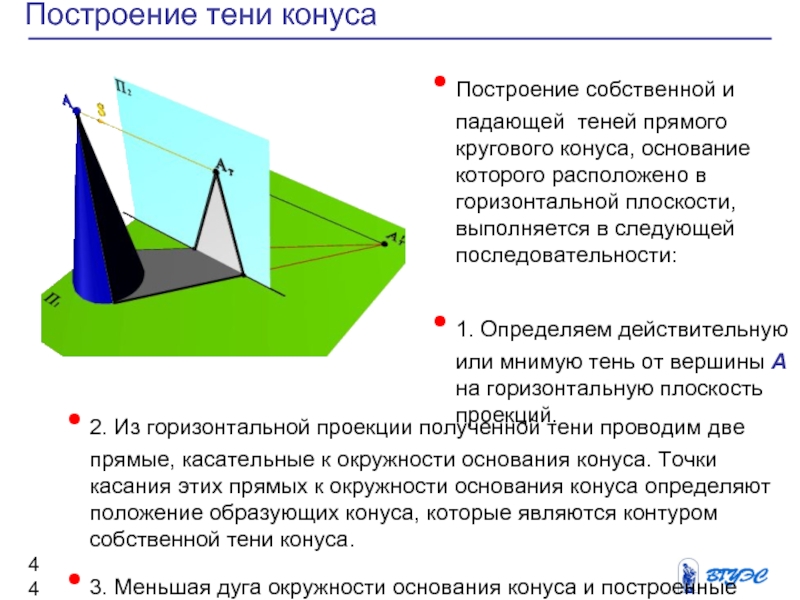
Слайд 44Построение тени конуса
Построение собственной и падающей теней
прямого кругового конуса, основание которого расположено в
горизонтальной плоскости, выполняется в следующей последовательности:
1. Определяем действительную или мнимую тень от вершины А на горизонтальную плоскость проекций.
2. Из горизонтальной проекции полученной тени проводим две прямые, касательные к окружности основания конуса. Точки касания этих прямых к окружности основания конуса определяют положение образующих конуса, которые являются контуром собственной тени конуса.
3. Меньшая дуга окружности основания конуса и построенные образующие определяют контур падающей тени.
Слайд 46
S1
S2
S2
Задача: Построить тени конуса
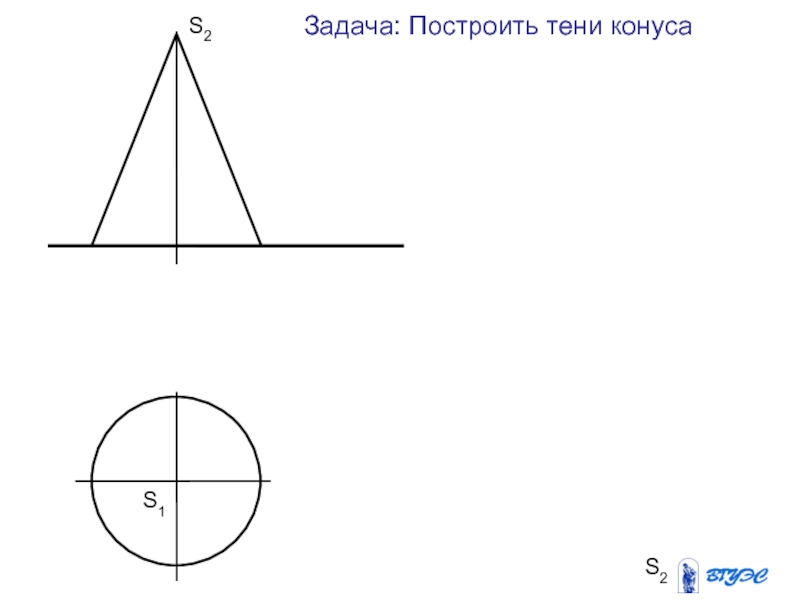
Слайд 47ТЕНЬ КОНУСА
с углом наклона образующей к
основанию равным 45О

Слайд 48Тень конуса с наклоном образующей 45°
У
конуса с наклоном образующей 45° фронтальная проекция
луча совпадает с очерковой образующей.
Собственная тень занимает одну четверть поверхности нижней полы конуса и три четверти поверхности верхней полы.
Теневыми образующими являются очерковая: правая фронтальная (S1) и профильная невидимая (S2).
У обратного – левая фронтальная и видимая профильная.
Касательным конусом с образующей под 45о будут определяться точки границы собственной тени на фронтальном и профильном очерках поверхности вращения.
21
S1
11
S1т
S2
22
12
Границей собственной тени у прямого 45о конуса являются образующие: правая фронтальная (S1) и профильная невидимая (S2)

Слайд 49Тень конуса с наклоном образующей 45°
S1т
S2
S1
31
41
О2
От1
3т1
4т1
≡42
Границей
собственной тени у обратного конуса – левая
фронтальная и видимая профильная
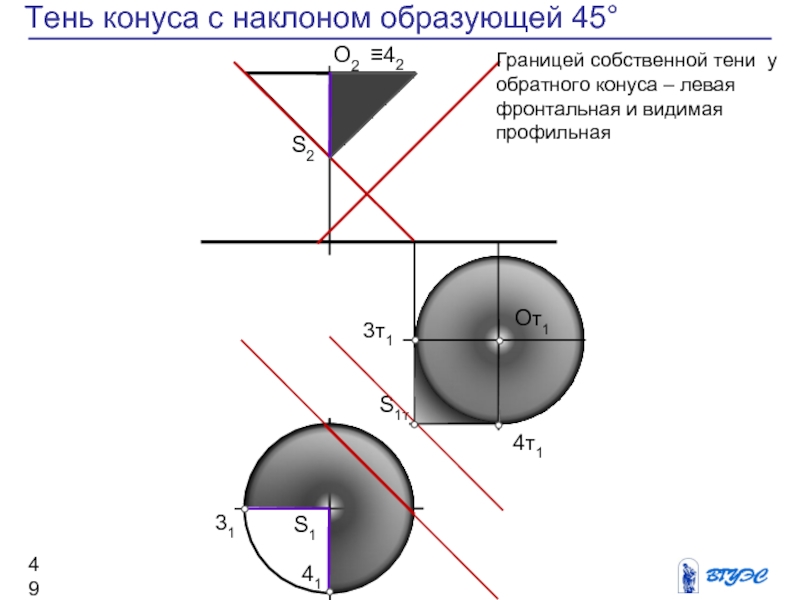
Слайд 50Касательным конусом с образующей под 45о будут
определяться точки границы собственной тени на фронтальном
и профильном очерках поверхности вращения

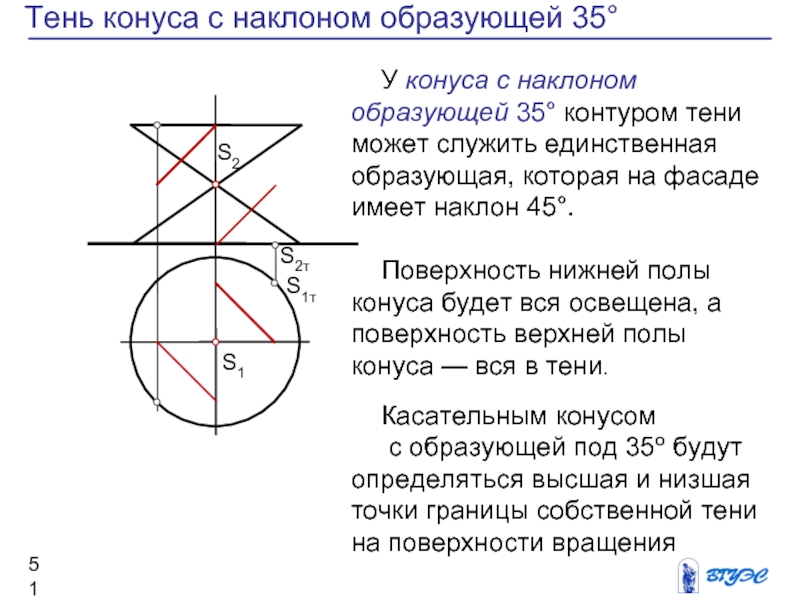
Слайд 51Тень конуса с наклоном образующей 35°
S1
S1т
S2
S2т
У
конуса с наклоном образующей 35° контуром тени
может служить единственная образующая, которая на фасаде имеет наклон 45°.
Поверхность нижней полы конуса будет вся освещена, а поверхность верхней полы конуса — вся в тени.
Касательным конусом
с образующей под 35о будут определяться высшая и низшая точки границы собственной тени на поверхности вращения
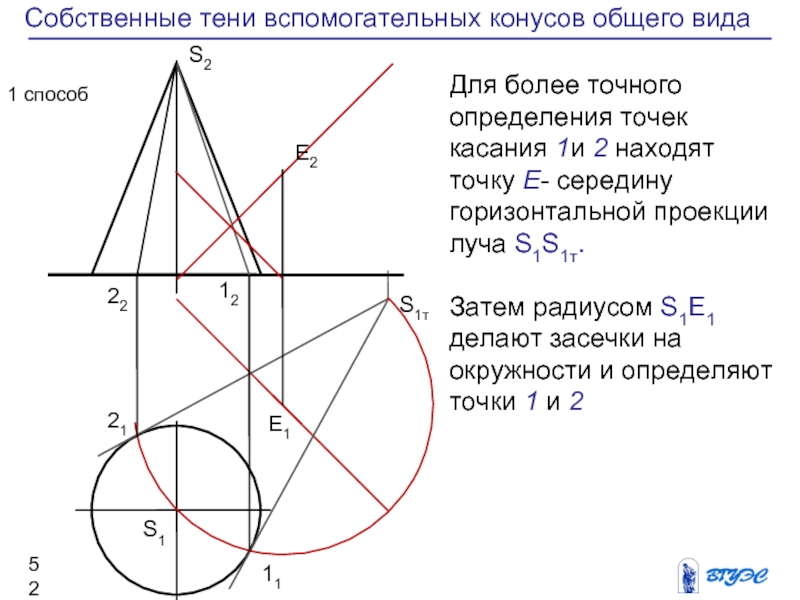
Слайд 52Собственные тени вспомогательных конусов общего вида
21
S1
11
S1т
S2
Е1
22
12
Е2
1 способ
Для
более точного определения точек касания 1и 2
находят точку Е- середину горизонтальной проекции луча S1S1т.
Затем радиусом S1Е1 делают засечки на окружности и определяют точки 1 и 2
Слайд 53Собственные тени вспомогательных конусов общего вида
S2
S2
12
12
22
22
Е2
Е2
2 способ
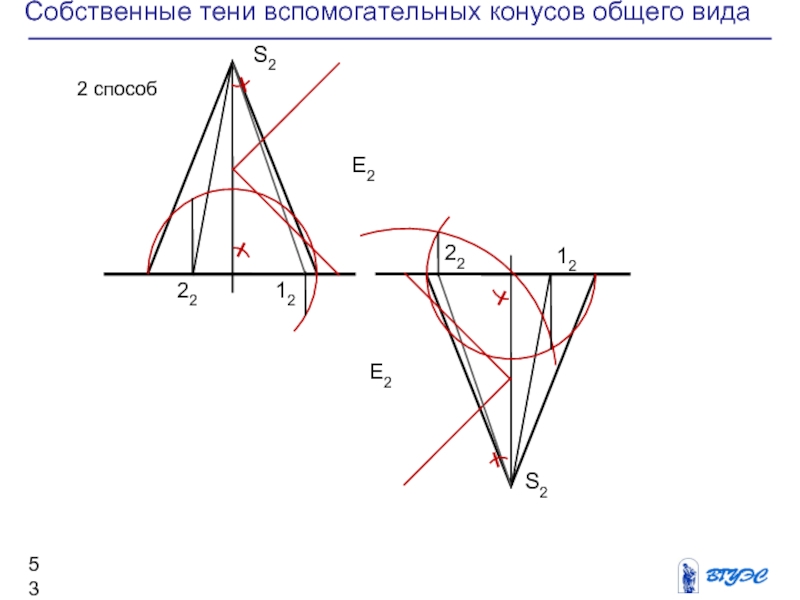
Слайд 54Собственные тени вспомогательных конусов общего вида
S2
42
12
22
32
1т2
2т2
3т2
4т2
А2
В2
Ат2≡
≡Вт2
3 способ
Тени
строятся на фронтальную плоскость, проходящую через ось
конуса.
Из точки тени от вершины конуса проводится касательная к тени основания.
«Обратным» лучом из точки 4т2 находим точку 42 и образующую S242, которая будет являться контуром собственной тени и Sт24т23т22т21т2Aт2- контур падающей тени
К совмещенной с фасадом окружности основания проводят горизонтальную касательную до точки пересечения с продолжением очерковой образующей. Из полученной точки проводят луч под углом в 45о, которая пересекаясь с окружностью, дает необходимые точки 11 и 21.
Их проекции 12 и 22 определят положение границы собственной тени
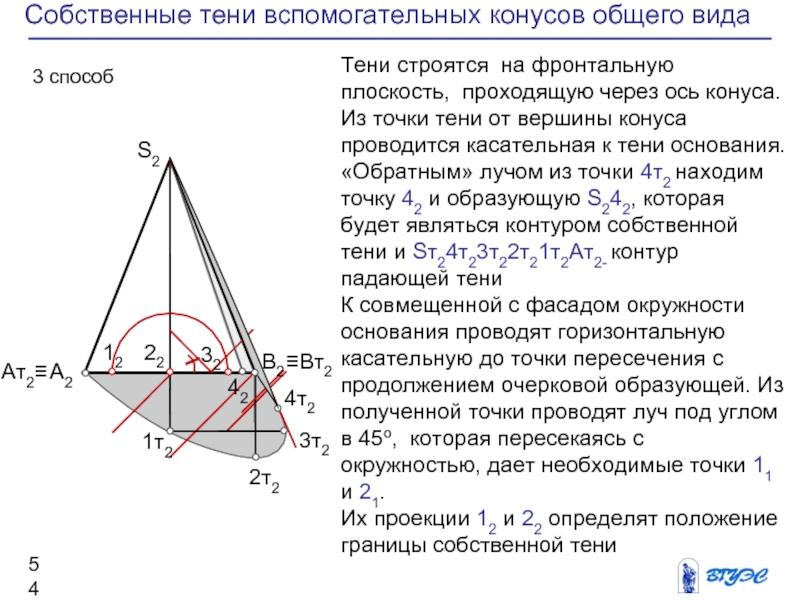
Слайд 55Собственные тени вспомогательных конусов общего вида
3 способ
S2
12
22
N2
21
11
11
S2
12
22
N2
21
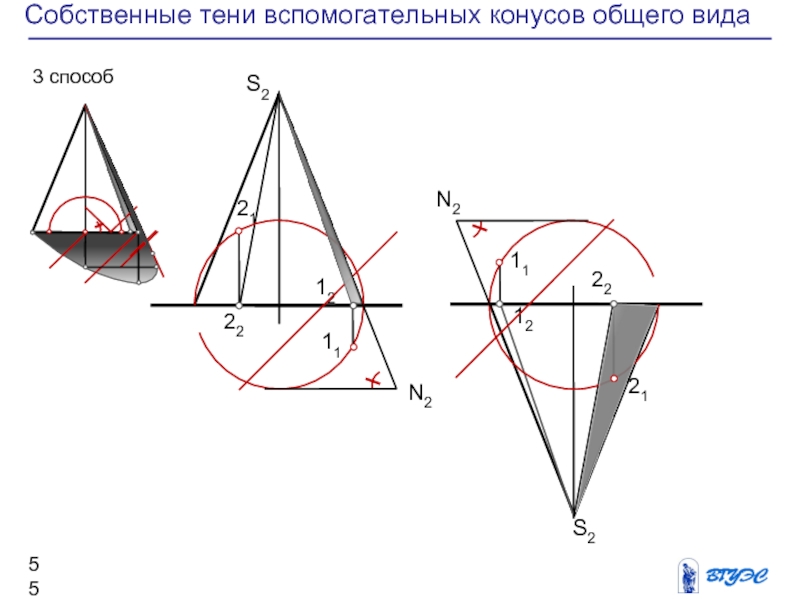
Слайд 56Построение тени конуса на эпюре без второй
проекции
Для определения тени на конусе нужно построить
к его фронтальной проекции половину горизонтальной проекции.
Из точки 1 полуокружности проведем прямую 1–2 параллельно проекции левой очерковой образующей конуса до пересечения с горизонтальным диаметром в точке 2.
Через точку 2 построим прямую под углом 45° к диаметру, и отметим точку 3 пересечения прямой с окружностью.
Проведем через точку 3 вертикальную прямую, найдем точку 4, через которую проходит видимая граница собственной тени конуса.
Если провести через точку 2 прямую 2–5 также под углом 45° к диаметру, а через точку 5 – вертикальную прямую, то получим точку 6, через которую проходит невидимая граница собственной тени.
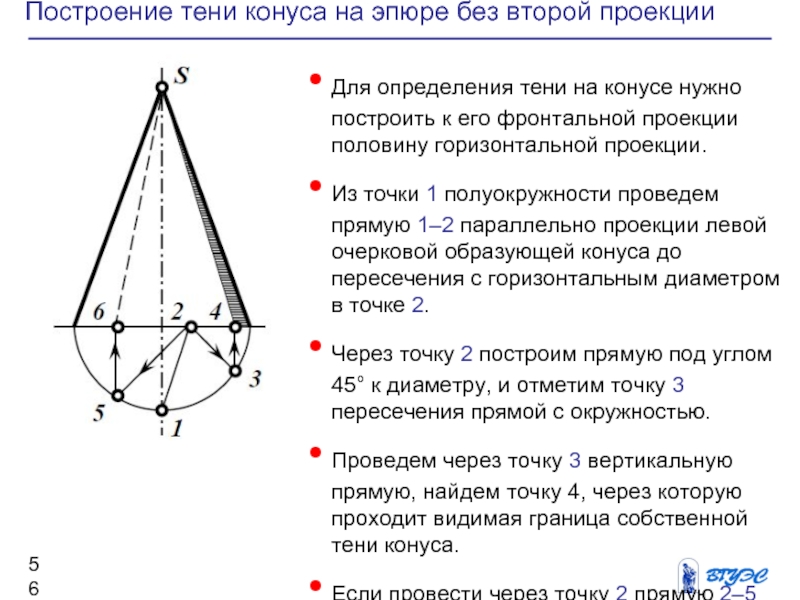
Слайд 57Построение собственной тени сферы
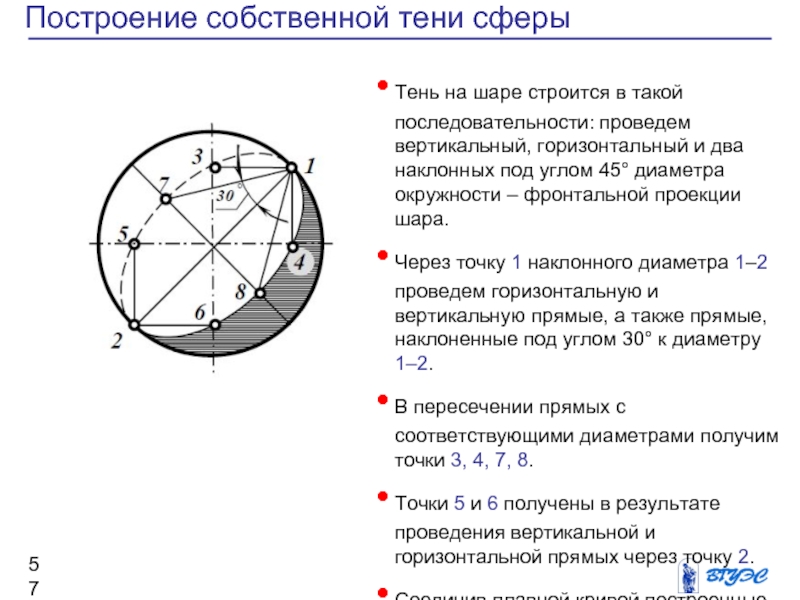
Тень на шаре строится
в такой последовательности: проведем вертикальный, горизонтальный и
два наклонных под углом 45° диаметра окружности – фронтальной проекции шара.
Через точку 1 наклонного диаметра 1–2 проведем горизонтальную и вертикальную прямые, а также прямые, наклоненные под углом 30° к диаметру 1–2.
В пересечении прямых с соответствующими диаметрами получим точки 3, 4, 7, 8.
Точки 5 и 6 получены в результате проведения вертикальной и горизонтальной прямых через точку 2.
Соединив плавной кривой построенные точки, получим эллипс – фронтальную проекцию границы собственной тени шара (половина эллипса невидима).
Слайд 58Построение падающей тени сферы
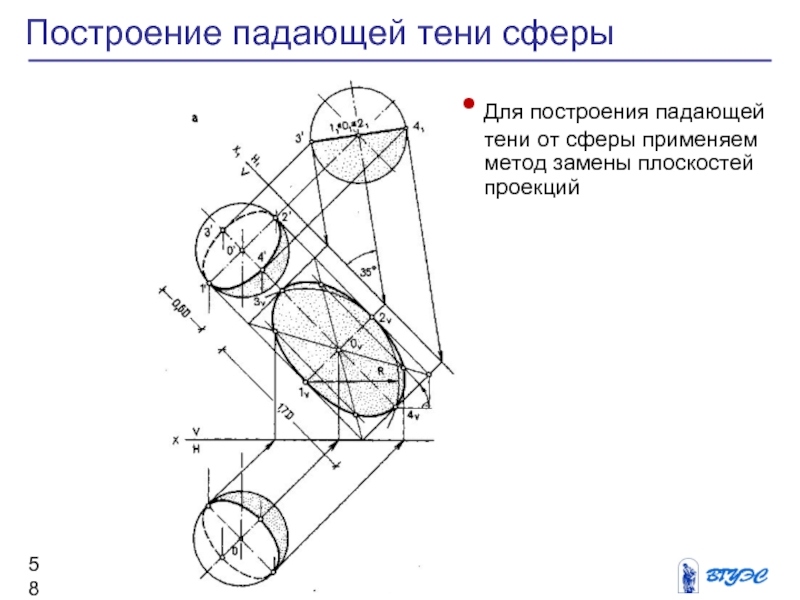
Для построения падающей
тени от сферы применяем метод замены плоскостей
проекций
Слайд 59Способ обратных лучей
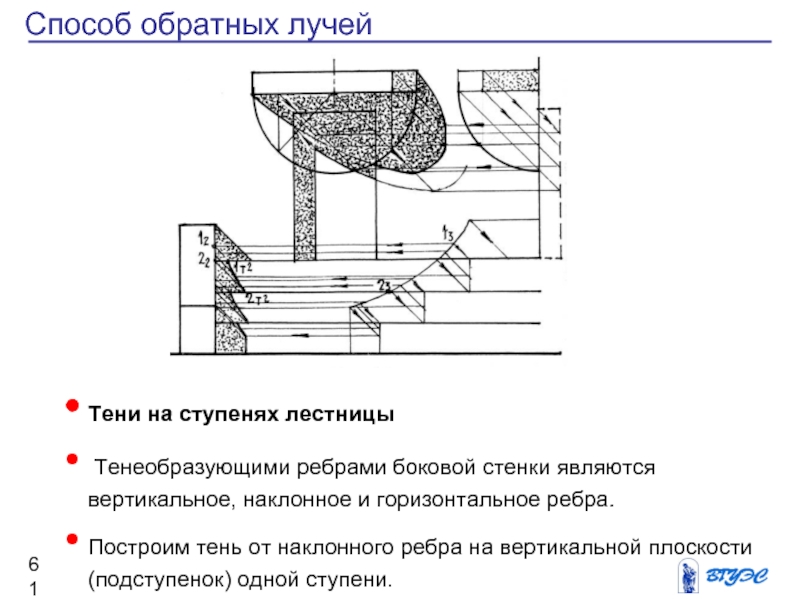
Тени на ступенях лестницы
Тенеобразующими ребрами боковой стенки являются вертикальное, наклонное
и горизонтальное ребра.
Вертикальное ребро повторяет профиль лестницы до точки а0.
Тень от горизонтального ребра совпадает с проекцией луча.

Слайд 60Способ обратных лучей
Построим тень от наклонного ребра
АВ на вертикальной плоскости (подступенок) одной ступени.
Проведем
профильные проекции обратных лучей, затем построим на фасаде тени 10 и 20.
Так как наклонное ребро АВ параллельно наклону лестничного марша, проекции точек тени, аналогичные построенным, будут располагаться на остальных ступенях на вертикальных прямых.

Слайд 61Способ обратных лучей
Тени на ступенях лестницы
Тенеобразующими ребрами боковой стенки являются вертикальное, наклонное
и горизонтальное ребра.
Построим тень от наклонного ребра на вертикальной плоскости (подступенок) одной ступени.
Проведем профильные проекции обратных лучей, затем построим на фасаде тени 12т и 22т.
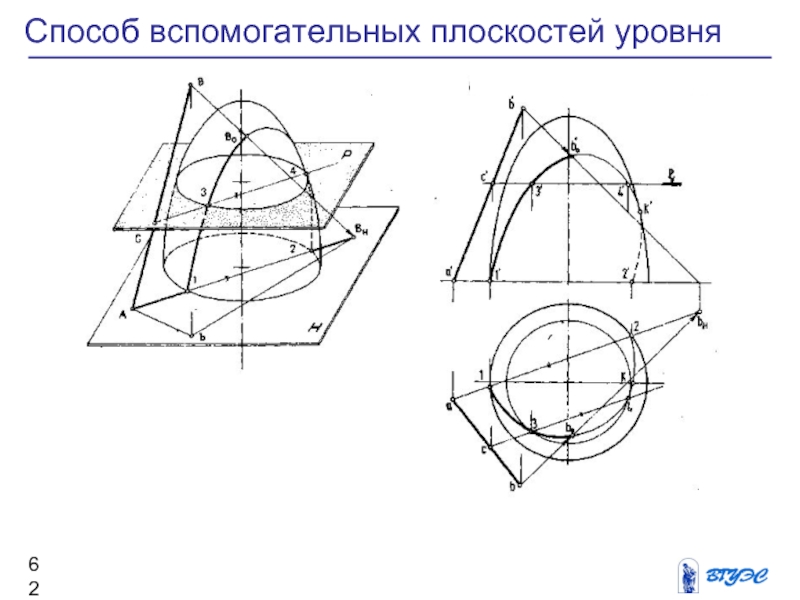
Слайд 62Способ вспомогательных плоскостей уровня
Слайд 63
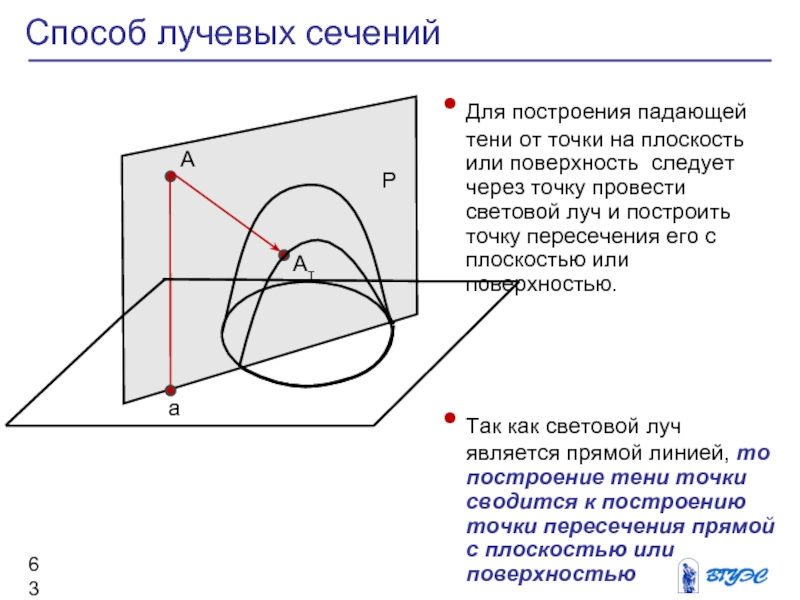
Способ лучевых сечений
Для построения падающей тени от
точки на плоскость или поверхность следует через
точку провести световой луч и построить точку пересечения его с плоскостью или поверхностью.
Так как световой луч является прямой линией, то построение тени точки сводится к построению точки пересечения прямой с плоскостью или поверхностью
А
Ат
Р
а
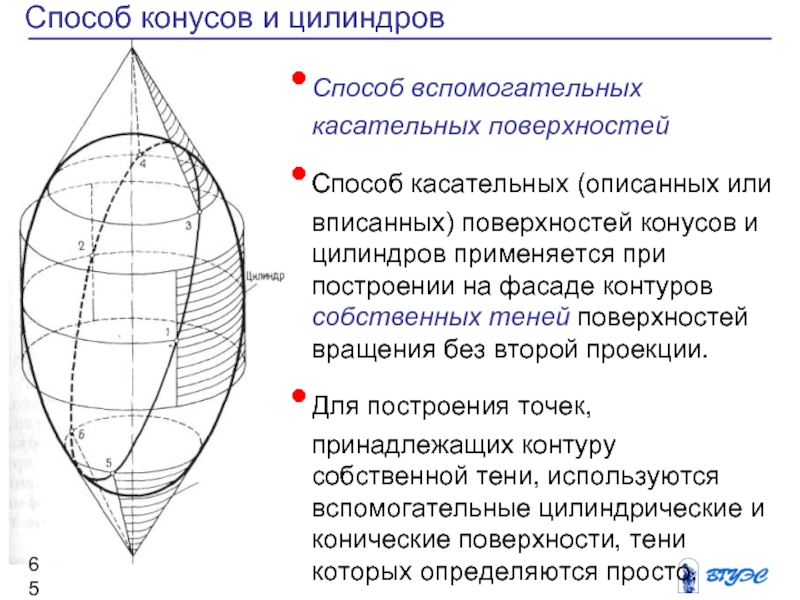
Слайд 65Способ конусов и цилиндров
Способ вспомогательных касательных поверхностей
Способ
касательных (описанных или вписанных) поверхностей конусов и
цилиндров применяется при построении на фасаде контуров собственных теней поверхностей вращения без второй проекции.
Для построения точек, принадлежащих контуру собственной тени, используются вспомогательные цилиндрические и конические поверхности, тени которых определяются просто.
Эти поверхности касаются заданной поверхности вращения по окружностям — параллелям.
Слайд 66Способ конусов и цилиндров
Сначала применяют вспомогательные цилиндрические
поверхности, которые касаются поверхности вращения по экватору
или горловине, затем применяют касательные конусы, соосные с данной поверхностью.
После этого определяют теневые образующие вспомогательных поверхностей и отмечают точки их соприкосновения с соответствующими параллелями данной поверхности. Эти точки принадлежат контуру собственной тени поверхности вращения. Полученные точки тени соединяют плавной кривой.
При построении контура собственной тени прежде всего необходимо построить характерные точки контура — точки тени, лежащие на фронтальном и профильном очерках поверхности (точки видимости), а также высшую и низшую точки контура тени.
Первые две точки определяют с помощью касательных конусов с углом наклона образующей 45°, а вторые две точки — с помощью конусов с углом наклона образующей 35 °

Слайд 67Построение собственной тени поверхности вращения
35о
45о
35о
45о
450
450
350
350
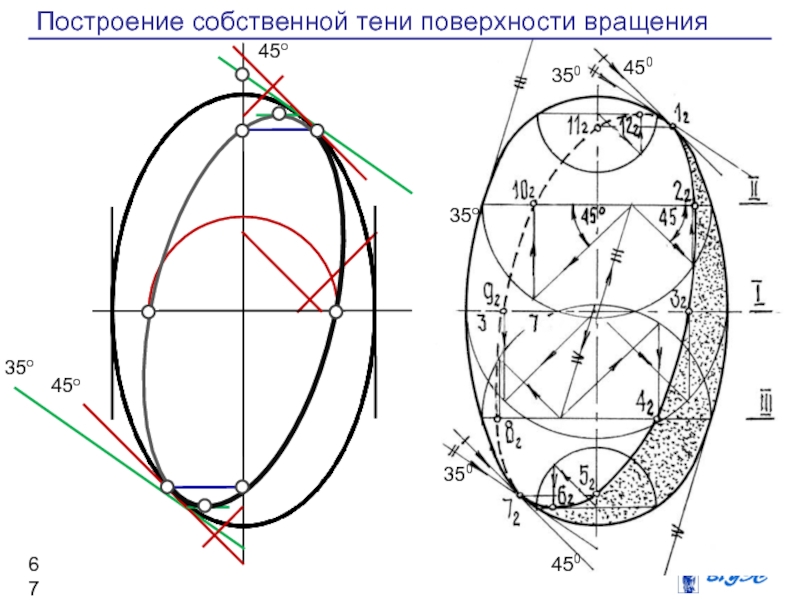
Слайд 68Построение собственной тени поверхности вращения
Применяя перечисленные выше
“стандартные” приемы построения теней цилиндра и конусов,
можно построить необходимое число точек контура собственной тени любой поверхности вращения.
Рассмотрим пример построения контура собственной тени выпуклой поверхности вращения — о в о и д а.
Для построения точек тени на экваторе поверхности опишем вокруг поверхности соосный цилиндр и на окружности касания определим общие точки тени 1′ и 2′.
Затем построим фронтальные проекции вспомогательных касательных конусов с углом наклона образующей 35°, проведя касательные к очерку овоида до пересечения с осью, а из этой точки — прямую под углом 45° к линии касания, получим высшую точку 3′ (невидимую) и низшую 4′.
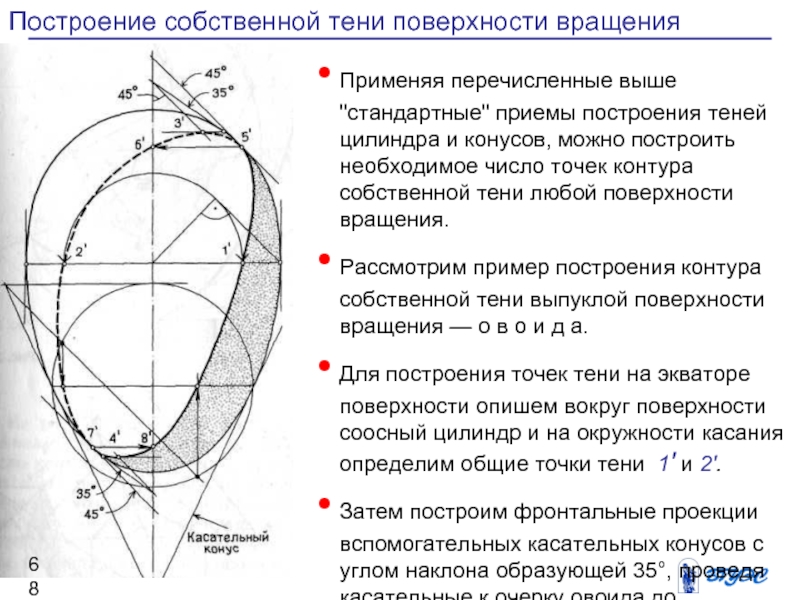
Слайд 69Построение собственной тени поверхности вращения
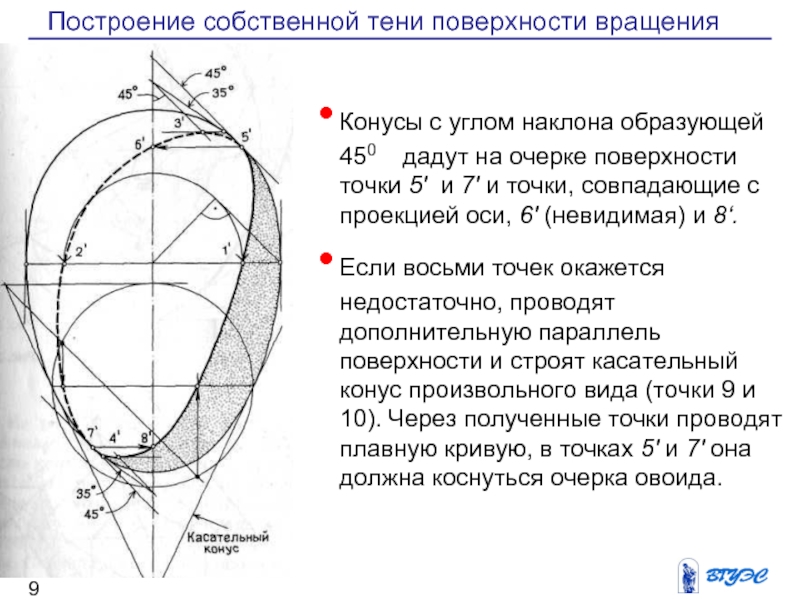
Конусы с углом
наклона образующей 450 дадут на очерке
поверхности точки 5′ и 7′ и точки, совпадающие с проекцией оси, 6′ (невидимая) и 8‘.
Если восьми точек окажется недостаточно, проводят дополнительную параллель поверхности и строят касательный конус произвольного вида (точки 9 и 10). Через полученные точки проводят плавную кривую, в точках 5′ и 7′ она должна коснуться очерка овоида.
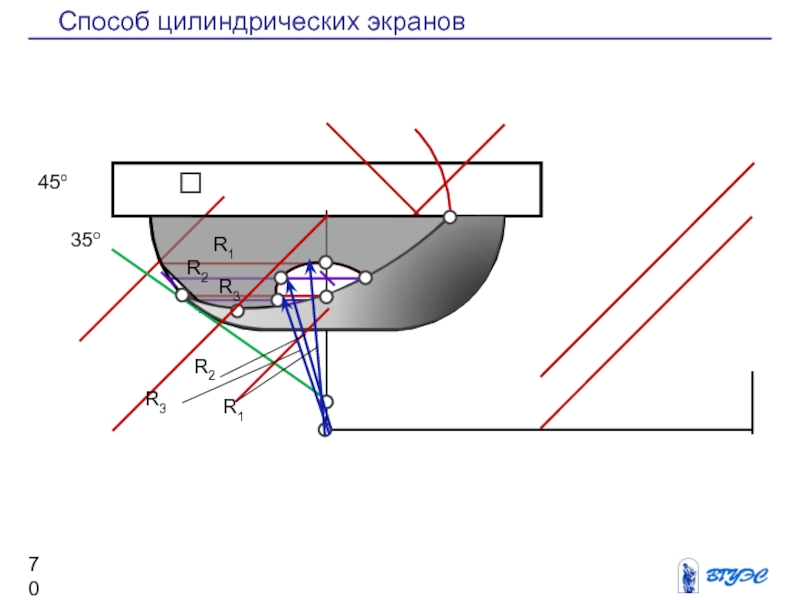
Слайд 70Способ цилиндрических экранов
35о
45о
R1
R2
R3
R2
R1
R3
Слайд 71
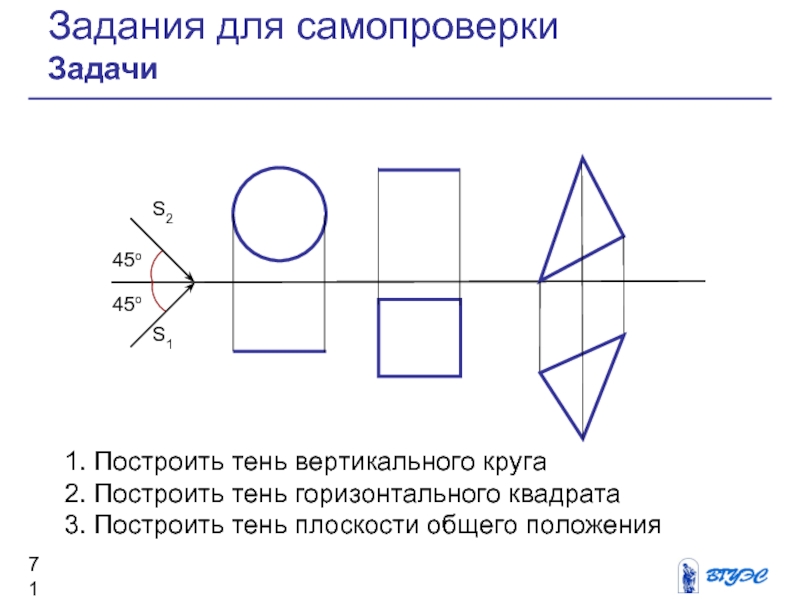
1. Построить тень вертикального круга
2. Построить тень
горизонтального квадрата
3. Построить тень плоскости общего положения
Задания
для самопроверки
Задачи
45о
45о
S2
S1
Слайд 72
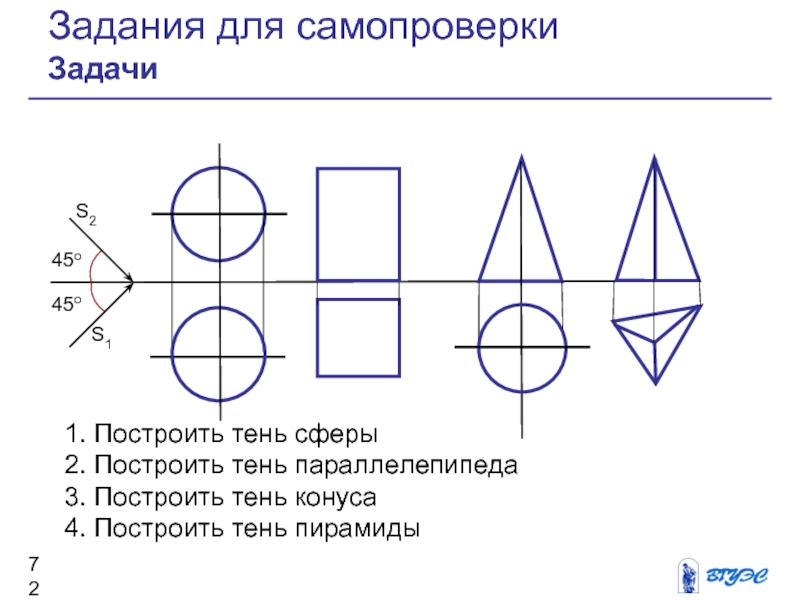
1. Построить тень сферы
2. Построить тень параллелепипеда
3.
Построить тень конуса
4. Построить тень пирамиды
Задания для
самопроверки
Задачи
45о
45о
S2
S1
Комментарии
Опубликовано 25 июля, 2010 – 14:37 пользователем daranton
Вот всё, что знаю…
Формула сферического зеркала − формула, связывающая параметры зеркала с расстоянием до него предмета и изображения:
1/F = 1/d + 1/f,
где: F − фокусное расстояние сферического зеркала;
d − расстояние от предмета до зеркала;
f − расстояние от изображения до зеркала.
Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.
Формула тонкой линзы аналогична формуле сферического зеркала.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 26 июля, 2010 – 12:07 пользователем daranton
А что, может Владимир Грабцевич добавить сюда в задачу…???
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 26 июля, 2010 – 14:28 пользователем В. Грабцевич
- Сделали бы к задаче рисунок.
- Решали бы через подобие треугольников, используя формулу:
1/F = 1/d + 1/f,
где F = R/2.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 26 июля, 2010 – 14:31 пользователем daranton
Не умею я рисунки делать…
Если помогли бы, то, может быть, ещё бы и освоил…???
Да и почему F = R/2 ?
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 26 июля, 2010 – 15:12 пользователем В. Грабцевич
- Учитесь пользоваться поиском, если хотите самостоятельно разобраться, как строится изображение в сферическом зеркале.
- Задача эта из известного сборника с решением.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 26 июля, 2010 – 22:00 пользователем В. Грабцевич
Укажите, из какого сборника Вы взяли решение, уважайте чужой труд. С какими данными получен ответ? При правильных способах решения задачи ответ должен быть одним. Уточните разные ответы.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 26 июля, 2010 – 23:39 пользователем daranton
Решение из учебника Драбовича К. Н., Макарова В. А., Чеснокова С. С. “Физика. Практический курс для поступающих в университеты”. 2006. Задача 4.1.23, страница 364.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 29 июля, 2010 – 15:35 пользователем daranton
А как бы Вы решили… можно Ваше решение именно через подобие треугольников…???
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 29 июля, 2010 – 15:55 пользователем В. Грабцевич
Например, смотрите рисунок из учебника выше, из подобия треугольников найдем длину тени на стене:
x/L = r/F,
x = (r/F) L,
прибавим d/2, получим радиус тени:
R = x + d/2 = (r/F) L + d/2,
откуда диаметр тени на экране:
D = 2R = 2 (r/F) L + d.
Это самое простое с использованием подобия треугольника.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 29 июля, 2010 – 16:24 пользователем daranton
Проверим, сходится ли ответ с учебником…
D = 2R = 2 (r/F) L + d.
D = 2 (0,01/0,4) 50 + 1 = 3,5 метра…
Ответ не сошёлся… Почему?
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 29 июля, 2010 – 16:47 пользователем daranton
D = 2lr/F + d,
D = 2R = 2 (r/F) L + d.
Одинаково, не правда ли???
А вот с данными запутался…
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 29 июля, 2010 – 19:51 пользователем В. Грабцевич
В книжном условии диаметр зеркала 10 см, а в Вашем условии 1 м, отсюда и разные ответы.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
-
-
March 8 2011, 20:38
- Дача
- Cancel
Определение длины тени: очень сложный и почти бесполезный способ
Эта идея посетила меня в процессе составления плана участка, когда я поняла, что хорошо бы более менее точно знать, какие его площади окажутся затененными и, главное, насколько. Выяснить это проще простого, нужно только набраться терпения и подождать еще пару месяцев до приезда в деревню. “Нет, нет, нет, нет, мы хотим сегодня!” Да, мы не ищем легких путей! И вот уже мозг отчаянно скрипит в попытках вспомнить школьный курс тригонометрии…
С детства есть у меня один “пунктик”: мне нравится иногда придумывать и решать всякие практические математические задачки. Не скажу, что часто этим занимаюсь. Но иногда это приносит даже некоторую пользу: например, недавно рассчитывала, сколько земли потребуется для большущего напольного горшка (для этого пришлось вычислять объем усеченного конуса).
А теперь вот занялась вычислением длины тени, получая удовольствие от самого процесса. Вряд ли этот метод кому-то пригодится в силу своей неоправданной сложности. Но результат я все-таки получила, и даже учла его при планировании, поэтому опишу этот способ, себе “на память”.
Необходимо вычислить длину тени фасадной стены дома.

Найти ВС можно по формуле:
ВС = АВ / tg<C,
где <C – высота Солнца , т.е. угол между направлением на Солнце и плоскостью горизонта.
Вычисляем длину тени, к примеру, для 15 апреля 2011 г.
Высота дома АВ = 4 м.
В астрономическом календаре находим значение высоты Солнца для 15 апреля 2011 г. В момент верхней кульминации <С = +43 гр. (для нулевого меридиана).
Вычисляем поправки: П = Д + Скл, где П – общая поправка, Д – поправка за долготу, Скл – поправка за склонение.
Д = N – L, где N – номер часового пояса, L – долгота пункта (в часах и минутах).
N = +3.
L = 34 58 ‘, переводим градусы в часы и минуты (1ч = 15 гр. долготы), получаем 2 20’
Д = 3 – 2 20 ‘ = 0 40 ‘
Скл = 0
Таким образом, с учетом поправки <С = +43 40 ‘
Вычисляем искомую длину тени:
ВС = 4 / tg <43 40 ‘
ВС = 4 / 0,9556
ВС = 4,2 м.
По такому же принципу я вычислила длину тени для восхода и захода (при этом учла, что в это время тень падает от боковых стен, высота которых меньше).
И для полного счастья на основе этих трех значений начертила примерный график “движения” тени по участку в течение дня.
Затем проделала ту же процедуру для других дней календаря (числа брала с интервалом в полмесяца).
Получилась вот такая таблица.
| Дата | Восход (длина тени от западной стены дома, м) | Верхняя кульминация (длина тени от северной стены дома, м) |
| 15.04 | 14,8 | 4,2 |
| 01.05 | 9,0 | 3,4 |
| 15.05 | 7,4 | 3,0 |
| 01.06 | 6,0 | 2,6 |
| 22.06 | 5,7 | 2,5 |
| 15.07 | 6,3 | 2,7 |
| 01.08 | 7,4 | 3,0 |
| 15.08 | 9,6 | 3,5 |