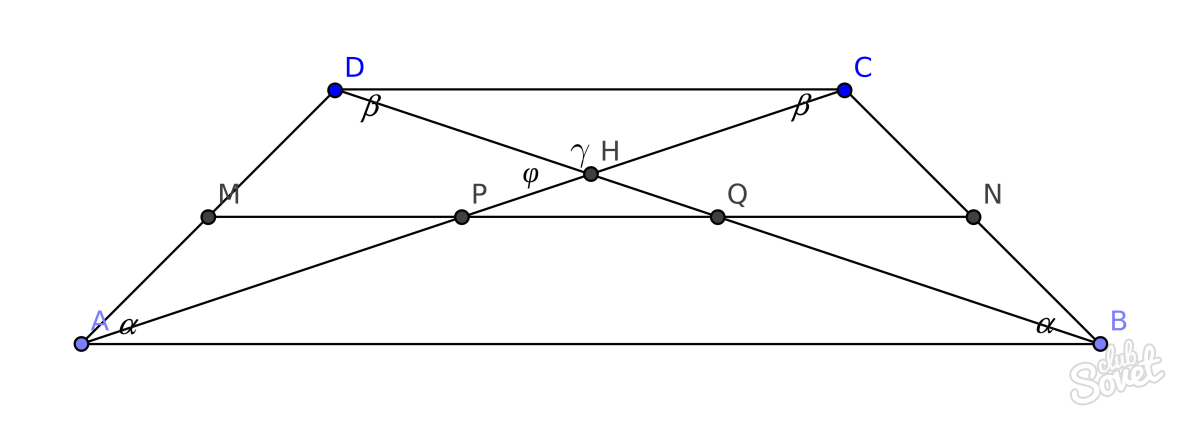
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
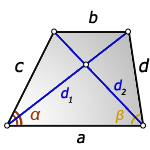
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
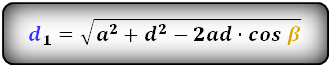
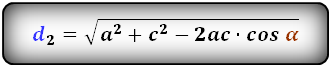
Формулы диагоналей трапеции через четыре стороны:
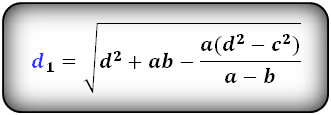

2. Формула длины диагоналей трапеции через высоту
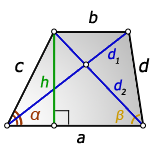
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
d1 , d2 – диагонали трапеции
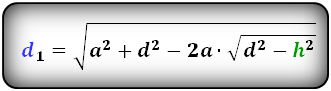
Формулы диагоналей трапеции через высоту:


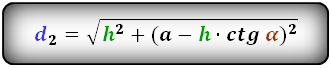


3. Формула длины диагонали трапеции через другую диагональ
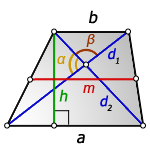
a – нижнее основание
b – верхнее основание
α, β – углы между диагоналями
h – высота трапеции
m – средняя линия трапеции
S – площадь трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции :
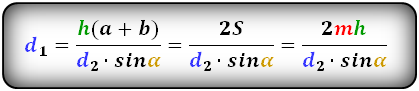
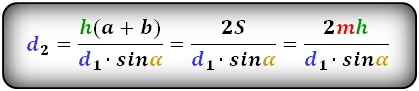
Справедливо для данного случая :
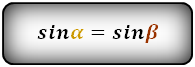
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
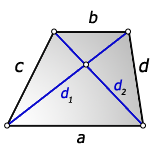
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
d1 , d2 – диагонали трапеции
Формула суммы квадратов диагоналей :
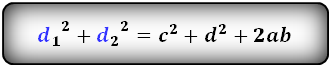
Формулы диагоналей трапеции :
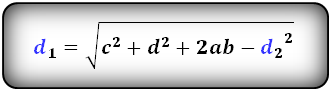
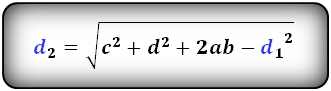
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 23 октября 2013
-
Обновлено: 13 августа 2021
Как найти периметр трапеции
Содержание:
- Основные свойства трапеции
-
Способы нахождений периметра
- По всем сторонам
- По сторонам равнобедренной трапеции
- Через среднюю линию
- Примеры решения задач
Определения
Трапеция — это четырехугольник, у которого лишь одна пара противолежащих сторон параллельна.
Периметр трапеции — это сумма длин всех его сторон.
Основные свойства трапеции
- средняя линия трапеции параллельна ее основаниям, а также равна половине их суммы;
- биссектриса любого угла данного четырехугольника отсекает на его основании отрезок, равный боковой стороне;
- треугольники ABO и DCO (на картинке), образованные диагоналями фигуры и ее основаниями, подобны;
- треугольники OAB и OCD, образованные диагоналями трапеции и ее боковыми сторонами, имеют одинаковую площадь;
- если сумма длин оснований четырехугольника равна сумме его боковых ребер, то в фигуру можно вписать окружность;
- точки M и N середины диагоналей лежат на одной прямой со средней линией фигуры. Также отрезок MN равен полуразность оснований четырехугольника;
- середины оснований фигуры, точка пересечения ее диагоналей, а также точка пересечения продолжений ее боковых сторон лежат на одной прямой;
Свойства равнобедренной трапеции
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- в равнобедренной трапеции углы при обоих ее основаниях одинаковы;
- диагонали равны;
- равнобедренную трапецию всегда можно вписать в окружность или описать окружность вокруг;
- если диагонали перпендикулярны, то высота фигуры равна полусумме ее оснований.
Способы нахождений периметра
Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.
По всем сторонам
Формула для нахождения периметра выглядит так:
P=a+b+c+d
где a, b, c, d — стороны трапеции.
По сторонам равнобедренной трапеции
Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:
(P=2times a+b+c)
или
(P=2times c+a+b)
Через среднюю линию
Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:
(P=2times l+AB+CD)
где l — средняя линия фигуры.
Примеры решения задач
Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.
Задача 1
Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.
Решение:
Нам пригодится самая первая формула для расчета:
P=a+b+c+d.
Подставляем значения и получаем:
P=4+7+5+10=26;см.
Ответ: 26 см.
Задача 2
Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.
Решение:
Так как трапеция равнобедренная, удобнее всего будет использовать формулу:
(P=2times a+b+c)
Таким образом, получается:
(P=2times 7+5+8=27) см.
Ответ: 27 см.
Задача 3
Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.
Решение:
Считать будем по формуле
(P=2times l+a+c)
(P=2times 6+5+9=26) см.
Ответ: 26 см.
Насколько полезной была для вас статья?
Рейтинг: 3.82 (Голосов: 11)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Диагональ выпуклого четырехугольника – это отрезок, соединяющий 2 противолежащие вершины. В
зависимости от типа геометрической фигуры диагональ обладает особыми свойствами, которые необходимо
знать и уметь применять на практике, так как большинство решений задач основывается именно на них. В
данной статье рассмотрены пути определения диагоналей, проведенных в трапеции.
Основные свойства фигуры и проведенных диагоналей способствуют выведению сокращенных формул, которые
помогут в решении задач по геометрии повышенного уровня. Рассмотрим несколько способов нахождения
искомого отрезка.
- Диагональ трапеции через нижнее основание, боковую сторону
и угол между ними - Диагональ трапеции через четыре стороны
- Диагональ трапеции через высоту, нижнее основание и угол
при нижнем основание - Диагональ трапеции через высоту, верхнее основание и угол
при нижнем основание - Диагональ трапеции через высоту, нижнее основание и боковую
сторону - Диагональ трапеции через высоту, основании и другую
известную диагональ - Диагональ трапеции через площадь и другую известную
диагональ - Диагональ трапеции через высоту, среднию линию и другую
известную диагональ - Диагональ равнобедренной трапеции через основании и боковую
сторону - Диагональ равнобедренной трапеции через высоту и среднию
линию - Диагональ равнобедренной трапеции через высоту и
основании - Диагональ равнобедренной трапеции через площадь и угол
между диагоналями - Диагональ прямоугольной трапеции через основание и
сторону - Диагональ прямоугольной трапеции через основание и
высоту
Вычисление через нижнее основание, боковую сторону и угол между ними
Зная длину стороны, большего основания трапеции и противолежащий по отношению к диагонали угол, можно
быстро найти результат благодаря формуле:
D = √(a² + b² — 2ac * cos β)
где c — сторона трапеции, a — основание, β – угол между ними.
Цифр после
запятой:
Результат в:
Пример. В трапеции проведена диагональ, противолежащий к ней острый угол равен 75
градусам. Прилежащие к данному углу основание и сторона трапеции равны 6,1 и 7 см. Найти проведенный
отрезок. D = √(6,1² + 7³ — 2 * 6,1 * 7 * cos75°) = 8 см – искомая
величина.
Вычисление через известные длины четырех сторон трапеции
Допустим, что a, b – основания, c и d – боковые стороны. Значение диагонали с учетом этих данных
легко можно найти, подставив их в формулу:
D =√(c² + ab — a * (c² — d²) / (a — b))
где a, b — основания, c, d — боковые стороны трапеции.
Цифр после
запятой:
Результат в:
Пример. Дана трапеция с боковыми сторонами 6 и 5 см, основаниями 4 и 8 см. Нужно
найти диагональ, которая лежит против угла. Применим данную формулу для решения: D = √(36 + 4 * 8 — 4(36 — 25) / (8 — 4)) = √(36 + 32 — 44 / 4) = 7,5 см
– неизвестная диагональ.
Вычисление через высоту, нижнее основание и угол при нижнем основании
Зная длину проведенной в трапеции высоты к нижнему основанию, значение которого также известно, и
один из двух углов при нижнем основании фигуры, можно найти диагональ, применив формулу:
D = √(h² + (a — h * ctg β)²)
где h — высота, a — нижнее основание, β – внутренний угол при основании.
Цифр после
запятой:
Результат в:
Пример. К нижнему основанию трапеции равному 7 м проведена высота, длина которой 8
м. Известен угол между нижним основанием и боковой стороной — 71°. Найти диагональ,
противолежащую известному углу. D = √(64 + (7 — 8 * ctg 71°)²) = 9 м
– длина искомого отрезка.
Вычисление через высоту, верхнее основание и угол при нижнем основании
В данном случае не нужно тратить время на поиски нижнего основания трапеции, стоит воспользоваться
формулой:
D = √(h² + (b + h * ctg α)²)
где b – длина верхнего основания трапеции.
Цифр после
запятой:
Результат в:
Пример. К нижнему основанию трапеции проведена высота длиной 6 мм. Длина верхнего
основания фигуры равна 4 мм, а внутренний угол — 71°. Найти: значение диагонали трапеции,
проходящей через вершину известного угла. D = √(36 + (4 + 6 * ctg 71°)²) = 8,5 мм.
Вычисление через высоту, нижнее основание и боковую сторону
Если известна длина одной из боковых сторон, нижнее основание и высота, проведенная к нему,
необходимо применить формулу:
D = √(a² + c² — 2a * √(c² — h²))
где a – нижнее основание трапеции, c – боковая сторона, h — высота.
Цифр после
запятой:
Результат в:
Пример. В трапеции проведена высота длиной 8 см к нижнему основанию длиной 7 см.
Известно, что одна из боковых сторон равна 9 см. Найти: диагональ, противолежащую острому углу между
нижним основанием и известной боковой стороной. D = √(49 + 81 — 14√81 — 64) = √(130 — 14√17) = √72,3 = 8,5 см
– искомая величина.
Вычисление через высоту, основании и другую известную диагональ
Кроме данных о высоте, верхнем и нижнем основании, одной из диагоналей, необходимо значить величину
углов, образующихся при пересечении диагоналей трапеции. Известно, что углы между отрезками
считаются смежными, а значит их синусы равны. Таким образом, подставляем все данные в формулу:
D = h(a+b) / d * sin α
где a, b – основания трапеции, α – острый или тупой угол между диагоналями, h — высота.
Цифр после
запятой:
Результат в:
Пример. Дана трапеция с основаниями 15 и 5 мм. Проведена высота длиной 10 мм, а
длина большей диагонали равна 20 мм. Найти: вторую диагональ, если известно, что угол при
пересечении отрезков равен 60°. D = 20(15 + 5) / 20 * sin 60° = 20 / sin 60° = 11,54 мм.
Вычисление через площадь трапеции и другую известную диагональ
Здесь также понадобится значение угла между данными отрезками. Способ нахождения через известную
площадь фигуры и другую диагональ имеет формулу вида:
D = 2S / d * sin α
где S – площадь, α – угол, d — известная диагональ
Цифр после
запятой:
Результат в:
Пример. Дана трапеция площадью 87 мм² с диагональю длиной 14,7 мм. Как найти
неизвестную диагональ, если угол между отрезками равен 65 градусам. D = 2 * 87 / 14,7 * sin 65° = 174 / 14,7 * sin 65° = 13 мм
– искомая величина.
Вычисление через высоту, среднюю линию и другую известную диагональ
Средняя линия трапеции – это отрезок, проходящий через середины боковых сторон данного
четырёхугольника. Через это значение искомая диагональ находится по формуле:
D = 2 * mh / d * sin α
где буквой m обозначается средняя линия трапеции, h — высота, d — известная
диагональ.
Цифр после
запятой:
Результат в:
Пример. Диагонали трапеции, одна из которых равна 19 мм, пересекаются под углом 65
градусов. Проведена средняя, длина которой 8 мм, а высота трапеции равна 15,5 мм. Найти: вторую
диагональ. D = 2 * 8 * 15,5 / 19 * sin 65° = 13 * sin 65° = 14,4 мм –
длина неизвестной диагонали.
Диагональ равнобедренной трапеции через основания и боковую сторону
Равнобедренная трапеция – часто встречающийся вид данного четырёхугольника. Основными признаками
равнобедренной фигуры служит равенство внутренних углов при основании, а также равенство диагоналей.
Найти диагональ, проведенную в равнобедренной трапеции, можно несколькими способами. К примеру,
вычислить искомую величину можно по формуле:
D = √(c² + a * b)
где c – известная боковая сторона, a и b – верхнее и нижнее основание трапеции.
Цифр после
запятой:
Результат в:
Пример. Углы трапеции при основаниях, равных 8 и 18 см, имеют одинаковую градусную
меру. Одна из боковых сторон равна 6 см. Найти: диагональ. Из равенства углов делаем вывод, что дана
равнобедренная трапеция. Затем подставляем известные значения в формулу: D = √(36 + 8 * 18) = √180 = 13,4 см
– длина диагоналей равнобедренной трапеции.
Диагональ равнобедренной трапеции через высоту и среднюю линию
Зная длину высоты и отрезок, проходящий через середины сторон равнобедренной трапеции, можно легко
найти искомую величину по формуле:
D = √(h² + m²)
где буквой m обозначена средняя линия, а h — высота.
Цифр после
запятой:
Результат в:
Пример. В трапеции проведена высота длиной 7 м, диагонали равны. Как найти
диагонали, если известна длина средней линии – 9 м? Из равенства диагоналей можно сделать вывод, что
трапеция равнобедренная. А значит, что для быстрого решения нужно воспользоваться выше указанной
формулой: D = √(7² + 9²) = √(49+81) = √130 = 14,4 м – диагонали трапеции.
Диагональ равнобедренной трапеции через высоту, верхнее и нижнее основание
Формула нахождения искомого отрезка при помощи высоты и известных величин оснований имеет следующий
вид:
D = √(h² + (a² + b²) / 4)
где a и b – верхнее и нижнее основание равнобедренной трапеции, h — высота.
Цифр после
запятой:
Результат в:
Пример. Дана равнобедренная трапеция, в которой к нижнему основанию проведена высота
длиной 7 см. Основания – 5 и 11 см. Найти: диагонали. D = √(7² +(5² + 11²) / 4) = √(49 + 146 / 4) = √85,5 = 10,6 см
– длина диагоналей.
Диагональ равнобедренной трапеции через площадь и угол между диагоналями
Как уже говорилось, синусы углов, образованных пересечением диагоналей, равны, так как углы являются
смежными. Поэтому для вычисления по следующей формуле, необходим любой из этих углов. Формула:
D = √2*S / sin α
где S — площадь, sin α — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Дана равнобедренная трапеция, площадь которой равна 86 мм². Найти: длину
диагоналей, один из углов при пересечении которых равен 120 градусам. D = √(2 * 86 / sin 120°) = √(172 / sin 120°) = 14 мм.
Диагональ прямоугольной трапеции через основание и сторону
В прямоугольной трапеции одна из боковых сторон расположена перпендикулярно основаниям (под углом
90°). Зная одно из оснований такого четырёхугольника и боковую сторону, можно легко найти диагональ,
применив следующую формулу:
D = √(a² + c²)
где a – основание, c — сторона.
Цифр после
запятой:
Результат в:
Пример. Внутренний угол трапеции между боковой стороной и основаниями равен 90
градусам. Сторона равна 20 м, нижнее основание – 15 м. Найти: диагональ трапеции, противолежащую
прямому углу. Исходя их известных данных, делаем вывод, что дана прямоугольная трапеция. Затем
подставляем значения в формулу: D = √(20²+15²) = 25 м. Аналогичный способ
решения можно применить для того случая, когда известна длина верхнего основания.
Диагональ прямоугольной трапеции через основание и высоту
В данном случае высота равна боковой стороне, перпендикулярной основанию, поэтому вместо стороны в
формулу просто подставляется значение высоты при необходимости:
D = √(a² + h²)
где a — основание, h — высота.
Цифр после
запятой:
Результат в:
Пример. Дана прямоугольная трапеция с высотой равной 15 см и основанием — 10
см. Найти: диагональ. D = √(15² + 10²) = 18 см.
Трапеция – выпуклая плоская геометрическая фигура, которая представляет собой четырёхугольник.
Обязательным условием данного вида является параллельность двух сторон (они называются основаниями).
Как и упоминалось выше, в зависимости от боковых сторон трапеция может быть равнобедренной и
прямоугольной.
Рассмотрим некоторые свойства четырёхугольника, знание которых необходимо для решения самых
простейших задач:
- В трапецию можно вписать окружность, если сумма оснований равна сумме боковых сторон.
- Средняя линия параллельна основаниям, M=(a+b)/2, где a и b – основания.
- На одной прямой лежат точки пересечения диагоналей и продолжения длин боковых сторон.
Диагональ, построенная в данной фигуре, отличается следующими свойствами:
- Диагонали разделяют фигуру на 2 подобных треугольника, углы которых равны, а стороны
пропорциональны. - Проведенные диагонали также образуют 2 идентичных треугольника, стороны которых совпадают со
сторонами трапеции. - Отрезок, проходящий через точку пересечения диагоналей и соединяющий основания фигуры, делится в
пропорции, равной соотношению оснований фигуры. - Отрезок, проходящий через середины диагоналей, делит боковые стороны трапеции на 2 равные
части.
В решении задач значение диагонали поможет определить немалое количество нужных величин: высота,
площадь, периметр, все стороны и среднюю линию трапеции, внутренние углы. Хорошие навыки применения
тригонометрических функций способствуют быстрой скорости решения по данных формулам, которые
значительно облегчают и ускоряют процесс.
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции – параллельные стороны
- Боковые стороны – две другие стороны
- Средняя линия – отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция – трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m – b
b = 2m – a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Определение.
Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 – 2ad·cos β
d2 = √a2 + c2 – 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab – | a(d 2 – c2) |
| a – b |
| d2 = | √ | c2 + ab – | a(c2 – d 2) |
| a – b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a – h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a – h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab – d22
d2 = √c2 + d 2 + 2ab – d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 – | ( | (a – b)2 + c2 – d 2 | ) | 2 |
| 2 | 2(a – b) |
5. Формула Герона для трапеции
| S = | a + b | √(p – a)(p – b)(p – a – c)(p – a – d) |
| |a – b| |
где
| p = | a + b + c + d | – полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p – a)(p – c)(p – d1) |
где
a – большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Как найти диагональ трапеции
Знакомство с трапецией впервые происходит при изучении курса планиметрии. Хотя и до этого вы наверняка встречали предметы, форма которых совпадает с данной геометрической фигурой. Четырехугольник отличается тем, что только 2 из его четырех сторон параллельны. Если соединить противолежащие вершины фигуры отрезками, то получим ее диагонали. Как определить их длину? Величина этих отрезков связана с углами фигуры, длиной ее сторон и высоты.
1
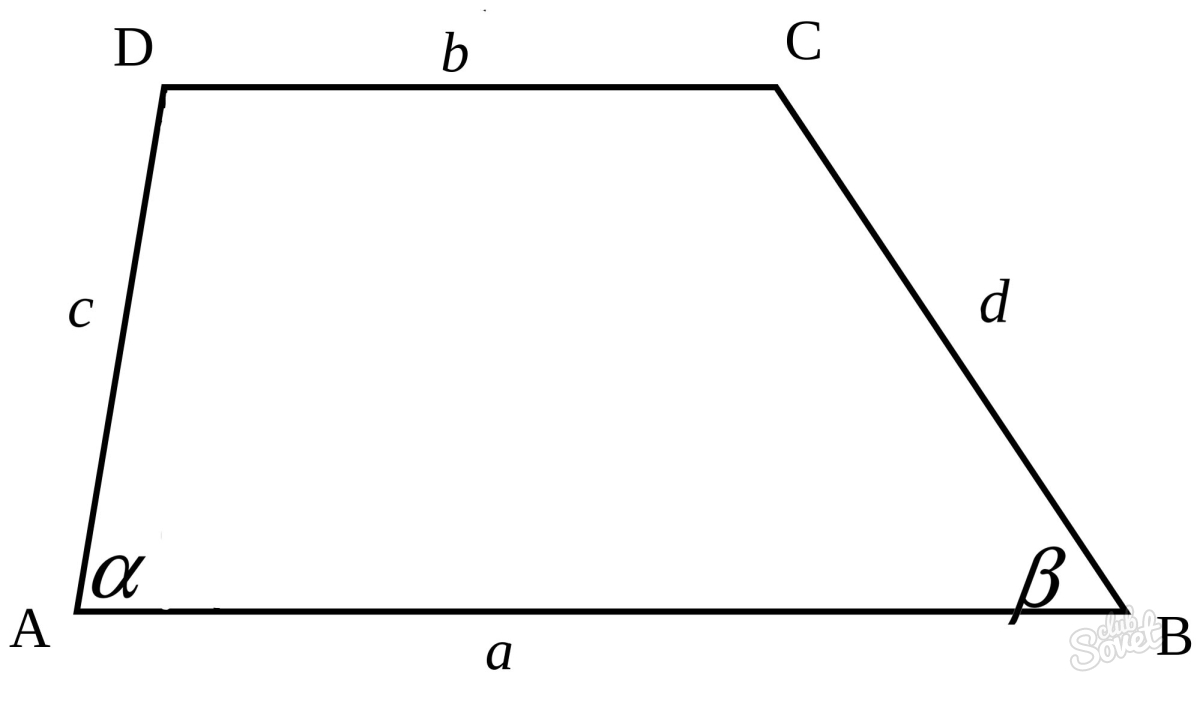
Диагонали и углы трапеции
Если перед вами произвольная трапеция с известными углами в основании, а также боковыми сторонами и основанием, то в определении величины диагоналей поможет следующее соотношение:
d1 = √a2 + d2 – 2ad*cosβ,
d2 = √a2 + c2 – 2ac*cosα,
d1, d2 – искомые диагонали,
a – основание,
c, d – боковые стороны,
β, α – углы, лежащие в основании.
В его основе лежит теорема косинусов, позволяющая в треугольнике определить длину стороны, используя известные величины двух других сторон, а также угла, лежащего против искомой стороны.
2
Диагонали и стороны трапеции
- При наличии известных всех четырех сторон фигуры для нахождения ее диагоналей можно использовать выражения:
d1 = √ d2 + ab – (a(d2 – c2)/(a-b)),
d2 = √ c2 + ab – (a(c2 – d2)/(a-b)).
- Взаимосвязь между диагоналями:
d12 + d22 = c2 + d2 + 2ab,
d1 = √c2 + d2 + 2ab – d22,
d2 = √c2 + d2 + 2ab – d12,
Как в первом, так и во втором случаях:
d1, d2 – искомые диагонали,
a, b – основания,
c, d – боковые стороны.

3
Диагонали и высота трапеции
При известном значении одного из оснований фигуры или боковой стороны, угла при нижнем основании, а также высоты четырехугольника, с определением длин диагоналей также не возникнет сложностей.
d1 = √h2 + (a – h*ctgβ)2,
d1 = √h2 + (b + h*ctgα)2,
d1 = √a2 + d2 – 2a √d2 – h2,
d1 = √h2 + (a – h*ctgα)2,
d1 = √h2 + (b + h*ctgβ)2,
d1 = √a2 + c2 – 2a √c2 – h2,
d1, d2 – искомые диагонали,
a, b – основания,
β, α – углы, лежащие в основании.
c, d – боковые стороны,
h – высота фигуры.

4
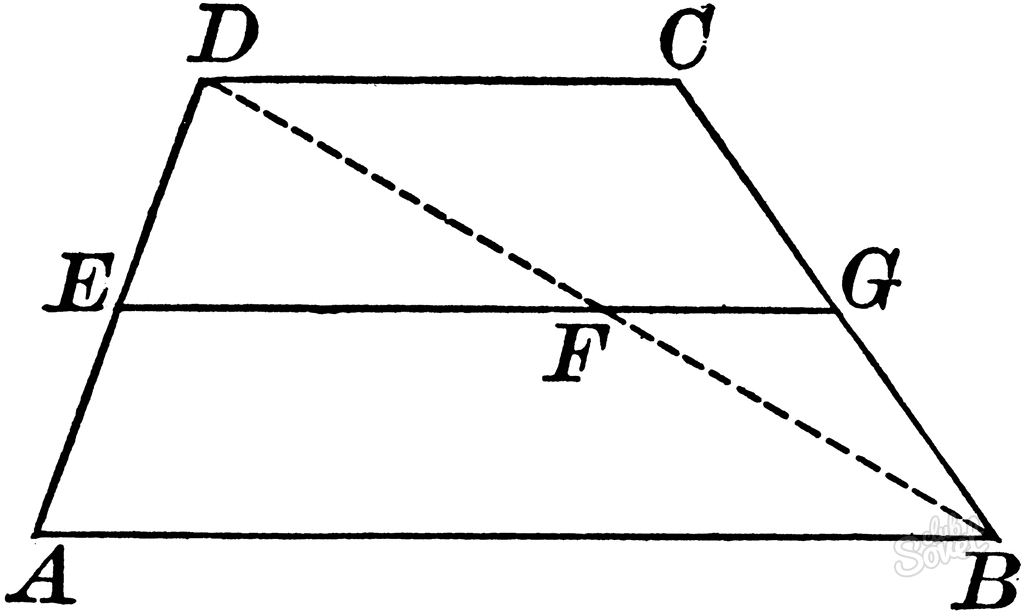
Диагонали и средняя линия трапеции
Если в числе заданных величин присутствует средняя линия, то с ее помощью также можно вычислить длину диагоналей фигуры. Соотношение верно лишь в случаях, когда sinφ = sin γ.
Т.к. l = d1*d2*sinφ/2h = d1*d2*sin γ/2h,
d1 = 2hl/ d2*sinφ = 2hl/ d2*sin γ,
d2 = 2hl/ d1*sinφ = 2hl/ d1*sin γ,
d1, d2 – искомые диагонали,
φ, γ – углы между ними,
h – высота фигуры,
l – ее средняя линия.
5
Фигура равнобокая
Если по условиям задания трапеция имеет равные боковые стороны, то выражения для нахождения диагоналей фигуры преобразуются с учетом того, что c=d:
d1 = d2 = √c2 + ab,
d1 = d2 = √a2 + c2 – 2ac*cosα,
d1 = d2 = √a2 + c2 + 2ac*cosβ,
d1 = d2 = √b2 + c2 – 2bc*cosβ,
d1 = d2 = √b2 + c2 + 2bc*cosα,
d1 = d2 = √h2 + l2,
d1 = d2 = √h2 + (a+b)2/4,
d1 = d2 = √h*(a+b)/sinφ = √2S/ sinφ = √2lh/sinφ (sinφ = sin γ),
d1, d2 – искомые диагонали,
φ, γ – углы между ними,
h – высота фигуры,
S – площадь,
a, b – основания (a < b),
c – боковая сторона,
l – средняя линия.