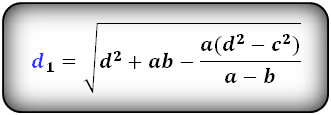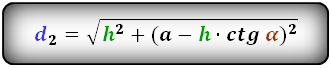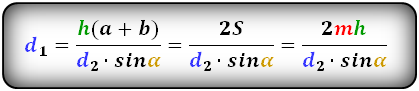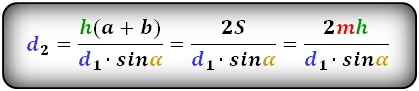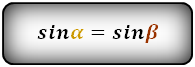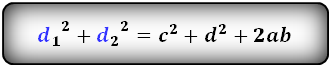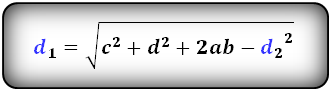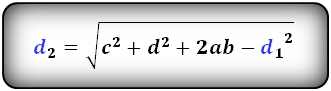Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
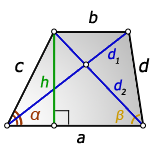
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
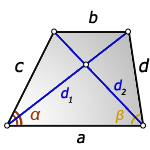
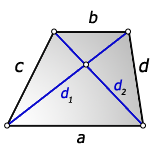
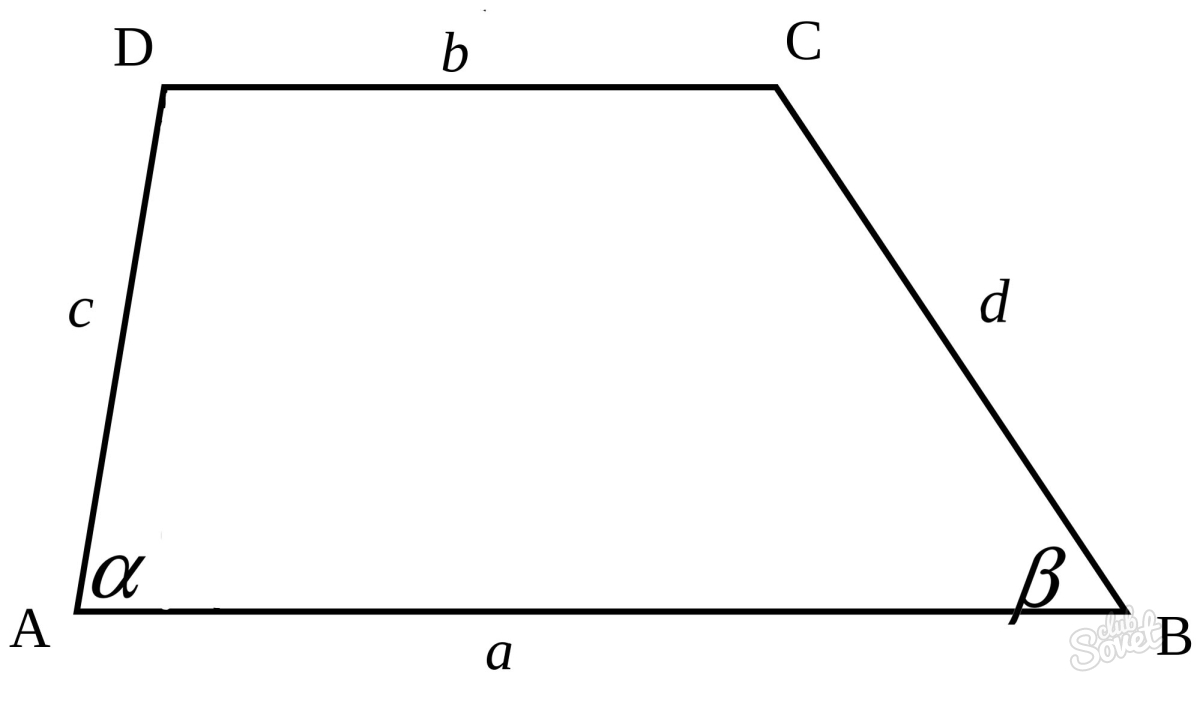
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
d1 , d2 – диагонали трапеции
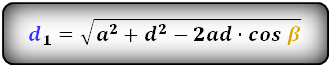
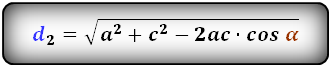
Формулы диагоналей трапеции по теореме косинусов:
Формулы диагоналей трапеции через четыре стороны:
2. Формула длины диагоналей трапеции через высоту
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции через высоту:
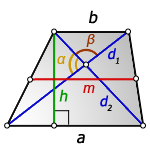
3. Формула длины диагонали трапеции через другую диагональ
a – нижнее основание
b – верхнее основание
α, β – углы между диагоналями
h – высота трапеции
m – средняя линия трапеции
S – площадь трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции :
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
d1 , d2 – диагонали трапеции
Формула суммы квадратов диагоналей :
Формулы диагоналей трапеции :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 23 октября 2013
-
Обновлено: 13 августа 2021
Диагональ выпуклого четырехугольника – это отрезок, соединяющий 2 противолежащие вершины. В
зависимости от типа геометрической фигуры диагональ обладает особыми свойствами, которые необходимо
знать и уметь применять на практике, так как большинство решений задач основывается именно на них. В
данной статье рассмотрены пути определения диагоналей, проведенных в трапеции.
Основные свойства фигуры и проведенных диагоналей способствуют выведению сокращенных формул, которые
помогут в решении задач по геометрии повышенного уровня. Рассмотрим несколько способов нахождения
искомого отрезка.
- Диагональ трапеции через нижнее основание, боковую сторону
и угол между ними - Диагональ трапеции через четыре стороны
- Диагональ трапеции через высоту, нижнее основание и угол
при нижнем основание - Диагональ трапеции через высоту, верхнее основание и угол
при нижнем основание - Диагональ трапеции через высоту, нижнее основание и боковую
сторону - Диагональ трапеции через высоту, основании и другую
известную диагональ - Диагональ трапеции через площадь и другую известную
диагональ - Диагональ трапеции через высоту, среднию линию и другую
известную диагональ - Диагональ равнобедренной трапеции через основании и боковую
сторону - Диагональ равнобедренной трапеции через высоту и среднию
линию - Диагональ равнобедренной трапеции через высоту и
основании - Диагональ равнобедренной трапеции через площадь и угол
между диагоналями - Диагональ прямоугольной трапеции через основание и
сторону - Диагональ прямоугольной трапеции через основание и
высоту
Вычисление через нижнее основание, боковую сторону и угол между ними
Зная длину стороны, большего основания трапеции и противолежащий по отношению к диагонали угол, можно
быстро найти результат благодаря формуле:
D = √(a² + b² — 2ac * cos β)
где c — сторона трапеции, a — основание, β – угол между ними.
Цифр после
запятой:
Результат в:
Пример. В трапеции проведена диагональ, противолежащий к ней острый угол равен 75
градусам. Прилежащие к данному углу основание и сторона трапеции равны 6,1 и 7 см. Найти проведенный
отрезок. D = √(6,1² + 7³ — 2 * 6,1 * 7 * cos75°) = 8 см – искомая
величина.
Вычисление через известные длины четырех сторон трапеции
Допустим, что a, b – основания, c и d – боковые стороны. Значение диагонали с учетом этих данных
легко можно найти, подставив их в формулу:
D =√(c² + ab — a * (c² — d²) / (a — b))
где a, b — основания, c, d — боковые стороны трапеции.
Цифр после
запятой:
Результат в:
Пример. Дана трапеция с боковыми сторонами 6 и 5 см, основаниями 4 и 8 см. Нужно
найти диагональ, которая лежит против угла. Применим данную формулу для решения: D = √(36 + 4 * 8 — 4(36 — 25) / (8 — 4)) = √(36 + 32 — 44 / 4) = 7,5 см
– неизвестная диагональ.
Вычисление через высоту, нижнее основание и угол при нижнем основании
Зная длину проведенной в трапеции высоты к нижнему основанию, значение которого также известно, и
один из двух углов при нижнем основании фигуры, можно найти диагональ, применив формулу:
D = √(h² + (a — h * ctg β)²)
где h — высота, a — нижнее основание, β – внутренний угол при основании.
Цифр после
запятой:
Результат в:
Пример. К нижнему основанию трапеции равному 7 м проведена высота, длина которой 8
м. Известен угол между нижним основанием и боковой стороной — 71°. Найти диагональ,
противолежащую известному углу. D = √(64 + (7 — 8 * ctg 71°)²) = 9 м
– длина искомого отрезка.
Вычисление через высоту, верхнее основание и угол при нижнем основании
В данном случае не нужно тратить время на поиски нижнего основания трапеции, стоит воспользоваться
формулой:
D = √(h² + (b + h * ctg α)²)
где b – длина верхнего основания трапеции.
Цифр после
запятой:
Результат в:
Пример. К нижнему основанию трапеции проведена высота длиной 6 мм. Длина верхнего
основания фигуры равна 4 мм, а внутренний угол — 71°. Найти: значение диагонали трапеции,
проходящей через вершину известного угла. D = √(36 + (4 + 6 * ctg 71°)²) = 8,5 мм.
Вычисление через высоту, нижнее основание и боковую сторону
Если известна длина одной из боковых сторон, нижнее основание и высота, проведенная к нему,
необходимо применить формулу:
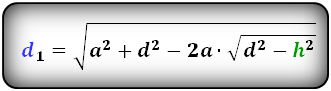
D = √(a² + c² — 2a * √(c² — h²))
где a – нижнее основание трапеции, c – боковая сторона, h — высота.
Цифр после
запятой:
Результат в:
Пример. В трапеции проведена высота длиной 8 см к нижнему основанию длиной 7 см.
Известно, что одна из боковых сторон равна 9 см. Найти: диагональ, противолежащую острому углу между
нижним основанием и известной боковой стороной. D = √(49 + 81 — 14√81 — 64) = √(130 — 14√17) = √72,3 = 8,5 см
– искомая величина.
Вычисление через высоту, основании и другую известную диагональ
Кроме данных о высоте, верхнем и нижнем основании, одной из диагоналей, необходимо значить величину
углов, образующихся при пересечении диагоналей трапеции. Известно, что углы между отрезками
считаются смежными, а значит их синусы равны. Таким образом, подставляем все данные в формулу:
D = h(a+b) / d * sin α
где a, b – основания трапеции, α – острый или тупой угол между диагоналями, h — высота.
Цифр после
запятой:
Результат в:
Пример. Дана трапеция с основаниями 15 и 5 мм. Проведена высота длиной 10 мм, а
длина большей диагонали равна 20 мм. Найти: вторую диагональ, если известно, что угол при
пересечении отрезков равен 60°. D = 20(15 + 5) / 20 * sin 60° = 20 / sin 60° = 11,54 мм.
Вычисление через площадь трапеции и другую известную диагональ
Здесь также понадобится значение угла между данными отрезками. Способ нахождения через известную
площадь фигуры и другую диагональ имеет формулу вида:
D = 2S / d * sin α
где S – площадь, α – угол, d — известная диагональ
Цифр после
запятой:
Результат в:
Пример. Дана трапеция площадью 87 мм² с диагональю длиной 14,7 мм. Как найти
неизвестную диагональ, если угол между отрезками равен 65 градусам. D = 2 * 87 / 14,7 * sin 65° = 174 / 14,7 * sin 65° = 13 мм
– искомая величина.
Вычисление через высоту, среднюю линию и другую известную диагональ
Средняя линия трапеции – это отрезок, проходящий через середины боковых сторон данного
четырёхугольника. Через это значение искомая диагональ находится по формуле:
D = 2 * mh / d * sin α
где буквой m обозначается средняя линия трапеции, h — высота, d — известная
диагональ.
Цифр после
запятой:
Результат в:
Пример. Диагонали трапеции, одна из которых равна 19 мм, пересекаются под углом 65
градусов. Проведена средняя, длина которой 8 мм, а высота трапеции равна 15,5 мм. Найти: вторую
диагональ. D = 2 * 8 * 15,5 / 19 * sin 65° = 13 * sin 65° = 14,4 мм –
длина неизвестной диагонали.
Диагональ равнобедренной трапеции через основания и боковую сторону
Равнобедренная трапеция – часто встречающийся вид данного четырёхугольника. Основными признаками
равнобедренной фигуры служит равенство внутренних углов при основании, а также равенство диагоналей.
Найти диагональ, проведенную в равнобедренной трапеции, можно несколькими способами. К примеру,
вычислить искомую величину можно по формуле:
D = √(c² + a * b)
где c – известная боковая сторона, a и b – верхнее и нижнее основание трапеции.
Цифр после
запятой:
Результат в:
Пример. Углы трапеции при основаниях, равных 8 и 18 см, имеют одинаковую градусную
меру. Одна из боковых сторон равна 6 см. Найти: диагональ. Из равенства углов делаем вывод, что дана
равнобедренная трапеция. Затем подставляем известные значения в формулу: D = √(36 + 8 * 18) = √180 = 13,4 см
– длина диагоналей равнобедренной трапеции.
Диагональ равнобедренной трапеции через высоту и среднюю линию
Зная длину высоты и отрезок, проходящий через середины сторон равнобедренной трапеции, можно легко
найти искомую величину по формуле:
D = √(h² + m²)
где буквой m обозначена средняя линия, а h — высота.
Цифр после
запятой:
Результат в:
Пример. В трапеции проведена высота длиной 7 м, диагонали равны. Как найти
диагонали, если известна длина средней линии – 9 м? Из равенства диагоналей можно сделать вывод, что
трапеция равнобедренная. А значит, что для быстрого решения нужно воспользоваться выше указанной
формулой: D = √(7² + 9²) = √(49+81) = √130 = 14,4 м – диагонали трапеции.
Диагональ равнобедренной трапеции через высоту, верхнее и нижнее основание
Формула нахождения искомого отрезка при помощи высоты и известных величин оснований имеет следующий
вид:
D = √(h² + (a² + b²) / 4)
где a и b – верхнее и нижнее основание равнобедренной трапеции, h — высота.
Цифр после
запятой:
Результат в:
Пример. Дана равнобедренная трапеция, в которой к нижнему основанию проведена высота
длиной 7 см. Основания – 5 и 11 см. Найти: диагонали. D = √(7² +(5² + 11²) / 4) = √(49 + 146 / 4) = √85,5 = 10,6 см
– длина диагоналей.
Диагональ равнобедренной трапеции через площадь и угол между диагоналями
Как уже говорилось, синусы углов, образованных пересечением диагоналей, равны, так как углы являются
смежными. Поэтому для вычисления по следующей формуле, необходим любой из этих углов. Формула:
D = √2*S / sin α
где S — площадь, sin α — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Дана равнобедренная трапеция, площадь которой равна 86 мм². Найти: длину
диагоналей, один из углов при пересечении которых равен 120 градусам. D = √(2 * 86 / sin 120°) = √(172 / sin 120°) = 14 мм.
Диагональ прямоугольной трапеции через основание и сторону
В прямоугольной трапеции одна из боковых сторон расположена перпендикулярно основаниям (под углом
90°). Зная одно из оснований такого четырёхугольника и боковую сторону, можно легко найти диагональ,
применив следующую формулу:
D = √(a² + c²)
где a – основание, c — сторона.
Цифр после
запятой:
Результат в:
Пример. Внутренний угол трапеции между боковой стороной и основаниями равен 90
градусам. Сторона равна 20 м, нижнее основание – 15 м. Найти: диагональ трапеции, противолежащую
прямому углу. Исходя их известных данных, делаем вывод, что дана прямоугольная трапеция. Затем
подставляем значения в формулу: D = √(20²+15²) = 25 м. Аналогичный способ
решения можно применить для того случая, когда известна длина верхнего основания.
Диагональ прямоугольной трапеции через основание и высоту
В данном случае высота равна боковой стороне, перпендикулярной основанию, поэтому вместо стороны в
формулу просто подставляется значение высоты при необходимости:
D = √(a² + h²)
где a — основание, h — высота.
Цифр после
запятой:
Результат в:
Пример. Дана прямоугольная трапеция с высотой равной 15 см и основанием — 10
см. Найти: диагональ. D = √(15² + 10²) = 18 см.
Трапеция – выпуклая плоская геометрическая фигура, которая представляет собой четырёхугольник.
Обязательным условием данного вида является параллельность двух сторон (они называются основаниями).
Как и упоминалось выше, в зависимости от боковых сторон трапеция может быть равнобедренной и
прямоугольной.
Рассмотрим некоторые свойства четырёхугольника, знание которых необходимо для решения самых
простейших задач:
- В трапецию можно вписать окружность, если сумма оснований равна сумме боковых сторон.
- Средняя линия параллельна основаниям, M=(a+b)/2, где a и b – основания.
- На одной прямой лежат точки пересечения диагоналей и продолжения длин боковых сторон.
Диагональ, построенная в данной фигуре, отличается следующими свойствами:
- Диагонали разделяют фигуру на 2 подобных треугольника, углы которых равны, а стороны
пропорциональны. - Проведенные диагонали также образуют 2 идентичных треугольника, стороны которых совпадают со
сторонами трапеции. - Отрезок, проходящий через точку пересечения диагоналей и соединяющий основания фигуры, делится в
пропорции, равной соотношению оснований фигуры. - Отрезок, проходящий через середины диагоналей, делит боковые стороны трапеции на 2 равные
части.
В решении задач значение диагонали поможет определить немалое количество нужных величин: высота,
площадь, периметр, все стороны и среднюю линию трапеции, внутренние углы. Хорошие навыки применения
тригонометрических функций способствуют быстрой скорости решения по данных формулам, которые
значительно облегчают и ускоряют процесс.
Как найти диагональ равнобедренной трапеции
Трапеция, в которой длины боковых сторон равны, а основания параллельны, называется равнобедренной или равнобокой. Обе диагонали в такой геометрической фигуре имеют одинаковую длину, которую в зависимости от известных параметров трапеции можно рассчитать разными способами.
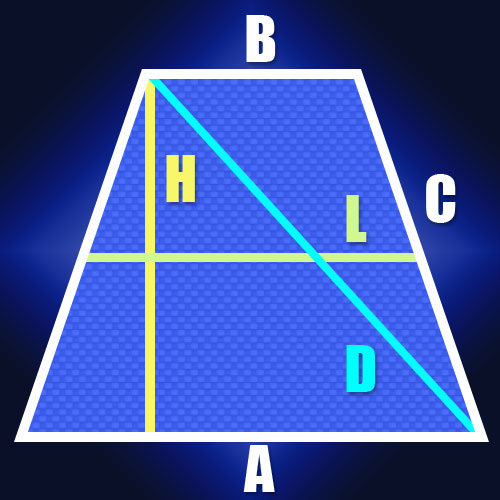
Инструкция
Если известны длины оснований равнобедренной трапеции (A и B) и длина ее боковой стороны (C), то для определения длин диагоналей (D) можно воспользоваться тем, что сумма квадратов длин всех сторон равна сумме квадратов длин диагоналей. Это свойство вытекает из того факта, что каждая из диагоналей трапеции является гипотенузой треугольника, катетами в котором служат боковая сторона и основание. А согласно теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы. Так как боковые стороны в равнобедренной трапеции равны, как и ее диагонали, то это свойство можно записать в таком виде: A² + B² + 2C² = 2D². Из этой формулы вытекает, что длина диагонали равна квадратному корню из половины суммы квадратов длин оснований, сложенной с квадратом длины боковой стороны: D = √((A² + B²)/2 + C²).
Если длины сторон не известны, но есть длина средней линии (L) и высота (H) равнобедренной трапеции, то длину диагонали (D) тоже вычислить несложно. Так как длина средней линии равна полусумме оснований трапеции, то это дает возможность найти длину отрезка между точкой на большем основании, в которую опущена высота, и вершиной, прилегающей к этому основанию. В равнобедренной трапеции длина этого отрезка будет совпадать с длиной средней линии. Так как диагональ замыкает этот отрезок и высоту трапеции в прямоугольный треугольник, то вычислить ее длину не составит труда. Например, по той же самой теореме Пифагора она будет равна квадратному корню из суммы квадратов высоты и средней линии: D=√(L² + H²).
Если известны длины обоих оснований равнобедренной трапеции (A и B) и ее высота (H), то, как и в предыдущем случае, можно вычислить длину отрезка между точкой, опущенной на большую сторону высоты и прилегающей к ней вершиной. Формула из предыдущего шага трансформируется к такому виду: D=√((A + B)²/4 + H²).
Источники:
- диагональ в равнобедренной трапеции
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти диагональ трапеции
Знакомство с трапецией впервые происходит при изучении курса планиметрии. Хотя и до этого вы наверняка встречали предметы, форма которых совпадает с данной геометрической фигурой. Четырехугольник отличается тем, что только 2 из его четырех сторон параллельны. Если соединить противолежащие вершины фигуры отрезками, то получим ее диагонали. Как определить их длину? Величина этих отрезков связана с углами фигуры, длиной ее сторон и высоты.
1
Диагонали и углы трапеции
Если перед вами произвольная трапеция с известными углами в основании, а также боковыми сторонами и основанием, то в определении величины диагоналей поможет следующее соотношение:
d1 = √a2 + d2 – 2ad*cosβ,
d2 = √a2 + c2 – 2ac*cosα,
d1, d2 – искомые диагонали,
a – основание,
c, d – боковые стороны,
β, α – углы, лежащие в основании.
В его основе лежит теорема косинусов, позволяющая в треугольнике определить длину стороны, используя известные величины двух других сторон, а также угла, лежащего против искомой стороны.
2
Диагонали и стороны трапеции
- При наличии известных всех четырех сторон фигуры для нахождения ее диагоналей можно использовать выражения:
d1 = √ d2 + ab – (a(d2 – c2)/(a-b)),
d2 = √ c2 + ab – (a(c2 – d2)/(a-b)).
- Взаимосвязь между диагоналями:
d12 + d22 = c2 + d2 + 2ab,
d1 = √c2 + d2 + 2ab – d22,
d2 = √c2 + d2 + 2ab – d12,
Как в первом, так и во втором случаях:
d1, d2 – искомые диагонали,
a, b – основания,
c, d – боковые стороны.
3
Диагонали и высота трапеции
При известном значении одного из оснований фигуры или боковой стороны, угла при нижнем основании, а также высоты четырехугольника, с определением длин диагоналей также не возникнет сложностей.
d1 = √h2 + (a – h*ctgβ)2,
d1 = √h2 + (b + h*ctgα)2,
d1 = √a2 + d2 – 2a √d2 – h2,
d1 = √h2 + (a – h*ctgα)2,
d1 = √h2 + (b + h*ctgβ)2,
d1 = √a2 + c2 – 2a √c2 – h2,
d1, d2 – искомые диагонали,
a, b – основания,
β, α – углы, лежащие в основании.
c, d – боковые стороны,
h – высота фигуры.
4
Диагонали и средняя линия трапеции
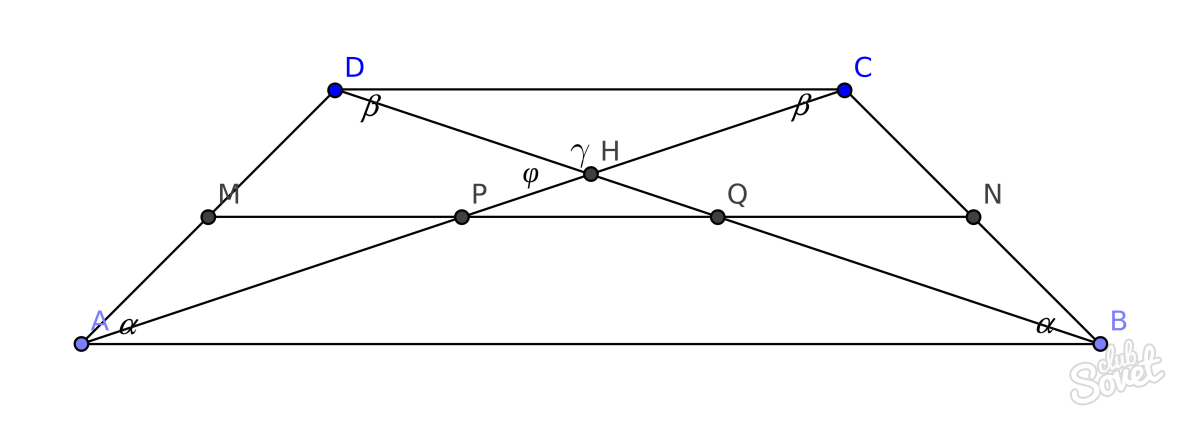
Если в числе заданных величин присутствует средняя линия, то с ее помощью также можно вычислить длину диагоналей фигуры. Соотношение верно лишь в случаях, когда sinφ = sin γ.
Т.к. l = d1*d2*sinφ/2h = d1*d2*sin γ/2h,
d1 = 2hl/ d2*sinφ = 2hl/ d2*sin γ,
d2 = 2hl/ d1*sinφ = 2hl/ d1*sin γ,
d1, d2 – искомые диагонали,
φ, γ – углы между ними,
h – высота фигуры,
l – ее средняя линия.
5
Фигура равнобокая
Если по условиям задания трапеция имеет равные боковые стороны, то выражения для нахождения диагоналей фигуры преобразуются с учетом того, что c=d:
d1 = d2 = √c2 + ab,
d1 = d2 = √a2 + c2 – 2ac*cosα,
d1 = d2 = √a2 + c2 + 2ac*cosβ,
d1 = d2 = √b2 + c2 – 2bc*cosβ,
d1 = d2 = √b2 + c2 + 2bc*cosα,
d1 = d2 = √h2 + l2,
d1 = d2 = √h2 + (a+b)2/4,
d1 = d2 = √h*(a+b)/sinφ = √2S/ sinφ = √2lh/sinφ (sinφ = sin γ),
d1, d2 – искомые диагонали,
φ, γ – углы между ними,
h – высота фигуры,
S – площадь,
a, b – основания (a < b),
c – боковая сторона,
l – средняя линия.
Найти диагональ трапеции можно несколькими способами. В основе первого способа лежит теорема косинусов в треугольнике, который получается внутри трапеции при проведении диагонали. Если известны одно из оснований трапеции и прилежащая к нему боковая сторона, а также угол между ними, то формула диагонали будет такая же, как и для параллелограмма:
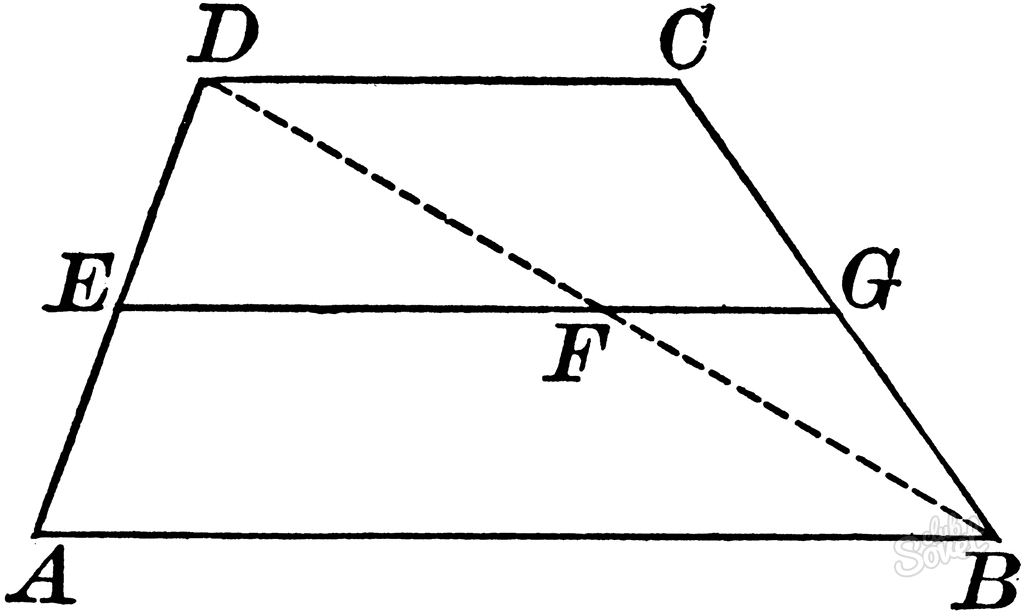
Можно вычислить диагональ трапеции через стороны. Для этого необходимо знать все четыре стороны. Выведение этой формулы основано на параллельности оснований трапеции, и прямоугольными треугольниками, которые образует высота, проведенная из вершин верхнего основания.
Третий способ нахождения диагонали трапеции, если даны высота и средняя линия, актуален для равнобокой трапеции, то есть когда ее боковые стороны равны. Нужно начертить высоту и диагональ таким образом, чтобы они образовывали прямоугольный треугольник, тогда диагональ можно будет найти в нем по теореме Пифагора. Так как катет треугольника, лежащий на большем основании трапеции, состоит из меньшего основания и половины разности двух оснований по свойствам равнобокой трапеции, то он будет равен по значению средней линии:
Подставляя известные значения в теорему Пифагора, получаем:
d2=h2+m2