Прямоугольник — четырёхугольник, у которого все углы равны 90 градусов, т. е. прямые.
Диагональ прямоугольника — прямая проложенная из противоположных вершин прямоугольника.
Диагонали прямоугольника равны и они делят прямоугольник на два равных прямоугольных треугольника.
Чтобы найти диагональ прямоугольника необходимо вспомнить теорему Пифагора, ведь диагональ — это гипотенуза прямоугольного треугольника, а стороны (длина и ширина) прямоугольника являются катетами треугольника.
Как найти диагональ прямоугольника
Воспользуемся теоремой Пифагора и формулой
d= sqrt{a^2 + b^2}
d — диагональ квадрата
a — длина прямоугольника
b — ширина прямоугольника
Подставив в формулу вместо a длину прямоугольника, а вместо b — ширину прямоугольника и произведя расчет мы получим диагональ прямоугольника. Следует помнить, что у прямоугольника две диагонали и они равны между собой.
Диагональ прямоугольника онлайн калькулятор
Чтобы найти диагональ с помощью калькулятора введите длину и ширину прямоугольника и нажмите кнопку Рассчитать. В результате вы получите ответ и подробное решение.
Нахождение диагонали прямоугольника используется в различных жизненных ситуациях. К примеру, при проектировании фундамента дома необходимо проверить его диагонали — они должны быть равны между собой. Также на сайте можно рассчитать диагональ квадрата.
Ваша оценка
[Оценок: 169 Средняя: 3.1]
Диагональ прямоугольника Автор admin средний рейтинг 3.1/5 – 169 рейтинги пользователей
Загрузить PDF
Загрузить PDF
Диагональ — это отрезок, который соединяет две противолежащие вершины прямоугольника.[1]
В прямоугольнике две равные диагонали.[2]
Если известны стороны прямоугольника, диагональ можно найти по теореме Пифагора, потому что диагональ делит прямоугольник на два прямоугольных треугольника. Если стороны не даны, но известны другие величины, например, площадь и периметр или отношение сторон, можно найти стороны прямоугольника, а затем по теореме Пифагора вычислить диагональ.
-
1
-
2
-
3
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
4
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[5]
Вы найдете, то есть гипотенузу треугольника, а значит и диагональ прямоугольника.
Реклама
-
1
Запишите формулу для вычисления площади прямоугольника. Формула:
, где
— площадь прямоугольника,
— длина прямоугольника,
— ширина прямоугольника.[6]
(На рисунке вместо S использовано обозначение А.) -
2
В формулу подставьте значение площади прямоугольника. Это значение подставляется вместо
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула запишется так:
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула запишется так:
-
3
Перепишите формулу так, чтобы обособить
-
4
Запишите формулу для вычисления периметра прямоугольника. Формула:
, где
-
5
В формулу подставьте значение периметра прямоугольника. Это значение подставляется вместо
.
- Например, если периметр прямоугольника равен 24 сантиметра, формула запишется так:
.
- Например, если периметр прямоугольника равен 24 сантиметра, формула запишется так:
-
6
Разделите обе стороны уравнения на 2. Вы получите сумму сторон прямоугольника, а именно
.
-
7
В формулу подставьте выражение для вычисления
-
8
Избавьтесь от дроби. Для этого обе части уравнения умножьте на
-
9
Приравняйте уравнение к 0. Для этого из обеих сторон уравнения вычтите член с переменной первого порядка.
-
10
Упорядочьте члены уравнения. Первым членом будет член с переменной второго порядка, затем член с переменной первого порядка, а затем свободный член. При этом не забудьте про знаки («плюс» и «минус»), которые стоят перед членами. Обратите внимание, что уравнение запишется в виде квадратного уравнения.
-
11
Разложите квадратное уравнение на множители. Чтобы получить подробные инструкции, прочитайте эту статью.
-
12
Найдите
-
13
-
14
-
15
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
16
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[10]
Вы найдетеРеклама
-
1
-
2
-
3
В формулу подставьте значение площади прямоугольника. Это значение подставляется вместо
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула примет вид:
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула примет вид:
-
4
В формулу подставьте выражение, характеризующее отношение сторон. В случае прямоугольника можно подставить выражение для вычисления
-
5
Запишите квадратное уравнение. Для этого раскройте скобки и приравняйте уравнение к нулю.
-
6
Разложите квадратное уравнение на множители. Чтобы получить подробные инструкции, прочитайте эту статью.
-
7
Найдите
-
8
Подставьте найденное значение ширины (или длины) в уравнение, характеризующее отношение сторон. Так можно найти другую сторону прямоугольника.
-
9
-
10
-
11
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
12
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[16]
Вы найдетеРеклама
Об этой статье
Эту страницу просматривали 555 469 раз.
Была ли эта статья полезной?
Одна из основных фигур курса математики – прямоугольник.
Впервые о нем заговорили еще в Древнем Египте, а позже и в
Древней Греции. Именно свойства его диагоналей помогают
решить многие задания учебного курса. Подход, который
сейчас используется в геометрии разработал Евклид. Формулы,
представленные в данной статье, пригодятся как при решении
домашних упражнений, так и на ЕГЭ. Именно такие задачки
помогают набрать недостающие баллы, поэтому ими не стоит пренебрегать.
- Диагональ прямоугольника через его стороны
- Диагональ прямоугольника через площадь и известную сторону
- Диагональ прямоугольника через периметр и сторону
- Диагональ прямоугольника через диаметр описанной окружности
- Диагональ прямоугольника через радиус описанной окружности
- Диагональ прямоугольника через площадь и острый угол между диагоналями
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
- Что такое диагональ прямоугольника, когда требуется ее вычисление
Диагональ прямоугольника через его стороны
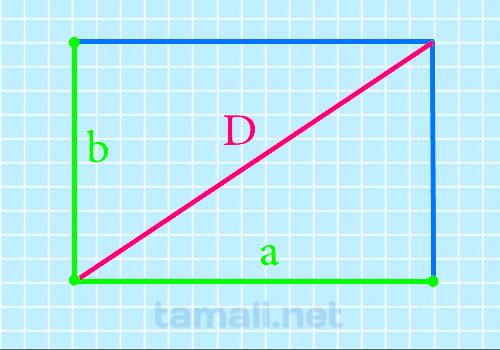
Если заданы хотя бы 2 стороны, то вычислить линию, соединяющую противоположные вершины, будет довольно просто. Применяется классическая теорема Пифагора. Достаточно подставить приведенные в дано числовые параметры в виде суммы квадратов под корнем:
Где a, b – это стороны, а d – прямая, которую мы ищем.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через площадь и известную сторону
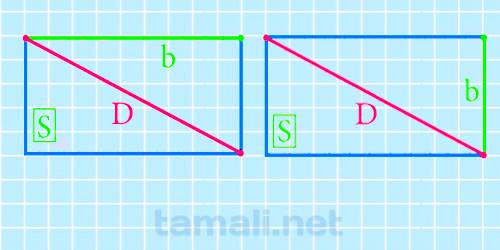
Когда в дано есть S и одна сторона, то узнать искомое значение можно используя следующее равенство:
Где D – это прямая, которую необходимо найти, a и b – любая заданная сторона, а S – площадь.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через периметр и сторону
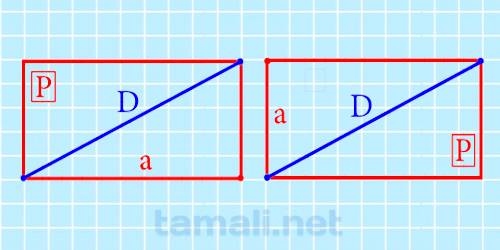
Когда задан периметр (сумма сторон) и, хотя бы одна сторона, отрезок, соединяющий несмежные точки высчитывают так:
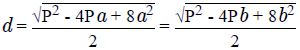
Где P – сумма сторон, a и b – любая заданная сторона.
Рассчитать искомый отрезок можно и через соотношение сторон и площадь.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через диаметр описанной окружности
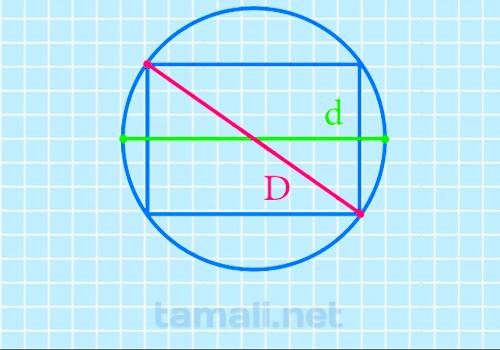
Поиск отрезка через описанную окружность еще более прост, здесь даже не придется проводить расчеты: D = d
Где d – это обозначенный диаметр.
Различить вписанную/описанную окружность легко. Когда геометрическое тело вписано куда-то, то оно всегда будет находиться в другой фигуре. Когда окружность описана, то она находится снаружи, она как бы описывает другое геометрическое тело. Описанные фигуры задевают собой точки, а вписанные – касаются сторон.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через радиус описанной окружности
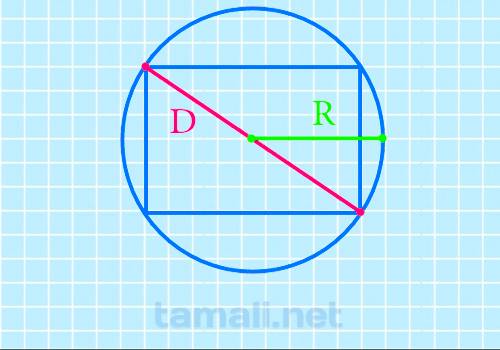
Для расчета искомого отрезка через описанную окружность нужно провести вычисления, где: D = 2R
Где R – это заданный радиус.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через площадь и острый угол между диагоналями
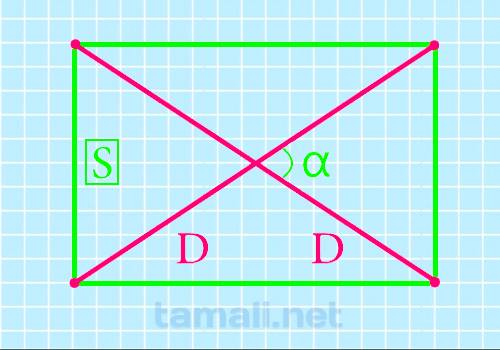
Если необходимо узнать прямую, соединяющую вершины 4-хугольника, это можно осуществить с помощью двух диагоналей. Для получения ответа к задаче понадобится sin β между ними и S (произведение длины и ширины).
Расчет проводится с равенством:
Где соответственно S – это площадь, а sin β – это острый угол, расположенный внутри фигуры (меж пересекающимися прямыми).
Если в 4-хугольнике расчертить 2 отрезка, объединяющие несмежные вершины, то они будут равны меж собой (все 4 отрезка), а точка пересечения разделит их пополам.
Пересечение всегда происходит в геометрическом центре самой фигурки. Этот же центр является центром описанной окружности.
Площадь (S):
Цифр после запятой:
Результат в:
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
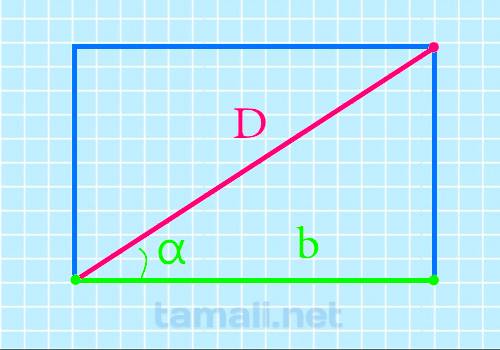
Когда одна из сторон 4-хугольника прилегает к углу, то просчитать отрезок, соединяющий вершины тоже возможно:
Где b – это сторона, прилегающая к углу, а cos a – это тот самый угол.
Косинус угла в треугольнике с прямым углом рассчитывается по формуле – длина соседней стороны, разделенная на гипотенузу. Синус – это противолежащий катет, разделенный на гипотенузу. Либо можно поступить еще проще, подсмотрев в таблицу Брадиса.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
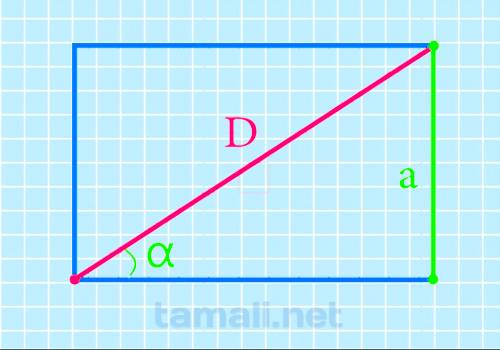
Чтобы найти нужный отрезок внутри четырехугольника, должен быть задан угол, прилегающий к искомому отрезку и сторона, противоположная углу:
Где a – это сторона четырехугольника, а sin a – это прилегающий угол.
Длинная сторона 4-хугольника– это длина, а короткая – его ширина. Помните, что каждая сторона одновременно является высотой.
Цифр после запятой:
Результат в:
Что такое диагональ прямоугольника, когда требуется ее вычисление
Прямоугольник – это частный случай параллелограмма. Иначе 4-хугольник с попарно равными сторонами, параллельными друг другу, а также равными прямыми углами по 90⁰. Сумма углов четырехугольника составляет 360⁰.
Диагональ разделяет фигуру на два новых элемента – треугольники с прямым углом. Это прямая, объединяющая противоположные вершины. Имея 2 прямоугольных треугольника, отрезок уже можно рассчитать по теореме Пифагора. По теореме гипотенуза – это квадрат из суммы катетов (обозначенных сторон треугольника), возведенных в квадрат.
Линии, соединяющие противоположные точки в четырехугольнике всегда пересекаются друг с другом.
Отрезок обозначают как d или D. Если названы все точки, то его можно называть в соответствии с ними – AC или BD.
Знания о линии, проходящей через несмежные точки 4-хугольника может понадобиться в легких геометрических упражнениях, так и в более сложных многоуровневых задачках, которые появляются на ЕГЭ. Свойства данного отрезка помогают находить важные параметры прямоугольника. Зная данные обеих линий, соединяющих противоположные углы, можно рассчитать S геометрического тела.
Перед решением любой геометрической задачки рекомендуется сделать чертеж и обозначить всю заданную информацию. Так будет значительно проще сосредоточиться на искомом значении.
Если регулярно решать тесты по геометрии, то формулы легче запомнятся, а их применение будет доведено до автоматизма.
Диагональ прямоугольника делит его на два прямоугольных треугольника и является гипотенузой обеих. Чтобы найти длину, проще всего воспользоваться теоремой Пифагора, которая в нашем случае будет звучать так
Это будет основная формула, но так как не всегда в условии заданы значения сторон прямоугольника, на помощь придут другие:
И теперь на нескольких примерах решим наше задание
Пример 1
найдем длину диагонали прямоугольника, если известна его а)сторона и периметр б) сторона и площадь.
Для этого сначала найдем неизвестную сторону, затем значения обеих сторон подставим в главную формулу
Пример 2
найдем длину диагонали прямоугольника, если известны его периметр и площадь.
Для этого составим систему уравнений, решим ее и подставим значения сторон в основную формулу
Пример 3
нужно найти длину диагонали прямоугольника, если известны его а)площадь и угол между диагональю и стороной б)периметр и угол между диагональю и стороной.
Решение аналогично предыдущему примеру
Как видим, без теоремы Пифагора во всех этих случаях никак не обойтись.
If your teacher has asked you to calculate the diagonal of a triangle, she’s already given you some valuable information. That phrasing tells you that you’re dealing with a right triangle, where two sides are perpendicular to each other (or to say it another way, they form a right triangle) and only one side is left to be “diagonal” to the others. That diagonal is called the hypotenuse, and you can find its length using the Pythagorean Theorem.
TL;DR (Too Long; Didn’t Read)
To find the length of the diagonal (or hypotenuse) of a right triangle, substitute the lengths of the two perpendicular sides into the formula a2 + b2 = c2, where a and b are the lengths of the perpendicular sides and c is the length of the hypotenuse. Then solve for c.
Pythagoras’ Theorem
The Pythagorean Theorem – sometimes also called Pythagoras’ Theorem, after the Greek philosopher and mathematician who discovered it – states that if a and b are the lengths of the perpendicular sides of a right triangle and c is the length of the hypotenuse, then:
a^2 + b^2 = c^2
In real-world terms, this means that if you know the length of any two sides of a right triangle, you can use that information to find out the length of the missing side. Note that this only works for right triangles.
Solving for the Hypotenuse
Assuming you know the lengths of the two non-diagonal sides of the triangle, you can substitute that information into the Pythagorean Theorem and then solve for c.
-
What if you know the length of the triangle’s diagonal and one other side? You can use the same formula to solve for the length of the unknown side. Just substitute in the lengths of the sides you do know, isolate the remaining letter variable on one side of the equals sign, and then solve for that letter, which represents the length of the unknown side.
Substitute the known values of a and b – the two perpendicular sides of the right triangle – into the Pythagorean Theorem. So if the two perpendicular sides of the triangle measure 3 and 4 units respectively, you’d have:
3^2 + 4^2 = c^2
Work the exponents (when possible – in this case you can) and simplify like terms. This gives you:
9 + 16 = c^2
Followed by:
c^2 = 25
Take the square root of both sides, the final step in solving for c. This gives you:
c = sqrt{25}= 5
So the length of the diagonal, or hypotenuse, of this triangle is 5 units.
