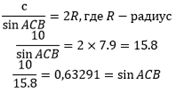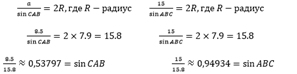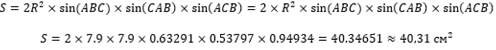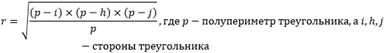Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
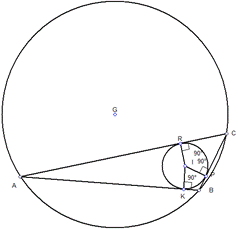
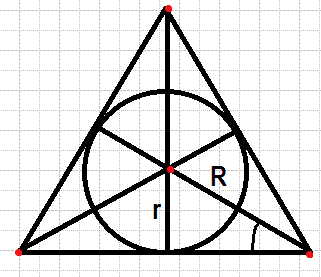
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac<1><2>ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Как найти диагональ треугольника вписанного в окружность
Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 11.
Это задание ещё не решено, приводим решение прототипа.
Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 5.
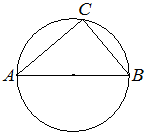
Угол A является прямым, он опирается на диагональ BD, которая является диаметром:
Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
[spoiler title=”источники:”]
http://ege.sdamgia.ru/test?likes=27902
http://ege-study.ru/ru/ege/materialy/matematika/vpisannyj-i-opisannyj-treugolnik-vpisannaya-i-opisannaya-okruzhnost/
[/spoiler]
Содержание
- Определение
- Формулы
- Радиус вписанной окружности в треугольник
- Радиус описанной окружности около треугольника
- Площадь треугольника
- Периметр треугольника
- Сторона треугольника
- Средняя линия треугольника
- Высота треугольника
- Свойства
- Доказательство
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — не диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
[ r = frac{S}{(a+b+c)/2} ]
- Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
[ r = frac{S}{frac{1}{2}P} ]
- Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
[ r = sqrt{frac{(p-a)(p-b)(p-c)}{p}} ]
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
[ R = frac{AC}{2 sin angle B} ]
- Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
[ R = frac{abc}{4S} ]
- Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:[ R = frac{abc}{4sqrt{p(p-a)(p-b)(p-c)}} ]
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:[ S = pr ]
- Площадь треугольника вписанного в окружность,
если известен полупериметр:[ S = sqrt{p(p-a)(p-b)(p-c)} ]
- Площадь треугольника вписанного в окружность,
если известен высота и основание:[ S = frac{1}2 ah ]
- Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:[ S = frac{a^2}{2cdot (sin(α)⋅sin(β)) : sin(180 — (α + β))} ]
- Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:[ S = frac{1}{2}ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
[ P = a + b + c ]
- Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
[ P = frac{2S}{r} ]
- Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:[ P = sqrt{ b2 + с2 — 2 * b * с * cosα} + (b + с) ]
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:[ a = sqrt{b^2+c^2 -2bc cdot cos alpha} ]
- Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
[ a = frac{b · sin alpha }{sin β} ]
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
[ l = frac{AB}{2} ]
- Средняя линия треугольника вписанного в окружность,
если известны две стороны, ни одна из них не является
основанием, и косинус угла между ними:
[ l = frac{sqrt{b^2+c^2-2bc cdot cos alpha}}{2} ]
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:[ h = frac{2S}{a} ]
- Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:[ h = b cdot sin alpha ]
- Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:[ h = frac{bc}{2R} ]
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
Дано: окружность и треугольник,
которые изображены на рисунке 2.
Доказать: окружность описана
около треугольника.
Доказательство:
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
Следовательно: окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
В современном машиностроении используется масса элементов и запчастей, которые имеют в своей структуре как внешние окружности, так и внутренние. Самым ярким примером могут служить корпус подшипника, детали моторов, узлы ступицы и многое другое. При их изготовлении применяются не только высокотехнологичные приспособления, но и знания из геометрии, в частности информация об окружностях треугольника. Более детально с подобным знаниями познакомимся ниже….
Какая окружность вписана, а какая описана
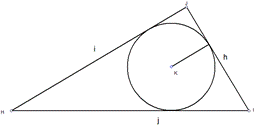
Прежде всего вспомним, что окружностью называется бесконечное множество точек, удаленных на одинаковом расстоянии от центра. Если внутри многоугольника допускается построить окружность, которая с каждой стороной будет иметь только одну общую точку пересечения, то она будет называться вписанной. Описанной окружностью (не круг, это разные понятия) называется такое геометрическое место точек, при котором у построенной фигуры с заданным многоугольником общими точками будут только вершины многоугольника. Ознакомимся с этими двумя понятиями на более наглядном примере (см. рис 1.).
Рисунок 1. Вписанная и описанная окружности треугольника
На изображении построены две фигуры большого и малого диаметров, центры которых находятся G и I. Окружность большего значения называется описанной окр-тью Δ ABC, а малого – наоборот, вписанной в Δ ABC.
Для того чтобы описать вокруг треугольника окр-ть, требуется провести через середину каждой стороны перпендикулярную прямую (т.е. под углом 90°) – это точка пересечения, она играет ключевую роль. Именно она будет представлять собой центр описанной окружности. Перед тем как найти окружность, ее центр в треугольнике, требуется построить для каждого угла биссектрису, после чего выделить точку пересечения прямых. Она в свою очередь будет центром вписанной окр-ти, а ее радиус при любых условиях будет перпендикулярен любой из сторон.
На вопрос:«Какое количество окружностей вписанных может быть для многоугольника с тремя углами?» ответим сразу, что в любой треугольник можно вписать окружность и притом только одну. Потому что существует только одна точка пересечения всех биссектрис и одна точка пересечения перпендикуляров, исходящих из середин сторон.
Свойство окружности, которой принадлежат вершины треугольника
Описанная окружность, которая зависит от длин сторон при основании, имеет свои свойства. Укажем свойства описанной окружности:
- Центр описанной окружности для прямоугольного треугольника находится на середине гипотенузы, у острого – внутри самого треугольника, а для тупоугольного – за ее пределами.
- Диаметр любой описанной окр-сти равен половине отношения стороны и синуса угла, который принадлежит ей, в виде формулы можно представить следующим образом:
- Зная радиус описанной окружности и значения углов, можно найти значение площади, не прибегая к использованию длин сторон, по следующей формуле:
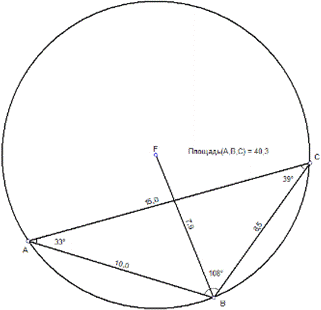
Для того чтобы более наглядно понять принцип описанной окружности, решим простую задачу. Допустим, что дан треугольник Δ ABC, стороны которого равны 10, 15 и 8,5 см. Радиус описанной окружности около треугольника (FB) составляет 7,9 см. Найти значение градусной меры каждого угла и через них площадь треугольника.
Рисунок 2. Поиск радиуса окружности через отношение сторон и синусов углов
Решение: опираясь на ранее указанную теорему синусов, найдем значение синуса каждого угла в отдельности. По условию известно, что сторона АВ равна 10 см. Вычислим значение С:
Используя значения таблицы Брадиса, узнаем, что градусная мера угла С равна 39°. Таким же методом найдем и остальные меры углов:
Откуда узнаем, что CAB = 33°, а ABC = 108°. Теперь, зная значения синусов каждого из углов и радиус, найдем площадь, подставляя найденные значения:
Ответ: площадь треугольника равна 40,31 см², а углы равны соответственно 33°, 108° и 39°.
Важно! Решая задачи подобного плана, будет нелишним всегда иметь таблицы Брадиса либо соответствующее приложение на смартфоне, так как вручную процесс может затянуться на длительное время. Также для большей экономии времени не требуется обязательно строить все три середины перпендикуляра либо три биссектрисы. Любая третья из них всегда будет пересекаться в точке пересечения первых двух. А для ортодоксального построения обычно третью дорисовывают. Может, это неправильно в вопросе алгоритма, но на ЕГЭ или других экзаменах это здорово экономит время.
Исчисление радиуса вписанной окружности
Все точки окружности одинаково удалены от ее центра на одинаковом расстоянии. Длину этого отрезка (от и до) называют радиусом. В зависимости от того, какую окр-ть мы имеем, различают два вида – внутренний и внешний. Каждый из них вычисляется по собственной формуле и имеет прямое отношение к вычислению таких параметров, как:
- площадь,
- градусная мера каждого угла,
- длины сторон и периметр.
Рисунок 3. Расположение вписанной окружности внутри треугольника
Вычислить длину расстояния от центра до точки соприкосновения с любой из сторон можно такими способами: через стороны, высоты, боковые стороны и углы (для равнобокого треугольника).
Использование полупериметра
Полупериметром называется половина суммы длин всех сторон. Такой способ считается самым популярным и универсальным, потому как независимо от того, какой тип треугольника дан по условию, он подходит для всех. Порядок вычисления имеет следующий вид:
Если дан «правильный»
Одним из малых преимуществ «идеального» треугольника является то, что вписанная и описанная окружности имеют центр в одной точке. Это удобно при построении фигур. Однако в 80% случаев ответ получается «некрасивым». Тут имеется ввиду, что очень редко радиус вписанной окр-ти будет целым натуральным числом, скорее наоборот. Для упрощенного исчисления используется формула радиуса вписанной окружности в треугольник:
Если боковины одинаковой длины
Одним из подтипов задач на гос. экзаменах будет нахождение радиуса вписанной окружности треугольника, две стороны которого равны между собой, а третья нет. В таком случае рекомендуем использовать этот алгоритм, который даст ощутимую экономию времени на поиск диаметра вписанной окр-ти. Радиус вписанной окружности в треугольник с равными «боковыми» вычисляется по формуле:
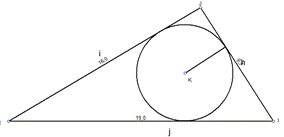
Более наглядное применение указанных формул продемонстрируем на следующей задаче. Пускай имеем треугольник (Δ HJI), в который вписана окр-ть в точке K. Длина стороны HJ = 16 см, JI = 9,5 см и сторона HI равна 19 см (рисунок 4). Найти радиус вписанной окр-ти, зная стороны.
Рисунок 4. Поиск значения радиуса вписанной окружности
Решение: для нахождения радиуса вписанной окр-ти найдем полупериметр:
Отсюда, зная механизм вычисления, узнаем следующее значение. Для этого понадобятся длины каждой из сторон (дано по условию), а также половину периметра, получается:
Отсюда следует, что искомый радиус равен 3,63 см. Согласно условию, все стороны равны, тогда искомый радиус будет равен:
При условии, если многоугольник равнобокий (например, i = h = 10 см, j = 8 см), диаметр внутренней окр-ти с центром в точке K будет равен:
В условии задачи может даваться треугольник с углом 90°, в таком случае запоминать формулу нет необходимости. Гипотенуза треугольника будет равна диаметру. Более наглядно это выглядит так:
Важно! Если задана задача на поиск внутреннего радиуса, не рекомендуем проводить вычисления через значения синусов и косинусов углов, табличное значение которых точно не известно. В случае, если иначе узнать длину невозможно, не пытайтесь «вытащить» значение из-под корня. В 40% задач полученное значение будет трансцендентным (т.е. бесконечным), а комиссия может не засчитать ответ (даже если он будет правильным) из-за его неточности или неправильной формы подачи. Особое внимание уделите тому, как может видоизменяться формула радиуса описанной окружности треугольника в зависимости от предложенных данных. Такие «заготовки» позволяют заранее «видеть» сценарий решения задачи и выбрать наиболее экономное решение.
Радиус внутренней окружности и площадь
Для того чтобы вычислить площадь треугольника, вписанного в окружность, используют лишь радиус и длины сторон многоугольника:
Если в условии задачи напрямую не дано значение радиуса, а только площадь, то указанная формула площади трансформируется в следующую:
Рассмотрим действие последней формулы на более конкретном примере. Предположим, что дан треугольник, в который вписана окр-ть. Площадь окр-ти составляет 4π, а стороны равны соответственно 4, 5 и 6 см. Вычислим площадь заданного многоугольника при помощи вычисления полупериметра.
Используя вышеуказанный алгоритм, вычислим площадь треугольника через радиус вписанной окружности:
В силу того, что в любой треугольник можно вписать окружность, число вариаций нахождения площади значительно увеличивается. Т.е. поиск площади треугольника, включает в себя обязательное знание длины каждой стороны, а также значение радиуса.
Треугольник, вписанный в окружность геометрия 7 класс
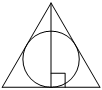
Прямоугольные треугольники, вписанные в окружность
Вывод
Из указанных формул можно убедиться, что сложность любой задачи с использованием вписанной и описанной окружностей заключается только в дополнительных действия по поиску требуемых значений. Задачи подобного типа требуют только досконально понимания сути формул, а также рациональности их применения. Из практики решения отметим, что в будущем центр описанной окружности будет фигурировать и в дальнейших темах геометрии, поэтому запускать ее не следует. В противном случае решение может затянуться с использованием лишних ходов и логических выводов.
Следующие задачи на эту тему предлагает открытый банк заданий ФИПИ к ОГЭ по математике (раздел геометрия). Любое из них может вам попасться на ОГЭ в этом году.
Реальные задания по геометрии из банка ФИПИ
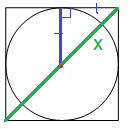
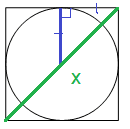
Радиус вписанной в квадрат окружности равен 2√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти.
Запишем равенство, используя теорему Пифагорах2=(2√2)2+(2√2)2 = 4*2 + 4*2 =16
х = 4
2х = 8Ответ: 8
Второй способ
Диагональ делит квадрат на 2 равных прямоугольных равнобедренных треугольника.
Диаметр окружности равен катету треугольника и равен удвоенному радиусу
d = 2 * 2√2 = 4√2
По теореме Пифагора можем найти гипотенузу,
х2=(4√2)2+(4√2)2 = 16*2 + 16*2 =64
х = 8Ответ: 8
7E4CCF
Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти.
Запишем равенство, используя теорему Пифагорах=2√((4√2)2+(4√2)2)=2√(16*2+16*2)=2*8=16
Ответ: 16
C84B98
Радиус вписанной в квадрат окружности равен 6√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти.
Запишем равенство, используя теорему Пифагорах=2√((6√2)2+(6√2)2)=2√(36*2+36*2)=2*12=24
Ответ: 24
40FF58
Радиус вписанной в квадрат окружности равен 8√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти.
Запишем равенство, используя теорему Пифагорах=2√((8√2)2+(8√2)2)=2√(64*2+64*2)=2*16=32
Ответ: 32
4E821A
Радиус вписанной в квадрат окружности равен 10√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти.
Запишем равенство, используя теорему Пифагорах=2√((10√2)2+(10√2)2)=2√(100*2+100*2)=2*20=40
Ответ: 40
E12730
Радиус вписанной в квадрат окружности равен 14√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти.
Запишем равенство, используя теорему Пифагорах=2√((14√2)2+(14√2)2)=2√(196*2+196*2)=2*28=56
Ответ: 56
17DF0C
Радиус вписанной в квадрат окружности равен 16√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти.
Запишем равенство, используя теорему Пифагорах=2√((16√2)2+(16√2)2)=2√(256*2+256*2)=2*32=64
Ответ: 64
E4E4A6
Радиус вписанной в квадрат окружности равен 18√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти.
Запишем равенство, используя теорему Пифагорах=2√((18√2)2+(18√2)2)=2√(324*2+324*2)=2*36=72
Ответ: 72
D173D1
Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти.
Запишем равенство, используя теорему Пифагорах=2√((22√2)2+(22√2)2)=2√(484*2+484*2)=2*44=88
Ответ: 88
4DCFDB
Радиус вписанной в квадрат окружности равен 24√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти.
Запишем равенство, используя теорему Пифагорах=2√((24√2)2+(24√2)2)=2√(576*2+576*2)=2*48=96
Ответ: 96
7B13AD
Радиус окружности, описанной около квадрата, равен 4√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$left(2ast4surd2right)^2=2x^2\x^2=frac{left(2ast4surd2right)^2}2\x=sqrt{frac{left(2ast4surd2right)^2}2}\х=frac{2ast4surd2}{sqrt2}=8$
Ответ: 8
CF5BF1
Радиус окружности, описанной около квадрата, равен 16√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$left(2ast16surd2right)^2=2x^2\x^2=frac{left(2ast16surd2right)^2}2\x=sqrt{frac{left(2ast16surd2right)^2}2}\х=frac{2ast16surd2}{sqrt2}=32$
Ответ: 32
CD5252
Радиус окружности, описанной около квадрата, равен 14√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$left(2ast14surd2right)^2=2x^2\x^2=frac{left(2ast14surd2right)^2}2\x=sqrt{frac{left(2ast14surd2right)^2}2}\х=frac{2ast14surd2}{sqrt2}=28$
Ответ: 28
B927DB
Радиус окружности, описанной около квадрата, равен 26√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$left(2ast26surd2right)^2=2x^2\x^2=frac{left(2ast26surd2right)^2}2\x=sqrt{frac{left(2ast26surd2right)^2}2}\х=frac{2ast26surd2}{sqrt2}=52$
Ответ: 52
32A97B
Радиус окружности, описанной около квадрата, равен 34√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$left(2ast34surd2right)^2=2x^2\x^2=frac{left(2ast34surd2right)^2}2\x=sqrt{frac{left(2ast34surd2right)^2}2}\х=frac{2ast34surd2}{sqrt2}=68$
Ответ: 68
20ED7A
Радиус окружности, описанной около квадрата, равен 28√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$left(2ast28surd2right)^2=2x^2\x^2=frac{left(2ast28surd2right)^2}2\x=sqrt{frac{left(2ast28surd2right)^2}2}\х=frac{2ast28surd2}{sqrt2}=56$
Ответ: 56
F27430
Радиус окружности, описанной около квадрата, равен 18√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$left(2ast18surd2right)^2=2x^2\x^2=frac{left(2ast18surd2right)^2}2\x=sqrt{frac{left(2ast18surd2right)^2}2}\х=frac{2ast18surd2}{sqrt2}=36$
Ответ: 36
B07B04
Радиус окружности, описанной около квадрата, равен 22√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$left(2ast22surd2right)^2=2x^2\x^2=frac{left(2ast22surd2right)^2}2\x=sqrt{frac{left(2ast22surd2right)^2}2}\х=frac{2ast22surd2}{sqrt2}=44$
Ответ: 44
C0C526
Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$left(2ast36surd2right)^2=2x^2\x^2=frac{left(2ast36surd2right)^2}2\x=sqrt{frac{left(2ast36surd2right)^2}2}\х=frac{2ast36surd2}{sqrt2}=72$
Ответ: 72
466413
Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$left(2ast32surd2right)^2=2x^2\x^2=frac{left(2ast32surd2right)^2}2\x=sqrt{frac{left(2ast32surd2right)^2}2}\х=frac{2ast32surd2}{sqrt2}=64$
Ответ: 64
FA41B7
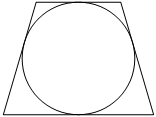
Радиус окружности, вписанной в трапецию, равен 16. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*16=32
Ответ: 32
D00494
Радиус окружности, вписанной в трапецию, равен 18. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*18=36
Ответ: 36
BC46E4
Радиус окружности, вписанной в трапецию, равен 34. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*34=68
Ответ: 68
FE4FCD
Радиус окружности, вписанной в трапецию, равен 26. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*26=52
Ответ: 52
E5AF5A
Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*48=96
Ответ: 96
7C5CEF
Радиус окружности, вписанной в трапецию, равен 42. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*16=42
Ответ: 84
F45C93
Радиус окружности, вписанной в трапецию, равен 36. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*36=72
Ответ: 72
6623F6
Радиус окружности, вписанной в трапецию, равен 38. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*38=76
Ответ: 76
4B2B64
Радиус окружности, вписанной в трапецию, равен 24. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*24=48
Ответ: 48
4A4F32
Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*32=64
Ответ: 64
4CC220
Радиус окружности, вписанной в равнобедренную трапецию, равен 12. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*12=24
Ответ: 24
1314AB
Радиус окружности, вписанной в равнобедренную трапецию, равен 14. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*14=28
Ответ: 28
897F1A
Радиус окружности, вписанной в равнобедренную трапецию, равен 30. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*30=60
Ответ: 60
03DDD9
Радиус окружности, вписанной в равнобедренную трапецию, равен 22. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*22=44
Ответ: 44
60F5F8
Радиус окружности, вписанной в равнобедренную трапецию, равен 44. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*44=88
Ответ: 88
5B197F
Радиус окружности, вписанной в равнобедренную трапецию, равен 38. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*38=76
Ответ: 76
B8967A
Радиус окружности, вписанной в равнобедренную трапецию, равен 32. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*32=64
Ответ: 64
B1F719
Радиус окружности, вписанной в равнобедренную трапецию, равен 34. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*34=68
Ответ: 68
F794FE
Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*20=40
Ответ: 40
82E915
Радиус окружности, вписанной в равнобедренную трапецию, равен 28. Найдите высоту этой трапеции.
Решение:
Ответ: Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*28=56
Ответ: 56
788577
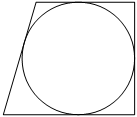
Радиус окружности, вписанной в прямоугольную трапецию, равен 10. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*10=20
Ответ: 20
1AE9FC
Радиус окружности, вписанной в прямоугольную трапецию, равен 12. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*12=24
Ответ: 24
301A24
Радиус окружности, вписанной в прямоугольную трапецию, равен 28. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*28=56
Ответ: 56
81B7DF
Радиус окружности, вписанной в прямоугольную трапецию, равен 20. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*20=40
Ответ: 40
B404D2
Радиус окружности, вписанной в прямоугольную трапецию, равен 42. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*42=84
Ответ: 84
654235
Радиус окружности, вписанной в прямоугольную трапецию, равен 36. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*36=72
Ответ: 72
2231C2
Радиус окружности, вписанной в прямоугольную трапецию, равен 30. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*30=60
Ответ: 60
74C85E
Радиус окружности, вписанной в прямоугольную трапецию, равен 32. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*32=64
Ответ: 64
7CF9EB
Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*18=36
Ответ: 36
D5823B
Радиус окружности, вписанной в прямоугольную трапецию, равен 26. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*26=52
Ответ: 52
288717
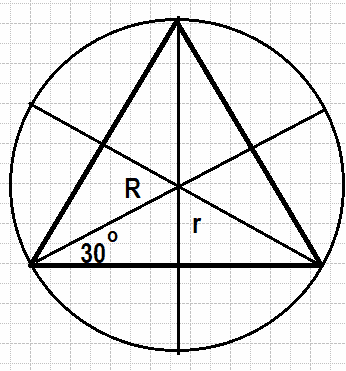
Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r5*3=15
Ответ: 15
E41C75
Радиус окружности, вписанной в равносторонний треугольник, равен 7. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r7*3=21
Ответ: 21
A73120
Радиус окружности, вписанной в равносторонний треугольник, равен 8. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r8*3=24
Ответ: 24
55F2B4
Радиус окружности, вписанной в равносторонний треугольник, равен 15. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r3*15=45
Ответ: 45
25FB46
Радиус окружности, вписанной в равносторонний треугольник, равен 18. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r3*18=54
Ответ: 54
07E18E
Радиус окружности, вписанной в равносторонний треугольник, равен 4. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r4*3=12
Ответ: 12
490AD4
Радиус окружности, вписанной в равносторонний треугольник, равен 9. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r9*3=27
Ответ: 27
209F1B
Радиус окружности, вписанной в равносторонний треугольник, равен 11. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r11*3=33
Ответ: 33
907529
Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r12*3=36
Ответ: 36
A44A54
Радиус окружности, вписанной в равносторонний треугольник, равен 14. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r14*3=42
Ответ: 42
A3A364
Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R6*1.5=9
Ответ: 9
6606B6
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R10*1.5=15
Ответ: 15
711898
Радиус окружности, описанной около равностороннего треугольника, равен 8. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R8*1.5=12
Ответ: 12
29E0BA
Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R16*1.5=24
Ответ: 24
23E335
Радиус окружности, описанной около равностороннего треугольника, равен 18. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R18*1.5=27
Ответ: 27
8CA0CF
Радиус окружности, описанной около равностороннего треугольника, равен 4. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R4*1.5=6
Ответ: 6
40E6BC
Радиус окружности, описанной около равностороннего треугольника, равен 20. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R20*1.5=30
Ответ: 30
59CE06
Радиус окружности, описанной около равностороннего треугольника, равен 2. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R2*1.5=3
Ответ: 3
FCF728
Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R12*1.5=18
Ответ: 18
F7AB41
Радиус окружности, описанной около равностороннего треугольника, равен 14. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R14*1.5=21
Ответ: 21
6B0A52
Радиус окружности, вписанной в равносторонний треугольник, равен 2√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4left(2sqrt3right)^2=left(2sqrt3right)^2+x^2\x^2=;3left(2sqrt3right)^2\х^2=3ast4ast3\х=sqrt{36}\х=6$
6*2=12
Ответ: 12
D07B18
Радиус окружности, вписанной в равносторонний треугольник, равен 3√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4left(3surd3right)^2=left(3surd3right)^2+x^2\x^2=;3left(3surd3right)^2\х^2=3ast9ast3\х=sqrt{81}\х=9$
9*2=18
Ответ: 18
AB32B8
Радиус окружности, вписанной в равносторонний треугольник, равен 4√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4left(4surd3right)^2=left(4surd3right)^2+x^2\x^2=;3left(4surd3right)^2\х^2=3ast16ast3\х=sqrt{144}\х=12$
12*2=24
Ответ: 24
C03CA1
Радиус окружности, вписанной в равносторонний треугольник, равен 5√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4left(5surd3right)^2=left(5surd3right)^2+x^2\x^2=;3left(5surd3right)^2\х^2=3ast25ast3\х=sqrt{225}\х=15$
15*2=30
Ответ: 30
7F1E51
Радиус окружности, вписанной в равносторонний треугольник, равен 6√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4left(6surd3right)^2=left(6surd3right)^2+x^2\x^2=;3left(6surd3right)^2\х^2=3ast36ast3\х=sqrt{324}\х=18$
18*2=36
Ответ: 36
047CDE
Радиус окружности, вписанной в равносторонний треугольник, равен 7√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4left(7surd3right)^2=left(7surd3right)^2+x^2\x^2=;3left(7surd3right)^2\х^2=3ast49ast3\х=sqrt{441}\х=21$
21*2=12
Ответ: 42
CAC621
Радиус окружности, вписанной в равносторонний треугольник, равен 8√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4left(8surd3right)^2=left(8surd3right)^2+x^2\x^2=;3left(8surd3right)^2\х^2=3ast64ast3\х=sqrt{576}\х=24$
24*2=48
Ответ: 48
41D84A
Радиус окружности, вписанной в равносторонний треугольник, равен 9√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4left(9surd3right)^2=left(9surd3right)^2+x^2\x^2=;3left(9surd3right)^2\х^2=3ast81ast3\х=sqrt{729}\х=27$
27*2=54
Ответ: 54
6D0284
Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4left(10surd3right)^2=left(10surd3right)^2+x^2\x^2=;3left(10surd3right)^2\х^2=3ast100ast3\х=sqrt{900}\х=30$
30*2=60
Ответ: 60
F99836
Радиус окружности, вписанной в равносторонний треугольник, равен 11√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4left(11surd3right)^2=left(11surd3right)^2+x^2\x^2=;3left(11surd3right)^2\х^2=3ast121ast3\х=sqrt{1089}\х=33$
33*2=66
Ответ: 66
79607C
Решение:
Радиус окружности, описанной около равностороннего треугольника, равен 2√3. Найдите длину стороны этого треугольника.
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$left(2surd3right)^2=left(frac{2surd3}2right)^2+x^2\x^2=;4{surd3}^2-surd3^2\х^2=3sqrt3^2\х=sqrt{3ast3}\х=3$
3*2=6
Ответ: 6
4F011
Радиус окружности, описанной около равностороннего треугольника, равен 3√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$left(3surd3right)^2=left(frac{3surd3}2right)^2+x^2\x^2=;frac{4left(3surd3right)^2}4-frac{left(3surd3right)}4^2\х^2=frac{3left(3surd3right)^2}4\х=sqrt{frac{3ast9ast3}4}\х=sqrt{frac{81}4}=frac92=4.5$
4.5*2=9
Ответ: 9
DDDC3E
Радиус окружности, описанной около равностороннего треугольника, равен 4√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$left(4surd3right)^2=left(frac{4surd3}2right)^2+x^2\x^2=;frac{4left(4surd3right)^2}4-frac{left(4surd3right)}4^2\х^2=frac{3left(4surd3right)^2}4\х=sqrt{frac{3ast16ast3}4}\х=sqrt{frac{144}4}=frac{12}2=6$
6*2=12
Ответ: 12
4864D6
Радиус окружности, описанной около равностороннего треугольника, равен 5√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$left(5surd3right)^2=left(frac{5surd3}2right)^2+x^2\x^2=;frac{4left(5surd3right)^2}4-frac{left(5surd3right)}4^2\х^2=frac{3left(5surd3right)^2}4\х=sqrt{frac{3ast25ast3}4}\х=sqrt{frac{225}4}=frac{15}2=7.5$
7.5*2=15
Ответ: 15
297C02
Радиус окружности, описанной около равностороннего треугольника, равен 6√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$left(6surd3right)^2=left(frac{6surd3}2right)^2+x^2\x^2=;frac{4left(6surd3right)^2}4-frac{left(6surd3right)}4^2\х^2=frac{3left(6surd3right)^2}4\х=sqrt{frac{3ast36ast3}4}\х=sqrt{frac{324}4}=frac{18}2=9$
9*2=18
Ответ: 18
8E90C6
Радиус окружности, описанной около равностороннего треугольника, равен 7√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$left(7surd3right)^2=left(frac{7surd3}2right)^2+x^2\x^2=;frac{4left(7surd3right)^2}4-frac{left(7surd3right)}4^2\х^2=frac{3left(7surd3right)^2}4\х=sqrt{frac{3ast49ast3}4}\х=sqrt{frac{441}4}=frac{21}2=10.5$
10.5*2=21
Ответ: 21
48D77B
Радиус окружности, описанной около равностороннего треугольника, равен 8√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$left(8surd3right)^2=left(frac{8surd3}2right)^2+x^2\x^2=;frac{4left(8surd3right)^2}4-frac{left(8surd3right)}4^2\х^2=frac{3left(8surd3right)^2}4\х=sqrt{frac{3ast64ast3}4}\х=sqrt{frac{576}4}=frac{24}2=12$
12*2=24
Ответ: 24
426C70
Радиус окружности, описанной около равностороннего треугольника, равен 9√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$left(9surd3right)^2=left(frac{9surd3}2right)^2+x^2\x^2=;frac{4left(9surd3right)^2}4-frac{left(9surd3right)}4^2\х^2=frac{3left(9surd3right)^2}4\х=sqrt{frac{3ast81ast3}4}\х=sqrt{frac{729}4}=frac{27}2=13.5$
13.5*2=26
Ответ: 26
71EE14
Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$left(10surd3right)^2=left(frac{10surd3}2right)^2+x^2\x^2=;frac{4left(10surd3right)^2}4-frac{left(10surd3right)}4^2\х^2=frac{3left(10surd3right)^2}4\х=sqrt{frac{3ast100ast3}4}\х=sqrt{frac{900}4}=frac{30}2=15$
15*2=30
Ответ: 30
E566FC
Радиус окружности, описанной около равностороннего треугольника, равен 11√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$left(11surd3right)^2=left(frac{11surd3}2right)^2+x^2\x^2=;frac{4left(11surd3right)^2}4-frac{left(11surd3right)}4^2\х^2=frac{3left(11surd3right)^2}4\х=sqrt{frac{3ast121ast3}4}\х=sqrt{frac{1089}4}=frac{33}2=16.5$
16.5*2=33
Ответ: 33
07781B
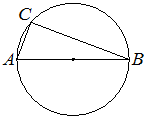
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 25. Найдите AC, если BC=48.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем AC и подставляем значения.
$left(2frac{AB}2right)^2=AC^2+CB^2\AC^2=4left(frac{AB}2right)^2-CB^2\AC=sqrt{4left(frac{AB}2right)^2-CB^2}\AC=sqrt{4ast25^2-48^2}\AC=sqrt{4ast625-2304}=sqrt{196}=14$
Ответ: 14
CABA26
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найдите BC, если AC=32.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем BC и подставляем значения.
$left(2frac{AB}2right)^2=AC^2+CB^2\CB^2=4left(frac{AB}2right)^2-AC^2\CB=sqrt{4left(frac{AB}2right)^2-AC^2}\CB=sqrt{4ast20^2-32^2}\CB=sqrt{4ast400-1024}=sqrt{1600-1024}=24$
Ответ: 24
E7C22E
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 13. Найдите AC, если BC=24.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем AC и подставляем значения.
$left(2frac{AB}2right)^2=AC^2+CB^2\AC^2=4left(frac{AB}2right)^2-CB^2\AC=sqrt{4left(frac{AB}2right)^2-CB^2}\AC=sqrt{4ast13^2-24^2}\AC=sqrt{4ast169-576}=sqrt{676-576}=10$
Ответ: 10
4045A6
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 17. Найдите AC, если BC=30.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем AC и подставляем значения.
$left(2frac{AB}2right)^2=AC^2+CB^2\AC^2=4left(frac{AB}2right)^2-CB^2\AC=sqrt{4left(frac{AB}2right)^2-CB^2}\AC=sqrt{4ast17^2-30^2}\AC=sqrt{4ast289-900}=sqrt{256}=16$
Ответ: 16
1845C2
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем BC и подставляем значения.
$left(2frac{AB}2right)^2=AC^2+CB^2\CB^2=4left(frac{AB}2right)^2-AC^2\CB=sqrt{4left(frac{AB}2right)^2-AC^2}\CB=sqrt{4ast10^2-16^2}\CB=sqrt{4ast100-256}=sqrt{400-256}=12$
Ответ: 12
C8A9ED
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем BC и подставляем значения.
$left(2frac{AB}2right)^2=AC^2+CB^2\CB^2=4left(frac{AB}2right)^2-AC^2\CB=sqrt{4left(frac{AB}2right)^2-AC^2}\CB=sqrt{4ast15^2-24^2}\CB=sqrt{4ast225-576}=sqrt{324}=18$
Ответ: 18
EF5960
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 14,5. Найдите AC, если BC=21.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем AC и подставляем значения.
$left(2frac{AB}2right)^2=AC^2+CB^2\AC^2=4left(frac{AB}2right)^2-CB^2\AC=sqrt{4left(frac{AB}2right)^2-CB^2}\AC=sqrt{4ast14.5^2-12^2}\AC=sqrt{4ast210.25-900}=sqrt{841-441}=20$
Ответ: 20
6D03EB
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20,5. Найдите BC, если AC=9.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем BC и подставляем значения.
$left(2frac{AB}2right)^2=AC^2+CB^2\CB^2=4left(frac{AB}2right)^2-AC^2\CB=sqrt{4left(frac{AB}2right)^2-AC^2}\CB=sqrt{4ast20.5^2-9^2}\CB=sqrt{4ast420.25-81}=sqrt{1600}=40$
Ответ: 40
E7626A
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 8,5. Найдите BC, если AC=8.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем BC и подставляем значения.
$left(2frac{AB}2right)^2=AC^2+CB^2\CB^2=4left(frac{AB}2right)^2-AC^2\CB=sqrt{4left(frac{AB}2right)^2-AC^2}\CB=sqrt{4ast8.5^2-8^2}\CB=sqrt{4ast72.25-64}=sqrt{225}=15$
Ответ: 15
748A0C
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 6,5. Найдите AC, если BC=12.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем AC и подставляем значения.
$left(2frac{AB}2right)^2=AC^2+CB^2\AC^2=4left(frac{AB}2right)^2-CB^2\AC=sqrt{4left(frac{AB}2right)^2-CB^2}\AC=sqrt{4ast6.5^2-12^2}\AC=sqrt{4ast42.25-900}=sqrt{169-144}=5$
Ответ: 5
7B6202
Задания с развернутым ответом
Углы B и C треугольника ABC равны соответственно 71° и 79°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 8.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
6AFB28
Углы B и C треугольника ABC равны соответственно 73° и 77°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 9.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
A4813D
Углы B и C треугольника ABC равны соответственно 61° и 89°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 10.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
64DBE8
Углы B и C треугольника ABC равны соответственно 63° и 87°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 11.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
DC2396
Углы B и C треугольника ABC равны соответственно 62° и 88°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 12.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
FC2D84
Углы B и C треугольника ABC равны соответственно 64° и 86°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 13.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
18FAEE
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
AE3B14
Углы B и C треугольника ABC равны соответственно 66° и 84°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
E5A864
Углы B и C треугольника ABC равны соответственно 67° и 83°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 16.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
CF7752
Углы B и C треугольника ABC равны соответственно 72° и 78°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 17.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
CF802A
Вписанный четырехугольник — это четырехугольник, все вершины которого лежат на одной окружности.
Центр окружности, описанной около четырехугольника — точка пересечения серединных перпендикуляров, проведенных к сторонам четырехугольника.
Признаки вписанного четырехугольника
Для того, чтобы четырехугольник был вписанным, необходимо и достаточно, чтобы выполнялось одно из следующих равенств:
Специальные случаи
Любые квадраты, прямоугольники, равнобедренные трапеции можно вписать в окружность.
Свойства вписанного четырехугольника
- Произведение диагоналей вписанного четырехугольника равняется сумме произведений его противолежащих сторон.
- Диагонали вписанного четырехугольника относятся как суммы, произведений сторон, сходящихся в концах диагоналей.
- Диагонали вписанного четырехугольника разбивают его на две пары подобных треугольников.
- Сумма квадратов противолежащих сторон четырехугольника равна квадрату диаметра описанной окружности.
- Сумма противолежащих углов четырехугольника равна
.
Использование свойств и признаков вписанного четырехугольника при решении геометрических задач.
Задача 1. Высоты и
остроугольного треугольника
пересекаются в точке
. Докажите, что
.
Решение. Рассмотрим четырехугольник .
.
Следовательно, вокруг четырехугольника можно описать окружность и по свойству вписанных углов, опирающихся на одну дугу
.
Рассмотрим четырехугольник .
.
Следовательно, вокруг четырехугольника можно описать окружность и по свойству вписанного четырехугольника
.
— свойство смежных углов.
Следовательно, .
ч.т.д.
Задача 2. В остроугольном треугольнике проведены высоты и
. На них из точек
и
опущены перпендикуляры
и
соответственно. Докажите, что прямые
и
параллельны.
Решение. Рассмотрим четырехугольник .
.
Следовательно, вокруг четырехугольника можно описать окружность и по свойству вписанных углов, опирающихся на одну дугу
.
Рассмотрим четырехугольник .
.
Следовательно, вокруг четырехугольника можно описать окружность и по свойству вписанных углов, опирающихся на одну дугу
.
— соответственные углы, образованные при пересечении прямых
и
секущей
.
Следовательно, прямые и
параллельны.
ч.т.д.