Как найти диагональ четырехугольника
Четырехугольником называется фигура, состоящая из четырех сторон и углов, прилежащих к ним. К числу таких фигур относятся прямоугольник, трапеция, параллелограмм. В ряде задач по геометрии требуется найти диагональ одной из этих фигур.
Инструкция
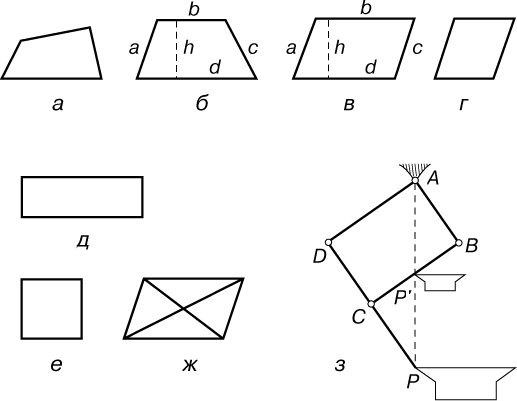
Диагональю четырехугольника называется отрезок, соединяющий его противоположные углы. У четырехугольника имеются две диагонали, которые между собой пересекаются в одной точке. Диагонали иногда бывают равными, как у прямоугольника и квадрата, а иногда имеют различную длину, как, например, у трапеции. Способ нахождения диагонали зависит от фигуры.Постройте прямоугольник со сторонами a и b и двумя диагоналями d1 и d2. Из свойств прямоугольника известно, что его диагонали между собой равны, пересекаются в одной точке и делятся в ней пополам. Если известны две стороны прямоугольника, то его диагонали найдите следующим образом: d1=√a^2+b^2=d2.Частным случаем прямоугольника является квадрат, у которого диагональ равна a√2. Кроме того, диагональ можно найти, зная площадь квадрата. Она равна: S = d^2/2.Отсюда длину диагонали вычислите по формуле: d = √2S.
Несколько иным образом решайте задачу, когда дан не прямоугольник, а параллелограмм. У этой фигуры, в отличие от прямоугольника или квадрата, равны между собой не все углы, а только противоположные. Если в условии задача присутствует параллелограмм со сторонами a и b и заданным между ними углом, как показано на рисунке к шагу, то диагональ найдите, используя теорему косинусов: d^2 = a^2+b^2-2ab*cosα.Параллелограмм, имеющий равные стороны, называется ромбом. Если по условиям задачи необходимо найти диагональ этой фигуры, то потребуются значения его второй диагонали и площади, поскольку диагонали этой фигуры неравны. Формула площади ромба выглядит следующим образом: S = d1*d2/2.Отсюда d2 равна удвоенной площади фигуры, деленной на d1: d2 = 2S/d1.
При вычислении площади трапеции придется воспользоваться тригонометрической функцией синуса. Если данная фигура является равнобочной, то, зная ее первую диагональ d1 и угол между двумя диагоналями AOD, как показано на рисунке к шагу, найдите вторую по следующей формуле: d2 = 2S/d1*sinφ. В данном случае рассматриваем трапецию ABCD.Существует также прямоугольная трапеция, диагональ которой найти несколько проще. Зная длину боковой стороны этой трапеции, совпадающей с ее высотой, а также нижнее основание, найдите ее диагональ, пользуясь обычной теоремой Пифагора. А именно сложите квадраты этих величин, а затем из результата извлеките квадратный корень.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Ученик
(189),
закрыт
6 лет назад
Андрей Маслов
Знаток
(352)
6 лет назад
держи: Четырехугольником называется фигура, состоящая из четырех сторон и углов, прилежащих к ним. К числу таких фигур относятся прямоугольник, трапеция, параллелограмм. В ряде задач по геометрии требуется найти диагональ одной из этих фигур.
Как найти диагональ четырехугольника
Инструкция
1
Диагональю четырехугольника называется отрезок, соединяющий его противоположные углы. У четырехугольника имеются две диагонали, которые между собой пересекаются в одной точке. Диагонали иногда бывают равными, как у прямоугольника и квадрата, а иногда имеют различную длину, как, например, у трапеции. Способ нахождения диагонали зависит от фигуры. Постройте прямоугольник со сторонами a и b и двумя диагоналями d1 и d2. Из свойств прямоугольника известно, что его диагонали между собой равны, пересекаются в одной точке и делятся в ней пополам. Если известны две стороны прямоугольника, то его диагонали найдите следующим образом: d1=√a^2+b^2=d2.Частным случаем прямоугольника является квадрат, у которого диагональ равна a√2. Кроме того, диагональ можно найти, зная площадь квадрата. Она равна: S = d^2/2.Отсюда длину диагонали вычислите по формуле: d = √2S.
2
Несколько иным образом решайте задачу, когда дан не прямоугольник, а параллелограмм. У этой фигуры, в отличие от прямоугольника или квадрата, равны между собой не все углы, а только противоположные. Если в условии задача присутствует параллелограмм со сторонами a и b и заданным между ними углом, как показано на рисунке к шагу, то диагональ найдите, используя теорему косинусов: d^2 = a^2+b^2-2ab*cosα.Параллелограмм, имеющий равные стороны, называется ромбом. Если по условиям задачи необходимо найти диагональ этой фигуры, то потребуются значения его второй диагонали и площади, поскольку диагонали этой фигуры неравны. Формула площади ромба выглядит следующим образом: S = d1*d2/2.Отсюда d2 равна удвоенной площади фигуры, деленной на d1: d2 = 2S/d1.
3
При вычислении площади трапеции придется воспользоваться тригонометрической функцией синуса. Если данная фигура является равнобочной, то, зная ее первую диагональ d1 и угол между двумя диагоналями AOD, как показано на рисунке к шагу, найдите вторую по следующей формуле: d2 = 2S/d1*sinφ. В данном случае рассматриваем трапецию ABCD.Существует также прямоугольная трапеция, диагональ которой найти несколько проще. Зная длину боковой стороны этой трапеции, совпадающей с ее высотой, а также нижнее основание, найдите ее диагональ, пользуясь обычной теоремой Пифагора. А именно сложите квадраты этих величин, а затем из результата извлеките квадратный корень.
Подробнее: http://www.kakprosto.ru/kak-68789-kak-nayti-diagonal-chetyrehugolnika#ixzz4ONs7NCxj
Андванс Чесс
Просветленный
(31696)
6 лет назад
Никак: четырёхугольник – не жёсткая фигура, и длины сторон не определяют длин диагоналей, можно лишь найти диапазоны, в пределах которых длины этих диагоналей находятся. Минимальный размер диагонали определяется максимальной разницей между сторонами, лежащими по одной сторону от диагонали: для диагонали AC минимальная длина больше чем max(|AB-BC|, |AD-DC|) (то есть диапазон значений не включает предельные граничные значения); максимальный размер – минимальной суммой этих сторон.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Диагональ четырёхугольника по сторонам и площади
|
|||
|
Здравствуйте, возникла необходимость найти углы четырёхугольника зная его длины сторон и площадь (такие данные часто есть на плане участков). При поиске по форумам нашёл только формулу как найти диагональ http://forum.dwg.ru/attachment.php?atta … 1278364686 Это позволит гораздо проще найти углы, но моего знания математики забытого школьного уже не очень хватает, чтобы решить это уравнение. Был бы признателен за помощь в решении. Думаю, что многим людям это было бы полезено. Спасибо.
|
||
| Вернуться к началу |
|
||
|
aliakseika |
Заголовок сообщения: Re: Диагональ четырёхугольника по сторонам и площади
|
|
Спасибо, посмотрю в сторону Вольфрам-Альфа
|
|
| Вернуться к началу |
|
|
aliakseika |
Заголовок сообщения: Re: Диагональ четырёхугольника по сторонам и площади
|
|
michel писал(а): Это точно? Не хочется убивать время на то, что не даст корректного результата
|
|
| Вернуться к началу |
|
|
aliakseika |
Заголовок сообщения: Re: Диагональ четырёхугольника по сторонам и площади
|
|
Может вы сможете подсказать формулу правильную? Исходные данные: длины сторон и площадь, надо найти углы этого четырёхугольника. Заранее спасибо!
|
|
| Вернуться к началу |
|
|
Li6-D |
Заголовок сообщения: Re: Диагональ четырёхугольника по сторонам и площади
|
|
Здесь можно обойтись даже циркулем и линейком. Формула на dwg.ru неправильная. Пусть [math]{text{S1}}{text{,}};{text{S2}}[/math] – учетверенные площади двух треугольников со сторонами a,b,x и c,d,x, Поэтому: [math]S{1^2}-S{2^2}= 2{x^2}({a^2}+{b^2}-{c^2}-{d^2})-({a^2}-{b^2}+{c^2}-{d^2})({a^2}-{b^2}-{c^2}+{d^2})[/math] (2).
|
|
| Вернуться к началу |
|
| За это сообщение пользователю Li6-D “Спасибо” сказали: aliakseika |
|
|
dr Watson |
Заголовок сообщения: Re: Диагональ четырёхугольника по сторонам и площади
|
|
Есть ещё вариант. [math]left{begin{matrix}absinalpha_{ab}+cdsinalpha_{cd}=2S\ bcsinalpha_{bc}+adsinalpha_{ad}=2S\ alpha_{ab}+alpha_{bc}+alpha_{cd}+alpha_{da}=2pi\ a^2+b^2-2abcosalpha_{ab}=c^2+d^2-2cdcosalpha_{cd}end{matrix}right.[/math] Здесь [math]a,b,c,d[/math] – последовательные стороны 4-угольника, первые два уравнения из формулы площади треугольника через стороны и угол между ними, третье понятно, четвёртое – теорема косинусов. Один угол исключаем из третьего уравнения, из первых двух выражаем два синуса через другие два линейным образом. Нелинейность (относительно синусов) полезет из третьего с четвёртым …
|
|
| Вернуться к началу |
|
| За это сообщение пользователю dr Watson “Спасибо” сказали: aliakseika |
|
|
aliakseika |
Заголовок сообщения: Re: Диагональ четырёхугольника по сторонам и площади
|
|
Спасибо, оказывается всё не очень тривиально получается. Казалось бы найти углы у четырёхугольника, а на тебе…
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Диагональ четырёхугольника
в форуме Геометрия |
sfanter |
3 |
531 |
20 июл 2014, 07:29 |
|
Диагональ четырехугольника
в форуме Геометрия |
Shuna |
3 |
426 |
22 июл 2014, 15:08 |
|
Площадь четырехугольника по углам и двум сторонам
в форуме Геометрия |
Extraneous |
4 |
534 |
14 июн 2017, 11:38 |
|
Площадь 4угольника по сторонам
в форуме Геометрия |
lady_flute |
3 |
625 |
15 фев 2014, 13:26 |
|
Серединные перпендикуляры к сторонам треугольника
в форуме Геометрия |
sfanter |
3 |
609 |
03 июл 2014, 17:56 |
|
Найти углы трапеции по сторонам
в форуме Геометрия |
mjdoom2 |
4 |
777 |
08 июн 2016, 03:55 |
|
Угол между перпендикулярами к сторонам параллелограмма
в форуме Геометрия |
Doctor_99 |
2 |
1391 |
08 окт 2013, 21:31 |
|
Нахождение углов по трем сторонам треугольника
в форуме Геометрия |
JackLondon |
1 |
308 |
30 авг 2015, 12:24 |
|
Решение прямоугольного треугольника по двум сторонам
в форуме Тригонометрия |
Riko |
8 |
700 |
28 мар 2015, 14:36 |
|
Найти координаты вершины треугольника, по известным сторонам
в форуме Аналитическая геометрия и Векторная алгебра |
Peter2x |
11 |
3435 |
06 апр 2018, 16:33 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: Yandex [bot] и гости: 4 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Посчитать диагональ прямоугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Посчитать диагональ прямоугольника
Чтобы посчитать диагональ прямоугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Посчитать чему равна диагональ (d) любого прямоугольника (в том числе и квадрата) можно зная длины его сторон (a и b).
Просто подставьте их в калькулятор и получите результат.
Чему равна диагональ прямоугольника если сторона
a = ,
а сторона
b = ?
Ответ: d =
0
Теория
Чему равна диагональ прямоугольника d если известны длина стороны a и длина стороны b?
Формула
d = √a2 + b2
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
d = √102 + 52 = √100 + 25 ≈ 11.18 см
См. также
Одна из основных фигур курса математики – прямоугольник.
Впервые о нем заговорили еще в Древнем Египте, а позже и в
Древней Греции. Именно свойства его диагоналей помогают
решить многие задания учебного курса. Подход, который
сейчас используется в геометрии разработал Евклид. Формулы,
представленные в данной статье, пригодятся как при решении
домашних упражнений, так и на ЕГЭ. Именно такие задачки
помогают набрать недостающие баллы, поэтому ими не стоит пренебрегать.
- Диагональ прямоугольника через его стороны
- Диагональ прямоугольника через площадь и известную сторону
- Диагональ прямоугольника через периметр и сторону
- Диагональ прямоугольника через диаметр описанной окружности
- Диагональ прямоугольника через радиус описанной окружности
- Диагональ прямоугольника через площадь и острый угол между диагоналями
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
- Что такое диагональ прямоугольника, когда требуется ее вычисление
Диагональ прямоугольника через его стороны
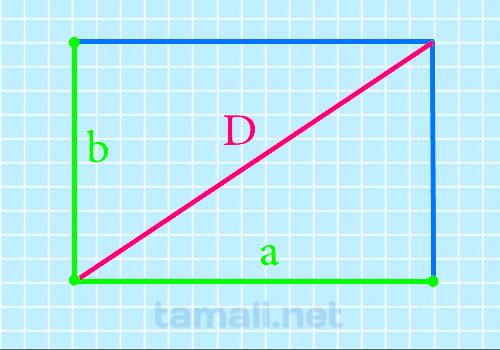
Если заданы хотя бы 2 стороны, то вычислить линию, соединяющую противоположные вершины, будет довольно просто. Применяется классическая теорема Пифагора. Достаточно подставить приведенные в дано числовые параметры в виде суммы квадратов под корнем:
![]()
Где a, b – это стороны, а d – прямая, которую мы ищем.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через площадь и известную сторону
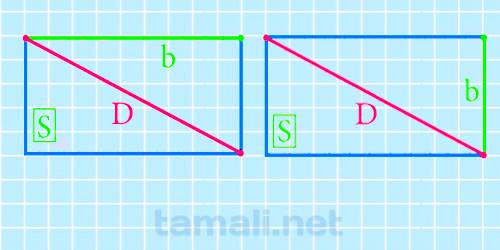
Когда в дано есть S и одна сторона, то узнать искомое значение можно используя следующее равенство:
![]()
Где D – это прямая, которую необходимо найти, a и b – любая заданная сторона, а S – площадь.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через периметр и сторону
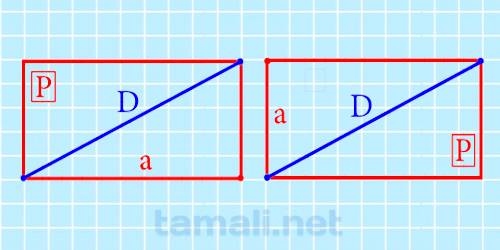
Когда задан периметр (сумма сторон) и, хотя бы одна сторона, отрезок, соединяющий несмежные точки высчитывают так:
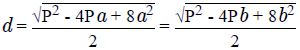
Где P – сумма сторон, a и b – любая заданная сторона.
Рассчитать искомый отрезок можно и через соотношение сторон и площадь.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через диаметр описанной окружности
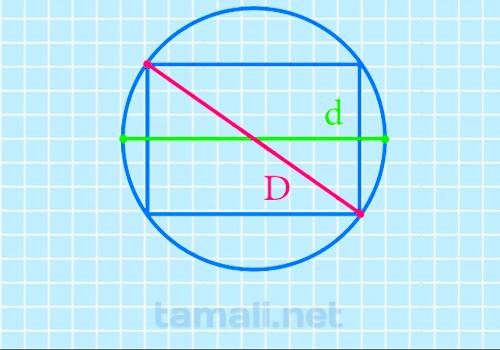
Поиск отрезка через описанную окружность еще более прост, здесь даже не придется проводить расчеты: D = d
Где d – это обозначенный диаметр.
Различить вписанную/описанную окружность легко. Когда геометрическое тело вписано куда-то, то оно всегда будет находиться в другой фигуре. Когда окружность описана, то она находится снаружи, она как бы описывает другое геометрическое тело. Описанные фигуры задевают собой точки, а вписанные – касаются сторон.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через радиус описанной окружности
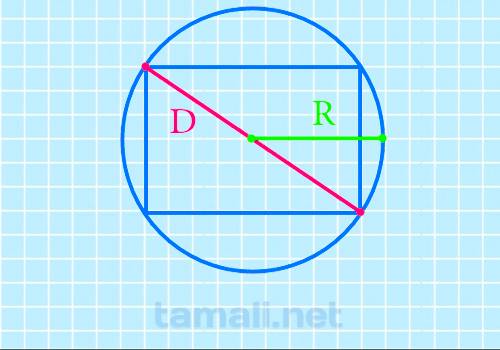
Для расчета искомого отрезка через описанную окружность нужно провести вычисления, где: D = 2R
Где R – это заданный радиус.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через площадь и острый угол между диагоналями
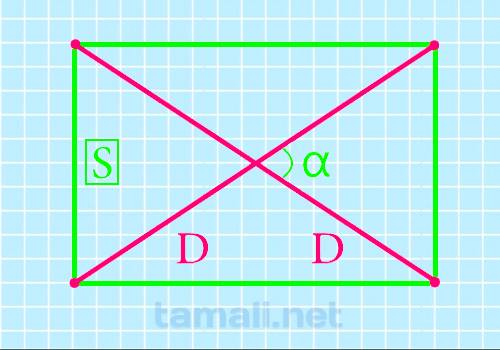
Если необходимо узнать прямую, соединяющую вершины 4-хугольника, это можно осуществить с помощью двух диагоналей. Для получения ответа к задаче понадобится sin β между ними и S (произведение длины и ширины).
Расчет проводится с равенством:
![]()
Где соответственно S – это площадь, а sin β – это острый угол, расположенный внутри фигуры (меж пересекающимися прямыми).
Если в 4-хугольнике расчертить 2 отрезка, объединяющие несмежные вершины, то они будут равны меж собой (все 4 отрезка), а точка пересечения разделит их пополам.
Пересечение всегда происходит в геометрическом центре самой фигурки. Этот же центр является центром описанной окружности.
Площадь (S):
Цифр после запятой:
Результат в:
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
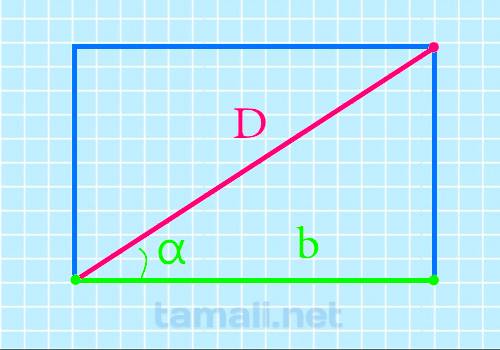
Когда одна из сторон 4-хугольника прилегает к углу, то просчитать отрезок, соединяющий вершины тоже возможно:
![]()
Где b – это сторона, прилегающая к углу, а cos a – это тот самый угол.
Косинус угла в треугольнике с прямым углом рассчитывается по формуле – длина соседней стороны, разделенная на гипотенузу. Синус – это противолежащий катет, разделенный на гипотенузу. Либо можно поступить еще проще, подсмотрев в таблицу Брадиса.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
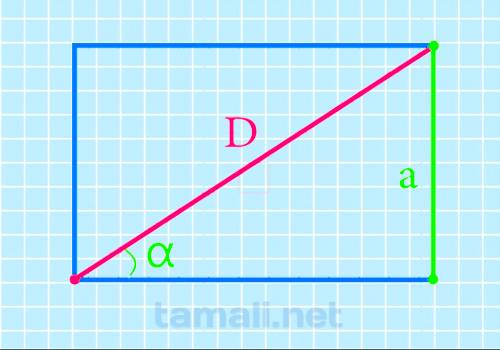
Чтобы найти нужный отрезок внутри четырехугольника, должен быть задан угол, прилегающий к искомому отрезку и сторона, противоположная углу:
![]()
Где a – это сторона четырехугольника, а sin a – это прилегающий угол.
Длинная сторона 4-хугольника– это длина, а короткая – его ширина. Помните, что каждая сторона одновременно является высотой.
Цифр после запятой:
Результат в:
Что такое диагональ прямоугольника, когда требуется ее вычисление
Прямоугольник – это частный случай параллелограмма. Иначе 4-хугольник с попарно равными сторонами, параллельными друг другу, а также равными прямыми углами по 90⁰. Сумма углов четырехугольника составляет 360⁰.
Диагональ разделяет фигуру на два новых элемента – треугольники с прямым углом. Это прямая, объединяющая противоположные вершины. Имея 2 прямоугольных треугольника, отрезок уже можно рассчитать по теореме Пифагора. По теореме гипотенуза – это квадрат из суммы катетов (обозначенных сторон треугольника), возведенных в квадрат.
Линии, соединяющие противоположные точки в четырехугольнике всегда пересекаются друг с другом.
Отрезок обозначают как d или D. Если названы все точки, то его можно называть в соответствии с ними – AC или BD.
Знания о линии, проходящей через несмежные точки 4-хугольника может понадобиться в легких геометрических упражнениях, так и в более сложных многоуровневых задачках, которые появляются на ЕГЭ. Свойства данного отрезка помогают находить важные параметры прямоугольника. Зная данные обеих линий, соединяющих противоположные углы, можно рассчитать S геометрического тела.
Перед решением любой геометрической задачки рекомендуется сделать чертеж и обозначить всю заданную информацию. Так будет значительно проще сосредоточиться на искомом значении.
Если регулярно решать тесты по геометрии, то формулы легче запомнятся, а их применение будет доведено до автоматизма.




