Дельтоид
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Кривцова А.С. 1
1МБОУ СШ №16 г.Павлово Нижегородской области
Захарова Т.Н. 1
1МБОУ СШ №16 г.Павлово Нижегородской области
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
ВВЕДЕНИЕ
На уроках геометрии в первой четверти 8 класса мы изучали различные четырехугольники, такие как параллелограмм, прямоугольник, квадрат, ромб и трапеция. Мы доказывали их свойства и признаки, с помощью которых потом решали различные задачи. Возник вопрос: все ли виды четырехугольников мы изучили? Пытаясь ответить на этот вопрос, в сети Интернет я наткнулась на еще один четырехугольник – дельтоид. Проведя анализ привычных школьных справочников, а также заглянув в знаменитый справочник Бронштейна, я не нашла никаких сведений о дельтоиде. Между тем эту фигуру мы часто встречаем в окружающем мире, например, крона дерева туя (рис.1), тело рыбы (рис.2), человеческий мозжечок (рис.3), соединенные человеческие руки (рис.4), воздушный змей (рис.5), лист дерева (ри.6), а также форма носа и глаза.
рис.1 рис.2 рис.3 рис. 4
рис.5 рис.6
Меня очень заинтересовал данный четырехугольник, и я решила глубже узнать, что это за дельтоид, сформулировать и доказать его свойства и признаки, решить различные задачи с ним, а потом представить свои разработки в виде сайта для своих одноклассников и всех тех, кто интересуется геометрией.
Цель: изучение четырехугольника дельтоид и создание сайта «Все о дельтоиде».
Задачи:
– познакомиться с литературой по данной теме;
– сформулировать различные определения дельтоида;
– сформулировать свойства и признаки дельтоида;
– составить и решить задачи с дельтоидом;
– составить тесты для проверки знаний о дельтоиде;
– создать электронный образовательный ресурс – сайт «Все о дельтоиде», содержащий теоретический и практический материал по данной теме.
Объект исследования: четырехугольник дельтоид.
Предмет исследования: определение, свойства и признаки дельтоида.
Методы исследования: работа с научной литературой, анализ и систематизация теоретического материала, решение задач.
Глава 1. Дельтоид – один из видов четырехугольников
1.1 Определение дельтоида
Дельто́ид (от др.-греч. δελτοειδής — «дельтовидный», напоминающий заглавную букву дельта).
Изучив различную литературу по данной теме, я выделила два определения дельтоида (рис.7):
– Дельтоид – четырёхугольник, у которого есть две пары равных соседних сторон.
– Дельтоид – это четырехугольник, симметричный относительно одной из своих диагоналей. [4,5,6,8]
рис.7
Из определения дельтоида следует, что ромб и квадрат также являются дельтоидами.
Главная диагональ дельтоида – это отрезок, соединяющий вершины неравных углов дельтоида. Неглавной диагональю дельтоида называют вторую диагональ дельтоида.
Средняя линия дельтоида это – отрезок, соединяющий середины соседних сторон дельтоида.
Есть два вида дельтоидов: выпуклый (рис.7) и невыпуклый (рис.8).
рис.8
Все углы выпуклого дельтоида меньше развёрнутого угла, а один из углов невыпуклого дельтоида больше развёрнутого угла.
1.2 Свойства дельтоида
Изучив литературу, по данной теме, мною были выделены следующие свойства дельтоида (табл.1).
Табл.1 Свойства дельтоида
|
1) Углы дельтоида между сторонами разной длины имеют равную величину |
|
|
2) Диагонали дельтоида перпендикулярны друг другу, одна из них делит другую на две равные части |
|
|
3) Во всякий выпуклый дельтоид можно вписать окружность, и только одну |
|
|
4) Неглавная диагональ делит дельтоид на два равнобедренных треугольника |
|
|
5) Главная диагональ дельтоида является биссектрисой противолежащих углов |
|
|
6) Главная диагональ делит дельтоид на два равных треугольника |
|
|
7) Средние линии дельтоида образуют прямоугольник, периметр которого равен сумме диагоналей данного дельтоида |
|
|
8) Площадь дельтоида равна половине произведения диагоналей |
|
|
9) Площадь дельтоида равна произведению двух его неравных сторон на синус угла между ними |
S = absinɸ |
Проведя сравнительный анализ со свойствами изученных четырехугольников, я выделила общие свойства дельтоида, ромба и квадрата:
– диагонали взаимно перпендикулярны;
– площадь равна половине произведения диагоналей;
– средние линии образуют прямоугольник, периметр которого равен сумме диагоналей данного дельтоида.
Также в любой выпуклый дельтоид, как и в квадрат, можно вписать окружность, и только одну.
Мною были определены и различия в свойствах дельтоида и других изученных четырехугольников. У дельтоида:
– только одна пара равных противолежащих углов (у параллелограмма, прямоугольника, ромба, квадрата – две);
– только одна диагональ точкой пересечения диагоналей делится пополам (у параллелограмма, прямоугольника, ромба, квадрата – обе диагонали);
– только главная диагональ делит на два равных треугольника (у параллелограмма, прямоугольника, ромба, квадрата – обе диагонали);
– только главная диагональ дельтоида является биссектрисой противолежащих углов (у ромба – обе диагонали);
– только неглавная диагональ делит дельтоид на два равнобедренных треугольника (у квадрата и ромба – обе диагонали).
1.3 Признаки дельтоида
Можно выделить четыре признака дельтоида (табл.2).
Табл.2 Признаки дельтоида
|
1)Если у четырёхугольника только одна ось симметрии, проходящая через диагональ, то это дельтоид |
|
|
2) Если четырёхугольник образован двумя равнобедренными треугольниками с разными боковыми сторонами и общим основанием, то это дельтоид |
|
|
3) Если у четырехугольника диагонали взаимно перпендикулярны и только одна из них делит другую пополам, то это дельтоид |
|
|
4) Если в четырёхугольнике только одна диагональ является биссектрисой противоположных углов, то это дельтоид |
1.4 Задачи с дельтоидом
Изучив некоторые российские учебные пособия по математике [1], я не встретила системы задач про дельтоид. Однако мы встречались с этой геометрической фигурой на уроках геометрии еще в 7 классе (УМК по ред. А.Г.Мерзляка [2,3]), когда решали задачи на применение признаков равенства треугольников (№161 (рис.9), №176 (рис.10)) и задачи по теме «Касательная к окружности» (№523 (рис.11)).
рис.9 рис.10 рис.11
Изучив признаки и свойства дельтоида, я попыталась составить достаточное количество разнообразных и интересных задач с дельтоидом вычислительного характера. Примеры таких задач приведены ниже, для некоторых из них рассмотрено решение. [7]
Задача 1
Одна из диагоналей дельтоида равна 16 см, а его площадь – 120 см2. Чему равна длина второй диагонали дельтоида?
Решение.
S = d1d2
120 = ·16· d2; 120 = 8· d2; d2 = 120 : 8; d2 = 15 см
Ответ: 15 см
Задача 2
|
Найти стороны дельтоида, если его периметр равен 116 см, а разность боковых сторон равна 3 см. Решение (рис.12): Р=2(АВ + AD) 2(х+3+х)=116 |
рис.12 |
2(2х+3)=116
4х+6=116
4х=110
х=27,5
DC=AD=27,5 см
АВ=ВС=27,5+3=30,5 см
Ответ: АВ=30,5 см; ВС=30,5 см; CD=27,5 см; AD=27,5 см
Задача 3
|
На сторонах АВ и ВС прямоугольника АВСD взяты точки К и О соответственно так, что КВ = ВО, а на стороне АD взята точка Е так, что КЕ = ОЕ. Найти АВЕ. Решение (рис.13): 1)В = 90°, так как АВСD – прямоугольник. 2)Рассмотрим четырёхугольник КВОЕ. КВ=ОВ (по условию); КЕ=ОЕ (по условию). Значит, КВОЕ – дельтоид по определению. |
р ис.13 |
3)ВЕ – главная диагональ дельтоида, следовательно, она является биссектрисой противолежащих углов дельтоида, т.е. АВЕ= В. Значит, АВЕ= · 90° = 45°.
Ответ: АВЕ=45°
Задача 4
|
На сторонах АВ, ВС и АС треугольника АВС отмечены точки F, D и E такие, что ЕС : АЕ = 2 : 1, FЕ = DЕ, АF = 2 см, DС = 5 см, FВ = ВD. Найдите FВ. Решение (рис.14): 1) Так как FE = DE, FB = BD по условию, то BDEF – дельтоид по определению. |
рис.14 |
2) BE – главная диагональ дельтоида, а, значит, и биссектриса B (по свойству дельтоида).
По свойству биссектрисы или .
Пусть FB = BD=х, тогда
2(х+2)=х+5
2х+4=х+5
х=1
FB = BD = 1 см
Ответ: FB = 1 см
Задача 5
Равные стороны АВ и ВС дельтоида АВСD перпендикулярны и равны
2 см, К – точка пересечения диагоналей АС и ВD, АК = КС. Из точки К проведен перпендикуляр КЕ к стороне СD, СЕ = 1 см. Найдите ЕD.
|
Решение (рис.15): ∆ ABC – равнобедренный прямоугольный треугольник, т.к. AB = BC и АВ ВС. По теореме Пифагора + = , AC = 4 см |
2) Т.К. АК = КС по условию, то АК = КС = 2 см. рис.15
3) AC BD по свойству дельтоида, значит, ∆ KCD – прямоугольный.
КС² = CE ∙ CD (по теореме о пропорциональных отрезках в прямоугольном треугольнике)
2²=1 ∙ (1 + ED)
4=1 + ED
ED = 3 см
Ответ: ED = 3 см
1.5 Тесты по теме «Дельтоид»
Рассмотрев свойства и признаки дельтоида, изучив возможность их применения для решения задач, я составила тесты для проверки знаний по теме «Дельтоид».
Обобщающий тест «Всё о дельтоиде»
Форму какого из четырехугольников имеет мозжечок человека:
Ромб
Прямоугольник
Дельтоид
Трапеция
Ответ: 3
Выберите верное утверждение:
Дельтоид – это четырехугольник, у которого стороны попарно равны
Дельтоид – это четырехугольник, у которого есть две пары равных соседних сторон
Дельтоид – это четырехугольник, у которого диагонали взаимно перпендикулярны
Дельтоид – это четырехугольник, у которого две стороны равны
Ответ: 2
Выберите неверное утверждение:
Главная диагональ дельтоида – это отрезок, соединяющий вершины неравных углов дельтоида
Дельтоид – это четырехугольник, в котором две пары соседних сторон равны
Неглавная диагональ дельтоида – это отрезок, соединяющий вершины равных углов дельтоида
Средняя линия дельтоида – это отрезок, соединяющий стороны дельтоида
Ответ: 4
Какой четырехугольник может быть невыпуклым:
Ромб
Трапеция
Дельтоид
Параллелограмм
Ответ: 3
Выберите верное утверждение:
Если в четырехугольнике две стороны равны, то это дельтоид
Если четырехугольник образован двумя равнобедренными треугольниками с разными боковыми сторонами и общим основанием, то это дельтоид
Если в четырехугольнике диагонали является биссектрисами противолежащих углов, то это дельтоид
Если в четырехугольнике есть пара равных соседних сторон, то это дельтоид
Ответ: 2
Выберите неверное утверждение:
Все углы дельтоида равны
Углы дельтоида между сторонами разной длины имеют равную величину
Площадь дельтоида равна половине произведения его диагоналей
Главная диагональ делит дельтоид на два равных треугольника
Ответ: 1
Выберите верное утверждение:
Около всякого выпуклого дельтоида можно описать окружность
Все стороны дельтоида равны
Неглавная диагональ делит дельтоид на два равнобедренных треугольника
В выпуклом дельтоиде один из углов больше развёрнутого
Ответ: 3
У какого четырехугольника только одна диагональ является биссектрисой противолежащих углов:
Квадрат
Ромб
Прямоугольник
Дельтоид
Ответ: 4
В дельтоиде смежные стороны относятся как 3 : 5. Найдите большую сторону дельтоида, если его периметр равен 48 см.
15 см
3 см
9 см
30 см
Ответ: 1
Одна из диагоналей дельтоида равна 18 см, а его площадь – 234 см2. Чему равна длина второй диагонали дельтоида?
13 см
26 см
450 см
99 см
Ответ: 2
Какого из перечисленных элементов нет у дельтоида?
Диагональ
Угол
Радиус описанной окружности
Радиус вписанной окружности
Ответ: 3
АВСD – дельтоид. Треугольник АВС равносторонний, и его периметр равен 30 см. Треугольник АСD – равнобедренный, и его периметр равен 46 см. Найдите периметр дельтоида АВСD.
76 см
18 см
180 см
56 см
Ответ: 4
1.6 Создание электронного образовательного ресурса – сайт «Все о дельтоиде»
Проделав работу по формулированию и доказательству свойств и признаков дельтоида, составлению и решению задач на вычисление различных величин в дельтоиде, созданию тестов по теме «Дельтоид», весь разработанный материал я оформила в виде сайта «Все о дельтоиде», размещенного по адресу https://sites.google.com/view/deltoid-na5.
Данный сайт можно использовать для объяснения материала о дельтоиде на уроках геометрии и во внеурочной деятельности, для самостоятельного изучения обучающимися этой темы с последующей проверкой полученных знаний в ходе решения интерактивных тестов.
Данный сайт состоит из шести разделов:
1 раздел – Главная страница (рис. 16) – содержит общую информацию о создателе сайта, а также рассмотрены примеры дельтоидов из окружающей обстановки.
рис.16
2 раздел – «Что такое дельтоид» (рис.17), в котором приведены различные определения дельтоида, рассмотрены его элементы.
рис.17
3 и 4 разделы – «Свойства дельтоида» и «Признаки дельтоида» (рис.18. рис.19). В этих разделах сформулированы характерные для дельтоида свойства и признаки.
рис.18 рис.19
5 раздел – «Задачи и дельтоидом» (рис.20). На этой странице приведены решения некоторых задач на вычисление различных элементов дельтоида, а также предложены задачи для самостоятельного решения.
рис.20
6 раздел – «Тесты по теме «Дельтоид» (рис.21, рис.22). В этом разделе можно проверить свои знания по данной теме с помощью предложенных интерактивных тестов.
рис.21 рис.22
На одном из уроков геометрии я предложила своим одноклассникам познакомиться с дельтоидом, изучив материал на сайте «Все о дельтоиде» (рис.23, рис.24, рис. 25).
рис.23 рис.24 рис.25
Мне было очень интересно узнать мнение ребят о моем электронном образовательном ресурсе – сайте «Все о дельтоиде». Вот некоторые из высказываний.
Таня Т.: «Очень интересно было узнать об еще одном четырехугольнике – дельтоиде».
Оля П.: «Информация изложена доступно и понятно. Понравилось самостоятельно решать задачи с дельтоидом».
Антон Р.: «Оказывается, что дельтоид окружает нас повсюду».
Настя К.: «Изучив определение, свойства и признаки дельтоида и решив задачи для самостоятельной работы, я практически без ошибок прошла интерактивное тестирование».
Заключение
В данной работе изучена неизвестная в школьном курсе математики геометрическая фигура – дельтоид, которая, однако, встречается очень часто в нашей жизни. Была проделана работа по формулированию свойств и признаков этого четырехугольника, составлено достаточное количество разнообразных задач на вычисление различных элементов дельтоида, также были разработаны тесты для оценки знаний по данной теме. Весь накопленный материал я оформила в виде электронного образовательного ресурса – сайта «Все о дельтоиде», который был предложен моим одноклассникам на одном из уроков геометрии и получил положительные отзывы.
Таким образом, цели, стоящей перед нами, мы достигли – изучен четырехугольник дельтоид. Я бы порекомендовала использовать созданный электронный продукт на урочной и внеурочной деятельности для объяснения материала по данной теме, самостоятельного изучения обучающимися этой темы с последующей проверкой полученных знаний в ходе выполнения интерактивных тестов.
Литература
Киселев А.П. Геометрия / Под ред. Н.А.Глаголева.-М.:ФИЗМАТЛИТ,2013.-328с.
Мерзляк А.Г., Полонский В.Б., Якир М.С. и др. Геометрия 7 класс: учеб. для общеобразоват. организаций.- М.: Вентана-Граф, 2017
Мерзляк А.Г., Полонский В.Б., Якир М.С. и др. Геометрия 8 класс: учеб. для общеобразоват. организаций.- М.: Вентана-Граф, 2018
Перельман Я.И. Занимательная алгебра, геометрия. М.: Книга, 2005
Титаренко А.М., Роганин А.Н. Новейший полный справочник школьника:5-11 классы.-М.:Эксмо, 2008.-304с.
Цыпкин А.Г. Справочник по математике для средней школы.-М.: Наука. Главная редакция физико-математической литературы, 1981.-400с.
Шноль Д, Сгибнев А, Нетрусова Н. Система открытых задач по геометрии: 8 класс – М.: Чистые пруды, 2009. – 32 с.: ил. – (Библиотечка «Первого сентября», серия «Математика». Вып. 29).
Энциклопедический словарь юного математика / Сост. А.П.Савин. -М.:Педагогика,1989.-352с.
http://math4school.ru/chetyrehugolniki.html
http://www.resolventa.ru/
https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D0%BB%D1%8C%D1%82%D0%BE%D0%B8%D0%B4
Просмотров работы: 5496
МУНИЦИПАЛЬНЫЙ ЭТАП РЕСПУБЛИКАНСКОГО КОНКУРСА-ЗАЩИТЫ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИХ РАБОТ МАН «ИСКАТЕЛЬ»
Математическое отделение
Секция
«Прикладная математика»
Базовая
дисциплина «Математика»
Дельтоид
Работу выполнил:
Данилов Даниил,
обучающийся 9 класса
МБОУ «Сакская СШ № 3 им. кавалера
Ордена Славы 3-х степеней
И.И. Морозова»
Научный руководитель:
Речицкая Розалия Леонидовна,
учитель математики
МБОУ
«Сакская СШ №3 им. кавалера
Ордена Славы 3-х степеней
И.И. Морозова»
2022 г.
СОДЕРЖАНИЕ
Введение…………………………………………………………………….3
Глоссарий…………………………………………………………………..4
Раздел
1. История изучения……………………………………………….5
Раздел 2. Свойства дельтоида……………………………………………..6
Раздел
3. Признаки дельтоида……………………………………………..10
Раздел
4. Дельтоид и окружность ………………………………………..12
Раздел 5. Задачи с
дельтоидом……………………………………………15
Раздел
6. Тест «Знаешь ли ты дельтоид ?»……………………………….19
Раздел
7. Дельтоид в окружающем мире ……………………………… 22
Заключение…………………………………………………………………23
Список литературы………………………………………………………..24
Введение
На уроках геометрии мы изучаем такие четырёхугольники, как
параллелограмм, его частные случаи – прямоугольник, ромб и квадрат, кроме них
трапецию. На уроках мы доказывали их свойства и признаки, решали задачи по
нахождению элементов этих четырёхугольников с помощью свойств и признаков.
На одном из таких уроков мы изучали ромб, и учитель дал нам
задание начертить данную фигуру. Один из моих одноклассников допустил ошибку
при построении ромба. Увидев его неправильно построенный ромб, преподаватель
сказала нам, что такая фигура существует, и называется она дельтоид.
Меня заинтересовала данная фигура, и я решил найти материал и
создать на данную тему исследовательскую работу.
Цель данной исследовательской работы – познакомиться с новой
геометрической фигурой дельтоид, его признаками и свойствами, доказать их,
решить задачи о дельтоиде и составить тест тренажер для проверки знаний о
дельтоиде.
Задачи, которые стояли при реализации этой работы:
·
Сформулировать и доказать свойства
и признаки дельтоида.
·
Составить и решить задача о дельтоиде.
·
Продемонстрировать наличие
дельтоидов в окружающем нас мире.
·
Составить
тест на основе материала о дельтоиде.
Глоссарий
Дельтоид – четырёхугольник, у которого
есть две пары равных смежных
сторон.
Главная диагональ дельтоида – это отрезок, соединяющий вершины неравных углов
дельтоида.
Неглавной диагональю дельтоида назовем вторую диагональ дельтоида.
Средняя линия дельтоида это – отрезок, соединяющий середины смежных сторон дельтоида.
Гармонический
четырехугольник – вписанный четырехугольник с перпендикулярными
диагоналями, произведение длин противоположенных сторон которого равны.
Раздел 1. История изучения.
Леонард
Эйлер впервые упоминает настоящую дельтоиду в 1745 году в связи с задачей из
оптики.
Название
кривая получила за сходство с греческой буквой Δ. Её свойства
впервые изучались Леонардом Эйлером (Рис. 1.1) в XVIII веке, а затем Якобом Штейнером (Рис.1.2) в XIX веке.
Рис. 1.1
Рис. 1.2
Раздел
2. Свойства дельтоида
Виды дельтоидов:
![]()
 Есть два вида дельтоидов: выпуклый
Есть два вида дельтоидов: выпуклый
и невыпуклый. Все углы выпуклого
дельтоида меньше развёрнутого угла, а один из углов невыпуклого дельтоида больше развёрнутого угла.
Сформулируем и докажем
несколько свойств дельтоида.
Свойство 1:
![]()
 Углы
Углы
дельтоида между сторонами разной длины имеют равную величину.
Доказательство:
Рассмотрим треугольники ABC и ADC. Сторона AC у них общая. Стороны
AB и AD равны, стороны
BC и CD равны
![]() по условию.
по условию.
Значит, по третьему
признаку равенства
треугольников треугольники ABC
и ADC равны. Из этого следует, что угол ABC
равен углу ADC, что
и требовалось доказать.
Свойство 2:
Главная диагональ дельтоида является биссектрисой противолежащих углов.
 Доказательство:
Доказательство:
Из доказательства первого
свойства
Следует, что треугольники ABC и
ADC равны. Значит, углы BAC и DAC, BCA и DCA попарно
равны. Следовательно,
![]() диагональ AC является биссектрисой, что и требовалось доказать.
диагональ AC является биссектрисой, что и требовалось доказать.

Свойство 3:
Диагонали дельтоида перпендикулярны друг другу, одна
из них делит другую на две равные
части.
![]() Доказательство:
Доказательство:
Рассмотрим треугольник ABD. Он
является равнобедренным по условию.
 Из этого мы можем сделать вывод, что биссектриса угла А,
Из этого мы можем сделать вывод, что биссектриса угла А,
проведённая к основанию треугольника, является ещё и высотой, и медианой.
Следовательно, отрезки OD и BO равны,
а диагонали BD и AС перпендикулярны, то есть
диагонали перпендикулярны, а одна из них делится
точкой пересечения пополам, что и требовалось доказать.
Свойство 4:
Во всякий выпуклый
дельтоид
можно вписать окружность, и только одну.
Доказательство:
 Известно, что если суммы длин противоположных сторон
Известно, что если суммы длин противоположных сторон
выпуклого четырехугольника
равны, то в него можно вписать
окружность.
По определению выпуклого дельтоида он имеет
 две пары равных смежных сторон. Значит, сумма сторон АВ и
две пары равных смежных сторон. Значит, сумма сторон АВ и
DC равна сумме сторон AD и ВС.
![]() Следовательно, в дельтоид
Следовательно, в дельтоид
можно вписать единственную окружность, что и требовалось доказать. Свойство
5:
 Неглавная диагональ делит дельтоид на два равнобедренных треугольника.
Неглавная диагональ делит дельтоид на два равнобедренных треугольника.
Доказательство:
Из определения дельтоида следует, что треугольники ABD и BCD равнобедренные.
![]() Свойство 6:
Свойство 6:
Главная диагональ делит дельтоид
на два равных треугольника.
Доказательство: Равенство треугольников доказано в 1 свойстве.
 Свойство 7:
Свойство 7:
Средние линии дельтоида образуют прямоугольник, периметр которого равен сумме
диагоналей данного дельтоида.
Доказательство:
![]() Дано: ABCD
Дано: ABCD
– дельтоид, точки L,
E, F, M – середины
сторон (BD=DC, CE=ED, DF=FA, BM=MA)
Доказать: MLEF – прямоугольник.
Периметр прямоугольника MLEF равен сумме СА и
ВD.
Доказательство:
Сторона MF параллельна BD
и LE параллельна DB, как средние линии треугольников, т. е. MF параллельна LE.
Аналогично сторона
ML параллельна CA
и EF параллельна CA, т. е. ML
параллельна EF. Значит,
MLEF – параллелограмм.
Диагональ СА перпендикулярна
ВD, значит, и ML, и ЕF перпендикулярна MF и
LE, отсюда следует,
что прямоугольник, и сумма ML
и ЕF равна СА и сумма MF и LE равна ВD.
Следовательно, ML+ ЕF+ MF+ LE= СА + ВD, что и требовалось доказать.
 Свойство 8:
Свойство 8:
Площадь дельтоида равна половине произведения диагоналей.
Доказательство:
Рассмотрим равнобедренный треугольник
DAB, АО – высота в нём.
![]() Площадь треугольника равна
Площадь треугольника равна
половине произведения основания на
высоту. Рассмотрим равнобедренный
треугольник BCD, СО – высота в нём.
Площадь треугольника равна
произведению высоты на половину основания. Площадь
дельтоида ABCD равна сумме площадей треугольников BAD и BCD, а значит, что площадь дельтоида равна
половине произведения диагоналей, что
и следовало доказать.
Раздел 3. Признаки дельтоида
Признак 1:
Если
у четырёхугольника только одна ось симметрии, проходящая через диагональ, то это дельтоид.
Доказательство:
Рассмотрим два треугольника ABC и ADC
В них угол B равен углу D в
силу симметрии. Сторона AC у них – общая.
 |
Значит, треугольники
равны по первому признаку равенства треугольников. Из этого можно
сделать вывод, что сторона AD и сторона AB равны.
![]()
Аналогично доказываем и равенство AOD и COD.
Из это следует, что стороны
DC и BC равны (смежные
стороны) Из всего
вышесказанного следует, что это
дельтоид,
что и требовалось доказать.
Признак 2:
Если
четырёхугольник образован двумя равнобедренными треугольниками с разными боковыми
сторонами и общим основанием, то это дельтоид.

Доказательство:
Из определения о дельтоиде мы знаем, что дельтоид имеет только 2 пары
смежных.
![]() Сторона DA равна стороне AB, и
Сторона DA равна стороне AB, и
они
смежные, сторона DC
равна
стороне СВ, и они смежные,
из этого можно сделать вывод, что это
дельтоид, что и требовалось доказать.
Признак 3:
Если
у четырехугольника диагонали
взаимно перпендикулярны и одна делит другую пополам,
то это дельтоид.
 Доказательство:
Доказательство:
Треугольники ABD и CBD – равнобедренные,
так как их медианы являются
высотами по условию.
Из всего выше сказанного следует,
![]() что это дельтоид, что и требовалось доказать.
что это дельтоид, что и требовалось доказать.
Признак 4:
Если в четырёхугольнике только
одна диагональ является
биссектрисой противоположных
углов, то это дельтоид.
Доказательство:
Рассмотрим треугольники ABC и ADC. Они равны по общей
стороне AC и двум углам, равным по условию теоремы о том, что диагональ – биссектриса.
Из этого можно сделать вывод, что это дельтоид, что и
требовалось доказать.
Раздел
4. Дельтоид и окружность
Теорема. Если у четырехугольна, вписанного в окружность, ось
симметрии совпадает с диагональю, то он является дельтоидом.
 Рис. 4.1
Рис. 4.1
Дано: ABCD – четырехугольник, окружность (O, R) –
описанная, BD – диагональ = ось симметрии
Доказать: ABCD – дельтоид
Доказательство: Т.к. BD – ось симметрии, то A-C,
значит AC-BD
∆ABE = ∆CBE (по 1 признаку: AE=CE, BE –
общая, /BEA=/BEC=90), значит AB=BC , ∆AED = ∆CED (по 1 признаку: AE=CE, DE
– общая, /AED=/CED=90), значит, AD=CD. Поэтому ABCD – дельтоид.
Площадь вписанного дельтоида можно найти
другим способом. Докажем теорему: если дельтоид со сторонами a,
b, вписан в окружность радиуса R, то его площадь равна
![]()
Доказательство: рис.4.2
Пусть диагонали
дельтоида равны x и y.
SABCD =
SABC + SACD или SABCD = SBCD + SABD.
Воспользовавшись
формулой S= abc/4R, где a,b,c, – стороны треугольника, а R- радиус описанной
окружности, получаем:
SABCD =
aby/2R (1) или SABCD = a 2y/4R+ b
2y/4R (2)
Перемножив неравенства (1) и (2), получаем:
SABCD =
abx/2R*(a 2y/4R+ b 2y/4R) = 1/8R2* ab(a2+b2)
* xy = 1/8R2* 2a2b2 (a2 + b2)
= 1/4R2* a 2b 2(a2 + b2)
(так как по теореме Птолемея xy = ac+bd, то
есть xy = 2ab), значит S
= ![]() .
.
Докажем, что в
дельтоид можно вписать окружность.
Доказательство: В
четырехугольник можно вписать окружность, если суммы противолежащих сторон
равны. Действительно, т.к. AB=BC и CD=AD, то AB+CD=BC+AD.
Теорема.
Вписанный дельтоид является примером гармонического
четырехугольника.
Вписанный в окружность четырехугольник обладает рядом интереснейших
свойств. Одно из них было доказано древнегреческим математиком и астрономом
Клавдием Птолемеем (около 100 – 178 г. н. э.) в его знаменитом сочинении
«Альмагест» (астрономы в странах арабского Востока называли эту книгу
«Альмаджисти» – «Величайшие», отсюда и происходит её название «Альмагест»).
Теорема, носящая имя
Птолемея: произведение диагоналей вписанного четырехугольника равно
сумме произведений его противоположных сторон.
Т.к. у дельтоида две
пары равных соседних сторон, то утверждение выглядит так: d1*d2=2a*b
Докажем это:
рис.4.3 
.
Возьмём на диагонали
AC точку E так, что <ABE = <DBC. Тогда ∆ABE и ∆DBC подобны,
т.к. <BAE = <BAC= <BDC. Поэтому ![]() , т.е. AB*DC = AE*DB.
, т.е. AB*DC = AE*DB.
(1) Ясно также, что <CBE = <DBA (т.к. <CBE = <DBC
+ <DBE (по условию)), а значит, ∆CBE и ∆DBA подобны, т.к. <BCE
= <BDA (опираются на одну дугу), поэтому ![]() , то есть CB*DA = CE*DB (2).
, то есть CB*DA = CE*DB (2).
Сложив полученные неравенства (1) и (2), получим: AB*DC + CB*DA = AE*DB + CE*DB
= DB*(AE + CE) = BD*AC,
то есть d1*d2 =
2a*b
Теорема доказана.
Теорема.
Сумма квадратов
неравных сторон равна учетверённому квадрату радиуса описанной окружности.
Рассмотрим вписанный
в окружность четырехугольник ABCD, диагонали которого перпендикулярны. В нём
AB=a, BC=b, CD=c, AD=d, а радиус описанной окружности равен R.
Докажем, что
![]() .
.
Пусть BD = d1, AC
= d2, <ABD =<1, < BAC =<2, < CAD =<3, <
ADB= <4, тогда <BCA= <4 ( т.к. опираются с < ADB на одну
дугу), аналогично <BCA= < 4, < CBD= <3, <BDC= <2,
< ACD= <1. По теореме синусов получаем:
b/sin<1=a/sin<2=2R, отсюда, a = 2R*sin <2, b = 2R*sin <1(так как <2 = 900 – <1), из этого a2 + b2 = 4R2 sin <1 + 4R2 cos /<2=
4R2, следовательно, a2 + b2 =
4R2
Свойство доказано.
Раздел 5.
Задачи с дельтоидом
Задача 1:


 Найти площадь дельтоида ABCD. Дано:
Найти площадь дельтоида ABCD. Дано:
ABCD – дельтоид Стороны
AB и AD равны
Сторона BC равна стороне CD Сторона AB равна
20 см Сторона BC больше AB в 2 раза. Треугольник ABC
![]() Периметр ABC равен 110 см.
Периметр ABC равен 110 см.
Периметр ABD равен 70 см.
Найти:
Площадь дельтоида ABCD
Решение:
DC = BC = 20×2=40
AC =110-(40+20)
=50(см)
BD = 70-(20×2) =30(см) SABCD=0,5×50×30= 750(см2)
Ответ: SABCD =750 см2
Задача 2:
 Дан дельтоид ABCD. Одна его диагональ равна
Дан дельтоид ABCD. Одна его диагональ равна
18 см,
площадь равна
126 см2.
Найдите длину второй диагонали. Найти:
Диагональ AC
.
Решение:
![]() S=0,5×BD×AC; 126=0,5×18×AC
S=0,5×BD×AC; 126=0,5×18×AC
AC= 126 : 18 : 0,5 = 14
Ответ: диагональ AC равна 14 см.
Задача 3:
 Если одна сторона
Если одна сторона
дельтоида в два раза больше
другой.
Периметр дельтоида равен 120 см.
Найдите его стороны.
Решение:
Если одна сторона
дельтоида-x, то вторая – 2x.
Составим уравнение:
![]() 2× (x+2x) =120
2× (x+2x) =120
6x=120 x=120/6 x=20
Если x равен 20 см, то вторая
сторона равна x×2=40
Ответ: стороны равны 20 см и
40 см.

 Задача 4:
Задача 4:
![]() Дано:
Дано:
BCDA-дельтоид PABD= 45
PBCD =55
![]() Треугольник ABD равносторонний Треугольник BCD равнобедренный
Треугольник ABD равносторонний Треугольник BCD равнобедренный
Найти:
периметр дельтоида ABCD.
Решение:
Стороны AB, BD и AD, они равны 45:3=15. Если сторона BD равна 15, то (55-15): 2=20 из этого следует, что AD=15, AB=15, BC=20, CD=20 PABCD = 2× (15+20) = 70
Ответ: периметр дельтоида ABCD равен
70.
 Задача 5:
Задача 5:
![]()
![]()
![]() Одна сторона на 3 см меньше противолежащей.
Одна сторона на 3 см меньше противолежащей.
Периметр ABCD равен
18 см.
Найти все стороны.
Решение:
![]() Пусть х это сторона АВ, тогда (х+3) – это сторона
Пусть х это сторона АВ, тогда (х+3) – это сторона
CD, составим уравнение:
2× (х+(х+3)) =18; 4х= 12; х=3 см; АВ=3 см; АВ=AD
AD=3 см; BC=х+3; BC=6 см; BC=СD; СD=6 см.
Ответ: Стороны AВ и AD равны 3 см,
стороны ВС и CD равны
6 см.
 Задача 6:
Задача 6:
Один угол больше соседнего на 40̊,
а противолежащий = 10̊.
Найти все углы.
Решение:
Пусть х – это угол 1,
тогда (х+40) угол 2 и угол 4,
а угол 3 равен (360 – (х +2× (х+40)),
![]() составим уравнение:
составим уравнение:
х+2×(х+40) +10=360 3х+90=360
3х=270 х=90
Если угол 1 равен 90 градусам, то Угол 2 равен 90+40=130 градусам.
Угол 3 равен 10 градусам.
(по условию)
Угол 4 равен 90+40=130 градусам. (как
противолежащий) Ответ: угол 1 – 90̊, угол 2 – 130̊, угол 3 –
10̊, угол 4 – 130̊.
Раздел 6. Тест «Знаешь ли ты дельтоид?»
|
Вопрос № 1 Выбери правильное утверждение. |
|
|
|
Если в четырёхугольнике есть пара смежных сторон, то это дельтоид. |
|
|
Если в четырехугольнике |
|
|
Если в четырёхугольнике две стороны равны, |
|
|
Если четырёхугольник образован двумя равнобедренными треугольниками, то это дельтоид. |
Вопрос № 2
|
В дельтоиде смежные стороны |
|
|
|
5 |
|
|
6 |
|
|
8 |
|
|
3 |
Вопрос № 3
|
BCDA-дельтоид. |
|
|
|
60 |
|
|
50 |
|
|
55 |
|
|
80 |
Вопрос № 4
|
Дан дельтоид ABCD. |
|
|
|
7 |
|
|
8 |
|
|
9 |
|
|
6 |
Вопрос № 5
|
Выбери неверное утверждение: |
||
|
|
Дельтоид — четырёхугольник, в котором две |
|
|
|
Главная диагональ дельтоида |
|
|
|
Средняя линия дельтоида это – линия, |
|
|
|
Неглавной вершины. |
|
Вопрос № 6
|
Выбери верное утверждение: |
|
|
|
Существует пять видов дельтоидов. |
|
|
В выпуклом дельтоиде все углы меньше развёрнутого. |
|
|
В невыпуклом дельтоиде несколько развёрнутых углов. |
|
|
Углы дельтоида имеют |
Вопрос № 7
|
Выберите определение дельтоида: |
|
|
|
Дельтоид – это четырёхугольник, у которого стороны |
|
|
Дельтоид – это четырёхугольник, у которого смежные стороны попарно равны. |
|
|
Дельтоид – это четырёхугольник, у которого диагонали взаимно перпендикулярны. |
|
|
Дельтоид – это четырёхугольник, |
Вопрос № 8
|
Выберите |
|
|
|
Трапеция |
|
|
Ромб |
|
|
Дельтоид |
|
|
Прямоугольник |
Вопрос № 9
|
Как называется четырёхугольник, |
|
|
|
Трапеция |
|
|
Дельтоид |
|
|
Прямоугольник |
|
|
Ромб |
Вопрос
№ 10
|
Форму какого из перечисленных четырёхугольников имеет монитор компьютера? |
|
|
|
Дельтоид |
|
|
Ромб |
|
|
Прямоугольник |
|
|
Трапеция |
Вопрос
№ 11
|
Выберите |
||
|
|
Трапеция |
|
|
|
Дельтоид |
|
|
|
Ромб |
|
|
|
Прямоугольник |
|
Вопрос № 12
|
Какого из |
|
|
|
Угол |
|
|
Радиус описанной окружности |
|
|
Диагональ |
|
|
Радиус вписанной окружности |
Раздел 7. Дельтоид среди нас.
Дельтоид очень часто встречается в
окружающем нас мире и даже есть в нас
самих.
Самыми яркими примерами выпуклых
дельтоидов в окружающем нас мире являются воздушный змей (Рис. 7.1), форма тела
рыбы (Рис 7.2), значок за высшее образование, который выдавали в СССР (Рис. 7.3),
а также они есть на логотипе популярного бренда одежды «STONE ISLAND»
(Рис. 7.4).
Самыми яркими же примерами
невыпуклого дельтоида являются дельтовидная мышца (Рис. 7.5) и дельтаплан (Рис.
7.6), также если посмотреть на форму крыльев самолёта, то можно тоже увидеть
невыпуклый дельтоид, но не так чётко как на дельтаплане.


Рис. 7.1
Рис. 7.2


Рис. 7.3 Рис.
7.4


Рис. 7.5
Рис. 7.6
Заключение
«Нет ничего нового под
солнцем, но есть кое-что старое, чего мы не знаем», – сказал Лоренс Питер.
Леонард Эйлер и Якоб Штейнер жил в 18 и 19 веках, но их исследования как
нельзя актуальны и сегодня. Новая для школьников геометрическая фигура
–дельтоид, интересная по своим свойствам,
Изучение ее повышает не только
интерес к изучению геометрии, но и сам процесс работы приносит удовлетворение.
В результате проделанной
исследовательской работы я могу сделать следующие выводы:
·
Дельтоид является
гармоническим четырехугольником.
·
Изучение
геометрической фигуры дельтоид, его свойств и признаков, облегчает решение
отдельных задач на ОГЕ и ЕГЕ
·
Дельтоида
нет в школьной программе Российской Федерации совершенно напрасно, так как
данная фигура очень часто встречается в окружающем нас мире и очень интересна
для изучения.
·
Все
поставленные в данной работе задачи решены, цель работы считаю достигнутой.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 февраля 2023 года; проверки требуют 12 правок.
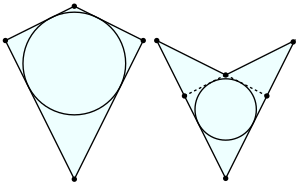
На чертеже слева дельтоид выпуклый, справа — невыпуклый.
Дельто́ид (от др.-греч. δελτοειδής — «дельтовидный», напоминающий заглавную букву дельта) — четырёхугольник, четыре стороны которого можно сгруппировать в две пары равных смежных сторон.
Свойства[править | править код]
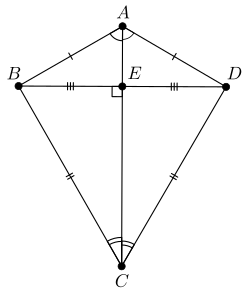
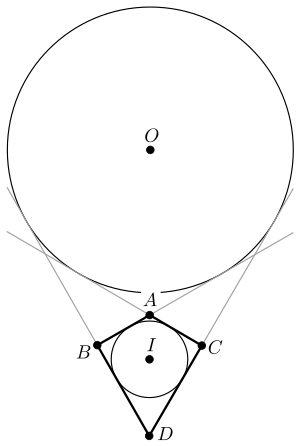
Вписанная и вневписанная окружности выпуклого дельтоида 
- Диагонали взаимно перпендикулярны.
- В любой выпуклый дельтоид можно вписать окружность
- Точка пересечения диагоналей делит одну из них пополам.
- Другая диагональ является биссектрисой углов.
- Одна диагональ делит дельтоид на два равных треугольника.
- Другая диагональ делит дельтоид на два равнобедренных треугольника, если он выпуклый, и достраивает его равнобедренным треугольником до равнобедренного треугольника, если он невыпуклый.
- Четырёхугольник, вершины которого совпадают с серединами сторон дельтоида, является прямоугольником, стороны которого параллельны диагоналям дельтоида. В частности, если этот прямоугольник — квадрат, то диагонали дельтоида равны, а отрезки, соединяющие середины противоположных сторон перпендикулярны между собой.
Дельтоид, который не является ромбом, обладает также следующими свойствами:
- Противоположные стороны имеют разные длины.
- Углы между сторонами неравной длины равны; другие два противоположных угла не равны.
- Если дельтоид выпуклый, то можно построить окружность, касающуюся продолжений всех четырёх сторон (см. рисунок).
- Если дельтоид невыпуклый, то можно построить окружность, касающуюся двух бо́льших сторон и продолжений двух меньших сторон, и окружность, касающуюся двух меньших сторон и продолжений двух бо́льших сторон.
Площадь дельтоида[править | править код]
- Здесь приведены формулы, свойственные именно дельтоиду. См. также формулы для площади произвольных четырёхугольников.
, где
и
— длины диагоналей.
, где
и
— длины неравных сторон, а
— угол между ними.
, где
и
— длины неравных сторон, а
— радиус вписанной окружности.
, где
и
— длины неравных сторон, а
и
— углы между равными сторонами соответственно.
Частные случаи[править | править код]
- Если угол между неравными сторонами дельтоида прямой, то вокруг него можно описать окружность (вписанный дельтоид).
- Если пара противоположных сторон дельтоида равна, то такой дельтоид является ромбом.
- Если пара противоположных сторон и обе диагонали дельтоида равны, то дельтоид является квадратом. Квадратом является и вписанный дельтоид с равными диагоналями.
Разное[править | править код]
- Дельтоидами являются грани дельтоидального икоситетраэдра, дельтоидального гексеконтаэдра и трапецоэдра.
|
Фестиваль исследовательских и творческих работ учащихся «Портфолио» Конкурс «Учебный проект» _________________________________________________________________________ |
|
Направление: Математика |
|
Тема: Выпуклый дельтоид на плоскости и в пространстве. |
Автор работы: ученик
СОШ ” Средняя общеобразовательная школа № 18″
г. Новокузнецк
Печёнкин А. Е.
Научный руководитель:
преподаватель математики,
Дамм Е.П.
|
2012 г. |
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
-
ВЫПУКЛЫЙ ДЕЛЬТОИД 4
-
Свойства выпуклого дельтоида 4
-
Признаки выпуклого дельтоида 5
-
Площади выпуклого дельтоида 7
-
-
ВЫПУКЛЫЙ ДЕЛЬТОИДНЫЙ МНОГОГРАННИК 10
-
Построение дельтоидного многогранника, его виды и свойства 10
-
Площади боковой и полной поверхности, объем выпуклого дельтоидного многогранника 11
-
ЗАКЛЮЧЕНИЕ 15
СПИСОК ЛИТЕРАТУРЫ 16
ВВЕДЕНИЕ
Актуальность. В настоящее время в школьном курсе геометрии, изучаются различные геометрические фигуры и тела, такие как круг, треугольник, четырехугольник, многоугольник, тетраэдр, параллелепипед, октаэдр и другие. Большая часть из них исследованы достаточно подробно, но существуют и такие, свойства и признаки которых до конца не изучены наукой – это, в частности, ромбоид, дельтоид, трапецоид, дельтоидный многогранник. В условиях увеличения интенсивности обучения геометрии, усложнения задач в итоговых аттестациях выпускных классов, наличия во второй части ЕГЭ задач, требующих углубленных знаний в области планиметрии и стереометрии, разработка научно обоснованного методического материала по таким фигурам позволит как существенно сократить время решения задач, так и будет способствовать более простым и изящным способам их решения. Кроме того, в прикладном плане научные знания о выпуклом дельтоиде и дельтоидном многограннике могут быть полезны при разработке и конструировании планеров летательных аппаратов, воздушных змеев, плавательных судов, а так же в области архитектуры и дизайна при создании рисунков декоративной мозаики. Поэтому, исследование свойств и признаков этих геометрических фигур на примере выпуклого дельтоида и выпуклого дельтоидного многогранника в настоящее время представляется весьма актуальной задачей.
Объектом исследования является выпуклый четырехугольник дельтоид, а также выпуклый дельтоидный многогранник.
Цель исследования – разработка методических подходов к изучению свойств и признаков выпуклого дельтоида, выпуклого дельтоидного многогранника, вывод формул площадей выпуклого дельтоида, объема, площади боковой и полной поверхности дельтоидного многогранника.
Реализация цели предполагала решение следующих задач:
-
систематизировать и обобщить понятия четырехугольников и дельтоида;
-
дать определение выпуклого дельтоида;
-
дать определение дельтоидного многогранника;
-
определить виды дельтоидных многогранников;
-
вывести и доказать новые свойства выпуклого дельтоида, дельтоидного мноогранника;
-
определить и обосновать признаки выпуклого дельтоида;
-
вывести формулы площади выпуклого дельтоида;
-
вывести формулы объема дельтоидного многогранника;
-
вывести площади боковой и полной поверхности дельтоидного многогранника.
Изучение выпуклого дельтоида, дельтоидного многогранника, их свойств и признаков ранее не было предметом самостоятельного научного анализа. Обоснование новых свойств, признаков выпуклого дельтоида и дельтоидного многогранника, а также вывод формул опирается на использование известных и доказанных теорем, используемых в геометрии, а также свойствами и признаками других геометрических фигур.
Наиболее существенные научные результаты, полученные лично автором, состоят в следующем:
-
Проведено специальное исследование и обобщение понятий четырехугольника, многоугольника и дельтоида.
-
Выведены и доказаны четыре новых свойства выпуклого дельтоида, определены и обоснованы его признаки, выведены и доказаны четыре новых формулы нахождения площади выпуклого дельтоида.
-
Определены виды выпуклого дельтоидного многогранника и дано определение каждому из видов.
ВЫПУКЛЫЙ ДЕЛЬТОИД
Дельтоид – четырёхугольник, обладающий двумя парами сторон одинаковой длины. Равными являются две пары смежных сторон.
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Таким образом, выпуклый дельтоид – это четырёхугольник, у которого две пары смежных сторон равны и который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
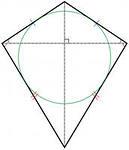
Из определения дельтоида следует, что и ромб, и квадрат также являются дельтоидами. Ромб – это параллелограмм, у которого все стороны равны
Квадрат – это ромб с прямыми углами. Значит, ромб и квадрат имеют две пары равных смежных сторон.
Свойства выпуклого дельтоида.
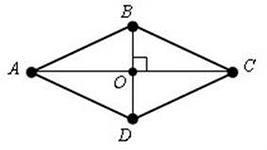
Выясним, какими свойствами обладает выпуклый дельтоид  , у которого
, у которого 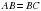 ,
, 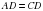 .
.

1) Проведём диагональ  и рассмотрим треугольники
и рассмотрим треугольники 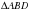 и
и 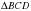 .
.
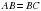 – по условию;
– по условию;
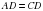 – по условию;
– по условию;
 – общая сторона.
– общая сторона.
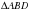 =
=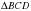 по трём сторонам.
по трём сторонам.
Из равенства треугольников следует, что 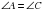 ,
, 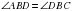 ,
, 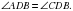 То есть в выпуклом дельтоиде углы между сторонами неравной длины равны и диагональ, соединяющая вершины неравных углов является биссектрисой (
То есть в выпуклом дельтоиде углы между сторонами неравной длины равны и диагональ, соединяющая вершины неравных углов является биссектрисой (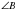 и
и 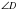 не могут быть равными, так как
не могут быть равными, так как 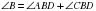 ,
,  , а
, а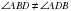 , так как это не углы при основании равнобедренного треугольника, аналогично
, так как это не углы при основании равнобедренного треугольника, аналогично 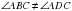 ).
).
2) Проведём диагональ 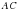 . Рассмотрим треугольники
. Рассмотрим треугольники 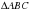 и
и 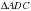 . Они равнобедренные по определению (треугольник называется равнобедренным, если у него две стороны равны0).
. Они равнобедренные по определению (треугольник называется равнобедренным, если у него две стороны равны0).
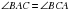 – так как это углы при основании равнобедренного треугольника.
– так как это углы при основании равнобедренного треугольника.
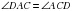 – так как это углы при основании равнобедренного треугольника.
– так как это углы при основании равнобедренного треугольника.
Так как 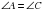 (ранее доказанное, смотрите п.1),
(ранее доказанное, смотрите п.1), 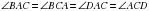 , следовательно
, следовательно 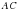 – биссектриса (по определению). Точка
– биссектриса (по определению). Точка 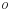 – точка пересечения диагоналей.
– точка пересечения диагоналей. 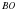 – отрезок биссектрисы
– отрезок биссектрисы 
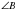 (смотрите выше), проведённый к основанию равнобедренного треугольника
(смотрите выше), проведённый к основанию равнобедренного треугольника 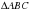 , следовательно,
, следовательно, 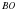 – высота и медиана этого треугольника (значит,
– высота и медиана этого треугольника (значит,  ).
). 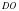 – отрезок биссектрисы
– отрезок биссектрисы 
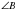 (смотрите выше), проведённый к основанию равнобедренного треугольника
(смотрите выше), проведённый к основанию равнобедренного треугольника 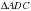 , следовательно,
, следовательно, 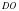 – высота и медиана этого треугольника (значит,
– высота и медиана этого треугольника (значит,  ). Таким образом, диагонали выпуклого дельтоида взаимно перпендикулярны и при пересечении диагоналей, диагональ, соединяющая вершины равных углов, делится пополам.
). Таким образом, диагонали выпуклого дельтоида взаимно перпендикулярны и при пересечении диагоналей, диагональ, соединяющая вершины равных углов, делится пополам.
3) Выясним, можно ли вписать в любой выпуклый дельтоид окружность. Известно, что окружность можно вписать только в такой выпуклый четырёхугольник, у которого суммы противолежащих сторон равны. В выпуклом четырёхугольнике  , в котором
, в котором 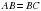 ,
, 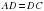 ,
, 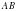 и
и  – противолежащие стороны,
– противолежащие стороны, и
– противолежащие стороны.
Вывод: Следовательно, в любой выпуклый дельтоид можно вписать окружность.
Таким образом, в ходе исследования выведены следующие свойства:
-
В выпуклом дельтоиде углы между сторонами неравной длины равны.
-
Диагонали являются биссектрисами углов дельтоида.
-
Диагонали выпуклого дельтоида взаимно перпендикулярны и при пересечении диагоналей, диагональ, соединяющая вершины равных углов, делится пополам.
-
В любой выпуклый дельтоид можно вписать окружность.
Признаки выпуклого дельтоида.
Выясним, какими признаками обладают выпуклые дельтоиды.
1) Выясним, что можно сказать о выпуклом четырёхугольнике, у которого диагонали пересекаются под прямым углом, и одна из диагоналей при этом делится пополам
Дано:
 – выпуклый четырёхугольник;
– выпуклый четырёхугольник; 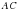 и
и  – диагонали данного четырехугольника,
– диагонали данного четырехугольника, ,
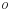 – точка пересечения диагоналей,
– точка пересечения диагоналей, .
Исследуем этот четырёхугольник.
Рассмотрим 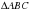 .
.
Диагональ по условию. Согласно определения, перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
Отсюда следует, что 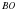 – высота.
– высота.
– по условию. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Следовательно,
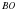 – медиана. Если в треугольнике высота одновременно является и медианой, то данный треугольник равнобедренный, то
– медиана. Если в треугольнике высота одновременно является и медианой, то данный треугольник равнобедренный, то 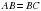 . Аналогично можно доказать, что треугольник
. Аналогично можно доказать, что треугольник равнобедренный, а значит,
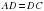 .
.
Вывод:  – дельтоид по определению.
– дельтоид по определению.
Итак, определен и доказан первый признак дельтоида: если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, и одна из диагоналей при этом делится пополам, то данный четырёхугольник – дельтоид.
2) Исследуем выпуклый четырёхугольник  , у которого диагонали пересекаются под прямым углом, и одна из диагоналей является биссектрисой углов этого четырёхугольника. Напомним, что биссектриса угла – луч с началом в вершине угла, делящий угол на две равные части.
, у которого диагонали пересекаются под прямым углом, и одна из диагоналей является биссектрисой углов этого четырёхугольника. Напомним, что биссектриса угла – луч с началом в вершине угла, делящий угол на две равные части.
Дано:
 – выпуклый четырёхугольник;
– выпуклый четырёхугольник; 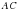 и
и  – диагонали данного четырехугольника,
– диагонали данного четырехугольника, ,
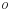 – точка пересечения диагоналей,
– точка пересечения диагоналей,  – биссектриса.
– биссектриса.
Исследуем данный четырехугольник.
Рассмотрим 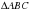 .
.
Так как по условию, то
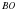 – высота.
– высота.
Так как  – биссектриса (по условию) и
– биссектриса (по условию) и 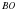 – высота, в треугольнике высота одновременно является и биссектрисой, то данный треугольник равнобедренный0, значит
– высота, в треугольнике высота одновременно является и биссектрисой, то данный треугольник равнобедренный0, значит 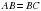 . Аналогично можно доказать, что
. Аналогично можно доказать, что – равнобедренный, а это значит, что
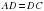 .
.
Вывод:  – дельтоид по определению.
– дельтоид по определению.
Итак, определен и доказан второй признак дельтоида: если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, и одна из диагоналей является биссектрисой углов этого четырёхугольника, то данный четырёхугольник – дельтоид.
3) Исследуем выпуклый четырёхугольник  , у которого одна из диагоналей – биссектриса двух равных углов этого четырёхугольника.
, у которого одна из диагоналей – биссектриса двух равных углов этого четырёхугольника.
Дано:
 – выпуклый четырёхугольник;
– выпуклый четырёхугольник; 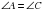 ,
, 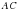 – биссектриса.
– биссектриса.
Исследуем данный четырехугольник.
Рассмотрим 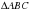 .
.
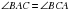 , так как это половинки равных углов
, так как это половинки равных углов и
(
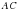 – биссектриса по условию). Если в треугольнике два угла равны, то он равнобедренный, значит
– биссектриса по условию). Если в треугольнике два угла равны, то он равнобедренный, значит 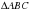 – равнобедренный, поэтому
– равнобедренный, поэтому 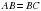 . Аналогично доказывается, что
. Аналогично доказывается, что – равнобедренный, отсюда следует, что
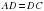 .
.
Вывод:  – дельтоид по определению.
– дельтоид по определению.
Итак, определен и доказан третий признак дельтоида: если в выпуклом четырёхугольнике одна из диагоналей – биссектриса двух равных углов этого четырёхугольника, то данный четырёхугольник – дельтоид.
4) Исследуем выпуклый четырёхугольник  , у которого диагонали пересекаются под прямым углом, а две смежных стороны равны.
, у которого диагонали пересекаются под прямым углом, а две смежных стороны равны.
Дано:
 – выпуклый четырёхугольник;
– выпуклый четырёхугольник; 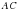 и
и  – диагонали данного четырехугольника,
– диагонали данного четырехугольника, ,
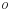 – точка пересечения диагоналей,
– точка пересечения диагоналей, 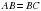 .
.
Исследуем данный четырехугольник.
Рассмотрим 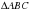 .
.
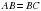 по условию, следовательно
по условию, следовательно 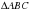 – равнобедренный по определению. Так как диагональ
– равнобедренный по определению. Так как диагональ по условию, то
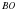 – высота, проведённая к основанию равнобедренного треугольника, следовательно
– высота, проведённая к основанию равнобедренного треугольника, следовательно 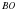 – медиана (по свойству высоты в равнобедренном треугольнике). Отсюда следует, что
– медиана (по свойству высоты в равнобедренном треугольнике). Отсюда следует, что .
Рассмотрим 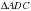 .
.
Так как 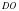 – высота, и
– высота, и , следовательно,
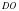 – медиана. Если высота в треугольнике является медианой, то он равнобедренный, значит
– медиана. Если высота в треугольнике является медианой, то он равнобедренный, значит 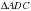 – равнобедренный,
– равнобедренный, 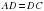 .
.
Вывод:  – дельтоид по определению.
– дельтоид по определению.
Итак, определен и доказан четвёртый признак дельтоида: если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, а две смежных стороны равны, то данный четырёхугольник – дельтоид.
Таким образом, в работе были определены и доказаны четыре признака дельтоида:
-
Если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, и одна из диагоналей при этом делится пополам, то данный четырёхугольник – дельтоид.
-
Если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, и одна из диагоналей является биссектрисой углов этого четырёхугольника, то данный четырёхугольник – дельтоид.
-
Если в выпуклом четырёхугольнике одна из диагоналей – биссектриса двух равных углов этого четырёхугольника, то данный четырёхугольник – дельтоид.
-
Если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, а две смежных стороны равны, то данный четырёхугольник – дельтоид.
Рассмотрим применение свойств и признаков дельтоида на практике (при решении задач).
ПРИМЕР. Задача: На стороне 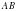 и
и прямоугольника
 взяты т.
взяты т. и т.
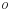 соответственно так, что
соответственно так, что , а на стороне
взята т.
так, что
. Найти
.
Дано:
 – прямоугольник
– прямоугольник
Найти:
Решение:
-
, так как это угол прямоугольника
-
Рассмотрим четырёхугольник
.
по условию;
по условию
Вывод: – дельтоид по определению.
-
– диагональ дельтоида, а так как диагонали дельтоида являются биссектрисами углов дельтоида, то
.
Значит
Ответ: .
Площади выпуклого дельтоида.
Площадь дельтоида также можно найти по формуле , где
и
длины неравных сторон, а α угол между ними. Докажем это.
Доказательство.
В выпуклом дельтоиде проведём диагональ
, которая разделит его на два равных треугольника
и
(
, по условию;
, по условию;
– общая), то есть площади этих треугольников равны. Площадь дельтоида
равна сумме площадей треугольников
и
или 2 × S∆АВС. Площадь
. Таким образом,
. А площадь любого дельтоида можно найти по формуле
, где
и
– неравные стороны дельтоида,
– угол между сторонами
и
.
Выведем другие формулы нахождения площади основания дельтоидного многогранника, то есть площади выпуклого дельтоида.
Для этого рассмотрим выпуклый дельтоид , у которого
,
(рис.9).
Проведём диагональ , которая разделит дельтоид на два треугольника
и
. Площадь дельтоида будет равна сумме площадей этих треугольников.
Рассмотрим треугольники и
. Они равнобедренные, так как
,
по условию (равнобедренным называется треугольник, у которого две стороны равны).
Известно, что площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Таким образом площади и
равны
и
соответственно. А так как
,
по условию, то площади
и
равны
и
соответственно. Тогда площадь дельтоида
будет равна .
Найдем площадь выпуклого дельтоида используя формулу Герона.
Площади треугольников 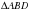 и
и также можно найти по формуле Герона:
, где
,
,
,
– стороны треугольника.
Пусть в и
,
,
.
Тогда
;
Аналогично ,
. Таким образом, площадь дельтоида равна .
Таким образом, в ходе исследования выведены и доказаны формулы нахождения площади выпуклого дельтоида:
-
Площадь дельтоида равна половине произведения его диагоналей.
-
, где
и
– длины неравных сторон, а α угол между ними.
-
, где
– диагональ основания дельтоидного многогранника, соединяющая общие вершины неравных сторон основания,
и
– неравные стороны основания.
-
, где
и
– неравные стороны выпуклого дельтоида; α и β – углы дельтоида, лежащие между его равными сторонами.
Площади боковой и полной поверхности,
объем выпуклого дельтоидного многогранника.
Выясним, чему равен объём дельтоидного многогранника. Напомним, что объём — вместимость геометрического тела, т. е. части пространства, ограниченной одной или несколькими замкнутыми поверхностями.
Выведем формулу для нахождения объёма дельтоидного многогранника.
Основанием дельтоидного многогранника является дельтоид (смотрите выше). Площадь дельтоида равна половине произведения его диагоналей. Таким образом, объём дельтоидного многогранника равен половине произведения диагоналей его основания на высоту этого дельтоидного многогранника: , где
и
– диагонали основания дельтоидного многогранника,
– его высота. Докажем это.
Рассмотрим дельтоидный многогранник .
Проведём диагональ , условно разделив данный многогранник на два многогранника:
и
). Достроим многогранник
до параллелепипеда
(призмы, основанием которой служит параллелограмм).
Для этого проведём параллельный отрезку отрезок
, параллельный отрезку
отрезок
, отрезки
и
параллельные
и
соответственно. Соединим точки
и
(рис.13) (см. Приложение). Получившийся параллелепипед будет состоять из двух равных многогранников
и
. Докажем это. Согласно определению, у параллелепипеда основаниями являются параллелограммы. Если мы проведём диагонали
и
оснований
и
соответственно, то разделим каждое основание на два равных треугольника
и
(
, так как противоположные углы параллелограмма равны,
и
, так как противоположные стороны параллелограмма равны =
по двум сторонам и углу между ними). Аналогично равны
. Согласно свойству параллелепипеда, его противолежащие грани параллельны и равны. Следовательно,
,
. Известно, что две фигуры называются конгруэнтными, или равными, если существует изометрия плоскости, которая переводит одну в другую. Другими словами, если основания и боковые грани одного многогранника равны основаниям и граням другого, то такие многогранники равны. Вывод: многогранники
и
равны, то есть параллелепипед
состоит из двух равных многогранников, один из которых является частью дельтоидного многогранника
. Известно, что объём параллелепипеда равен произведению площади основания на высоту . А так как многогранник
– это половина параллелепипеда
(смотрите выше), то соответственно и объём многогранника
равен половине объёма параллелепипеда, то есть половине произведения площади основания параллелепипеда на высоту. А так как основание параллелепипеда – это параллелограмм, то половина площади параллелограмма
– это площадь
(площадь треугольника равна половине произведения основания на проведённую к нему высоту). Таким образом, объём многогранника
равен половине произведения основания на высоту. Аналогично можно найти объём многогранника
(второй половины дельтоидного многогранника
). Известно, что если геометрическое тело составлено из геометрических тел, не имеющих общих внутренних точек, то объем данного тела равен сумме объемов тел его составляющих. Таким образом, мы можем говорить о том, что объём любого дельтоидного многогранника равен сумме объёмов частей, на которые делится этот многогранник его диагональю (отрезком, соединяющим две вершины дельтоидного многогранника, не принадлежащим одной грани). Найдя, объём каждой такой части и сложив полученные значения, мы найдём объём дельтоидного многогранника.
Дано: дельтоидный многогранник .
Найти: -?
Решение:
Проведём диагональ , которая разделит данный многогранник
на два многогранника:
и
(рис.14) (см. Приложение).
Вывод: , где и
– диагонали основания дельтоидного многогранника
.
Так как, площадь дельтоида также можно найти по формуле , где
и
длины неравных сторон, а α угол между ними, то
.
Таким образом, объём дельтоидного многогранника равен произведению двух неравных сторон его основания, умноженному на синус угла между ними, на высоту дельтоидного многогранника: , где – высота дельтоидного многогранника.
и
длины неравных сторон, α угол между ними,
Так как, основанием дельтоидного многогранника является выпуклый дельтоид и его площадь равна (доказательство выше), то объём дельтоидного многогранника равен
, где
и
– неравные стороны основания; α и β – основания, лежащие между его равными сторонами;
– высота дельтоидного многогранника.
Так как, площадь основания дельтоидного многогранника равна , то объем этого многогранника равен , где – диагональ основания дельтоидного многогранника, соединяющая общие вершины неравных сторон основания,
и
– неравные стороны основания,
– высота дельтоидного многогранника.
Для нахождения площади полной поверхности (объединения оснований и боковой поверхности) дельтоидного многогранника достаточно сложить значения площадей всех его граней. Рассмотрим грани дельтоидного многогранника.
Основания являются равными дельтоидами (смотрите выше).
Боковые грани, рёбра которых являются равными сторонами основания дельтоидного многогранника, равны. Докажем это на примере дельтоидного многогранника (рис.15).
Рассмотрим боковые грани и
.
-
и
– параллелограммы, (смотрите выше);
-
, смотрите выше;
-
, как противолежащие стороны параллелограмма (противоположные стороны параллелограмма равны);
-
, как противолежащие стороны параллелограмма.
Вывод: .
Аналогично доказывается равенство боковых граней .
Таким образом, для нахождения площади полной поверхности дельтоидного многогранника достаточно знать площади его боковых граней, рёбра которых являются неравными сторонами этого дельтоидного многогранника, и площадь основания. Сложив значения площадей каждой такой боковой грани и площади основания и умножив сумму этих площадей на два, мы получим значение площади полной поверхности дельтоидного многогранника. Для нахождения площади боковой поверхности дельтоидного многогранника нужно сложить значения площадей боковых граней, рёбра которых являются неравными сторонами основания, и умножить полученную сумму площадей на два.
Проведём диагональ дельтоидного многогранника из вершины его основания, являющийся общей для равных сторон этого основания. На рисунке это диагональ . Докажем, что эта диагональ делит дельтоидный многогранник
, у которого
и
, на два равных многогранника
и
. Рассмотрим
и
.
-
( смотрите выше);
-
(смотрите выше);
-
, по условию;
-
, по условию;
-
, так как это соответственные диагонали оснований дельтоидного многогранника.
Вывод: по трём сторонам;
по трём сторонам.
Вывод: .
Итак мы доказали, что диагональ дельтоидного многогранника, проведённая из вершины основания, являющейся общей для его равных сторон, делит дельтоидный многогранник на два равных многогранника.
Рассмотрим прямой дельтоидный многогранник.
В прямом дельтоидном многограннике все боковые рёбра перпендикулярны основанию (смотрите выше). А так как высота – отрезок, соединяющий основания многогранника и перпендикулярный им, то боковые рёбра прямого дельтоидного многогранника являются также его высотой. Объём дельтоидного многогранника равен произведению площади его основания на высоту этого дельтоидного многогранника (смотрите выше). Значит, объём прямого дельтоидного многогранника равен произведению площади его основания на боковую грань.
Известно, что площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы. А так как дельтоидный многогранник – призма по определению (смотрите выше), то площадь боковой поверхности прямого дельтоидного многогранника равна произведению периметра его основания на высоту дельтоидного многогранника.
Таким образом, в ходе исследования выпуклого дельтоидного многогранника дано определение дельтоидного многогранника, установлены правила его построения, определены его виды, выведены следующие свойства:
-
Основаниями дельтоидного образования являются выпуклые дельтоиды.
-
Боковые грани являются параллелограммами.
-
Объём дельтоидного многогранника равен половине произведения диагоналей его основания на высоту этого дельтоидного многогранника:
, где
и
– диагонали основания дельтоидного многогранника,
– его высота.
Объём дельтоидного многогранника равен произведению двух неравных сторон его основания, умноженному на синус угла между ними, на высоту дельтоидного многогранника: , где
и
длины неравных сторон, α угол между ними,
– высота дельтоидного многогранника.
, где и
– неравные стороны выпуклого дельтоида; α и β – углы дельтоида, лежащие между его равными сторонами;
– высота дельтоидного многогранника.
, где – диагональ основания дельтоидного многогранника, соединяющая общие вершины неравных сторон основания, – неравные стороны основания,
высота дельтоидного многогранника.
-
Для нахождения площади полной поверхности дельтоидного многогранника нужно сложить площади его боковых граней, рёбра которых являются неравными сторонами этого дельтоидного многогранника, с площадью основания, и умножить полученную сумму на два.
-
Для нахождения площади боковой поверхности дельтоидного многогранника нужно сложить значения площадей боковых граней, рёбра которых являются неравными сторонами основания, и умножить полученную сумму площадей на два.
-
Диагональ дельтоидного многогранника, проведённая из вершины основания, являющейся общей для его равных сторон, делит дельтоидный многогранник на два равных многогранника.
-
Объём прямого дельтоидного многогранника равен произведению площади его основания на боковую грань.
-
Площадь боковой поверхности прямого дельтоидного многогранника равна произведению периметра его основания на высоту.
Таким образом, цель исследовательской работы выполнена.
ЗАКЛЮЧЕНИЕ
Таким образом, в процессе исследований были даны определения выпуклого дельтоида и выпуклого дельтоидного многогранника, изложены их свойства, доказаны признаки, выведены и доказаны формулы нахождения площади выпуклого дельтоида, объема выпуклого дельтоидного многогранника, площади полной и боковой поверхности.
В качестве направлений для дальнейших исследований предполагается рассмотреть свойства аналогичных фигур в планиметрии и стереометрии.
СПИСОК ЛИТЕРАТУРЫ
-
http://gazpromschool.by.ru/projects/geometry/tr/tr312_1a.htm
-
http://geometricheskie.narod.ru/3D/Vparallelepiped.html
-
http://dic.academic.ru/dic.nsf/business/8852
-
Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. Геометрия 7-9 классы.б Учебник. 15-е изд. М.:”Просвещение“, 2005.
-
Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев «Геометрия 10-11 класс»; издательство «Просвещение», 1996.
-
О.В.Георгиевский. Начертательная геометрия ( сборник задач с решением типовых примеров). АСТ; Астрель, 2002.
-
Я.И. Пелерман. Занимательная алгебра, геометрия. Изд-во: Книга, 2005.
0 gazpromschool.by.ru/projects/geometry/tr/tr312_1a.htm
0 gazpromschool.by.ru/projects/geometry/tr/tr312_1a.htm
Дельтоид
Материал из Большого Справочника

На чертеже слева дельтоид выпуклый, справа — невыпуклый.
Дельто́ид (от др.-греч. δελτοειδής — «дельтовидный», напоминающий заглавную букву дельта) — четырёхугольник, в котором есть две пары смежных равных сторон.
Свойства


Вписанная и вневписанная окружности выпуклого дельтоида 
- Углы между сторонами неравной длины равны.
- Диагонали взаимно перпендикулярны.
- В любой выпуклый дельтоид можно вписать окружность; кроме того, если дельтоид не является ромбом, то существует ещё одна окружность, касающаяся продолжений всех четырёх сторон (см. рисунок).
- Для любого невыпуклого дельтоида можно построить окружность, касающуюся двух бо́льших сторон и продолжений двух меньших сторон, и окружность, касающуюся двух меньших сторон и продолжений двух бо́льших сторон.
- Точка пересечения диагоналей делит одну из них пополам.
- Другая диагональ является биссектрисой углов.
- Одна диагональ делит дельтоид на два равных треугольника.
- Другая диагональ делит дельтоид на два равнобедренных треугольника, если он выпуклый, и достраивает его равнобедренным треугольником до равнобедренного треугольника, если он невыпуклый.
Площадь дельтоида
- Здесь приведены формулы, свойственные именно дельтоиду. См. также формулы для площади произвольных четырёхугольников.
, где
и
— длины диагоналей.
, где
и
— длины неравных сторон, а
— угол между ними.
Частные случаи
- Если угол между неравными сторонами дельтоида прямой, то вокруг него можно описать окружность (вписанный дельтоид).
- Если пара противоположных сторон дельтоида равна, то такой дельтоид является ромбом.
- Если пара противоположных сторон и обе диагонали дельтоида равны, то дельтоид является квадратом. Квадратом является и вписанный дельтоид с равными диагоналями.
Разное
- Дельтоидами являются грани дельтоидального икоситетраэдра, дельтоидального гексеконтаэдра и трапецоэдра.


