Куб является базовым геометрическим телом, когда речь заходит об объеме и объемных телах. Недаром третья степень, которая получается умножением трех одинаковых чисел друг на друга (как при нахождении объема куба – трех его измерений одинаковых измерений) названа в его честь.
Основным и единственным параметром куба является его ребро a,так как все ребра у куба конгруэнтны, и представляют собой одновременно и длину, и ширину, и высоту. Соответственно, всего одно значение определяет все возможные характеристики куба, связанные с его измерениями.
Помимо ребер, вершины куба можно соединить диагоналями. Диагонали могут проходить через грани куба, тогда они будут просто диагональю основания или диагональю квадрата в плоскости, либо диагонали могут быть проведены внутри самого куба, соединяя противоположные основания в крайних точках (вершинах).
Чтобы найти диагональ куба через его ребро, необходимо сначала провести дополнительное построение в виде диагонали одного из соединяемых оснований, тогда диагональ куба станет гипотенузой новоиспеченного прямоугольного треугольника, катетами которого являются ребро куба и диагональ основания. Если ребро куба задано условиями задачи, то диагональ квадрата в основании придется сначала вычислить по формуле:
d=a√2
Тогда диагональ куба можно будет выразить через теорему Пифагора, и она примет следующий вид:
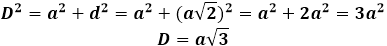
Диагональ куба
Диагональ
Правильный многогранник, все грани которого являются квадратами, называется кубом. Все ребра у куба равны, а углы прямые. Диагональ стороны куба d или его боковой грани, представляющей собой квадрат, определяем по формуле диагонали квадрата, как произведение стороны квадрата (ребра куба) (а) на корень квадратный из двух: d=a√2
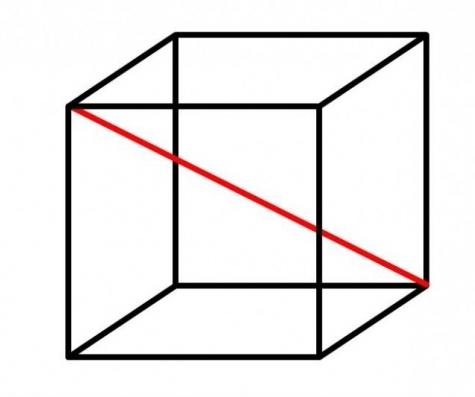
Диагональю куба является отрезок, который соединяет две вершины, расположенные на противоположных сторонах куба. Вершины расположены симметрично по отношению к центру куба. Для определения диагонали куба вписываем в куб прямоугольный треугольник, соединив диагональ куба, диагональ основания и боковое ребро, исходящее из вершины основания. Воспользовавшись теоремой Пифагора, вычисляем диагональ куба, которая равна произведению ребра куба (а) на корень квадратный из трех.
![]()
Калькулятор для расчета диагонали куба
Что такое куб, и какие диагонали он имеет
Куб (правильный многогранник или гексаэдр) представляет собой объемную фигуру, каждая грань – это квадрат, у которого, как нам известно, все стороны равны. Диагональю куба является отрезок, который проходит через центр фигуры и соединяет симметричные вершины. В правильном гексаэдре имеется 4 диагонали, и все они будут равны. Очень важно не путать диагональ самой фигуры с диагональю ее грани или квадрата, который лежит на его основании. Диагональ грани куба проходит через центр грани и соединяет противоположные вершины квадрата.
Формула, по которой можно найти диагональ куба
Диагональ правильного многогранника можно найти по очень простой формуле, которую необходимо запомнить. D=a√3, где D обозначаем диагональ куба, а – это ребро. Приведем пример задачи, где необходимо найти диагональ, если известно, что длина его ребра равна 2 см. Здесь все просто D = 2√3, даже считать ничего не надо. Во втором примере, пусть ребро куба будет равно √3 см, то тогда получаем D = √3√3=√9=3. Ответ: D равен 3 см.
Формула, по которой можно найти диагональ грани куба
Диаго
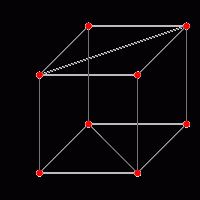
наль грани можно также найти по формуле. Диагоналей, которые лежат на гранях, всего 12 штук, и они все равны между собой. Теперь запоминаем d=a√2, где d – это диагональ квадрата, а – это также ребро куба или сторона квадрата. Понять откуда взялась эта формула, очень просто. Ведь две стороны квадрата и диагональ образуют прямоугольный треугольник. В этом трио диагональ играет роль гипотенузы, а стороны квадрата – это катеты, которые имеют одинаковую длину. Вспомним теорему Пифагора, и все тут же встанет на свои места. Теперь задача: ребро гексаэдра равняется √8 см, необходимо найти диагональ его грани. Вставляем в формулу, и у нас получается d=√8 √2=√16=4. Ответ: диагональ грани куба равняется 4 см.
Если известна диагональ грани куба
По условию задачи, нам дана только диагональ грани правильного многогранника, которая равна, предположим, √2 см, а нам необходимо найти диагональ куба. Формула решения этой задачи немного сложнее предыдущей. Если нам известно d, то мы можем найти ребро куба, исходя из нашей второй формулы d=a√2. Получаем а= d/√2= √2/√2=1см (это наше ребро). А если известна эта величина, то найти диагональ куба не составит труда: D = 1√3= √3. Вот так мы решили нашу задачку.
Если известна площадь поверхности

Следующий алгоритм решения строится на нахождении диагонали по площади поверхности куба. Предположим, что она равна 72 см2. Для начала найдем площадь одной грани, а всего их 6. Значит, 72 необходимо поделить на 6, получаем 12 см2. Это площадь одной грани. Чтобы найти ребро правильного многогранника, необходимо вспомнить формулу S=a2, значит a=√S. Подставляем и получаем a=√12 (ребро куба). А если мы знаем это значение, то и диагональ найти не сложно D= a√3= √12 √3 = √36 = 6. Ответ: диагональ куба равна 6 см2.
Если известна длина ребер куба
Бывают такие случаи, когда в задаче дана только длина всех ребер куба. Тогда необходимо это значение разделить на 12. Именно столько сторон в правильном многограннике. Например, если сумма всех ребер равна 40, то одна сторона будет равна 40/12=3,333. Вставляем в нашу первую формулу и получаем ответ!
Куб или как его еще называют гексаэдр – это правильный многогранник, каждая из граней которого имеет форму квадрата. Куб – это частный случай призмы и параллелепипеда.
Разные дисциплины используют значение этого термина по отношению к различным свойствам геометрического прототипа. Например, в аналитике применяют аналитические многомерные кубы, которые позволяют наглядно сопоставить данные из разных таблиц.
Свойства куба
- В куб можно вписать тетраэдр двумя вариантами, причем вершины тетраэдра, а их четыре, будут совпадать с четырьмя вершинами куба. Все шесть ребер тетраэдра будут располагаться на всех шести гранях куба и будут равны диагонали грани квадрата.
- Четыре сечения куба это правильные шестиугольники, они проходят по центру куба перпендикулярно четырем диагоналям.
- В куб вписывается октаэдр, причем все шесть вершин октаэдра совместятся с центрами шести граней куба.
- Куб вписывается в октаэдр, причем все восемь вершин куба расположатся в центрах восьми граней октаэдра.
- В куб можно вписать икосаэдр, так, что шесть взаимно параллельных ребер икосаэдра расположатся на шести гранях куба, остальные двадцать четыре ребра внутри куба, все 12 вершин икосаэдра лягут по шести граням куба.
Формулы для куба
- Поверхность куба: A = 6*a2
- Объем куба: V = a3
- Диагональ куба: d = a*√3
Инструкция
Если длина ребра куба
(a) известна из условий задачи, формулу расчета длины диагонали грани (l) можно вывести из теоремы Пифагора. В кубе любые два смежных ребра образуют прямой угол, поэтому треугольник, составленный из них грани, является прямоугольным. Ребра в этом случае – катеты, а рассчитать вам нужно длину гипотенузы. Согласно упомянутой выше теореме она равна квадратному корню из суммы квадратов длин , а так как в данном случае они одинаковые размеры, просто умножьте длину ребра на квадратный корень из двойки: l = √(a²+a²) = √(2*a²) = a*√2.
Люди с каждым днем люди развиваются, но какие бы достижения ни были совершены, человечество не в бороться с различными климатическими капризами или же с природными катастрофами. Природа всегда готовит какие-то сюрпризы. Вот снег в Африке, последствием чего стало огромное количество жертв. Люди просто замерзали, ведь их оказался совершенно не приспособлен к таким условиям.
Именно поэтому человечество оказывается просто не в силах бороться с силами природы, а ее причуды уносят все новые и новые жизни.
Из всего этого следует вывод: конечно же, человечество находится на грани своего развития, но и благодаря тому, что он , увеличивается и риск оказаться на грани вымирания. Поэтому не следует думать, что с проблемами нужно бороться по мере их поступления, лучше думать заранее, так, чтобы не допустить в будущем глобальной катастрофы.
Видео по теме
Или гексаэдр) представляет собой объемную фигуру, каждая грань – это квадрат, у которого, как нам известно, все стороны равны. Диагональю куба является отрезок, который проходит через центр фигуры и соединяет симметричные вершины. В правильном гексаэдре имеется 4 диагонали, и все они будут равны. Очень важно не путать диагональ самой фигуры с диагональю ее грани или квадрата, который лежит на его основании. Диагональ грани куба проходит через центр грани и соединяет противоположные вершины квадрата.
Формула, по которой можно найти диагональ куба
Диагональ правильного многогранника можно найти по очень простой формуле, которую необходимо запомнить. D=a√3, где D обозначаем диагональ куба, а – это ребро. Приведем пример задачи, где необходимо найти диагональ, если известно, что длина его ребра равна 2 см. Здесь все просто D = 2√3, даже считать ничего не надо. Во втором примере, пусть ребро куба будет равно √3 см, то тогда получаем D = √3√3=√9=3. Ответ: D равен 3 см.
Формула, по которой можно найти диагональ грани куба

наль грани можно также найти по формуле. Диагоналей, которые лежат на гранях, всего 12 штук, и они все равны между собой. Теперь запоминаем d=a√2, где d – это диагональ квадрата, а – это также ребро куба или сторона квадрата. Понять откуда взялась эта формула, очень просто. Ведь две стороны квадрата и диагональ образуют В этом трио диагональ играет роль гипотенузы, а стороны квадрата – это катеты, которые имеют одинаковую длину. Вспомним теорему Пифагора, и все тут же встанет на свои места. Теперь задача: ребро гексаэдра равняется √8 см, необходимо найти диагональ его грани. Вставляем в формулу, и у нас получается d=√8 √2=√16=4. Ответ: диагональ грани куба равняется 4 см.
Если известна диагональ грани куба
По условию задачи, нам дана только диагональ грани правильного многогранника, которая равна, предположим, √2 см, а нам необходимо найти диагональ куба. Формула решения этой задачи немного сложнее предыдущей. Если нам известно d, то мы можем найти ребро куба, исходя из нашей второй формулы d=a√2. Получаем а= d/√2= √2/√2=1см (это наше ребро). А если известна эта величина, то найти диагональ куба не составит труда: D = 1√3= √3. Вот так мы решили нашу задачку.
Если известна площадь поверхности

Следующий алгоритм решения строится на нахождении диагонали по Предположим, что она равна 72 см 2 . Для начала найдем площадь одной грани, а всего их 6. Значит, 72 необходимо поделить на 6, получаем 12 см 2 . Это площадь одной грани. Чтобы найти ребро правильного многогранника, необходимо вспомнить формулу S=a 2 , значит a=√S. Подставляем и получаем a=√12 (ребро куба). А если мы знаем это значение, то и диагональ найти не сложно D= a√3= √12 √3 = √36 = 6. Ответ: диагональ куба равна 6 см 2 .
Если известна длина ребер куба
Бывают такие случаи, когда в задаче дана только длина всех ребер куба. Тогда необходимо это значение разделить на 12. Именно столько сторон в правильном многограннике. Например, если сумма всех ребер равна 40, то одна сторона будет равна 40/12=3,333. Вставляем в нашу первую формулу и получаем ответ!
Если шесть граней квадратной формы ограничивают некоторый объем пространства, то геометрическую форму этого пространства можно назвать кубической или гексаэдрической. Все двенадцать ребер такой пространственной фигуры имеют одинаковую длину, что значительно упрощает вычисления параметров многогранника. Длина диагонали куба
– не исключение, ее можно найти многими способами.
Инструкция
- Если длина ребра куба
(a) известна из условий задачи, формулу расчета длины диагонали грани (l) можно вывести из теоремы Пифагора. В кубе любые два смежных ребра образуют прямой угол, поэтому треугольник, составленный из них и диагонали грани, является прямоугольным. Ребра в этом случае – катеты, а рассчитать вам нужно длину гипотенузы. Согласно упомянутой выше теореме она равна квадратному корню из суммы квадратов длин катетов, а так как в данном случае они имеют одинаковые размеры, просто умножьте длину ребра на квадратный корень из двойки: l = √(a²+a²) = √(2*a²) = a*√2. - Площадь квадрата тоже может быть выражена через длину диагонали, а так как каждая грань куба
имеет именно такую форму, знания площади грани (s) достаточно для вычисления ее диагонали (l). Площадь каждой боковой поверхности куба
равна возведенной в квадрат длине ребра, поэтому сторону квадрата грани можно выразить через нее как √s. Подставьте это значение в формулу из предыдущего шага: l = √s*√2 = √(2*s). - Куб составлен из шести граней одинаковой формы, поэтому, если в условиях задачи дана общая площадь поверхности (S), для вычисления диагонали грани (l) достаточно немного изменить формулу предыдущего шага. Замените в ней площадь одной грани одной шестой общей площади: l = √(2*S/6) = √(S/3).
- Длину ребра куба
можно выразить и через объем этой фигуры (V), а это позволяет формулу расчета длины диагонали грани (l) из первого шага использовать и в этом случае, внеся в нее некоторые поправки. Объем такого многогранника равен третей степени длины ребра, поэтому замените в формуле длину стороны грани кубическим корнем из объема: l = ³√V*√2. - Радиус описанной около куба
сферы (R) связан с длиной ребра коэффициентом, равным половине корня из тройки. Выразите сторону грани через этот радиус и подставьте выражение во все ту же формулу вычисления длины диагонали грани из первого шага: l = R*2/√3*√2 = R*√8/√3. - Формула расчета диагонали грани (l) с использованием радиуса вписанной в куб сферы (r) будет еще проще, так как этот радиус составляет половину длины ребра: l = 2*r*√2 = r*√8.
Диагональ куба — это один из элементов, который потребуется знать при решении заданий по стереометрии во время выполнения итоговой работы по математике за курс основной школы.
Немного теории о кубе
Этот многогранник относится сразу к прямым параллелепипедам и призмам. Он – частный случай того и другого. В основании куба лежит квадрат, и боковые ребра его равны стороне данного квадрата. Таким образом, все три измерения имеют одинаковые значения.
Все шесть граней куба представляют собой квадраты. Длина каждого из 12 ребер одинаковая.
В каждой из граней можно провести диагональ, длину которой легко найти по формуле Пифагора. Кроме того, сам куб имеет диагонали. Их всего четыре. Проводится диагональ куба так, чтобы начинаться из вершины нижнего основания. Конец этого отрезка оказывается в вершине верхнего основания, но так, чтобы не совпасть с диагональю квадрата.
Важные формулы
В них потребуется ввести одинаковое обозначение. Чаще всего буква «а» — это сторона куба. «V» приходится на объем. «S» и «d» соответственно площадь и диагональ. «R» и «r» радиусы описанной и вписанной сфер.
V= a³
(№1)
используется для нахождения объема;
S= a²
(№2)
формула для площади грани;
S= 6a²
(№3)
необходима для расчета площади всей поверхности куба;
если требуется узнать диагональ куба, формула будет такой d=
а
√
3 (№4);
для поиска радиусов пригодятся: R=
(а/2)*
√3
и
r=
а/2 (№5) и (№6)
.

Несколько слов о симметрии куба
У этого геометрического тела есть два вида симметрии: относительно точки и оси. Для нахождения первой потребуется провести диагональ куба, потом вторую, чтобы найти точку их пересечения. Она будет центром симметрии.
Все прямые, которые проходят через эту точку и являются перпендикулярными к граням, оказываются осями симметрии.
Примеры заданий из ЕГЭ
Они используются в части В, то есть там, где нужно выполнить развернутое решение задания. Просто выбрать ответ здесь не удастся. Поэтому придется знать формулы и уметь их применять в различных ситуациях.
Первая группа заданий.
В ней известна длина диагонали куба. Требуется вычислить его объем или узнать площадь поверхности.
К примеру, известная величина может быть равна единице. Тогда, чтобы узнать объем и площадь, нужно воспользоваться формулами № 1 и 3. Но в них идет речь о ребре, а дана диагональ. Потребуется записать еще одну формулу.
Если посмотреть на чертеж куба и проведенную в нем диагональ, то можно увидеть, что образуется прямоугольный треугольник. Один его катет совпадает с ребром, второй – с диагональю грани, а гипотенузой оказывается диагональ куба.
Тогда можно записать теорему Пифагора: квадрат гипотенузы (d 2) равен квадрату перового катета (а 2), сложенному с квадратом второго (а√2) 2 . После выполнения преобразований получается, что ребро куба а так связано с диагональю, что равно d, деленному на корень квадратный из 3.
Теперь можно начала узнать ребро, а потом подсчитать объем и площадь. В конкретной задаче а=1/√3=(√3)/3. Тогда объем получается равным (√3)/9. Площадь же — два.

Вторая группа заданий.
Обратная предыдущей, когда известны площадь или объем, а требуется вычислить значение диагонали куба.
Примером может служить задача, в которой известна площадь поверхности, и она равна 8. Необходимо будет воспользоваться формулой №3 и той зависимостью, которая выведена в предыдущей задаче.
Сначала потребуется узнать длину ребра. Она равна квадратному корню из частного S на 6. После подстановки известной величины а=√(8/6)=√(4/3). Теперь осталось вычислить диагональ куба, возведя это число в квадрат и умножив его на 3. Получится 2.
Третья группа заданий
содержит данные о диагонали грани куба. В них необходимо узнавать объем или площадь тела. Возможен также вариант, в котором потребуется вычислить диагональ самого куба. В таких задачах рассуждения идут тем же путем, который рассмотрен в предыдущих случаях.
