Как найти диагонали параллелограмма заданного векторами

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Векторная алгебра.
• Высшая математика.
• Векторная алгебра.
• Скалярное произведение векторов, свойства. Длина вектора. Угол между векторами.

Скалярное произведение векторов, свойства. Длина векторов. Угол между векторами.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Длина вектора.

Пусть вектор $overline a=(x, y, z)$ представлен своими координатами в прямоугольном базисе. Тогда его длину можно вычислить по формуле $$|overline a|=sqrt.$$

Скалярное произведение векторов.

Если заданы координаты точек $A(x_1, y_1, z_1) $ и $B(x_2, y_2, z_2),$ то координаты вектора $overline$ можно найти по формулам $$overline=(x_2-x_1, y_2-y_1, z_2-z_1).$$ Скалярным произведением ненулевых векторов $a_1$ и $a_2$ называется число $$(a_1, a_2)=|a_1||a_2|cos(widehat).$$

Для скалярного произведения наряду с обозначением $(a_1,a_2)$ используется также обозначение $a_1a_2.$

Геометрические свойства скалярного произведения:

1) $a_1perp a_2Leftrightarrow a_1a_2=0$ (условие перпендикулярности векторов).

2) Если $varphi=(widehat),$ то $$0leqvarphi 0; qquadqquad frac <pi>

Алгебраические свойства скалярного произведения:

2) $(lambda a_1)a_2=lambda (a_1 a_2);$

Если векторы $a_1(X_1, Y_1, Z_1)$ и $a_2(X_2, Y_2, Z_2)$ представлены своими координатами в прямоугольном базисе, то скалярное произведение равно $$a_1a_2=X_1X_2+Y_1Y_2+Z_1Z_2. $$

Из этой формулы, в частности, следует формула для определения косинуса угла между векторами:

Решение.

а) $$a_1^2=(a_1, a_1)=|a_1||a_1|cos(widehat)=|a_1|^2=3^2=9.$$

б) $(3a_1-2a_2)(a_1+2a_2);$

Поскольку скалярное произведение зависит от длин векторов и угла между ними, то заданные векторы можно выбрать произвольно учитывая эти характеристики. Пусть $a_1=(3; 0). $ Тогда вектор $a_2,$ имея длину $|a_2|=4,$ и, образуя угол $frac<2pi><3>$ с положительной полуосью оси $OX,$ имеет координаты $x=|a_2|cosfrac<2pi><3>=-frac<4><2>=-2; $

$3a_1-2a_2=3(3;0)-2(-2;2sqrt 3)=(9;0)-(-4; 4sqrt 3)=(13;-4sqrt 3);$

$a_1+2a_2=(3; 0)+2(-2;2sqrt 3) = (3; 0)+ (-4; 4sqrt 3)= (-1; 4sqrt 3).$

$(3a_1-2a_2)(a_1+2a_2)=(13; -4sqrt 3)(-1; 4sqrt 3) =-13-48=-61.$

в) $(a_1+a_2)^2.$

$a_1+a_2$=$(3; 0)+(-2; 2sqrt 3)=(1; 2sqrt 3).$

$(a_1+a_2)^2=(1; 2sqrt3) (1; 2sqrt 3)=1+12=13.$

Ответ: a) 9; б) -61; в) 13.

2.67. Вычислить длину диагоналей параллелограмма, построенного на векторах $a=p-3q, $ $b=5p+2q,$ если известно, что $|p|=2sqrt<2>, |q|=3, (widehat)=frac<pi><4>.$

Решение.

Способ 1.

Из треугольника $ABC$ имеем $AC=AB+BC=a+b=p-3q+5p+2q=6p-q.$

Зная длину векторов $p$ b $q$ и угол между этими векторами, можно найти длину вектора $AC$ по теореме косинусов:

Из треугольника $ABD$ имеем: $BD=AD-AB=b-a=5p+2q-p+3q=4p+5q.$

По теореме косинусов находим длину вектора $BD:$

$|BD|^2=|4p|^2+|5q|^2-8p5qcos widehat<(6p, q)>=$ $128+225+240=593.$

Пусть $q=(3; 0). $ Тогда вектор $p,$ имея длину $|p|=2sqrt 2,$ и образуя угол $frac<pi><4>$ с положительной полуосью оси $OX$ имеет координаты

Из треугольника $ABC$ имеем

Из треугольника $ABD$ имеем

$BD=AD-AB=b-a=5p+2q-p+3q=4p+5q=$ $=4(2; 2)+5(3;0)=(8; 8)+(15; 0)=(23; 8).$

Ответ: $15, sqrt <593>.$

2.68. Определить угол между векторами $a$ и $b$ если известно, что $(a-b)^2+(a+2b)^2=20$ и $|a|=1, |b|=2.$

Ответ: $2pi/3$

$|a_1|=3; |a_2|=5. $ Определить, при каком значении $alpha$ векторы $a_1+alpha a_2$ и $a_1-alpha a_2$ будут перпендикулярны.

Ответ: $alpha=pmfrac<3><5>$

В треугольнике $ABC$ $overline=3e_1-4e_2;$ $overline=e_1+5e_2.$ Вычислить длину его высоты $overline,$ если известно, что $e_1$ и $e_2$ взаимно перпендикулярные орты.

Как найти длины диагоналей параллелограмма заданного векторами

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет – тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку “Зарегистрироваться” вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.

Задача 32233 Определить длины диагоналей.

Условие

Определить длины диагоналей параллелограмма, построенного на векторах [b]a=2m+n[/b] и [b]b=m-2n[/b], где [b]m[/b] и [b]n[/b]-единичные векторы, угол между которыми 60 градусов.

Все решения

=(3vector-vector)^2=9vector*vector-6vectorvector+
vector*vector=9*1*1cos0^(o)-6*1*1*cos60^(o)+1*1*cos0^(o)=
=9-3+1=7
|vector|=sqrt(7)

=(vector+3vector)^2=vector*vector+6vectorvector+
9vector*vector=*1*1cos0^(o)+6*1*1*cos60^(o)+9*1*1*cos0^(o)=
=1+3+9=13
|vector|=sqrt(13)

[spoiler title=”источники:”]

http://reshka.feniks.help/vysshaya-matematika/analiticheskaja-geometrija/najti-ploshhad-i-dliny-diagonalej-parallelogramma-postroennogo-na-vektorah-a-b

http://reshimvse.com/zadacha.php?id=32233

[/spoiler]

Задача 1 Разложить вектор По векторам и .

Пусть , т. е. ;

След., вектор .

Задача 2 Найти длину диагонали параллелограмма, построенного на векторах , если

Рассм. диагонали параллелограмма ;

Вычислим ;

;

Задача 3 Показать, что точки Являются вершинами параллелограмма и найти проекцию одной из диагоналей на большую сторону параллелограмма.

Рассм.

, след. – параллелограмм (так как две противоположные стороны параллельны и равны);

Рассм. Рассм. ; ,

След. – большая сторона параллелограмма ; рассм. диагональ ;

Вычислим Вычислим ;

.

Задача 4 Длина гипотенузы прямоугольного треугольника равна . Вычислить

Задача 5 Найти момент силы, приложенной в точке относительно точки, а также модуль и направляющие косинусы вектора силы

1) , где ; ;

;

2) ;

Направл. косинусы вектора : ; ; .

Задача 6 Треугольник построен на векторах Найти длину высоты , если векторы взаимно перпендикулярны и по модулю равны

Рассм. векторы рассм. ;

;

;

;

Задача 7 Найти координаты вершины тетраэдра, если известно, что она лежит на оси , объём тетраэдра равен , .

Пусть искомая вершина тетраэдра (т. к. т. );

Рассм. в-ры: ;

Рассм. смешанное произв-е:

Рассм. объём тетраэдра : ; ; ;

; ; ; след., возможные положения искомой т.: ; .

Задача 8 В треугольнике известны координаты двух вершин: И точки пересечения медиан . Составить уравнение высоты треугольника, проведённой из вершины .

1) Определим координаты точки Как середины отрезка :;

2) Определим координаты вершины , используя равенство , где ;

Рассм.

;

3) составим ур-е высоты : рассм. в-р ;

Рассм. т. И рассм. в-р ; тогда по условию задачи и и, след., ур-е прямой , проходящей через Перпендикулярно в-ру , можно записать в виде: т. е. .

Задача 9 В параллелограмме известны уравнения сторон и координаты точки пересечения диагоналей Составить уравнения двух других сторон и диагоналей параллелограмма.

1) определим координаты точки как точки пересечения прямых :

;

2) определим координаты точки из условия, что т. – середина отрезка :

;

3) составим уравнение диагонали как прямой, проходящей через точки : ;

4) составим уравнение стороны как прямой, проходящей через точку параллельно

Прямой ;

5) составим уравнение стороны как прямой, проходящей через точку Параллельно

Прямой ;

6) определим координаты точки как точки пересечения прямых :

;

7) составим уравнение диагонали как прямой, проходящей через точки : .

Задача 10 Составить уравнение плоскости, проходящей через точки

Пусть – искомая плоскость; рассм. векторы ;

Рассм. норм. вектор ;

Рассм. произв. т. и рассм. вектор ;

, т. е. ;

Задача 11 Составить уравнение прямой , которая, проходит через точку и пересекает две прямые и .

Рассм. направл. векторы прямых ;

Рассм. т.; рассм. векторы ;

Пусть – плоскость, в которой лежат прямые ; пусть – плоскость, в которой лежат прямые ; тогда искомая прямая есть линия пересечения плоскостей ;

;

;

В качестве направл. вектора прямой можно взять вектор ; выберем ;

Запишем канонические ур-я прямой Как ур-я прямой, проходящей через т. А параллельно

Вектору : ; параметрические ур-я прямой :

Задача 12 Составить уравнение геометрического места всех прямых, проходящих через точку перпендикулярно прямой .

Запишем канонич. уравнения прямой в виде: ; её направл. вектор ;

Рассм. произв. прямую , удовлетв. условию задачи; рассм. произв. точку и её направл. вектор ; , т. е. ;

Плоскость и есть искомое геометрическое место.

Задача 13 Вычислить определитель третьего порядка, пользуясь определением; результат проверить разложением

Определителя по первой строке.

1) Непосредственное вычисление:

2) Разложение по 1-й строке:

Задача 14 Решить систему линейных уравнений по правилу Крамера и с помощью обратной матрицы:

Запишем данную систему уравнений в матричной форме: , (1) , где ; ; ;

Рассм. опред-ль матрицы : ,

След., матр. – невырожденная и можно применять формулы Крамера и вычислять обратную матр. ;

1) решим с – му ур – й (1) по правилу Крамера, т. е. с помощью формул: , , , где ;

;

;

; , , ;

реш–е с–мы ур–й (1) в коорд. форме: вектор–решение с-мы (1): ;

2) получим реш–е с–мы ур–й (1) с помощью обратной матр. :

, след., матр.– невырожденная и существует обратная матр. ;

Умножим рав-во (1) слева на матрицу : , ; вычислим обратную матр. :

Находим алгебр. дополнения для всех эл-тов матрицы и составим из них м-цу :

Транспонируем м-цу и получим «присоединённую» м-цу

Разделим все эл-ты присоедин. м-цы на опр-ль и получим обратную матр. :

Находим теперь вектор-решение :

Задача 15 Установить, являются ли векторы линейно зависимыми.

Вычислим ранг системы векторов методом Гаусса, т. е. выпишем матрицу их координат и приведём её к ступенчатому виду:

ранг матрицы , след. данная система векторов линейно независима.

Задача 16 Исследовать систему линейных уравнений на совместность и в случае совместности найти её решение методом Гаусса.

Выпишем расширенную матрицу данной системы ур-й и приведём её к ступенчатому виду:

имеем ;

Так как , то по теореме Кронекера – Капелли данная система уравнений совместна, а так как , то система имеет бесконечное множество решений; объявим свободной переменной и выпишем общее решение системы в координатной форме:

общее решение системы имеет вид:

Задача 17 Найти матрицу преобразования, выражающего Через , если

Запишем данные преобразования в матричной форме: , где матрицы и

Вектор – столбцы имеют вид:

Рассм. ;

Вычислим матрицу .

Задача 18 Найти собственные числа и собственные векторы линейного преобразования, заданного матрицей

1) Находим собств. значения линейного преобразования , т. е. корни характеристического уравнения :

Рассм.

– собств. значения (действ.) лин. преобр-я ;

2) находим собств. векторы линейного преобразования , соотв. собств. значениям :

А) рассм.

Рассм. Пусть , тогда вектор ;

Б) рассм.

Рассм.

Пусть , тогда , вектор ;

Пусть , тогда , вектор ;

След. собств. векторы линейного преобразования суть:

; ; .

< Предыдущая

Примеры решения задач

Задача 1.
Определить длины диагоналей параллелограмма,
построенного на векторах

и

,
где

таковы, что

.

Решение.
Диагонали параллелограмма есть векторы

и

.
Вычислим длину вектора

:

.

Аналогично
вычисляется длина вектора

.

Задача 2.
Найдите вектор

,
коллинеарный вектору

и удовлетворяющий условию

.

Решение.
Обозначим вектор

,
тогда из условий задачи

или

,

тогда

.
Итак:

.

Задача 3.
Найти проекцию вектора

на направление вектора

.

Решение.

.
По формуле проекции вектора на ось будет
иметь место равенство

.

Задача 4.
Даны векторы:

.

П
роверить,
есть ли среди них коллинеарные. Найти

.

Решение.
Условие коллинеарности имеет вид

.
Этому условию удовлетворяют векторы

.
Следовательно, они коллинеарны. Найдем
длины

векторов

:

.

Угол между векторами
определяется по формуле

.

Т

огда

,

.

Используя формулу

,
получим

.

Задача 5.
На материальную точку действуют силы

.
Найти работу равнодействующей этих сил

при перемещении точки из положения

в положение

.

Решение.
Найдем силу

и вектор перемещения

.

,
тогда искомая работа

.

Задачи

1. Векторы

взаимно перпендикулярны, а вектор

образует с ними углы

.
Зная, что

,
найти: 1)

;
2)

.

2. Вычислить длину
диагоналей параллелограмма, построенного
на векторах

,
если известно, что

.

3. Доказать, что
вектор

перпендикулярен к вектору

.

4. Зная, что

,
определить, при каком значении коэффициента

векторы

окажутся перпендикулярными.

5. Даны вершины
четырехугольника:

.
Доказать, что его диагонали взаимно
перпендикулярны.

6. Найти острый
угол между диагоналями параллелограмма,
построенного на векторах

.

7. Даны силы

.
Найти работу их равнодействующей при
перемещении точки из начала координат
в точку

.

8. Даны вершины
треугольника:

.
Найти проекцию вектора

на вектор

.

9. Найти вектор

,
перпендикулярный векторам

,
если известно, что его проекция на вектор

равна единице.

10. Сила, определяемая
вектором

,
разложена по трем направлениям, одно
из которых задано вектором

.
Найти составляющую силы

в направлении вектора

.

11. Даны вершины
треугольника:

.
Найти его внутренний угол при вершине
А и внешний угол при вершине В.

12. Даны три
последовательные вершины параллелограмма:

.
Найти его четвертую вершину D
и угол между векторами

.

13. На оси

найти точку, равноудаленную от точек

.

14. Доказать, что
треугольник с вершинами

прямоугольный.

Домашнее задание

1. Вычислить
скалярное произведение двух векторов

,
зная их разложение по трем единичным
взаимно перпендикулярным векторам

;

.

2. Найти длину
вектора

,
зная, что

– взаимно перпендику-

лярные орты.

3. Векторы

попарно образуют друг с другом углы,
каждый из которых равен

.
Зная, что

,
определить модуль вектора

.

4. Доказать, что
вектор

перпендикулярен к вектору

.

5. Даны векторы

,
совпадающие со сторонами треугольника
АВС. Найти разложение вектора, приложенного
к вершине В этого треугольника и
совпадающего с его высотой BD
по базису

.

6. Вычислить угол
между векторами

,
где

–
единичные взаимно перпендикулярные
векторы.

7. Даны силы

,
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда ее точка приложения,
двигаясь прямолинейно, перемещается
из положения

в положение

.

8. Даны вершины
треугольника

.
Определить его внутренний угол при
вершине В.

9. Вычислив
внутренние углы треугольника с вершинами

,

,
убедиться, что этот треугольник
равнобедренный.

10. Найти вектор

,
зная, что он перпендикулярен векторам

и

.

11. Найти вектор

,
коллинеарный вектору

и удовлетворяющий условию

,
где

.

12. Вычислить
проекцию вектора

на ось вектора

.

13. Даны векторы

.
Вычислить

.

14. Даны точки

.
Вычислить проекцию вектора

на ось вектора

.

Ответы к задачам

1) -7, 13. 2) 15,

.
4)

.
6)

.
7) 2. 8) -1/3.

9)

.
10)

.
11)

.

12)

.
13)

.

Ответы к домашнему
заданию

1) 9. 2) 5. 3) 10. 5)

.
6)

.
7) 13. 8)

.

10)

.
12) 6. 13) 5. 14) 3.

Занятие 3

Векторое
произведения векторов. Смешанное
произведение векторов

Определение1.
Тройка
некомпланарных векторов

называется правой (левой) если, находясь
внутри телесного угла, образованного
приведенными к общему началу векторами

и от него к

,
човершающимся против часовой стрелки
(по часовой стрелке)

Тройка правая
Тройка левая

Определение
2. Векторным
произведением вектора

на вектор

называется вектор

,
длина и направление которого определяются
условиями:

1.

,
где

– угол между

.

2.

.

3.

– правая тройка векторов.

Свойства
векторного произведения

1.

(свойство антиперестановочности
сомножителей);

2.

(распределительное относительно суммы
векторов);

3.

(сочетательное относиельно числового
множителя);

4.

(равенство нулю векторного произведения
означает коллинеарность векторов);

5.

,
т. е. момент сил равен векторному
произведению силы на плечо.

Если вектор

,
то

.

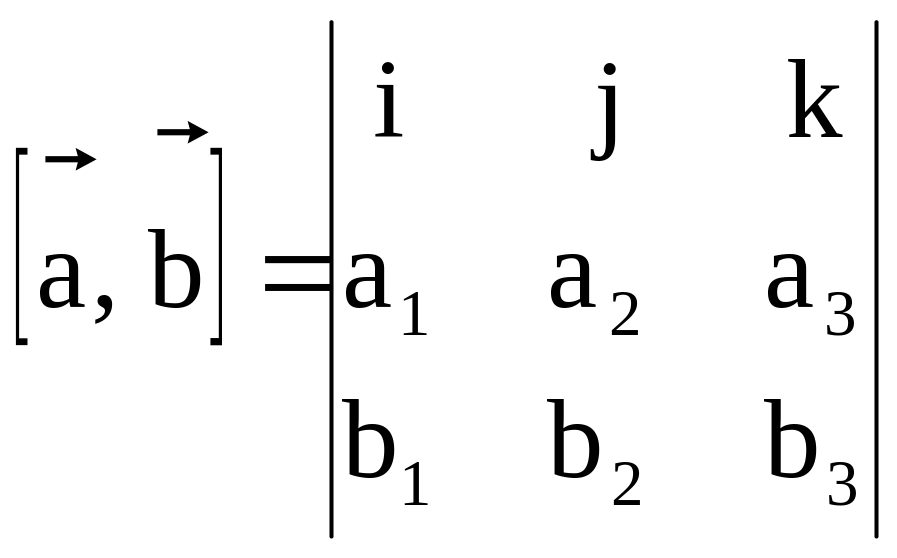
Определение
3. Смешанным
произведением

трех векторов называется число,
определяемое следующим образом:

.
Если векторы заданы своими координатами:

,
то

~

.

Свойства
смешанного произведения

1. Необходимым и
достаточным условием компланарности
векторов

является равенство

= 0.

2. Объем
параллелепипеда, построенного на
векторах

:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #