Как найти диагонали ромба через координаты

Очевидно, вершинами будут точки пересечения стороны и диагонали, другой стороны и диагонали.
Чтобы понять прямо по клеточкам нарисуй прямые сторон и диагнональки.
1. Реши 2 системы из 2 линейных уравнений. Первая x+2y=4 и y=x+2 даст одну вершинку ромба. (отметь на рисунке) .
Вторая x+2y=10 и y=x+2. (http://www.bymath.net/studyguide/alg/sec/alg15.html – пример нижний)
2. Отметь точки и проведи через них две параллельные прямые – найди координаты по графику 2 других вершин.

Я применила 2 метода и графический и алгебраический, т. к. не в курсе того какой раздел матики ты проходишь.

Еше можно: вторая диагональ ромба – это серединный перпендикуляр первой диагональки. Применить условие перпендикулярности прямых. найдешь угловой коэффициент = -1.
Найти координаты точки, делящей пополам первую диагональ.
Теперь по точке и угловому к-ту составишь уравнение второй диагонали.
И найди недостающие 2 вершины

Вопрос Составить уравнение диагонали ромба?, расположенный на этой странице сайта, относится к
категории Математика и соответствует программе для 10 – 11 классов. Если
ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска
похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему.
Для этого ключевые фразы введите в строку поиска, нажав на кнопку,
расположенную вверху страницы. Воспользуйтесь также подсказками посетителей,
оставившими комментарии под вопросом.

У этого термина существуют и другие значения, см. Ромб (значения).

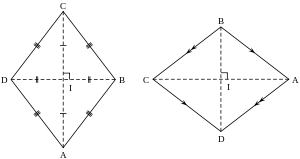
Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны^[1] (см. другие варианты определения).

Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Свойства[править | править код]

• Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны: АВ || CD, AD || ВС. Противоположные углы ромба равны, а соседние углы дополняют друг друга до 180°.
• Высоты в ромбе равны между собой.
• Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре конгруэнтных прямоугольных треугольника.
• Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
• Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
• Середины четырёх сторон ромба являются вершинами прямоугольника.
• Диагонали ромба являются осями его симметрии.
• В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Признаки[править | править код]

Самое общее определение: ромб — это выпуклый четырёхугольник^[2], все стороны которого равны друг другу. Можно показать, что такой четырёхугольник является параллелограммом^[3][1].

Параллелограмм является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий^[4]:

• Две его смежные стороны равны (отсюда следует, что все стороны равны).
• Его диагонали пересекаются под прямым углом.
• Одна из диагоналей делит содержащие её углы пополам. Другими словами, диагональ является биссектрисой противоположных углов.
• Диагонали параллелограмма делят его на четыре равных между собой треугольника.
• Диагонали параллелограмма являются осями симметрии^[5].

Помимо всего, ромб можно рассматривать как частный случай дельтоида, у которого любые две смежные стороны равны между собой.

Квадрат как частный случай ромба[править | править код]

Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.

Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов^[6][7].

Уравнение ромба[править | править код]

Уравнение ромба с центром в точке и диагоналями, параллельными осям координат, может быть записано в виде^[8]:

где — половины длин диагоналей ромба по осям соответственно.

Длина стороны ромба равна Площадь ромба равна Левый угол ромба рассчитывается по формуле:

Второй угол дополняет его до 180°.

В случае a = b уравнение отображает повёрнутый на 45° квадрат:

где сторона квадрата равна а его диагональ равна Соответственно площадь квадрата равна

Из уравнения видно, что ромб можно рассматривать^[8] как суперэллипс степени 1.

Площадь ромба[править | править код]

• Площадь ромба равна половине произведения его диагоналей.

• Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.

• Кроме того, площадь ромба может быть вычислена по формуле:

,

где  — угол между двумя смежными сторонами ромба.

• Также площадь ромба можно рассчитать по формуле, где присутствует радиус вписанной окружности и угол :

• Площадь ромба равна удвоенному произведению стороны и радиуса вписанной окружности:

Радиус вписанной окружности[править | править код]

Радиус вписанной окружности r может быть выражен через диагонали p и q в виде^[9]:

В геральдике[править | править код]

Ромб является простой геральдической фигурой.

• 

  Червлёный ромб в серебряном поле

• 

  В червлёном поле 3 сквозных ромба: 2 и 1

• 

  Просверленный червлёный ромб в серебряном поле

• 

  В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

Симметрия[править | править код]

Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.

• 

  Ромбический орнамент

• 

  Ромбические звёзды

• 

  Более сложный орнамент

• 

См. другие примеры на Викискладе.

См. также[править | править код]

• Дельтоид
• Звезда (геометрия)
• Ромбододекаэдр
• Ромбоид

Примечания[править | править код]

Литература[править | править код]

• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.

Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: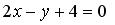 и и уравнение одной из его диагоналей: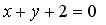 . Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой 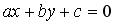определяется по формуле:

.

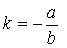
Стороны параллельны, так как имеют одинаковый угловой коэффициент:

.

Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:

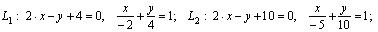
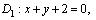
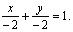
Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:

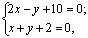
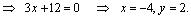
Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка 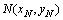является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :

.

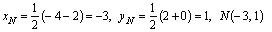
3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору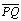. Найдем его координаты:

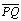= — 2 — (- 4); 0 — 2 = {2; — 2}.

По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору 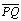= {2; — 2}:

2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.

4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:

, , , .

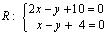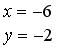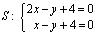Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4).

Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:

h : 3 x + y + 11 = 0, m : x + 2 y + 7 = 0 ,

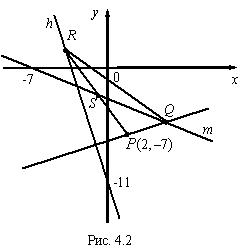
План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h :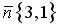. Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору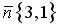, запишем в виде:

, x — 3 y — 23 = 0 .

Находим координаты точки Q — точки пересечения прямых PQ и m :

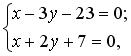x = 5 , y = — 6.

2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:

, .

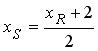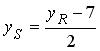Точка S лежит на медиане m , значит,

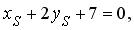
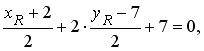
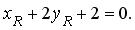
Точка R лежит на высоте h , значит,

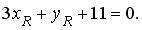
Из последних двух уравнений определяем координаты точки R , решая систему:

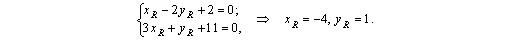
3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P :

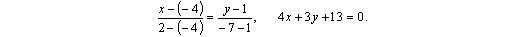
Аналогично, составим уравнение прямой RQ :

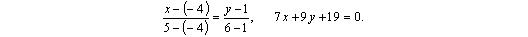
Ответ: x — 3 y — 23 = 0, ,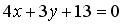

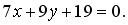
Диагонали ромба онлайн

1. Диагонали ромба через высоту и угол

Пусть известны высота и угол ромба (Рис.1).

Покажем, что диагонали ромба через высоту и угол вычисляются по формулам

Формула стороны ромба через высоту и угол имеет следующий вид:

Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то треугольник AOB прямоугольный. Тогда из теоремы синусов, имеем:

или, учитывая (small AO=frac{large d_1}{large 2} ,) (small BO=frac{large d_2}{large 2} ,) ( small AB=a ,) ( small sin(90°-frac{alpha}{2})=cos frac{alpha}{2} ,) получим

Подставляя (3) в (4) и (5), и учитывая формулу синуса двойного угла ( small sin alpha=2sin frac{alpha}{2}cos frac{alpha}{2} ,) получим:

Мы вывели формулы диагоналей ромба (1) и (2) через высоту и угол.

2. Диагонали ромба через площадь и высоту

Рассмотрим ромб с высотой h и площадью S (Рис.2).

Покажем, что диагонали ромба через высоту и площадь вычисляются по формулам:

где

В параграфе 1 мы вывели формулы длин диагоналей (6), (7) через высоту и угол. Покажем, что угол ромба через площадь и высоту вычисляется формулой (8).

В статье Сторона ромба мы вывели формулы стороны ромба через площадь и высоту, а также через высоту и угол:

Сравнивая (9) и (10), получим:

Откуда:

или

Заметим, что высота ромба не может быть больше стороны ромба ( ( small h≤a ) ) и, следовательно, ( small h^2≤acdot h=S .)

3. Диагонали ромба через площадь и угол

Выведем формулу вычисления диагоналей ромба через площадь и угол. В статье Площадь ромба были выведены формулы площади ромба через угол и противолежащую диагональ и через угол и диагональ из данного угла:

Из (11) и (12) найдем ( small d_1 ) и ( small d_2: )

4. Диагональ ромба через угол и противолежащую диагональ

Пусть известна один из углов α=∠ABC ромба и противолежащая диагональ d₁=AC (Рис.4). Выведем формулу вычисления диагонали d₂=BD ромба.

Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Кроме этого, диагонали ромба делят углы ромба пополам. Для прямоугольного треугольника AOB, имеем:

Откуда, учитывая, что (small AO=frac{large d_1}{large 2}, ) (small BO=frac{large d_2}{large 2}, ) получим формулу диагонали ромба через угол и противолежащую диагональ:

или

5. Диагональ ромба через угол и диагональ из данного угла

Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d₂=BD (Рис.5). Выведем формулу вычисления диагонали d₁=AC ромба.

Из формулы (15) найдем d₁:

или

6. Диагонали ромба через сторону и угол

Пусть известны сторона ромба и угол (Рис.6). Найдем диагонали ромба.

В статье Сторона ромба мы вывели формулу стороны ромба через угол и противолежащую диагональ, а также формулу стороны ромба через угол и диагональ из данного угла:

Из формул (17) и (18) найдем d₁ и d₂:

Получили формулы диагоналей ромба через угол и сторону ((19),(20)).

7. Диагонали ромба через площадь и радиус вписанной окружности

Пусть известны площадь ромба и радиус впианной в ромб окружности (Рис.7). Найдем диагонали ромба.

В параграфе 2 мы вывели формулы диагоналей ромба через площадь и высоту. Учитывая, что высота ромба равна радиусу вписанной в ромб окружности, умноженная на 2 (( small h=2r )), формулы (6)−(8) примут следующий вид:

где

Получили формулы длин диагоналей ромба через площадь и радиус вписанной окружности.