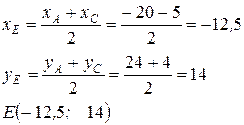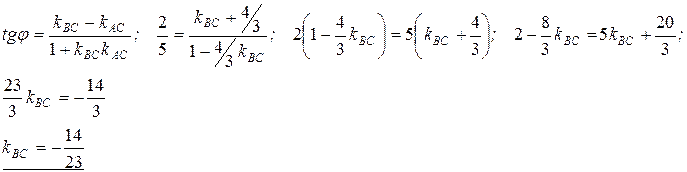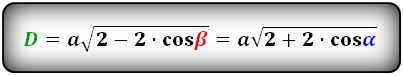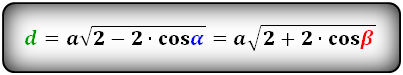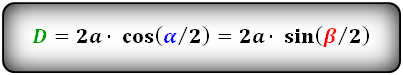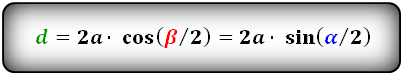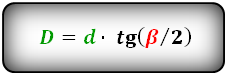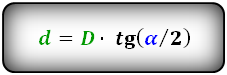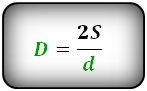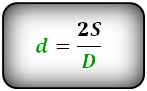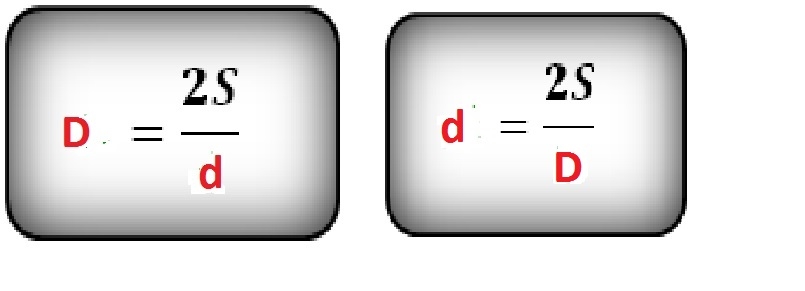Как найти диагонали ромба если известны вершины

Уравнение ромба в декартовой системе координат

Составление и решение уравнений многоугольников

Скачать:

Вложение	Размер
составление и решение уравнений многоугольников	124.82 КБ

Предварительный просмотр:

Автор работы: Шпакова Маргарита Андреевна, г.о. Тольятти, МБУ СОШ

Научный руководитель: Владимирова Ольга Ивановна, учитель математики первой категории МБУ СОШ № 58.

В школьном курсе математики учащиеся часто встречаются с алгебраическими уравнениями, уравнениями прямых, уравнениями окружностей, квадратными уравнениями и т.д. Что собой представляют уравнения многоугольников, учащиеся не знают.

Как, например, выглядит уравнение треугольника? Можно ли по фигуре на плоскости составить уравнение? Можно ли рассчитать площадь фигуры по заданному уравнению? Можно ли по заданному уравнению определить, что за многоугольник? Решение этих вопросов меня и заинтересовало. В них есть проблема моей исследовательской работы.

Цель работы: изучить и исследовать на примерах методы, которые дают возможность получить уравнение с модулем любого выпуклого многоугольника на плоскости, координаты вершин которого известны. Найти взаимосвязь площади фигуры от ее уравнения.

Основные ЗАДАЧИ исследования:

1. Познакомиться с некоторыми видами уравнений прямых на плоскости (уравнение прямой в отрезках, уравнение прямой, проходящей через две различные точки на плоскости);
2. Научиться составлять уравнение прямой через заданную точку и параллельную другой прямой;
3. Научиться составлять уравнение прямой, проходящей через две заданные точки;
4. Научиться по уравнению строить многоугольник на плоскости и наоборот, по чертежу составлять уравнение многоугольника;
5. Изучить метод областей при решении уравнений, содержащих знак модуля.

Как известно из курса геометрии, любая прямая на координатной плоскости может быть задана уравнением вида

Подобное уравнение называют линейным. Уравнение такого вида называют также общим уравнением прямой на плоскости.

Если ax+by+c = 0 – уравнение некоторой прямой m, то уравнение ax+by+c = p, где р ≠ 0, задает прямую m`, параллельную m. Это следует из того, что данные два уравнения не имеют общих решений, а значит, прямые не имеют общих точек.

У параллельных прямых

Пример1 . Составим уравнение прямой, проходящей через точку М (1;-2) и параллельной прямой 3x-4y+5=0

Подставляя координаты точки М в левую часть уравнения, получаем значение 16. Значит, искомым уравнением прямой будет 3x+4y+5=16 или окончательно 3x+4y-11=0.

Пусть известны координаты двух точек М 1 (x 1 ;y 2 ), М 2 (x 2 ;y 2 ), лежащих на данной прямой. Составим уравнение прямой, проходящей через две заданные точки:

(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0

Пример 2 . Составим уравнение прямой, проходящей через точку М 1 (3;1) и М 2 (2;2).

Получаем такое уравнение (x-3)(2-1)-(y-1)(2-3)=0

после преобразований выходит х+у-4=0.

Если известны координаты (а;0) и (0;b) точек пересечения прямой с осями Ох и Оу, то для этой прямой проще всего записать уравнение в отрезках + = 1.

Рассмотрим на координатной плоскости ху треугольник с вершинами в точках А (х 1 ;у 1 ), В (х 2 ;у 2 ), С (х 3 ;у 3 ). Уравнение прямой, на которой лежит сторона АВ этого треугольника, можно записать в виде

(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0.

Подставим координаты третьей вершины С (х 3 ;у 3 ) в левую часть этого уравнения,

получим некоторое значение

q=(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )

Чтобы понять геометрический смысл числа q, заметим, что уравнение

(х-х 1 )(у 2 -у 1 )-(у-у 1 )(х 2 -х 1 )=q задает прямую, параллельную стороне АВ данного треугольника. Поэтому для каждой точки этой прямой результат подстановки ее координат в левую часть уравнения тот же, что и для точки C (х 3 ;у 3 ), и дает число q. Значит, то же значение получится и для точки С 1 (х 4 ;у 1 ) пересечения упомянутой прямой с прямой у=у 1 , параллельной оси абсцисс и проходящей через вершину A треугольника. Но в этой точке

(х-х 1 )(у 2 -у 1 )-(у-у 2 )(х 2 -х 1 ) = (х 4 -х 1 )(у 2 -у 1 ). Геометрический смысл последнего выражения понять уже несложно: |(х 4 -х 1 )(у 2 -у 1 )| площадь параллелограмма со сторонами АВ и АС 1 . Длина стороны АС 1 равна |х 4 -х 1 |, а длина высоты параллелограмма, опущенной из вершины B на эту сторону, есть |у 2 -у 1 |. Поэтому |q| есть площадь ΔАВС 1 , но она такая же, что и у ΔАВС. В результате приходим к следующей формуле для площади треугольника

S = |(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )|. (3, стр. 169).

Если треугольник задан в декартовой системе координат и имеет своими вершинами точки А (х 1 ;у 1 ), В (х 2 ;у 2 ), С (х 3 ;у 3 ), то можно составить уравнение треугольника:

|(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )| + |(x-x 2 )(y 3 -y 2 )-(y-y 2 )(x 3 -x 2 )| +

+ |(x-x 3 )(y 1 -y 3 )–(y-y 3 )(x 1 -x 3 )| = 2S, где

S = |(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )|.

Пример 3 . Составим уравнение треугольника, изображенного на рисунке. Для этого составим уравнения прямых, которые являются его сторонами, по формуле

(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0, задающей уравнение прямой по двум ее точкам. При этом допустимым считаем раскрытие скобок и приведение подобных слагаемых и недопустимым – умножение обеих частей уравнения на некоторое число (за исключением -1) .

Уравнения сторон имеют вид: х-у+1=0, х+у-1=0, 2у=0. Сложив модули левых частей этих уравнений, и приравняв полученное выражение к удвоенной площади ΔАВС, равной в данном случае 1, приходим к искомому уравнению |x-y+1|+|x+y-1|+2|y|=2.

Описанный метод дает возможность получить уравнение любого выпуклого многоугольника на плоскости, координаты вершин которого известны.

Уравнение квадрата, ромба

Пример 4 . Составить уравнение квадрата:

|x-1| + |y-1| + |x| + |y| = 1. Площадь равна 1.

Пример 5 . Составить уравнение ромба:

Через точки с координатами (1;0), (0;1) уравнение прямой: x +y -1 = 0.

Через точки с координатами (-1;0), (0;1) уравнение прямой: x – y + 1 = 0.

Через точки с координатами (-1;0), (0;-1) уравнение прямой: x + y + 1 = 0.

Через точки с координатами (0;-1), (1;0) уравнение прямой: -x + y + 1 = 0.

Получили: | x + y – 1| + | x – y + 1| + | x + y + 1| + | -x + y + 1 | = 4.

Этот же ромб имеет другое уравнение: |х| + |у| = 1, которое лучше решать «методом областей». Площадь ромба равна 2.

Пример 6 . Докажите, что уравнения: |x + y| + |x – y| = 2 и |x + 1| + |y + 1| + |x -1| +|y – 1| =4 относятся к одному квадрату.

Первое уравнение лучше решать «методом областей», где вся плоскость разбивается прямыми у =-х и у=х на четыре области, значит, искомая фигура четырехугольник, стороны которого параллельны осям координат. Из уравнений каждой области у=1, х=1и т.д. понимаем, что это квадрат, площадь которого равна 4.

Второе уравнение наглядно изображено, подтверждая первое.

Пример 7. Определить вид многоугольника по уравнениям:

|х| + 3|у| = 6; |х-3| + |у+3| = 3; |х-1| + 7|у| = 1.

Во всех случаях даны уравнения ромба .

Пример 8 . Изобразить на плоскости многоугольник по данному уравнению: |x|+|y|+|x+y|=4.

Из данного уравнения следует, что х=0, у=0, х= -у –прямые, которые разбивают плоскость на несколько областей.

Найдем уравнение прямой, стороны многоугольника, в каждой из областей:

Проанализируем расположение квадрата на координатной плоскости.

В общем случае уравнение квадрата в декартовой (прямоугольной) системе координат принимает вид:

где точка О`(a;b) – точка пересечения диагоналей квадрата;

d – длина диагонали квадрата.

В частном случае, когда точка О(0;0) – начала координат, является одновременно и точкой пересечения диагоналей квадрата, уравнение квадрата принимает вид:

где d– длина диагонали квадрата.

Одно из уравнений квадрата можно записать так
|x| + |y| = a
обычно так рисуют ромб, но это квадрат

Вопрос:
Как выглядит уравнение квадрата, если его положить на сторону? Иными словами, стороны квадрата должны быть параллельны осям координат.

б) уравнения сторон AB, BC, CD и DA

Сделайте чертеж.

Решение.

1. Найдем уравнение прямой, на которой лежит AC – вторая диагональ квадрата. Вспомним, что уравнение любой невертикальной прямой может быть приведено к виду y=kx+b, где параметр k – угловой коэффициент этой прямой.

В силу свойства 1) диагоналей квадрата угловые коэффициенты k_AC и k_BD прямых AC и BD связаны соотношением:

Найдем угловой коэффициент k_BD. Для этого выразим y через x из данного уравнения прямой BD:

Итак, . Поэтому из соотношения (1) получим, что k_АС=3.

Теперь уже легко найти уравнение прямой AC. Нам известны координаты её точки А и угловой коэффициента k_AC. Используем уравнение прямой, проходящей через данную точку в данном направлении:

.

Подставим в это уравнение числовые данные нашей задачи: х_А=-3, у_А=2, k_АС=3. Получим: или (после упрощений)

2. С помощью свойства 2) диагоналей квадрата найдем координаты центра Е квадрата – точки пересечения его диагоналей.

Поскольку точка Е лежит на диагонали АС, её координаты удовлетворяют прямой АС; аналогично рассуждая, получим, что координаты точки Е должны одновременно удовлетворять и уравнению прямой BD. Таким образом, координаты точки Е должны удовлетворять системе из уравнений прямых АС и BD

(первое – уравнение прямой BD, второе – прямой АС). Далее, почленно вычитая первое уравнение из второго, получим:

, значит

Подставим найденное значение х в любое из уравнений системы, например, в первое. Найдем, что у=5.

Итак, мы нашли координаты точки Е, центра квадрата: -2 5, то есть Е(-2; 5).

3. Найдем длину отрезка АЕ – половину диагонали квадрата, а затем воспользуемся тем, что и остальные вершины квадрата находятся от его центра на таком же расстоянии (свойства 2) и 3) диагоналей), т.е. что все вершины квадрата лежат на окружности радиуса АЕ с центром в точке Е.

Подставив в правую часть этой формулы числовые значения координат точек А и Е, получим, что

.

Уравнение окружности радиуса АЕ с центром в точке Е записывается в виде:

.

Подставив в него числовые значения радиуса АЕ и координат центра Е, получим уравнение окружности, проходящей через все вершины квадрата:

.

Теперь с помощью простого рассуждения находим по очереди координаты всех вершин квадрата.

Точки А и С лежат на пересечении найденной нами окружности и прямой АС, это общие точки указанных окружности и прямой. Значит, координаты этих точек – решения системы уравнений окружности и прямой:

.

Координаты вершины А мы знаем, поэтому будем искать вершину С.

Подставим во второе уравнение системы вместо у его выражение 3х+11 из первого уравнения. Получим:

,

откуда , поэтому , т.е. , значит . Если квадрат числа равен 1, это число равно либо 1, либо -1. Поэтому и тогда , либо и тогда .

Во втором случае мы получили известную нам абсциссу вершины А (а из первого уравнения системы получим ординату этой вершины), а первый случай дает нам абсциссу вершины С: . Итак, найдена вершина С(-1; 8).

Аналогично, для нахождения координат вершин B и D надо решить систему, состоящую из уравнений прямой BD и той же окружности:

.

Итак, получены два решения системы, пара (1; 4) и (-5; 6). Одно из этих решений – координаты точки B, а второе – точки D. Поскольку обе эти вершины совершенно равноправны, мы можем любую из них обозначить буквой B, тогда вторая будет вершиной D. Вся разница в том, идут ли вершины A, B, C и D в порядке обхода контура квадрата по или против часовой стрелки, что для решения нашей задачи безразлично; просто надо выбрать одно из этих направлений произвольно.

Мы будем считать, что вершины квадрата таковы: B(1; 4); D(-5; 6).

4. Нам осталось найти уравнения сторон квадрата. Для этого вспомним уравнение прямой, проходящей через точки и :

(2)

и подставим в него координаты соответствующих вершин квадрата.

Уравнение прямой AB получим, если в формулу (2) вместо точек M и N возьмем точки A и B:

.

Подставляя в это уравнение координаты вершин А(-3; 2) и B(1; 4), находим:

откуда .

Аналогично получаем уравнения других сторон. Теперь можно сделать чертеж – Рис. 1.

Задача 3

В ромбе ABCD известны координаты вершин А и С и тангенс внутреннего угла С. Найти уравнения диагоналей и сторон, координаты двух других вершин, а также площадь этого ромба. Сделать чертёж. А(-20; 24); С(-5; 4); tgC= 20 /₂₁.

Изобразим графически положение ромба в прямоугольной системе координат Оху:

1) Запишем уравнение диагонали АС как уравнение прямой, проходящей через две заданные точки:

2) Так как в ромбе его диагонали взаимно перпендикулярны, то угловой коэффициент диагонали BD будет равен:

Определим координаты точки пересечения диагоналей ромба Е. Итак, Е – середина АС.

Запишем уравнение диагонали BD как уравнение прямой, проходящей через заданную точку Е в направлении, определяемом угловым коэффициентом.

3) Чтобы найти уравнения сторон ромба надо определить угловые коэффициенты k_AB=k_CD и k_BС=k_АD прямых на которых эти стороны лежат. Так как диагонали ромба делят его углы пополам, то положив С=2φ из формулы

, где tg2φ= 20 /₂₁ найдём tgφ.

Итак, tgφ=-2,5 – не удовлетворяет условию задачи, что угол φ – острый, поэтому tgφ=0,4.

· угол φ является углом между прямыми ВС и АС, то есть:

· угол φ является углом между прямыми DС и АС, то есть:

Так как противоположные стороны ромба параллельны, то определим угловые коэффициенты всех его сторон:

4) Вершины ромба В и D являются точками пересечения его соответствующих сторон АВ и ВС; СD и АD. Решим системы уравнений этих сторон.

В(-16,5; 11)

D(-8,5; 17)

Задача 1

Пусть точка А(-7; 3) – вершина квадрата ABCD, а его диагональ BD расположена на прямой 2х+у+6=0. Найдите:

в) координаты вершин B, C и D;

г) уравнения сторон AB, BC, CD и DA.

Задача 2

В ромбе ABCD известны координаты вершин А и С и тангенс внутреннего угла С. Найти уравнения диагоналей и сторон, координаты двух других вершин, а также площадь этого ромба. Сделать чертёж. А(5; 6); С(21; 18); tgC= 4 /₃.

Задача 3

Даны координаты вершин треугольника АВС. Написать уравнения окружностей вписанной и описанной около данного треугольника. А(11; 5); В(5; -3); С(-4; -3).

[spoiler title=”источники:”]

http://lektsii.org/6-85864.html

[/spoiler]

Диагональ параллелограмма – это отрезок, соединяющий противоположные вершины фигуры. В зависимости от
вида геометрической фигуры диагональ обладает важными свойствами, на которые основываются базовые
правила и формулы. Рассмотрим подробнее, как найти длину данного отрезка, построенного в
параллелограмме с равными сторонами, т.е. ромбе.

Диагональ ромба через сторону и другую известную диагональ

В случае, если в ромбе известны значения одной диагонали (d) и стороны (a) фигуры, прийти к
определению длины второго отрезка будет несложно, благодаря тождеству параллелограмма, которое
гласит, что сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:

d = √(4a² — d²)

где a — сторона, d — известная диагональ.

Пример. Дан ромб с диагональю равной 6 мм и стороной, длина которой 5 мм. Нужно
найти вторую диагональ ромба. d = √(4 * 5² — 6²) = √(4 * 25 — 36) = √(100 — 36) = √64 = 8 мм
– длина неизвестной диагонали.

Как найти длину большей диагонали через сторону и острый угол

Найти величину длинной диагонали можно по формуле:

d = a * √(2 + 2 * cos α)

где a — сторона, cos α — острый угол.

Проведенный отрезок, который соединяет противоположные вершины фигуры, делит ее на равнобедренные
треугольники. По свойствам равнобедренного треугольника косинус углов при основании равен половине
основания (в данном случае диагонали), деленного на боковую сторону (сторону ромба).

Пример. Острый угол между сторонами ромба длиной 6 см равен 45 градусам. Найти
биссектрису острого угла ромба (в данном случае диагональ). d = 6 * √(2 + 2 * cos 45°) = 6 * √(2 + 2 * √2 / 2) = 6 * √(2 + 2 * 0,7) = 11см
– длинна неизвестного отрезка.

Как найти длину большей диагонали через сторону и известное значение тупого угла

Как уже известно, построенная диагональ в ромбе, делит его на 2 равнобедренных треугольника. Если
дополнить картину второй проведенной диагональю, получится прямоугольный треугольник. Косинус
половинки тупого угла (c) это отношение прилежащего катета к гипотенузе (стороне ромба a). На
основании всех этих свойств можно прийти к простой формуле нахождения нужной диагонали через сторону
ромба (в данном случае гипотенузу) и косинус тупого угла:

d = a * √( 2 — 2 * cos β)

где a — сторона, cos β — тупой угол

Пример. Дан ромб со стороной 4,65 м, величина тупого угла которого равна 120
градусам. Необходимо найти противолежащую известному углу диагональ. d = 4,65 * √(2 — 2 * cos 120°) = 4,65 * √(2 — 2 * (-0,5) = 8 м
– длина неизвестного отрезка.

Как вычислить длину меньшей диагонали через сторону и острый угол

Так как ситуация аналогична предыдущей (только известный противолежащий угол острый), формула
нахождения короткой диагонали практически ничем не отличается от алгоритма определения длинного
отрезка, соединяющего противолежащие вершины ромба.

d = a * √(2 — 2 * cos α)

где a — сторона, cos α — острый угол

Пример. В ромбе со стороной 4,65 м проведена диагональ, которая является основанием
равнобедренного треугольника с углом при вершине равным 52 градусам. Найти основание треугольника
(меньшую диагональ). d = 4,65 * √(2 — 2 * cos 52°) = 4 м.

Короткая диагональ ромба через длинную диагональ и острый угол

Аналогично с предыдущей ситуацией, через тангенс острого угла находим величину неизвестного катета
(половинку искомой диагонали). Упрощенная формула:

d = D * tg (α / 2)

где D — длинная диагональ, α — острый угол

Пример. Острый угол ромба, в котором построена диагональ длиной 11 мм, равен 58
градусам. Найти длину второй диагонали. d = 11 * tg 29° = 6 мм – длина
меньшей диагонали ромба.

Короткая диагональ через сторону и тупой угол

Формула для нахождения меньшей диагонали ромба при помощи значения стороны и тупого угла такова:

d = a * √(2 + 2 * cos β)

где a — сторона, cos β — тупой угол

Пример. Дан ромб со стороной 4,65 мм, один из углов которого равен 128 градусов, а
меньшая диагональ фигуры – искомая величина. d = a * √(2 + 2 * cos β) = 4,65 *  √(2 + 2 * cos 128°) = 4 мм.

Длинная диагональ ромба через короткую диагональ и тупой угол

Длина большей диагонали ромба легко находится по формуле:

D = d * tg (β / 2)

где d — короткая диагональ, β — тупой угол

Благодаря теореме Пифагора, зная длину короткой диагонали (половина катета прямоугольного
треугольника) и значение тупого угла ромба (половина которого является углом прямоугольного
треугольника), не составит труда определить значение большей диагонали ромба через тангенс тупого
угла.

Пример. Дан ромб с диагональю 6,5 см, которая является биссектрисой тупого угла
величиной 119 градусов. Нужно найти неизвестную диагональ ромба. D = 6,5 * tg (119 / 2) = 11 см
– искомая величина.

Диагональ ромба через площадь и другую известную диагональ

Найти любую из двух диагоналей ромба можно по формуле:

D = 2 * S / d

где d – длина известного отрезка, а S-площадь фигуры.

Пример. Дан ромб с площадью равной 64 см², его диагональ равна 8,5 см. Необходимо
найти длину второго отрезка, соединяющего противолежащие вершины. D = 2 * S / d = 2 * 64 / 8,5 = 15 см.

Ромб относится к плоским выпуклым геометрическим фигурам. Данный вид параллелограмма отличается
равными сторонами, а также тем, что его диагонали при пересечении перпендикулярны друг другу.
Существуют и другие свойства ромба, которые подробно раскрывают смысл указанных выше формул:

• Диагонали, пересекаясь под прямым углом, делятся точкой пересечения пополам. Таким образом, они
  всегда разделяют фигуру на 4 прямоугольных треугольника.
• Противоположные стороны ромба попарно параллельны.
• Противолежащие углы равны, а смежные – в сумме образуют 180 градусов.
• Диагонали служат биссектрисами всех углов ромба.
• Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
• Если соединить середины сторон ромба, получится прямоугольник.
• Точка пересечения диагоналей — центр вписанной окружности.

Определение диагонали ромба часто встречается в задачах школьной программы. Найдя данное значение,
можно прийти к искомому результату задания. Через диагональ можно найти стороны ромба, площадь,
периметр и все внутренние углы ромба.

Геометрия в школьной программе включается в себя немалое количество формул, основанных на теоремах и
правилах. Некоторые из которых помогают значительно сократить время для решения задач на контрольной
или при выполнении домашней работы. Данная статья поможет быстро прийти к логическому решению
задания и правильному результату. Знание и применение выше перечисленных формул способствуют умению
решать задачи по геометрии любой сложности.

Как найти диагональ ромба

Ромб – четырехугольник, стороны которого равны и попарно параллельны. В отличие от квадрата, углы у которого прямые, ромб имеет по два острых и два тупых угла, лежащих на противоположных сторонах. А вот диагонали пересекаются под прямым углом и являются одновременно биссектрисами. Точка пересечения диагоналей делит их на равные части.

Формул для нахождения диагоналей ромба много, необходимо лишь знать исходные данные и подобрать подходящую.

1

Как найти диагональ ромба через сторону и угол: когда известны стороны и один из углов ромба, применяют следующие формулы:

2

Через сторону и половинный угол:

3

Через сторону и другую диагональ:

Сумма квадратов диагоналей равна квадрату стороны, умноженному на четыре D^2+d^2=4a^2. Отсюда можно вывести, что:

4

Через угол и другую диагональ:

5

Через площадь и другую диагональ: традиционной формулой для нахождения площади ромба считается S=a*h. Но относительно диагоналей она будет выглядеть S=1/2*D*d. После преобразований получаем:

6

Через периметр и другую диагональ. В этом случае формулу выведем самостоятельно. Т.к. ромб имеет равные стороны, чтобы найти одну из них, периметр делим на 4: a=P/4. Диагонали перпендикулярны друг другу и образуют прямой угол. Тогда одна из сторон и половины длин диагоналей образуют прямоугольный треугольник. Далее воспользуемся теоремой Пифагора. Для большой диагонали она будет выглядеть: D=2*(a^2-(d/2)^2)^1/2. Аналогично для нахождения малой диагонали: d=2*(a^2-(D/2)^2)^1/2.

Пример:

Найти меньшую диагональ ромба, если периметр равен 20 см, большая диагональ равна 8 см.

Дано: Р=20см, D=8 см. Найдем длину одной стороны ромба, разделив периметр на четыре a=20/4=5 см. Воспользуемся формулой пункта №3 и получим d=(4*5^2-8^2)^1/2=6 см.

Несмотря на кажущуюся простоту такой геометрической фигуры, как ромб, он таит в себе много интересных моментов. К нему применимы свойства параллелограмма, биссектрисы, прямоугольного, а иногда и равнобедренного треугольника. Зная формулы, легко можно решить задачи по нахождению диагоналей ромба.