как найти диагонали в правильном шестиугольники? как найти диагонали в правильном шестиугольники?
Ученик
(229),
закрыт
11 лет назад
Владимир
Мастер
(1589)
11 лет назад
Диагональ правильного шестиугольника в два раза больше его стороны.
Диагональ правильного шестиугольника равна диаметру описанной вокруг него окружности.
Диагональ правильного шестиугольника равна диаметру вписанной в него окружности, поделенному на косинус угла 30 градусов.
Ксения Репина
Ученик
(172)
11 лет назад
Диагональ любого многоугольника – это отрезок, соединяющий две не соседние вершины!
В шестиугольнике они могут быть разной длины, могут равняться радиусу описанной окружности, а могут быть и меньше.
Шестиугольник представляет собой геометрическую фигуру, многоугольник, который имеет шесть углов и
шесть сторон.
Также существует правильный шестиугольник. Он обладает следующим свойством: все ребра и углы равны.
Каждый угол составляет 120 градусов. А также он состоит из шести правильных и равных
треугольников.
- Длинная диагональ правильного шестиугольника через
площадь - Котроткая диагональ правильного шестиугольника через
площадь - Длинная диагональ правильного шестиугольника через
сторону - Короткая диагональ правильного шестиугольника через
сторону
Длинная диагональ через площадь
Длинной диагональю на рисунке являются отрезки ВЕ, AD и CF. Все диагонали будут равны между собой.
Это свойство касается как правильной фигуры, так и неправильной. Для нахождения длинной диагонали
правильного шестиугольника понадобится площадь полной фигуры (правильного шестиугольника), которую
можно найти по формуле S = (a * a * √3 * 6) / 4. А диагональ находится по
следующим образом:
D = √((S / 3√3) * 8)
где S — площадь правильного шестиугольника.
Цифр после
запятой:
Результат в:
Пример. Сторона шестиугольника равна 6 см. Тогда площадь: S = (6 * 6 * √3 * 6) / 4 = 54√3 см. D = √((54√3 / 3√3) * 8) = 12 см.
Короткая диагональ через площадь
Короткими диагоналями можно назвать BD, BF, AE или же DF. Для нахождения неизвестной стороны также,
как и в прошлой ситуации, понадобится площадь фигуры, которую возможно найти по следующей формуле:
S = (a * a * √3 * 6) / 4. После этого найденная величина подставляется в
готовую формулу:
D = √((S / √3) * 2)
где S — площадь правильного многоугольника.
Цифр после
запятой:
Результат в:
Пример. Как и в прошлой задаче, ребро равно 6 см. Тогда площадь правильного
шестиугольника = 54√3 см. Далее можно находить и искомую диагональ: D = √((54√3 / √3) * 2) = 6√3
Длинная диагональ через сторону
Длинной диагональю на рисунке являются отрезки ВЕ, AD и CF. Длинную диагональ правильно
шестиугольника можно вычислить и без нахождения площади. Для выполнения математических действий и
нахождения неизвестной переменной надо знать лишь ребро многоугольника:
D = 2a
где a — сторона правильного шестиугольника.
Цифр после
запятой:
Результат в:
Длинная диагональ состоит из двух сторон треугольников, прилегающих друг к другу, поэтому сторону
умножаем на 2.
Пример. В задаче дан правильный шестиугольник. Его ребро равно 3 см. Тогда длинная
диагональ равна 6 см.
Короткая диагональ через сторону
Также существует и другой способ нахождения короткой диагонали, равностороннего шестиугольника.
Например, диагонали BD. Для нахождения достаточно лишь знание стороны фигуры:
D = √(3 * a * a)
где a — сторона правильного шестиугольника.
Цифр после
запятой:
Результат в:
Пример. Сторона АВ равна 10 см. Тогда BD = D = √(3 * 10 * 10) = 10√3 см = 17 см.
Для более простого понимания такой темы, как вычисление диагонали правильного шестиугольника, стоит
для начала увидеть, что данный многоугольник состоит из шести равносторонних и равных между собой
треугольников. (Неправильный шестиугольник условно можно разделить на шесть равнобедренных
треугольник). О – это центр правильного шестиугольника. Он делит диагонали на равные отрезки. Также
точка пересечения длинных диагоналей является центром вписанной и описанных окружностей. Все
диагонали также равны между собой и делят углы на две равные части, то есть выполняют функцию
биссектрисы, а также высоты или медианы, так как были проведены в равнобедренном треугольнике. Таким
образом будет легче находить какие-то неизвестные отрезки.
Однако существует и более сложный метод – через нахождение площади фигуры. Данную формулу запомнить
просто: S = (a * a * √3) / 4 – она необходима, чтобы вычислить площадь
равностороннего треугольника, где величина а является стороной. А вышеупомянутая фигура состоит из
шести таких геометрических фигур, поэтому конечная формула будет выглядеть так: S = (a * a * √3 * 6) / 4
Таким образом, шестиугольник является не такой уж и сложной фигурой, как кажется на первый взгляд.
Достаточно изучить элементарные свойства и запомнить их.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,658 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,962 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Как посчитать диагональ
В геометрии существует несколько видов диагоналей. Диагональю называется отрезок, который соединяет две не соседние (не принадлежащие одной стороне или одному ребру) вершины многоугольника или многогранника. Различают так же диагонали граней, рассматриваемых как многоугольники и пространственные диагонали, соединяющие вершины разных граней многогранника. Существуют фигуры, у которых все диагонали равны между собой. На плоскости это правильный пятиугольник и квадрат, в пространстве – правильный октаэдр.Зная длины сторон правильного многоугольника или длины рёбер правильного многогранника можно вычислить длину любой диагонали.

Инструкция
В любом правильном многоугольнике углы равны между собой и вычисляются по формуле
?? = (N – 2) * 180?/N, где ?? – любой из углов правильного многоугольника, N – число вершин.
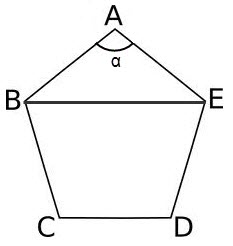
Зная углы при вершинах многоугольника, его диагонали можно вычислить, используя теорему косинусов
BE = v(AB? + AE? – 2 * AB * AE * cos??)
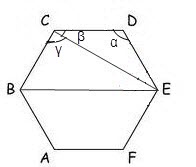
Если количество вершин больше пяти, то для вычисления диагоналей, которые соединяют вершины, лежащие на разных сторонах можно воспользоваться той же теоремой косинусов для вычисления углов образующихся треугольников. Например, в шестиугольнике ABCDEF, для нахождения диагонали BE, необходимо вычислить диагональ CE, затем по той же теореме косинусов вычислить угол ??, тогда ?? = ?? – ??. Таким образом,
BE = v(BC? + CE? – 2 * BC * CE * cos??).
Видео по теме
Обратите внимание
Для вычисления пространственной диагонали многогранника, необходимо построить сечение, содержащее эту диагональ, вычислить углы при вершинах этого сечения, рассматривая сечение как плоский многоугольник. Тогда диагональ можно рассчитать по приведённой выше схеме.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Шестиугольник – это шестигранный многоугольник. Правильный шестиугольник означает, что каждая сторона формы равна друг другу, в то время как неправильный шестиугольник имеет шесть неравных сторон. Форма имеет девять диагоналей, линии между внутренними углами. Хотя не существует стандартной формулы для нахождения диагоналей неправильных шестиугольников, для правильных шестиугольников девять диагоналей образуют шесть равносторонних треугольников, что позволяет легко определять длину каждой диагональной линии. Если известна одна сторона шестиугольника, то известны все стороны, и диагонали легко вычисляются.
Определите длину одной стороны шестиугольника. Для правильных шестиугольников все стороны равны: Таким образом, каждая сторона имеет одинаковую длину, и если одна сторона известна, то все равны. Известное или данное обозначено как «g» (заданная сторона).
Выпишите уравнение для нахождения диагонали правильного шестиугольника: d (диагональ) = 2g (заданная сторона).
Умножьте известную или заданную сторону шестиугольника на 2. Произведение – это длина диагонали правильного шестиугольника.
Хотя вы можете рассчитать количество диагоналей в неправильном шестиугольнике, для нахождения диагонального измерения неправильного потребуется сначала разбить шестиугольник на четыре треугольника. Однако, если они не являются правильными треугольниками, которые они вряд ли будут, нет формального для определения длины внутренней стороны, которая была бы диагональю. Теорема Пифагора применима только к прямоугольным треугольникам. если бы каждая сторона и угол были указаны вместе с площадью, то можно было бы определить диагонали, но это много переменных, которые можно принять.
