Как найти диагонали в равностороннем треугольнике

Свойства равностороннего треугольника: теория и пример задачи

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Свойства равностороннего треугольника

Свойство 1

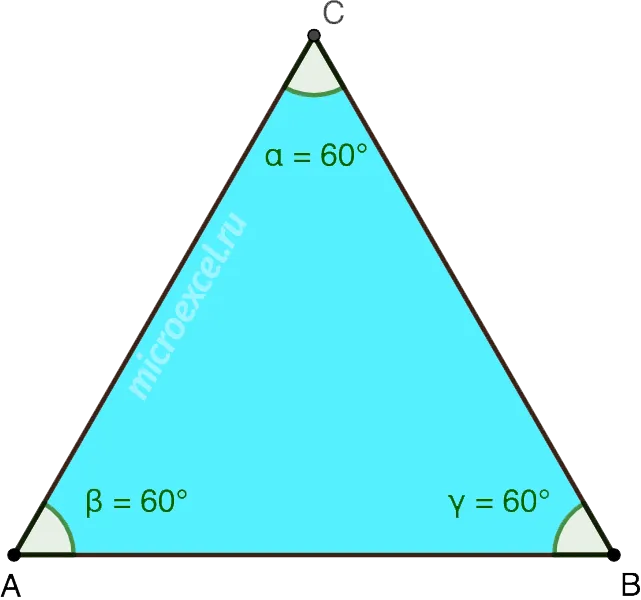
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

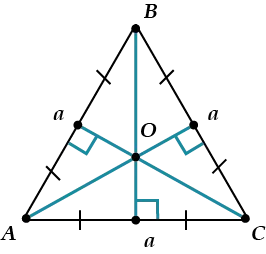
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

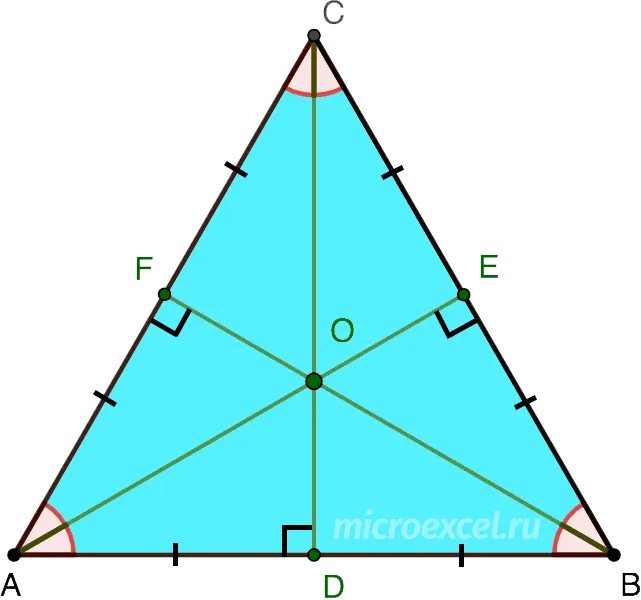
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

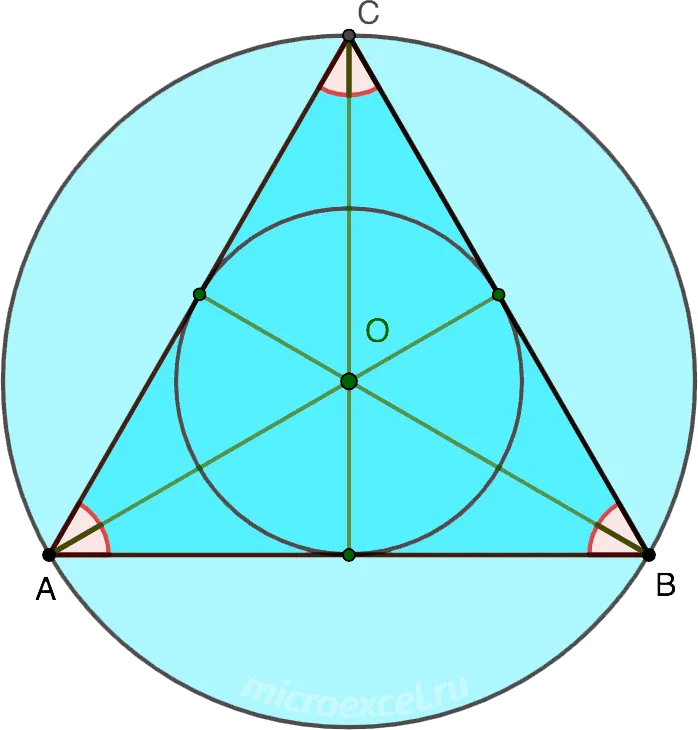
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

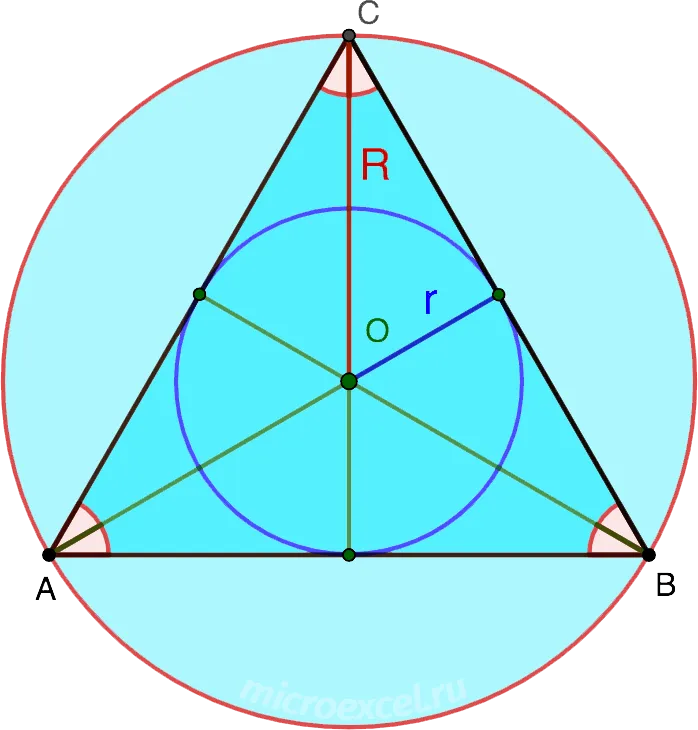
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Свойства равностороннего треугольника

Основные свойства равностороннего треугольника непосредственно следуют из свойств равнобедренного треугольника, частным случаем которого он является.

Свойства равностороннего треугольника

2) Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают:

AK — высота, медиана и биссектриса, проведённые к стороне BC;

BF — высота, медиана и биссектриса, проведённые к стороне AC;

CD — высота, медиана и биссектриса, проведённые к стороне AB.

Длины всех трёх высот (медиан, биссектрис) равны между собой:

Если a — сторона треугольника, то

3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).

4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин:

5) Расстояние от точки пересечения высот, биссектрис и медиан

до любой вершины треугольника равно радиусу описанной окружности:

6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности:

7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.

8) Радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной окружности:

Диагональ треугольника – формула

Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.

Треугольник

Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:

Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.

Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует

Рис. 1. Три медианы в треугольнике.

Прямоугольник

Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.

Диагональ прямоугольника или квадрата всегда:

• Делит фигуру на две равных прямоугольных треугольника.
• В полученных треугольниках диагональ будет являться гипотенузой
• Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора

Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.

При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.

Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.

Многоугольник

На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.

Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.

Рис. 2. Диагонали многоугольника.

В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.

Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.

Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.

Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.

Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:

$P=>$ – где n это число сторон многоугольника.

Проверим для квадрата:

Рис. 3. Диагонали квадрата.

Что мы узнали?

Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.

[spoiler title=”источники:”]

http://sprint-olympic.ru/uroki/matematika-uroki/15430-diagonal-treygolnika-formyla.html

[/spoiler]

Диагонали в равностороннем треугольнике

Freeman

Мастер

(1443),
закрыт

15 лет назад

Что они там делают ?
Вылетело что-то из головы …
Вроде как точкой пересечения они делятся в соотношении 1:2
Не так ли?

Тупоугольный треугольник содержит тупой угол. То есть угол более 90 градусов. Два других угла в таком треугольнике острые.

Равносторонний треугольник, свойства, признаки и формулы

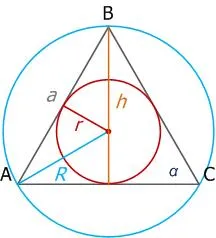
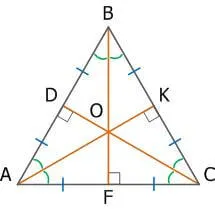
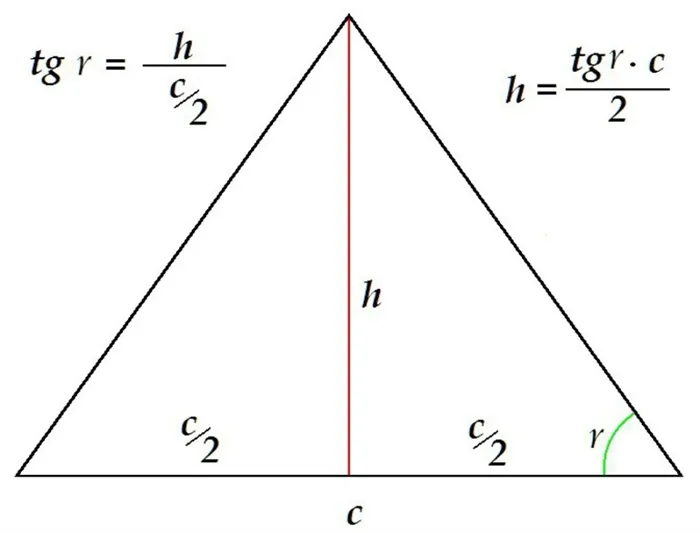
Равносторонний треугольник — это треугольник, у которого все стороны одинаковой длины и все углы одинаковой величины (60°).

Равносторонний треугольник (понятие, определение):

Равносторонний треугольник — это треугольник, у которого все стороны одинаковой длины и все углы одинаковой величины (60°).

Равносторонний треугольник также называют правильным или равносторонним треугольником.

По определению, каждый прямоугольный (равнобедренный) треугольник также является равнобедренным, но не каждый равнобедренный треугольник является прямоугольным (равносторонним). Другими словами, правильный треугольник — это частный случай равнобедренного треугольника.

Рисунок 1: Равнобедренный треугольник

AB = BC = AC — стороны треугольника, ∠ ABC = ∠ BAC = ∠ AC = 60° — углы треугольника.

Свойства равностороннего треугольника:

1. в равностороннем треугольнике все стороны имеют одинаковую длину.

2. в равностороннем треугольнике углы равны и составляют 60°.

3. в равностороннем треугольнике каждая диагональ, проведенная к каждой стороне, является биссектрисой угла, а высота и равны друг другу.

В равностороннем треугольнике биссектриса угла, проведенная к каждой стороне, является средней линией, а высота и равны друг другу.

В равностороннем треугольнике высота, проведенная на каждой стороне, является биссектрисой угла, а средняя линия и равны друг другу.

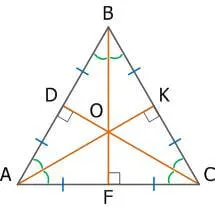
Рисунок 2. равнобедренный треугольник

4. в равностороннем треугольнике высоты, биссектрисы углов, медианы и медианы пересекаются в точке, называемой центром равностороннего треугольника. Он также является центром эндоцикла и перицикла.

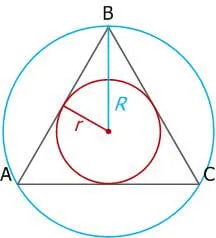
Рисунок 3. равнобедренный треугольник

R — радиус окружности, r — радиус эндо окружности.

5. радиус окружности равнобедренного треугольника в два раза больше радиуса эндокруга.

6. пересечение высот, биссектрис и медиан правильного треугольника делит каждую из них в соотношении 2:1, измеренном от вершин.

Рисунок 4. равнобедренный треугольник

AO : OK = BO : OA = CO : OD = 2 : 1

Определение равностороннего треугольника

Равносторонний (или прямоугольный) треугольник — это треугольник, у которого все стороны равны по длине. То есть, AB = BC = AC .

Примечание: Правильный многоугольник — это выпуклый многоугольник с равными сторонами и углами между ними.

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. То есть, a = b = c = 60° .

Свойство 2

Высота равностороннего треугольника равна биссектрисе угла, из которого он образован, среднему и центру.

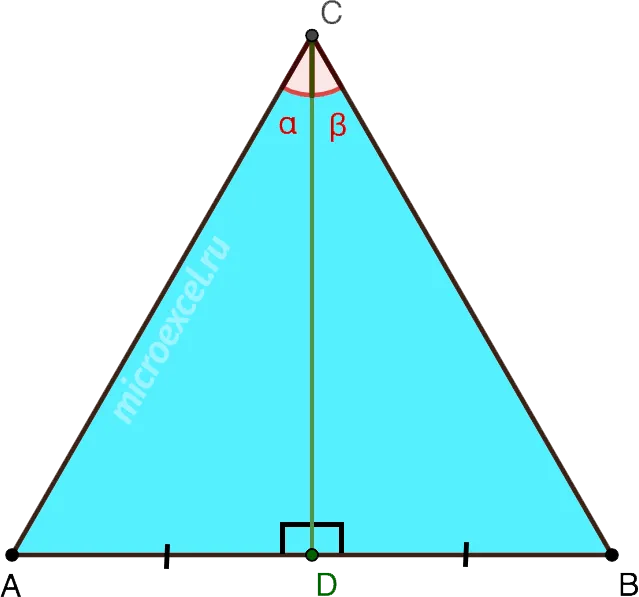
CD — медиана, высота и среднее значение AB и биссектриса угла ACB.

• CD перпендикулярна AB =>∠ADC = ∠BDC = 90°
• AD = DB
• ∠ACD = ∠DCB = 30°

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и средние значения всех сторон пересекаются в одной точке.

Свойство 4

Центры акроокружности и окружности совпадают и пересекаются на пересечении медиан, высот, биссектрис углов и центров.

Свойство 5

Решение Примените формулы, приведенные выше, чтобы найти неизвестные величины:

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r .

Свойство 6

Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и перпендикуляров совпадают — это одна и та же точка. Эта точка называется центром треугольника.

Почему? Рассмотрим равносторонний треугольник.

Он равнобедренный независимо от того, какая сторона взята за основание — он равнобедренный со всех сторон, так сказать.

Таким образом, каждая высота в равностороннем треугольнике также является биссектрисой угла, медианой и средним перпендикуляром!

В равностороннем треугольнике не (12) отдельных линий, как в обычном треугольнике, а только три!

Центр равностороннего треугольника — это центр конечной окружности и перикруга, а также пересечение высот и медиан.

Пример задачи

Свойство 3. В равностороннем треугольнике радиус перикруга в два раза больше радиуса конечного круга. (R=2cdot r)

Теперь должно быть понятно, почему это так.

Публикации по теме:

• Нахождение площади квадрата: формула и примеры
• Нахождение площади прямоугольника: формула и пример
• Нахождение площади треугольника: формула и примеры
• Нахождение площади круга: формула и примеры
• Нахождение площади ромба: формула и примеры
• Нахождение площади трапеции: формула и примеры
• Нахождение площади параллелограмма: формула и примеры
• Нахождение площади эллипса: формула и пример
• Нахождение площади выпуклого четырехугольника: формула и пример
• Нахождение периметра квадрата: формула и задачи
• Нахождение периметра прямоугольника: формула и задачи
• Нахождение периметра ромба: формула и задачи
• Нахождение периметра трапеции: формула и задачи
• Нахождение периметра параллелограмма: формула и задачи
• Нахождение длины окружности: формула и задачи
• Теорема Пифагора для прямоугольного треугольника: формула и задачи
• Теорема косинусов для треугольника: формула и задачи
• Теорема о сумме углов треугольника: формула и задачи
• Тригонометрические функции острого угла в прямоугольном треугольнике
• Нахождение объема конуса: формула и задачи
• Нахождение объема куба: формула и задачи
• Нахождение объема шара: формула и задачи
• Нахождение объема пирамиды: формула и задачи
• Нахождение площади правильного шестиугольника: формула и примеры
• Нахождение объема тетраэдра: формула и задачи
• Нахождение объема призмы: формула и задачи
• Нахождение площади поверхности куба: формула и задачи
• Нахождение площади поверхности цилиндра: формула и задачи
• Нахождение площади поверхности конуса: формула и задачи
• Нахождение площади поверхности шара (сферы): формула и задачи
• Нахождение площади поверхности вписанного в цилиндр шара
• Нахождение радиуса шара: формула и примеры
• Нахождение радиуса круга: формула и примеры
• Нахождение радиуса цилиндра: формула и примеры
• Нахождение площади правильной призмы: формула и задачи
• Нахождение площади правильной пирамиды: формулы
• Формула Герона для треугольника
• Теорема Менелая: формулировка и пример с решением
• Теорема о внешнем угле треугольника: формулировка и задачи
• Теорема Чевы: формулировка и пример с решением
• Теорема Стюарта: формулировка и пример с решением
• Теорема о трех перпендикулярах
• Теорема Фалеса: формулировка и пример решения задачи
• Геометрическая фигура: треугольник
• Признаки равенства треугольников
• Признаки подобия треугольников
• Признаки равенства прямоугольных треугольников
• Свойства равнобедренного треугольника: теория и задача
• Определение и свойства медианы треугольника
• Определение и свойства медианы прямоугольного треугольника

Свойства равностороннего треугольника

Свойство 1. В равностороннем треугольнике все углы равны между собой и равны (^>)

Естественно, не правда ли? Три одинаковых угла, в сумме (^>), значит, каждый по (^>)

Рассмотрим рисунок: Точка(O) является центром треугольника.

Таким образом, (OB) — это радиус окружности (обозначается (R)), а (OK) — радиус эндоцикла (обозначается (r)).

Но точка (O) также является пересечением пространств! Напомним, что медианы делятся пересечением в соотношении (2:1), считая от вершины.

Поэтому (OB=2cdot OK), т.е. (R=2cdot r).

Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются длиной стороны.

Давайте убедимся в этом.

Это уже должно быть понятно:

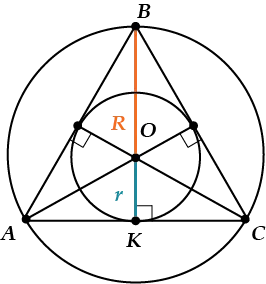
Мы постоянно работаем над улучшением этого учебника, и вы можете помочь нам. Доступ и неограниченное использование учебника Юклава (более 100 статей по всем темам ЕГЭ и ОГЭ, более 2000 решенных задач, более 20 вебинаров — практических занятий).

Радиус вписанной окружности равностороннего треугольника

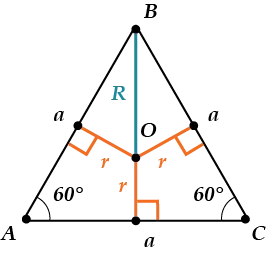
Открыть ответы…

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

• CD перпендикулярна AB => ∠ADC = ∠BDC = 90°
• AD = DB
• ∠ACD = ∠DCB = 30°

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Основные свойства равностороннего треугольника непосредственно следуют из свойств равнобедренного треугольника, частным случаем которого он является.

Свойства равностороннего треугольника

1) Все углы равностороннего треугольника равны по 60º.

2) Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают:

AK — высота, медиана и биссектриса, проведённые к стороне BC;

BF — высота, медиана и биссектриса, проведённые к стороне AC;

CD — высота, медиана и биссектриса, проведённые к стороне AB.

Длины всех трёх высот (медиан, биссектрис) равны между собой:

AK=BF=CD.

Если a — сторона треугольника, то

   

3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).

4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин:

AO:OK=BO:OF=CO:OD=2:1.

5) Расстояние от точки пересечения высот, биссектрис и медиан

до любой вершины треугольника равно радиусу описанной окружности:

BO=R,

   

или

   

6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности:

OF=r,

   

или

   

7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.

8) Радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной окружности:

R=2r.

9) Площадь равностороннего треугольника равна

   

периметр —