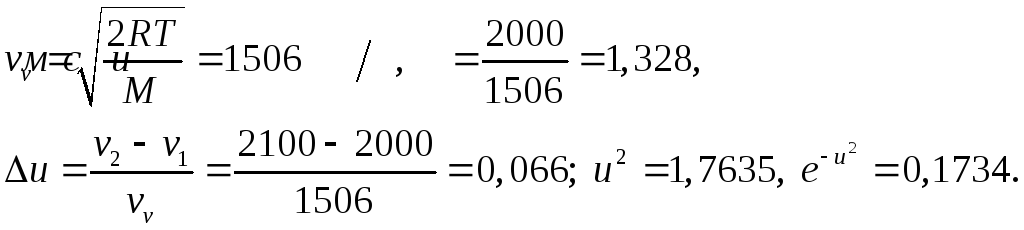Как найти диаметр атома ртути

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Хмм, ну допустим, что Ваша молекула — это шар. Шар — имеет объём и массу, а если мы найдём их отношение, то найдём и плотность нашей молекулы ртути.

1. m = ρ*V, где m — это масса молекулы, V — объём молекулы, ρ — плотность молекулы ртути, равная 13540 кг/м³(табличное значение).
2. Чтобы найти массу молекулы ртути, нам нужно взять из таблицы Менделеева молярную массу ртути и разделить на число Авогадро. 
m = M(Hg) / Nₐ = 200,59/6.02*10^23 = 33,32*10⁻²³ грамм = 33,32*10⁻²⁶ кг
3.Объём шара =  . Cледовательно:

V = m/ρ = 
Отсюда выражаем наш диаметр d:

 
Получилось красивое число:
d = 0,36 * 10⁻⁹ м = 0,36 нм (нано метров)
Ответ:
d = 0,36 нм 

Рассматривая
молекулы жидкости как шарики,
соприкасающиеся друг с другом, оценить
порядок величины диаметра молекулы:
1)воды;

2)
углерода. При тех же предположениях
оценить порядок величины диаметра
атома ртути и его объём. Плотности
жидкостей считать известными.

Решение.

Запишем
объём,приходящийся на одну молекулу.

V₁
= V_M/N_A,
(1)

где
V_M
– молярный объём, который найдём из
cоотношения

, (2)

где
M – молярная масса,  
– плотность вещества.

Так
как молекулы условно приняты за шарики,
то

V₁
=  d³, (3)

Подставив
(2) и (3) в (1), получим ,

откуда
для диаметра молекулы имеем

. (4)

Подставив
для воды её молярную массу, получим
значение диаметра молекулы:
.

Аналогичные
расчёты для молекул углерода и ртути
дают:

.

Видим,
что молекула ртути примерно в два раза
больше молекулы воды. Найдём объём
одной молекулы ртути:

.

Пример
7.

Какая
часть молекул водорода при 150 ^оС
обладает скоростями в интервале от
2000 м/с до 2100 м/с?

Решение.

Используем
закон распределения Максвелла,
записанный через безразмерную величину
u = v/v_v,
где v – скорость молекулы, v_v
–
наиболее вероятная скорость молекул:

.

Здесь
dN – число молекул со скоростями от v =
v_vu
до v + dv = v_vu
+ v_vdu;

N
– полное число молекул.

Вместо
значка d
может быть значок
.

Подсчитаем
отдельно v_v,u,du:

Подставив
полученные данные в исходную формулу,
найдём

N/N
= 0,0458.

Пример
8.

Найти
молярную и удельную теплоёмкости аргона
при постоянном объёме и постоянном
давлении. Молярная масса аргона M = 0,04
кг/моль. Принять R = 8,31 Дж/моль∙К. Газ
считать идеальным и одноатомным.

Решение.

В
соответствии с классической теорией
мольные изохорическая и изобарическая
теплоёмкости имеют следующие значения:

C_V

= (i/2)R = 12,46 Дж/(моль∙К);
C_p
= (i+2)R/2 = 20,78 Дж/(моль∙К).

Удельные
теплоёмкости соответственно будут

C_V
= C_V/M
= 311,5 Дж/(кг∙К), c_p
=
C_p/M
= 519,5 Дж/(кг∙К).

Пример
9.

Между
двумя пластинами, находящимися на
расстоянии 2 мм друг от друга, находится
воздух. Между пластинами поддерживается
разность температур  –.
Площадь каждой пластины

S
= 100 см².
Какое количество тепла передаётся за
счёт теплопроводности воздуха от одной
пластины к другой за время t = 10 мин ?
Считать, что воздух находится при
нормальных условиях. Диаметр молекул
воздуха принять
.
Молярная масса воздуха 0,029 кг/моль.

Решение.

Согласно
закону Фурье количество тепла ,
переносимое через поверхность S за
время ,
определится по формуле

, (1)

где

– коэффициент теплопроводности; c_V
–
изохорическая удельная теплоёмкость;
 –
плотность;

– средняя длина свободного пробега
молекулы; v – средняя скорость их
движения.

Из
уравнения состояния следует

.

Согласно
молекулярно-кинетическим соображениям

 . (2)

Во
второй формуле (2) вместо концентрации
n
подставлено её выражение p/kT.
Подставляя формулы (2) в выражение (1),
получим

 .

Подставив
данные, получим.

Подставив
в формулу (1)
,
получим

.

2019-12-31   

Оцените размер атома ртути, если известны: $sigma$ – коэффициент поверхностного натяжения ртути (в единицах $frac{энергия}{площадь}$), $rho$ – плотность ртути, $r$ – удельная теплота парообразования ртути.

Решение:

При плотной упаковке молекул (что вполне справедливо для жидкостей) каждая молекула имеет 12 соседей. (Покажите это самостоятельно. Подсказка: рассмотрите телесные углы, в которых видны из центра молекулы ее соседи.) Из этих 12 молекул 6 окружают ее кольцом, а еще по три молекулы находятся с каждой стороны от плоскости кольца. Когда мы создаем плоскую свободную поверхность, мы отрываем от молекулы по 3 молекулы из 12, то есть разрываем четверть всех связей.

Итак, создавая свободную поверхность площади $S$, мы совершаем работу

$A = sigma S = frac{1}{4} rm = frac{1}{4} rV rho = frac{1}{4} rSd rho$,

где $d$ – диаметр молекулы (“высота” одного слоя). Отсюда

$d = frac{4 sigma}{r rho}$.

Для ртути $sigma = 0,47 Дж/м^{2}, rho = 13,6 cdot 10^{3} кг/м^{3}, r = 2,82 cdot 10^{5} Дж/кг$, и $d approx 10^{-10} м$.

Оценим диаметр молекулы стандартным способом – по объему, занимаемому 1 молем: на 1 молекулу приходится объем

$v = frac{ mu }{ rho N_{A} } = frac{1}{6} pi d^{3}$,

откуда

$d = left ( frac{6 mu }{ pi rho N_{A} } right )^{1/3}$

Для ртути $mu = 0,2 кг/моль$, и $d = 3,6 cdot 10^{-10} м$, то есть наша оценка по энергии связей вполне разумна.

Подумайте, годится ли такой способ оценки (по энергии связей) для многоатомных молекул.