Как найти диаметр атома водорода - Сайт, где вы сможете решить свои вопросы

Каков диаметр атома водорода и каков диаметр протона в атоме водорода?

Домашние задания

Викуля Петрова

9 ноября 2020 · 2,0 K

ОтветитьУточнить

Аква Композит64

Психология отношений, психология личности. Производство химии: антискалантов, пылеподавите… · 10 нояб 2020 · akva-kompozit.ru

ОтвечаетVictor Matsura

Диаметр атома водорода 0,529*10−10 м, – это радиус электронной оболочки, боровский радиус. А диаметр протона – 2,5*10−13 см.

Но надо иметь ввиду, что эти радиусы весьма условны, так как у электрона есть разные орбитали (поэтому радиус атома может быть больше), а протон вообще как бы рыхлый – он состоит из более плотного ядра и менее плотных оболочек.

1,9 K

Комментировать ответ…Комментировать…

Вы знаете ответ на этот вопрос?

Поделитесь своим опытом и знаниями

Войти и ответить на вопрос

Источник

Для работы проектов iXBT.com нужны файлы cookie и сервисы аналитики.
Продолжая посещать сайты проектов вы соглашаетесь с нашей
Политикой в отношении файлов cookie

Тема наглядной визуализации мне кажется довольно интересной и сегодня поговорим о визуализации микромира (возможности представления и осознания бесконечно малых размеров на основе привычных объектов) на примере атома водорода, но в масштабе, который можно легко себе представить и осознать.

Источник иллюстрации – pixabay.com

В школьном курсе физики, строение атомов представлено в соответствии с планетарной моделью Резерфорда. В центре атома расположено ядро, имеющее положительный заряд. Вокруг ядра по орбитам движутся электроны, которые имеют отрицательный заряд. А “суммарно” сам атом нейтрален. Водород же имеет всего один электрон, который по орбите движется вокруг ядра.

Схема атома водорода

Фото атома водорода. Источник иллюстрации – ru.pinterest.com

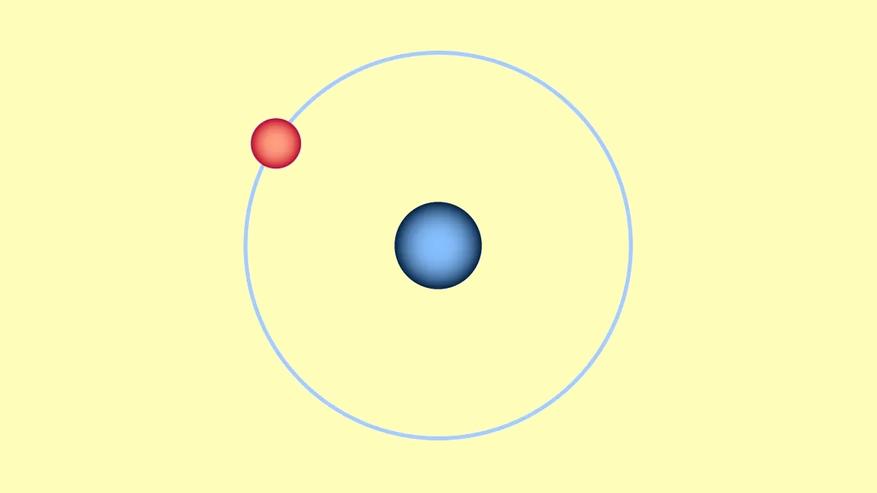
Понятно, что измерить радиус атома, а тем более ядра и электрона невозможно ни с помощью сильнейшего микроскопа, ни тем более линейкой. Поэтому ученые пытаются измерить данные величины “косвенными” методами. С развитием науки, техники и технологий официальные данные “замеров” величин микромира доказываются, меняются, уточняются. Давайте для нашей визуализации возьмем принятые (понятно, что с большим допуском) в “научно-популярном” мире размера атома и его “составных частей”.

Давайте увеличим радиус атома до размеров футбольного поля, т.е. до 100 метров (стандартный размер футбольного поля от 100 до 120 метров. Возьмем самое “короткое”). Увеличив во столько же раз размеры ядра и электрона получим в наших пропорциях радиус ядра – 1 см, а радиус электрона – 0,1 см. Диаметры же ядра и электрона будут 2 см и 0,2 см соответственно. Под эти размеры как нельзя лучше подпадают черешня и головка спички – их и возьмем для визуализации.

Получаем такую “картинку”. За одними воротами расположим черешню (это ядро), за другими спичечную головку (это электрон). Длина самого поля – это радиус атома.

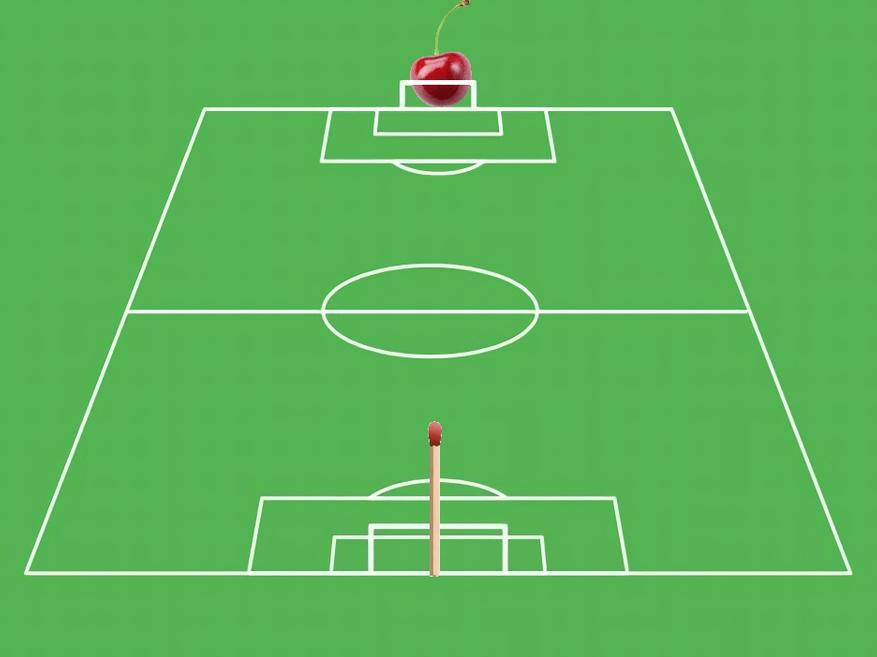
Пусть “официально признанные” в микромире размеры атома и его “составных частей” довольно приблизительны, но теперь, в другом масштабе, стали понятны относительные размеры атома водорода, ядра, электрона и расстояния между ядром и электроном в атоме.

Если тема статьи Вам показалась интересной, то можете ознакомиться со статьей о “визуализации”, но уже макромира – “Наглядная визуализация для осознания больших величин на примере Солнца, Земли и скорости света”.

Сейчас на главной

Новости

Публикации

Десять лет назад на выставке CES 2013 объявился аппарат Huawei Ascend Mate — первый в мире смартфон с диагональю экрана больше 6 дюймов. До этого подобные гаджеты если и выпускались, то…

После путешествия по Ирану меня живо интересует тема голубиных башен. В Египте они тоже есть. Я попыталась найти такие сооружения в Хургаде. И нашла! На примете было три локации. Первая…

Компания
Eltronic в 2023 году обновила модель ELTRONIC 20-33 DANCE BOX 1000. Музыкальная
колонка похудела и у нее появилась талия. Ну по крайней мере так можно
охарактеризовать новообретенные…

Некоторые хозяева кошек уверены, что их любимцы
понимают практически все, только не могут говорить. Ведь «мурлыки»
часто мяукают в ответ, когда
с ними разговариваешь. Это выглядит так,…

В ряду забавной фонарной мелочи от Wurkkos пополнение. WK04 может работать как обычный карманный фонарик, освещая путь под ногами. А еще у него есть встроенный рассеиватель, с которым фонарик…

Бетон — это одно из самых древних и популярных строительных материалов, известный ещё с Древнего Рима. Понятно, что сейчас рецептура немного изменилась и используются более качественные…

Источник

А́том водоро́да — физико-химическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра, как правило, входит протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон образует электронную оболочку; наибольшая вероятность обнаружения электрона в единичном объёме наблюдается для центра атома. Интегрирование по сферическому слою показывает, что наибольшая вероятность обнаружения электрона в единичном слое соответствует среднему радиусу, равному боровскому радиусу ${displaystyle a_{0}=0{,}529}$ ангстрема.

Атом водорода имеет особое значение в квантовой механике и релятивистской квантовой механике, поскольку для него задача двух тел имеет точное или приближённое аналитическое решение. Эти решения применимы для разных изотопов водорода (с соответствующими поправками).

В квантовой механике атом водорода описывается двухчастичной матрицей плотности или двухчастичной волновой функцией. Также упрощённо рассматривается как электрон в электростатическом поле бесконечно тяжёлого атомного ядра, не участвующего в движении (или просто в кулоновском электростатическом потенциале вида 1/r). В этом случае атом водорода описывается редуцированной одночастичной матрицей плотности или волновой функцией.

В 1913 году Нильс Бор предложил модель атома водорода, имеющую множество предположений и упрощений, и вывел из неё спектр излучения водорода. Предположения модели не были полностью правильны, но тем не менее приводили к верным значениям энергетических уровней атома.

Результаты расчётов Бора были подтверждены в 1925—1926 годах строгим квантовомеханическим анализом, основанном на уравнении Шрёдингера. Решение уравнения Шрёдингера для электрона в электростатическом поле атомного ядра выводится в аналитической форме. Оно описывает не только уровни энергии электрона и спектр излучения, но и форму атомных орбиталей.

Решение уравнения Шрёдингера[править | править код]

Решение уравнения Шрёдингера для водородного атома использует тот факт, что кулоновский потенциал является изотропным, то есть не зависит от направления в пространстве, другими словами, обладает сферической симметрией. Хотя конечные волновые функции (орбитали) не обязательно сферически симметричны, их зависимость от угловой координаты следует полностью из изотропии основного потенциала: собственные значения оператора Гамильтона можно выбрать в виде собственных состояний оператора углового момента. Это соответствует тому факту, что угловой момент сохраняется при орбитальном движении электрона вокруг ядра. Отсюда следует, что собственные состояния гамильтониана задаются двумя квантовыми числами углового момента l и m (целые числа). Квантовое число углового момента l может принимать значения 0, 1, 2… и определяет величину углового момента. Магнитное квантовое число может принимать m = −l, …, +l; оно определяет проекцию углового момента на (произвольно выбранную) ось z.

В дополнение к математическим выражениям для волновых функций полного углового момента и проекции углового момента нужно найти выражение для радиальной зависимости волновой функции. В потенциале 1/r радиальные волновые функции записываются с использованием полиномов Лагерра. Это приводит к третьему квантовому числу, которое называется основным квантовым числом n и может принимать значения 1, 2, 3… Основное квантовое число в атоме водорода связано с полной энергией атома. Заметим, что максимальное значение квантового числа углового момента ограничено основным квантовым числом: оно может изменяться только до n − 1, то есть l = 0, 1, …, n−1.

Из-за сохранения углового момента состояния с одинаковыми l, но различными m в отсутствие магнитного поля имеют одну и ту же энергию (это выполняется для всех задач с аксиальной симметрией). Кроме того, для водородного атома состояния с одинаковыми n, но разными l также вырождены (то есть имеют одинаковую энергию). Однако это свойство — особенность лишь атома водорода (и водородоподобных атомов), оно не выполняется для более сложных атомов, которые имеют (эффективный) потенциал, отличающийся от кулоновского (из-за присутствия внутренних электронов, экранирующих потенциал ядра).

Если мы примем во внимание спин электрона, то появится последнее, четвёртое квантовое число, определяющее состояния атома водорода — проекция углового момента собственного вращения электрона на ось Z. Эта проекция может принимать два значения. Любое собственное состояние электрона в водородном атоме полностью описывается четырьмя квантовыми числами. Согласно обычным правилам квантовой механики, фактическое состояние электрона может быть любой суперпозицией этих состояний. Это объясняет также, почему выбор оси Z для квантования направления вектора углового момента является несущественным: орбиталь для данных l и $m^{prime },$ полученных для другой выделенной оси $Z^{prime },$ всегда представляется как подходящая суперпозиция различных состояний с разными m (но тем же самым l), которые были получены для Z.

Рассмотрим сейчас решение уравнения Шрёдингера для атома водорода. Так как потенциальная функция электрона в атоме водорода имеет вид $U(r)=-{tfrac {e^{2}}{r}},$ где e — заряд электрона (и протона), r — радиус-вектор, то уравнение Шрёдингера запишется следующим образом:

$Delta psi +{frac {2m}{hbar ^{2}}}left(E+{frac {e^{2}}{r}}right)psi =0.$

Здесь ψ — волновая функция электрона в системе отсчёта протона, m — масса электрона, — постоянная Планка, E — полная энергия электрона, $Delta ={frac {partial ^{2}}{partial x^{2}}}+{frac {partial ^{2}}{partial y^{2}}}+{frac {partial ^{2}}{partial z^{2}}}$ — оператор Лапласа.
Так как потенциальная функция зависит от r, а не от координат по отдельности, удобно будет записать лапласиан в сферической системе координат В ней он выглядит следующим образом:

$Delta psi ={frac {1}{r^{2}}}{frac {partial }{partial r}}left(r^{2}{frac {partial psi }{partial r}}right)+{frac {1}{r^{2}sin ^{2}theta }}{frac {partial ^{2}psi }{partial varphi ^{2}}}+{frac {1}{r^{2}sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial psi }{partial theta }}right).$

Уравнение Шрёдингера в сферических координатах:

${frac {1}{r^{2}}}{frac {partial }{partial r}}left(r^{2}{frac {partial psi }{partial r}}right)+{frac {1}{r^{2}sin ^{2}theta }}{frac {partial ^{2}psi }{partial varphi ^{2}}}+{frac {1}{r^{2}sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial psi }{partial theta }}right)+{frac {2m}{hbar ^{2}}}left(E+{frac {e^{2}}{r}}right)psi =0.$

В этом уравнении psi — функция трёх переменных Разделим его на три более простых уравнения. Для этого представим функцию как произведение трёх функций: Эти функции будем обозначать просто Тогда:

${{frac {{partial }{psi }}{{partial }r}}}={{frac {{partial }R}{{partial }r}}}{Theta }{Phi },~~{{frac {{partial }{psi }}{{partial }{theta }}}}={{frac {{partial }{Theta }}{{partial }{theta }}}}R{Phi },~~{{frac {{partial }{psi }}{{partial }{varphi }}}}={{frac {{partial }{Phi }}{{partial }{varphi }}}}{Theta }R.$

После подстановки значений частных производных в уравнение Шрёдингера получим:

${{frac {1}{r^{2}}}}{{frac {partial }{{partial }r}}}left({r^{2}}{{frac {{partial }R}{{partial }r}}}right){Theta }{Phi }+{{frac {1}{{r^{2}}{sin ^{2}}{theta }}}}{{frac {{{partial }^{2}}{Phi }}{{partial }{{varphi }^{2}}}}{Theta }{R}}+{{frac {1}{{r^{2}}{sin }{theta }}}}{{frac {partial }{{partial }{theta }}}}left(sin theta {{frac {{partial }{Theta }}{{partial }{theta }}}}right){R}{Phi }+{{frac {2m}{hbar ^{2}}}}{left(E+{{frac {e^{2}}{r}}}right){R}{Theta }{Phi }}=0.$

Умножим уравнение на ${tfrac {r^{2}sin ^{2}theta }{RTheta Phi }}:$

${{frac {{sin ^{2}}{theta }}{R}}}{{frac {partial }{{partial }r}}}left({r^{2}}{{frac {{partial }R}{{partial }r}}}right)+{{frac {1}{Phi }}}{{frac {{{partial }^{2}}{Phi }}{{partial }{{varphi }^{2}}}}}+{{frac {sin theta }{Theta }}}{{frac {partial }{{partial }{theta }}}}left(sin theta {{frac {{partial }{Theta }}{{partial }{theta }}}}right)+{frac {2mr^{2}sin ^{2}theta }{hbar ^{2}}}left(E+{{frac {e^{2}}{r}}}right)=0.$

Второе слагаемое тут зависит только от φ. Перенесём его в правую часть равенства.

${frac {sin ^{2}theta }{R}}{frac {partial }{partial r}}left(r^{2}{frac {partial R}{partial r}}right)+{frac {sin theta }{Theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial Theta }{partial theta }}right)+{frac {2mr^{2}sin ^{2}theta }{hbar ^{2}}}left(E+{frac {e^{2}}{r}}right)=-{frac {1}{Phi }}{frac {partial ^{2}Phi }{partial varphi ^{2}}}.~~~(1)$

Равенство возможно, когда обе части равны какой-то постоянной величине. Обозначим её ${displaystyle m_{l}^{2}.}$ Следовательно:

${frac {partial ^{2}Phi }{partial varphi ^{2}}}=-m_{l}^{2}Phi .$

Решением этого уравнения являются функции:

$Phi =A~sin(m_{l}varphi ),~~Phi =Acos(m_{l}varphi ).$

Угол φ может изменяться от 0 до 2π. Функция Phi должна быть периодической с периодом 2π. Это возможно, только если $m_{l}=0,pm 1,pm 2,pm 3,dots$ Таким образом, из решения уравнения Шрёдингера получаем значение одного из квантовых чисел (конечно, из него можно получить их все). Число $m_{l}$ называется магнитным квантовым числом.

Далее, интегрируя квадрат модуля функции Phi от 0 до 2π и приравнивая полученное выражение к единице, получим, что $A={tfrac {1}{{sqrt {2pi }}}}.$

Далее рассмотрим левую часть уравнения (1). Она, конечно, равна $m_{l}^{2}:$

Разделим уравнение на $sin ^{2}theta :$

${frac {1}{R}}{frac {partial }{partial r}}left(r^{2}{frac {partial R}{partial r}}right)+{frac {1}{Theta sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial Theta }{partial theta }}right)+{frac {2mr^{2}}{hbar ^{2}}}left(E+{frac {e^{2}}{r}}right)={frac {m_{l}^{2}}{sin ^{2}theta }}.$

После аналогичного вышеуказанному перенесению второго слагаемого в правую часть и обозначения величины, которой равны эти части, через beta , получаем:

${frac {m_{l}^{2}}{sin ^{2}theta }}-{frac {1}{Theta sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial Theta }{partial theta }}right)=beta .$

${frac {1}{R}}{frac {partial }{partial r}}left(r^{2}{frac {partial R}{partial r}}right)+{frac {2mr^{2}}{hbar ^{2}}}left(E+{frac {e^{2}}{r}}right)=beta .$

Решение этих двух последних уравнений приводит к значениям l и n соответственно. Три квантовых числа в совокупности полностью описывают состояния электрона в атоме водорода.

Модуль полной энергии электрона в стационарном состоянии в атоме водорода обратно пропорционален $n^{2}.$ Число n называется главным квантовым числом. Оно может иметь значения от 1 до infty . Его связь с энергией см. ниже.

Число l называется азимутальным квантовым числом и определяет орбитальный момент количества движения электрона и форму электронного облака; может иметь значения от 0 до n − 1 (n здесь относится к энергетическом уровню, на котором находится рассматриваемый электрон).

Магнитное квантовое число $m_{l}$ определяет проекцию орбитального момента количества движения на выбранную ось в магнитном поле. Эта проекция равна $m_{l}hbar .$

Математическое описание атома водорода[править | править код]

Энергетический спектр[править | править код]

Энергетические уровни атома водорода, включая подуровни тонкой структуры, записываются в виде:

${displaystyle E_{nj}={frac {E_{0}}{n^{2}}}left(1+{frac {alpha ^{2}}{n^{2}}}left({frac {n}{j+{frac {1}{2}}}}-{frac {3}{4}}right)right),}$

где

— постоянная тонкой структуры,

— собственное значение оператора полного момента импульса.

Энергию $E_{0}$ можно найти в простой модели Бора, с массой электрона m_e и зарядом электрона e:

$E_{0}=-{frac {m_{e}e^{4}}{8h^{2}varepsilon _{0}^{2}}}$

(в системе СИ),

где h — постоянная Планка, $varepsilon _{0}~-$

электрическая постоянная. Величина E₀ (энергия связи атома водорода в основном состоянии) равна 13,62323824 эВ = 2,182700518⋅10⁻¹⁸ Дж. Эти значения несколько отличаются от действительного значения E₀, поскольку в расчёте не учтена конечная масса ядра и эффекты квантовой электродинамики.

Волновые функции[править | править код]

В сферических координатах волновые функции имеют вид:

${displaystyle psi _{nlm}(r,theta ,varphi )={sqrt {frac {(n-l-1)!}{2n{cdot }(n+l)!}}}{cdot }{left({frac {2}{na_{0}}}right)}^{frac {3}{2}}{cdot }exp {left({-{frac {r}{na_{0}}}}right)}{cdot }{left({frac {2r}{na_{0}}}right)}^{l}L_{n-l-1}^{2l+1}{left({frac {2r}{na_{0}}}right)}cdot Y_{l,m}(theta ,varphi ),}$

где: $a_{0}$

— Боровский радиус,

${displaystyle L_{n-l-1}^{2l+1}{left({frac {2r}{na_{0}}}right)}}$

— обобщённые полиномы Лагерра степени

от функции ${displaystyle {frac {2r}{na_{0}}},}$

${displaystyle Y_{l,m}(theta ,varphi )}$

— нормированные на единицу сферические функции.

Угловой момент[править | править код]

Собственные значения для оператора углового момента:

$L^{2}|n,l,mrangle ={hbar }^{2}l(l+1)|n,l,mrangle ,$

${displaystyle L_{z}|n,l,mrangle =hbar m|n,l,mrangle .}$

Нахождение энергии электрона из модели Бора[править | править код]

Вычислим уровни энергии атома водорода без учёта тонкой структуры, используя простую модель атома Бора. Для этой цели можно сделать грубое допущение электрона, двигающегося по круговой орбите на фиксированном расстоянии. Приравнивая кулоновскую силу притяжения ${displaystyle {frac {e^{2}}{4pi varepsilon _{0}r_{n}^{2}}}}$ центростремительной силе ${displaystyle {frac {m_{e}v^{2}}{r}},}$ получим:

${displaystyle {frac {e^{2}}{4pi varepsilon _{0}r_{n}}}=m_{e}v_{n}^{2}.}$

Здесь ${displaystyle m_{e}~-}$ масса электрона, ${displaystyle v_{n}~-}$ его скорость на орбите радиуса ${displaystyle r_{n},}$ $varepsilon _{0}~-$ диэлектрическая проницаемость вакуума (электрическая постоянная).

Отсюда кинетическая энергия электрона:

${displaystyle {frac {m_{e}v_{n}^{2}}{2}}={frac {e^{2}}{8pi varepsilon _{0}r}},}$

где

расстояние от электрона до ядра.

Потенциальная его энергия:

${displaystyle E_{pot}=-{frac {e^{2}}{4pi varepsilon _{0}r}}.}$

Полная энергия, соответственно, равна:

${displaystyle E=-{frac {e^{2}}{8pi varepsilon _{0}r}}.}$

Для нахождения радиуса r_n стационарной орбиты с номером n рассмотрим систему уравнений, в которой второе уравнение есть математическое выражение первого постулата Бора ${displaystyle m_{e}v_{n}r_{n}={frac {nh}{2pi }}:}$

${displaystyle {frac {m_{e}v_{n}^{2}}{r_{n}}}={frac {e^{2}}{4pi varepsilon _{0}r_{n}^{2}}},}$

${displaystyle m_{e}v_{n}r_{n}={frac {nh}{2pi }}}$

Отсюда получаем выражение для радиуса стационарной орбиты с номером n:

${displaystyle r_{n}={frac {varepsilon _{0}n^{2}h^{2}}{pi m_{e}e^{2}}}.}$

Радиус первой орбиты оказывается равным ${displaystyle r_{1}=a_{0}~approx ~5,291769241times 10^{-11}}$ метра. Эта константа называется боровским радиусом.

Подставляя это значение в выражение для энергии, получим:

${displaystyle E_{n}=-{frac {1}{n^{2}}}{frac {m_{e}e^{4}}{8h^{2}varepsilon _{0}^{2}}}.}$

Отсюда мы можем найти волновое число (по определению это обратная длина волны или число длин волн, укладывающихся на 1 см) фотона, излучаемого атомом водорода за один переход из возбуждённого состояния с главным квантовым числом $n_{1}$ в состояние с неким фиксированным главным квантовым числом ${displaystyle n_{2}:}$

${displaystyle upsilon =R_{H}left({frac {1}{n_{2}^{2}}}-{frac {1}{n_{1}^{2}}}right),}$

где $R=me^{4}/4pi chbar ^{3}$

постоянная Ридберга в системе СГС (она равна 109 737,31568539 см⁻¹)^[1].

Визуализация орбиталей атома водорода[править | править код]

Плотность вероятности для электрона при различных квантовых числах (l)

Изображение справа показывает первые несколько орбиталей атома водорода (собственные функции гамильтониана). Они представляют собой поперечные сечения плотности вероятности, величина которой отражена цветом (чёрный цвет соответствует минимальной плотности вероятности а белый — максимальной). Квантовое число углового момента l обозначено в каждой колонке, используя обычные спектроскопические обозначения (s означает l = 0; p: l = 1; d: l = 2). Главное квантовое число n (= 1, 2, 3…) отмечено справа от каждого ряда. Для всех картин магнитное квантовое число m равно 0, и сечение взято в плоскости — XZ, Z — вертикальная ось. Плотность вероятности в трёхмерном пространстве получается при вращении картинки вокруг оси Z.

Основное состояние, то есть состояние самой низкой энергии, в котором обычно находится электрон, является первым, состоянием 1s (n = 1, l = 0). Изображение с большим количеством орбиталей доступно до более высоких чисел n и l. Отметим наличие чёрных линий, которые появляются на каждой картинке, за исключением первой. Они — узловые линии (которые являются фактически узловыми поверхностями в трёх измерениях). Их общее количество всегда равно n − 1, которое является суммой числа радиальных узлов (равного n − l − 1) и числа угловых узлов (равного l).

Строение и свойства атома водорода[править | править код]

Образование атома водорода и его спектр излучения[править | править код]

Схема энергетических уровней атома водорода и спектральные серии

При попадании в электрическое поле положительно заряженного протона и отрицательно заряженного электрона происходит захват последнего протоном — образуется атом водорода. Образовавшийся атом водорода находится в возбуждённом состоянии. Время жизни атома водорода в возбуждённом состоянии — доли или единицы наносекунд (10⁻⁸—10⁻¹⁰сек)^[2], однако очень высоковозбуждённые атомы, находящиеся в состоянии с большими главными квантовыми числами при отсутствии столкновений с другими частицами, в очень разрежённых газах могут существовать до нескольких секунд. Снятие возбуждения атома происходит за счёт излучения фотонов с фиксированной энергией, проявляющихся в характерном спектре излучения водорода. Поскольку объём газообразного атомарного водорода содержит множество атомов в различных состояниях возбуждения, спектр состоит из большого числа линий.

Схема образования спектра атомарного водорода и спектральные серии представлена на рисунке^[3].

Линии спектра серии Лаймана обусловлены переходом электронов на нижний уровень с квантовым числом n = 1 с уровней с квантовыми числами n = 2, 3, 4, 5, 6… Линии Лаймана лежат в ультрафиолетовой области спектра. Линии спектра серии Бальмера обусловлены переходом электронов на уровень с квантовым числом n = 2 с уровней с квантовыми числами n = 3, 4, 5, 6… и лежат в видимой области спектра.

Линии спектра серий Пашена, Брэкета и Пфунда обусловлены переходом электронов на уровни с квантовыми числами n, равными 3, 4 и 5 (соответственно), и расположены в инфракрасной области спектра^[4].

В нормальном (основном) состоянии (главное квантовое число n = 1) атом водорода в изолированном виде может существовать неограниченное время. Согласно квантовохимическим расчётам, радиус места наибольшей вероятности нахождения электрона в атоме водорода в нормальном состоянии (главное квантовое число n = 1) равен 0,529 Å. Этот радиус является одной из основных атомных констант, он получил название боровский радиус (см. выше). При возбуждении атома водорода электрон проходит на более высокий квантовый уровень (главное квантовое число n = 2, 3, 4 и т. д.), при этом радиус места наибольшей вероятности нахождения электрона в атоме возрастает пропорционально квадрату главного квантового числа:

r_n = a₀ · n².

Возбуждение и ионизация атома водорода[править | править код]

Возбуждение атома водорода происходит при нагревании, электроразряде, поглощении света и т. д., причём в любом случае атом водорода поглощает определённые порции — кванты энергии, соответствующие разности энергетических уровней электронов. Обратный переход электрона сопровождается выделением точно такой же порции энергии. Квантовые переходы электрона соответствуют скачкообразному изменению концентрического шарового слоя вокруг ядра атома водорода, в котором преимущественно находится электрон (шаровым слой является только при нулевом значении азимутального квантового числа l).

Согласно квантовомеханическим расчётам, наиболее вероятное расстояние электрона от ядра в атоме водорода равно боровскому радиусу ~ 0,53 Å при n = 1; 2,12 Å — при n = 2; 4,77 Å — при n = 3 и так далее. Значения этих радиусов относятся как квадраты натуральных чисел (главного квантового числа) 1² : 2² : 3²…. В очень разреженных средах (например, в межзвёздной среде) наблюдаются атомы водорода с главными квантовыми числами до 1000 (ридберговские атомы), чьи радиусы достигают сотых долей миллиметра.

Если электрону в основном состоянии придать дополнительную энергию, превышающую энергию связи E₀ ≈ 13,6 эВ, происходит ионизация атома водорода — распад атома на протон и электрон.

Радиальное распределение вероятности нахождения электрона в атоме.

Строение атома водорода в основном состоянии[править | править код]

Радиальная зависимость dp(r)/dr плотности вероятности нахождения электрона в атоме водорода, находящемся в основном состоянии, представлена на рисунке. Эта зависимость даёт вероятность того, что электрон будет обнаружен в тонком шаровом слое радиуса r толщиной dr с центром в ядре. Площадь этого слоя равна S = 4πr², его объём dV = 4πr²dr. Общая вероятность нахождения электрона в слое равна (4πr²dr) ψ², поскольку в основном состоянии волновая функция электрона сферически симметрична (то есть постоянна в рассматриваемом шаровом слое). Рисунок выражает зависимость dp(r)/dr = 4πr²ψ². Кривая радиального распределения плотности вероятности dp(r)/dr нахождения электрона в атоме водорода имеет максимум при a₀. Этот наиболее вероятный радиус совпадает с боровским радиусом. Размытое облако плотности вероятности, полученное при квантовомеханическом рассмотрении, значительно отличается от результатов теории Бора и согласуется с принципом неопределённости Гейзенберга. Это размытое сферически симметричное распределение плотности вероятности нахождения электрона, называемое электронной оболочкой, экранирует ядро и делает физическую систему протон-электрон электронейтральной и сферически симметричной — у атома водорода в основном состоянии отсутствуют электрический и магнитный дипольные моменты (как и моменты более высоких порядков), если пренебречь спинами электрона и ядра. Максимум объёмной плотности вероятности ψ² достигается не при r = a₀, как для радиальной зависимости, а при r = 0.

Атом водорода в электрическом поле[править | править код]

По теории деформационной поляризации, нейтральный атом водорода, попадая во внешнее электрическое поле, подвергается деформации — центр электронной оболочки атома водорода смещается относительно ядра на некоторое расстояние L, что приводит к появлению в атоме водорода наведённого электрического дипольного момента μ^[5]. Величина наведённого дипольного момента прямо пропорциональна напряжённости внешнего электрического поля E:

μ = α_eE = Lq

Коэффициент пропорциональности α_e носит название электронной поляризуемости. Электронная поляризуемость атома водорода составляет 0,66 Å³.^[6]

Чем выше напряжённость приложенного электрического поля, тем больше смещение центра электронной оболочки от центра атома водорода и, собственно, длина наведённого диполя:

L = α_e E/q,

где q — величина заряда ядра атома водорода.

При высоких значениях напряжённости приложенного электрического поля атом водорода подвергается ионизации полем с образованием свободных протона и электрона.

Взаимодействие атома водорода с протоном[править | править код]

Деформационная поляризация атома водорода в электрическом поле протона

Протон, обладая положительным элементарным электрическим зарядом q = 1,602•10 ⁻¹⁹ Кл, как и всякий точечный электрический заряд создаёт вокруг себя электрическое поле с напряжённостью E.
E = q/R²,
Где R — расстояние точки поля до протона.

Нейтральный атом водорода, попадая в электрическое поле протона, подвергается деформационной поляризации (см. рисунок). Длина наведённого электрического диполя атома водорода обратно пропорциональна квадрату расстояния между атомом водорода и протоном L = α_e E/q = α_e/R² = 0,66/R²

Отрицательный полюс наведённого электрического диполя атома водорода ориентируется в сторону протона. В результате чего начинает проявляться электростатическое притяжение между атомом водорода и протоном. Сближение частиц (атома водорода и протона) возможно до тех пор, пока центр плотности вероятности нахождения электрона станет равноудалённым от обоих протонов. В этом предельном случае d=R=2L. Центр области вероятного нахождения электрона совпадает с центром симметрии образовавшейся системы H₂⁺ — молекулярного иона водорода, при этом
d=R=2L=³√2α_e = ³√2•0,66 = 1,097 Å.

Найденная величина d = 1,097 Å близка к экспериментальной величине межъядерного расстояния в молекулярном ионе водорода H₂⁺ — 1,06 Å.^[7]

Взаимодействуя с протоном, атом водорода образует молекулярный ион водорода

H₂⁺,H + H ⁺ -> H₂⁺ + Q,

Характеризующийся простейшей одноэлектронной ковалентной химической связью.

Взаимодействие атома водорода с электроном[править | править код]

Деформационная поляризация атома водорода под действием приближающегося электрона и модель гидрид-иона H^–

Электрон, обладая элементарным электрическим зарядом, как и протон, создаёт вокруг себя электрическое поле, но (в отличие от электрического поля протона) с отрицательным знаком. Нейтральный атом водорода, попадая в электрическое поле электрона, подвергается деформационной поляризации. Центр электронной оболочки атома водорода смещается относительно ядра на некоторое расстояние L в противоположную сторону к приближающемуся электрону. Приближающийся электрон как бы вытесняет из атома водорода находящийся в нём электрон, подготавливая место для второго электрона. Величина смещения центра электронной оболочки атома водорода L обратно пропорциональна квадрату расстояния атома водорода к приближающемуся электрону R:

L = α_e/R² = 0.66/R² (рис)

Сближение атома водорода и электрона возможно до тех пор, пока центры областей плотностей вероятности нахождения обоих электронов не станут равноудалёнными от ядра объединённой системы — отрицательно заряженного иона водорода. Такое состояние системы имеет место при

r_e = L = R = ³√0,66 = 0,871 Å,

где r_e — орбитальный радиус двухэлектронной оболочки гидрид-иона H^–.

Таким образом, атом водорода проявляет своеобразную амфотерность: он может взаимодействовать как с положительно заряженной частицей (протоном), образуя молекулярный ион водорода H₂⁺, так и с отрицательно заряженной частицей (электроном), образуя гидрид-ион H^–.

Рекомбинация атомов водорода[править | править код]

Рекомбинация атомов водорода обсуловлена силами межатомного взаимодействия. Происхождение сил, вызывающих притяжение электрически нейтральных атомов друг к другу, было объяснено в 1930 году Ф.Лондоном. Межатомное притяжение возникает вследствие флуктуации электрических зарядов в двух атомах, находящихся близко друг от друга. Поскольку электроны в атомах движутся, то каждый атом обладает мгновенным электрическим дипольным моментом, отличным от нуля. Мгновенный диполь на одном атоме наводит противоположно направленный диполь в соседнем атоме. Наступает синхронизация колебаний двух атомов — двух осцилляторов, частоты которых совпадают. Результатом этого процесса является образование молекулы водорода.

Наличие мгновенного электрического дипольного момента у атома водорода выражается в характерной особенности атома водорода, проявляющейся в крайней реакционной способности атомарного водорода и склонности его к рекомбинации. Время существования атомарного водорода составляет около 1 с при давлении в 0,2 мм рт. ст. Рекомбинация атомов водорода имеет место, если образующаяся молекула водорода быстро освобождается от избытка энергии, выделяющейся при взаимодействии атомов водорода путём тройного столкновения. Соединение атомов водорода в молекулу протекает значительно быстрее на поверхности различных металлов, чем в самом газе. При этом металл воспринимает ту энергию, которая выделяется при образовании молекул водорода, и нагревается до очень высоких температур. Тепловой эффект реакции образования молекулярного водорода из атомов водорода составляет 103 ккал/моль.

На принципе рекомбинации атомов водорода разработана атомно-водородная сварка. Между двумя вольфрамовыми стержнями создаётся электрическая дуга, через которую по облегающим стержни трубкам пропускается ток водорода. При этом часть молекул водорода распадается на атомы, которые затем вновь соединяются на металлической поверхности, помещаемой на небольшом расстоянии от дуги. Металл может быть таким путём нагрет до температуры выше 3500° C^[8].

Константы реакции диссоциации молекулярного водорода (K_p) и степень превращения водорода в атомарное состояние (α) в зависимости от абсолютной температуры (T) представлены в таблице^[9]:

T, к	2000	3000	4000	5000	6000	8000
Кр	2,62 · 10^-6	2,47 · 10^-2	2,52	4,09 · 10	2,62 · 10²	2,70 · 10³
α	8,10 · 10^-4	7,83 · 10^-2	0,621	0,954	0,992	0,999

См. также[править | править код]

Водород
Водородоподобный атом
Квантовая механика
Квантовая химия
Квантовая теория поля
Квантовое состояние
Принцип неопределённости
Волновая функция
Электронное облако
Ридберговский атом

Примечания[править | править код]

↑ Сивухин Д. В. § 13. Спектр водорода // Общий курс физики. — М.: Наука, 1986. — Т. V. Атомная и ядерная физика. Часть 1: Атомная физика. — С. 68. — 416 с. — ISBN 5-02-014053-8.
↑ Ахметов Н. С. Неорганическая химия. Учебное пособие для вузов с ил. — 2-е изд., перераб. и доп. — М.: «Высшая школа», 1975. — 672 с.
↑ Некрасов Б. В. Курс общей химии. — 14-е изд. — М.: ГНТИ химической литературы, 1962. — С. 113. — 976 с.
↑ Даниэльс Ф., Олберти Р. Физическая химия. — пер. с англ. под ред. д. х. н., проф. К. В. Топчиевой. — М.: «Мир», 1978. — С. 369—370. — 645 с.
↑ Потапов А. А. Деформационная поляризация: Поиск оптимальных моделей. — Новосибирск: «Наука», 2004. — 511 с. — ISBN 5-02-032065-X.
↑ Справочник химика. — 2-е изд., перераб. и доп. — Л.-М.: Издательство химической литературы, 1962. — Т. 1. — С. 385. — 1071 с.
↑ Справочник химика. — 2-е изд., перераб. и доп. — Л.-М.: Издательство химической литературы, 1962. — Т. 1. — С. 388. — 1071 с.
↑ Некрасов Б. В. Курс общей химии. — 14-е изд. — М.: ГНТИ химической литературы, 1962. — С. 110. — 976 с.
↑ Справочник химика. — 2-е изд., перераб. и доп. — Л.-М.: “Химия”, 1964. — Т. 3. — С. 24. — 1008 с. — 65 000 экз.

Литература[править | править код]

Luca Nanni. The Hydrogen Atom: a Review on the Birth of Modern Quantum Mechanics (англ.). — arXiv:1501.05894.

Ссылки[править | править код]

Griffiths (англ.) (рус., David J. Introduction to Quantum Mechanics (англ.). — Upper Saddle River, NJ: Prentice Hall, 1995.
Bransden, B.H.; C.J. Joachain. Physics of Atoms and Molecules (англ.). — London: Longman, 1983.
Физика атома водорода на Scienceworld
Графическое представление орбиталей
Апплет, изображающий орбитали атома водорода

Источник

This article is about the physics of the hydrogen atom. For a chemical description, see hydrogen. For monatomic hydrogen, see Hydrogen § Atomic hydrogen.

Hydrogen atom, ¹H

General

Symbol	¹H
Names	hydrogen atom, 1H, H-1, protium
Protons (Z)	1
Neutrons (N)	0
Nuclide data
Natural abundance	99.985%
Half-life (t_1/2)	stable
Isotope mass	1.007825 Da
Spin	1/2
Excess energy	7288.969±0.001 keV
Binding energy	0.000±0.0000 keV
Isotopes of hydrogen Complete table of nuclides

Depiction of a hydrogen atom showing the diameter as about twice the Bohr model radius. (Image not to scale)

A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.^[1]

In everyday life on Earth, isolated hydrogen atoms (called “atomic hydrogen”) are extremely rare. Instead, a hydrogen atom tends to combine with other atoms in compounds, or with another hydrogen atom to form ordinary (diatomic) hydrogen gas, H₂. “Atomic hydrogen” and “hydrogen atom” in ordinary English use have overlapping, yet distinct, meanings. For example, a water molecule contains two hydrogen atoms, but does not contain atomic hydrogen (which would refer to isolated hydrogen atoms).

Atomic spectroscopy shows that there is a discrete infinite set of states in which a hydrogen (or any) atom can exist, contrary to the predictions of classical physics. Attempts to develop a theoretical understanding of the states of the hydrogen atom have been important to the history of quantum mechanics, since all other atoms can be roughly understood by knowing in detail about this simplest atomic structure.

Isotopes[edit]

The most abundant isotope, hydrogen-1, protium, or light hydrogen, contains no neutrons and is simply a proton and an electron. Protium is stable and makes up 99.985% of naturally occurring hydrogen atoms.^[2]

Deuterium (²H) contains one neutron and one proton in its nucleus. Deuterium is stable and makes up 0.0156% of naturally occurring hydrogen^[2] and is used in industrial processes like nuclear reactors and Nuclear Magnetic Resonance.

Tritium (³H) contains two neutrons and one proton in its nucleus and is not stable, decaying with a half-life of 12.32 years. Because of its short half-life, tritium does not exist in nature except in trace amounts.

Heavier isotopes of hydrogen are only created artificially in particle accelerators and have half-lives on the order of 10⁻²² seconds. They are unbound resonances located beyond the neutron drip line; this results in prompt emission of a neutron.

The formulas below are valid for all three isotopes of hydrogen, but slightly different values of the Rydberg constant (correction formula given below) must be used for each hydrogen isotope.

Hydrogen ion[edit]

Lone neutral hydrogen atoms are rare under normal conditions. However, neutral hydrogen is common when it is covalently bound to another atom, and hydrogen atoms can also exist in cationic and anionic forms.

If a neutral hydrogen atom loses its electron, it becomes a cation. The resulting ion, which consists solely of a proton for the usual isotope, is written as “H⁺” and sometimes called hydron. Free protons are common in the interstellar medium, and solar wind. In the context of aqueous solutions of classical Brønsted–Lowry acids, such as hydrochloric acid, it is actually hydronium, H₃O⁺, that is meant. Instead of a literal ionized single hydrogen atom being formed, the acid transfers the hydrogen to H₂O, forming H₃O⁺.

If instead a hydrogen atom gains a second electron, it becomes an anion. The hydrogen anion is written as “H^–” and called hydride.

Theoretical analysis[edit]

The hydrogen atom has special significance in quantum mechanics and quantum field theory as a simple two-body problem physical system which has yielded many simple analytical solutions in closed-form.

Failed classical description[edit]

Experiments by Ernest Rutherford in 1909 showed the structure of the atom to be a dense, positive nucleus with a tenuous negative charge cloud around it. This immediately raised questions about how such a system could be stable. Classical electromagnetism had shown that any accelerating charge radiates energy, as shown by the Larmor formula. If the electron is assumed to orbit in a perfect circle and radiates energy continuously, the electron would rapidly spiral into the nucleus with a fall time of:^[3]

${displaystyle t_{text{fall}}approx {frac {a_{0}^{3}}{4r_{0}^{2}c}}approx 1.6times 10^{-11}{text{ s}},}$

where $a_{0}$ is the Bohr radius and $r_{0}$ is the classical electron radius. If this were true, all atoms would instantly collapse, however atoms seem to be stable. Furthermore, the spiral inward would release a smear of electromagnetic frequencies as the orbit got smaller. Instead, atoms were observed to only emit discrete frequencies of radiation. The resolution would lie in the development of quantum mechanics.

Bohr–Sommerfeld Model[edit]

In 1913, Niels Bohr obtained the energy levels and spectral frequencies of the hydrogen atom after making a number of simple assumptions in order to correct the failed classical model. The assumptions included:

Electrons can only be in certain, discrete circular orbits or stationary states, thereby having a discrete set of possible radii and energies.
Electrons do not emit radiation while in one of these stationary states.
An electron can gain or lose energy by jumping from one discrete orbit to another.

Bohr supposed that the electron’s angular momentum is quantized with possible values:

where
and hbar is Planck constant over 2pi . He also supposed that the centripetal force which keeps the electron in its orbit is provided by the Coulomb force, and that energy is conserved. Bohr derived the energy of each orbit of the hydrogen atom to be:^[4]

${displaystyle E_{n}=-{frac {m_{e}e^{4}}{2(4pi varepsilon _{0})^{2}hbar ^{2}}}{frac {1}{n^{2}}},}$

where m_e is the electron mass, is the electron charge, $varepsilon _{0}$ is the vacuum permittivity, and is the quantum number (now known as the principal quantum number). Bohr’s predictions matched experiments measuring the hydrogen spectral series to the first order, giving more confidence to a theory that used quantized values.

For n=1 , the value^[5]

${displaystyle {frac {m_{e}e^{4}}{2(4pi varepsilon _{0})^{2}hbar ^{2}}}={frac {m_{text{e}}e^{4}}{8h^{2}varepsilon _{0}^{2}}}=1,{text{Ry}}=13.605;693;122;994(26),{text{eV}}}$

is called the Rydberg unit of energy. It is related to the Rydberg constant ${displaystyle R_{infty }}$ of atomic physics by ${displaystyle 1,{text{Ry}}equiv hcR_{infty }.}$

The exact value of the Rydberg constant assumes that the nucleus is infinitely massive with respect to the electron. For hydrogen-1, hydrogen-2 (deuterium), and hydrogen-3 (tritium) which have finite mass, the constant must be slightly modified to use the reduced mass of the system, rather than simply the mass of the electron. This includes the kinetic energy of the nucleus in the problem, because the total (electron plus nuclear) kinetic energy is equivalent to the kinetic energy of the reduced mass moving with a velocity equal to the electron velocity relative to the nucleus. However, since the nucleus is much heavier than the electron, the electron mass and reduced mass are nearly the same. The Rydberg constant R_M for a hydrogen atom (one electron), R is given by

${displaystyle R_{M}={frac {R_{infty }}{1+m_{text{e}}/M}},}$

where is the mass of the atomic nucleus. For hydrogen-1, the quantity $m_{text{e}}/M,$ is about 1/1836 (i.e. the electron-to-proton mass ratio). For deuterium and tritium, the ratios are about 1/3670 and 1/5497 respectively. These figures, when added to 1 in the denominator, represent very small corrections in the value of R, and thus only small corrections to all energy levels in corresponding hydrogen isotopes.

There were still problems with Bohr’s model:

it failed to predict other spectral details such as fine structure and hyperfine structure
it could only predict energy levels with any accuracy for single–electron atoms (hydrogen-like atoms)
the predicted values were only correct to ${displaystyle alpha ^{2}approx 10^{-5}}$ , where is the fine-structure constant.

Most of these shortcomings were resolved by Arnold Sommerfeld’s modification of the Bohr model. Sommerfeld introduced two additional degrees of freedom, allowing an electron to move on an elliptical orbit characterized by its eccentricity and declination with respect to a chosen axis. This introduced two additional quantum numbers, which correspond to the orbital angular momentum and its projection on the chosen axis. Thus the correct multiplicity of states (except for the factor 2 accounting for the yet unknown electron spin) was found. Further, by applying special relativity to the elliptic orbits, Sommerfeld succeeded in deriving the correct expression for the fine structure of hydrogen spectra (which happens to be exactly the same as in the most elaborate Dirac theory). However, some observed phenomena, such as the anomalous Zeeman effect, remained unexplained. These issues were resolved with the full development of quantum mechanics and the Dirac equation. It is often alleged that the Schrödinger equation is superior to the Bohr–Sommerfeld theory in describing hydrogen atom. This is not the case, as most of the results of both approaches coincide or are very close (a remarkable exception is the problem of hydrogen atom in crossed electric and magnetic fields, which cannot be self-consistently solved in the framework of the Bohr–Sommerfeld theory), and in both theories the main shortcomings result from the absence of the electron spin. It was the complete failure of the Bohr–Sommerfeld theory to explain many-electron systems (such as helium atom or hydrogen molecule) which demonstrated its inadequacy in describing quantum phenomena.

Schrödinger equation[edit]

The Schrödinger equation allows one to calculate the stationary states and also the time evolution of quantum systems. Exact analytical answers are available for the nonrelativistic hydrogen atom. Before we go to present a formal account, here we give an elementary overview.

Given that the hydrogen atom contains a nucleus and an electron, quantum mechanics allows one to predict the probability of finding the electron at any given radial distance . It is given by the square of a mathematical function known as the “wavefunction,” which is a solution of the Schrödinger equation. The lowest energy equilibrium state of the hydrogen atom is known as the ground state. The ground state wave function is known as the wavefunction. It is written as:

${displaystyle psi _{1mathrm {s} }(r)={frac {1}{{sqrt {pi }}a_{0}^{3/2}}}e^{-r/a_{0}}.}$

Here, $a_{0}$ is the numerical value of the Bohr radius. The probability density of finding the electron at a distance in any radial direction is the squared value of the wavefunction:

${displaystyle |psi _{1mathrm {s} }(r)|^{2}={frac {1}{pi a_{0}^{3}}}e^{-2r/a_{0}}.}$

The wavefunction is spherically symmetric, and the surface area of a shell at distance is $4pi r^{2}$ , so the total probability of the electron being in a shell at a distance and thickness is

${displaystyle P(r),dr=4pi r^{2}|psi _{1mathrm {s} }(r)|^{2},dr.}$

It turns out that this is a maximum at r = a_0 . That is, the Bohr picture of an electron orbiting the nucleus at radius $a_{0}$ corresponds to the most probable radius. Actually, there is a finite probability that the electron may be found at any place , with the
probability indicated by the square of the wavefunction. Since the probability of finding the electron somewhere in the whole volume is unity, the integral of is unity. Then we say that the wavefunction is properly normalized.

As discussed below, the ground state is also indicated by the quantum numbers . The second lowest energy states, just above the ground state, are given by the quantum numbers , , and . These n=2 states all have the same energy and are known as the and states. There is one state:

${displaystyle psi _{2,0,0}={frac {1}{4{sqrt {2pi }}a_{0}^{3/2}}}left(2-{frac {r}{a_{0}}}right)e^{-r/2a_{0}},}$

and there are three states:

${displaystyle psi _{2,1,0}={frac {1}{4{sqrt {2pi }}a_{0}^{3/2}}}{frac {r}{a_{0}}}e^{-r/2a_{0}}cos theta ,}$

${displaystyle psi _{2,1,pm 1}=mp {frac {1}{8{sqrt {pi }}a_{0}^{3/2}}}{frac {r}{a_{0}}}e^{-r/2a_{0}}sin theta ~e^{pm ivarphi }.}$

An electron in the or state is most likely to be found in the second Bohr orbit with energy given by the Bohr formula.

Wavefunction[edit]

The Hamiltonian of the hydrogen atom is the radial kinetic energy operator and Coulomb attraction force between the positive proton and negative electron. Using the time-independent Schrödinger equation, ignoring all spin-coupling interactions and using the reduced mass ${displaystyle mu =m_{e}M/(m_{e}+M)}$ , the equation is written as:

${displaystyle left(-{frac {hbar ^{2}}{2mu }}nabla ^{2}-{frac {e^{2}}{4pi varepsilon _{0}r}}right)psi (r,theta ,varphi )=Epsi (r,theta ,varphi )}$

Expanding the Laplacian in spherical coordinates:

${displaystyle -{frac {hbar ^{2}}{2mu }}left[{frac {1}{r^{2}}}{frac {partial }{partial r}}left(r^{2}{frac {partial psi }{partial r}}right)+{frac {1}{r^{2}sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial psi }{partial theta }}right)+{frac {1}{r^{2}sin ^{2}theta }}{frac {partial ^{2}psi }{partial varphi ^{2}}}right]-{frac {e^{2}}{4pi varepsilon _{0}r}}psi =Epsi }$

This is a separable, partial differential equation which can be solved in terms of special functions. When the wavefunction is separated as product of functions R(r) , , and three independent differential functions appears^[6] with A and B being the separation constants:

radial:

${displaystyle {frac {d}{dr}}left(r^{2}{frac {dR}{dr}}right)+{frac {2mu r^{2}}{hbar ^{2}}}left(E+{frac {e^{2}}{4pi varepsilon _{0}r}}right)R-AR=0}$
polar:

${displaystyle {frac {sin theta }{Theta }}{frac {d}{dtheta }}left(sin theta {frac {dTheta }{dtheta }}right)+Asin ^{2}theta -B=0}$
azimuth:

${displaystyle {frac {1}{Phi }}{frac {d^{2}Phi }{dvarphi ^{2}}}+B=0.}$

The normalized position wavefunctions, given in spherical coordinates are:

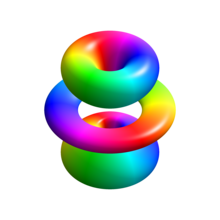
${displaystyle psi _{nell m}(r,theta ,varphi )={sqrt {{left({frac {2}{na_{0}^{*}}}right)}^{3}{frac {(n-ell -1)!}{2n(n+ell )!}}}}e^{-rho /2}rho ^{ell }L_{n-ell -1}^{2ell +1}(rho )Y_{ell }^{m}(theta ,varphi )}$

3D illustration of the eigenstate ${displaystyle psi _{4,3,1}}$ . Electrons in this state are 45% likely to be found within the solid body shown.

where:

The quantum numbers can take the following values:

Additionally, these wavefunctions are normalized (i.e., the integral of their modulus square equals 1) and orthogonal:

${displaystyle int _{0}^{infty }r^{2},drint _{0}^{pi }sin theta ,dtheta int _{0}^{2pi }dvarphi ,psi _{nell m}^{*}(r,theta ,varphi )psi _{n'ell 'm'}(r,theta ,varphi )=langle n,ell ,m|n',ell ',m'rangle =delta _{nn'}delta _{ell ell '}delta _{mm'},}$

where is the state represented by the wavefunction ${displaystyle psi _{nell m}}$ in Dirac notation, and delta is the Kronecker delta function.^[11]

The wavefunctions in momentum space are related to the wavefunctions in position space through a Fourier transform

${displaystyle varphi (p,theta _{p},varphi _{p})=(2pi hbar )^{-3/2}int e^{-i{vec {p}}cdot {vec {r}}/hbar }psi (r,theta ,varphi ),dV,}$

which, for the bound states, results in^[12]

${displaystyle varphi (p,theta _{p},varphi _{p})={sqrt {{frac {2}{pi }}{frac {(n-ell -1)!}{(n+ell )!}}}}n^{2}2^{2ell +2}ell !{frac {n^{ell }p^{ell }}{(n^{2}p^{2}+1)^{ell +2}}}C_{n-ell -1}^{ell +1}left({frac {n^{2}p^{2}-1}{n^{2}p^{2}+1}}right)Y_{ell }^{m}(theta _{p},varphi _{p}),}$

where ${displaystyle C_{N}^{alpha }(x)}$ denotes a Gegenbauer polynomial and is in units of ${displaystyle hbar /a_{0}^{*}}$ .

The solutions to the Schrödinger equation for hydrogen are analytical, giving a simple expression for the hydrogen energy levels and thus the frequencies of the hydrogen spectral lines and fully reproduced the Bohr model and went beyond it. It also yields two other quantum numbers and the shape of the electron’s wave function (“orbital”) for the various possible quantum-mechanical states, thus explaining the anisotropic character of atomic bonds.

The Schrödinger equation also applies to more complicated atoms and molecules. When there is more than one electron or nucleus the solution is not analytical and either computer calculations are necessary or simplifying assumptions must be made.

Since the Schrödinger equation is only valid for non-relativistic quantum mechanics, the solutions it yields for the hydrogen atom are not entirely correct. The Dirac equation of relativistic quantum theory improves these solutions (see below).

Results of Schrödinger equation[edit]

The solution of the Schrödinger equation (wave equation) for the hydrogen atom uses the fact that the Coulomb potential produced by the nucleus is isotropic (it is radially symmetric in space and only depends on the distance to the nucleus). Although the resulting energy eigenfunctions (the orbitals) are not necessarily isotropic themselves, their dependence on the angular coordinates follows completely generally from this isotropy of the underlying potential: the eigenstates of the Hamiltonian (that is, the energy eigenstates) can be chosen as simultaneous eigenstates of the angular momentum operator. This corresponds to the fact that angular momentum is conserved in the orbital motion of the electron around the nucleus. Therefore, the energy eigenstates may be classified by two angular momentum quantum numbers, ell and (both are integers). The angular momentum quantum number determines the magnitude of the angular momentum. The magnetic quantum number determines the projection of the angular momentum on the (arbitrarily chosen) -axis.

In addition to mathematical expressions for total angular momentum and angular momentum projection of wavefunctions, an expression for the radial dependence of the wave functions must be found. It is only here that the details of the Coulomb potential enter (leading to Laguerre polynomials in ). This leads to a third quantum number, the principal quantum number . The principal quantum number in hydrogen is related to the atom’s total energy.

Note that the maximum value of the angular momentum quantum number is limited by the principal quantum number: it can run only up to n-1 , i.e., .

Due to angular momentum conservation, states of the same ell but different have the same energy (this holds for all problems with rotational symmetry). In addition, for the hydrogen atom, states of the same but different ell are also degenerate (i.e., they have the same energy). However, this is a specific property of hydrogen and is no longer true for more complicated atoms which have an (effective) potential differing from the form (due to the presence of the inner electrons shielding the nucleus potential).

Taking into account the spin of the electron adds a last quantum number, the projection of the electron’s spin angular momentum along the -axis, which can take on two values. Therefore, any eigenstate of the electron in the hydrogen atom is described fully by four quantum numbers. According to the usual rules of quantum mechanics, the actual state of the electron may be any superposition of these states. This explains also why the choice of -axis for the directional quantization of the angular momentum vector is immaterial: an orbital of given ell and obtained for another preferred axis can always be represented as a suitable superposition of the various states of different (but same ell ) that have been obtained for .

Mathematical summary of eigenstates of hydrogen atom[edit]

In 1928, Paul Dirac found an equation that was fully compatible with special relativity, and (as a consequence) made the wave function a 4-component “Dirac spinor” including “up” and “down” spin components, with both positive and “negative” energy (or matter and antimatter). The solution to this equation gave the following results, more accurate than the Schrödinger solution.

Energy levels[edit]

The energy levels of hydrogen, including fine structure (excluding Lamb shift and hyperfine structure), are given by the Sommerfeld fine-structure expression:^[13]

${displaystyle {begin{aligned}E_{j,n}={}&-mu c^{2}left[1-left(1+left[{frac {alpha }{n-j-{frac {1}{2}}+{sqrt {left(j+{frac {1}{2}}right)^{2}-alpha ^{2}}}}}right]^{2}right)^{-1/2}right]\approx {}&-{frac {mu c^{2}alpha ^{2}}{2n^{2}}}left[1+{frac {alpha ^{2}}{n^{2}}}left({frac {n}{j+{frac {1}{2}}}}-{frac {3}{4}}right)right],end{aligned}}}$

where alpha is the fine-structure constant and is the total angular momentum quantum number, which is equal to ${displaystyle left|ell pm {tfrac {1}{2}}right|}$ , depending on the orientation of the electron spin relative to the orbital angular momentum.^[14] This formula represents a small correction to the energy obtained by Bohr and Schrödinger as given above. The factor in square brackets in the last expression is nearly one; the extra term arises from relativistic effects (for details, see #Features going beyond the Schrödinger solution). It is worth noting that this expression was first obtained by A. Sommerfeld in 1916 based on the relativistic version of the old Bohr theory. Sommerfeld has however used different notation for the quantum numbers.

Coherent states[edit]

The coherent states have been proposed as^[15]

${displaystyle |s,gamma ,{bar {Omega }}rangle equiv M(s^{2})sum _{n=0}^{infty }(s^{n}e^{igamma /(n+1)^{2}}/{sqrt {rho _{n}}})|n,{bar {Omega }}rangle ,}$

which satisfies ${displaystyle d{bar {Omega }}equiv sin {bar {theta }},d{bar {theta }},d{bar {varphi }},d{bar {psi }}/8pi ^{2}}$ and takes the form

${displaystyle {begin{aligned}langle r,theta ,varphi mid s,gamma ,{bar {Omega }}rangle ={}&e^{-s^{2}/2}sum _{n=0}^{infty }(s^{n}e^{igamma /(n+1)^{2}}/{sqrt {n!}})\&{}times ,sum _{ell =0}^{n}u_{n+1}^{ell }(r)sum _{m=-ell }^{ell }left[{frac {(2ell )!}{(ell +m)!(ell -m)!}}right]^{1/2}left(sin {frac {bar {theta }}{2}}right)^{ell -m}left(cos {frac {bar {theta }}{2}}right)^{ell +m}\&{}times ,e^{-i(m{bar {varphi }}+ell {bar {psi }})}Y_{ell m}(theta ,varphi ){sqrt {2ell +1}}.end{aligned}}}$

Visualizing the hydrogen electron orbitals[edit]

Probability densities through the xz-plane for the electron at different quantum numbers (ℓ, across top; n, down side; m = 0)

The image to the right shows the first few hydrogen atom orbitals (energy eigenfunctions). These are cross-sections of the probability density that are color-coded (black represents zero density and white represents the highest density). The angular momentum (orbital) quantum number ℓ is denoted in each column, using the usual spectroscopic letter code (s means ℓ = 0, p means ℓ = 1, d means ℓ = 2). The main (principal) quantum number n (= 1, 2, 3, …) is marked to the right of each row. For all pictures the magnetic quantum number m has been set to 0, and the cross-sectional plane is the xz-plane (z is the vertical axis). The probability density in three-dimensional space is obtained by rotating the one shown here around the z-axis.

The “ground state”, i.e. the state of lowest energy, in which the electron is usually found, is the first one, the 1s state (principal quantum level n = 1, ℓ = 0).

Black lines occur in each but the first orbital: these are the nodes of the wavefunction, i.e. where the probability density is zero. (More precisely, the nodes are spherical harmonics that appear as a result of solving the Schrödinger equation in spherical coordinates.)

The quantum numbers determine the layout of these nodes.^[16] There are:

total nodes,
of which are angular nodes:
(the remaining non-angular nodes) are radial nodes.

Features going beyond the Schrödinger solution[edit]

There are several important effects that are neglected by the Schrödinger equation and which are responsible for certain small but measurable deviations of the real spectral lines from the predicted ones:

Although the mean speed of the electron in hydrogen is only 1/137th of the speed of light, many modern experiments are sufficiently precise that a complete theoretical explanation requires a fully relativistic treatment of the problem. A relativistic treatment results in a momentum increase of about 1 part in 37,000 for the electron. Since the electron’s wavelength is determined by its momentum, orbitals containing higher speed electrons show contraction due to smaller wavelengths.
Even when there is no external magnetic field, in the inertial frame of the moving electron, the electromagnetic field of the nucleus has a magnetic component. The spin of the electron has an associated magnetic moment which interacts with this magnetic field. This effect is also explained by special relativity, and it leads to the so-called spin–orbit coupling, i.e., an interaction between the electron’s orbital motion around the nucleus, and its spin.

Both of these features (and more) are incorporated in the relativistic Dirac equation, with predictions that come still closer to experiment. Again the Dirac equation may be solved analytically in the special case of a two-body system, such as the hydrogen atom. The resulting solution quantum states now must be classified by the total angular momentum number j (arising through the coupling between electron spin and orbital angular momentum). States of the same j and the same n are still degenerate. Thus, direct analytical solution of Dirac equation predicts 2S(1/2) and 2P(1/2) levels of hydrogen to have exactly the same energy, which is in a contradiction with observations (Lamb–Retherford experiment).

There are always vacuum fluctuations of the electromagnetic field, according to quantum mechanics. Due to such fluctuations degeneracy between states of the same j but different l is lifted, giving them slightly different energies. This has been demonstrated in the famous Lamb–Retherford experiment and was the starting point for the development of the theory of quantum electrodynamics (which is able to deal with these vacuum fluctuations and employs the famous Feynman diagrams for approximations using perturbation theory). This effect is now called Lamb shift.

For these developments, it was essential that the solution of the Dirac equation for the hydrogen atom could be worked out exactly, such that any experimentally observed deviation had to be taken seriously as a signal of failure of the theory.

Alternatives to the Schrödinger theory[edit]

In the language of Heisenberg’s matrix mechanics, the hydrogen atom was first solved by Wolfgang Pauli^[17] using a rotational symmetry in four dimensions [O(4)-symmetry] generated by the angular momentum
and the Laplace–Runge–Lenz vector. By extending the symmetry group O(4) to the dynamical group O(4,2),
the entire spectrum and all transitions were embedded in a single irreducible group representation.^[18]

In 1979 the (non-relativistic) hydrogen atom was solved for the first time within Feynman’s path integral formulation
of quantum mechanics by Duru and Kleinert.^[19]^[20] This work greatly extended the range of applicability of Feynman’s method.

References[edit]

^
Palmer, D. (13 September 1997). “Hydrogen in the Universe”. NASA. Archived from the original on 29 October 2014. Retrieved 23 February 2017.
^ ^a ^b Housecroft, Catherine E.; Sharpe, Alan G. (2005). Inorganic Chemistry (2nd ed.). Pearson Prentice-Hall. p. 237. ISBN 0130-39913-2.
^ Olsen, James; McDonald, Kirk (7 March 2005). “Classical Lifetime of a Bohr Atom” (PDF). Joseph Henry Laboratories, Princeton University. Archived from the original (PDF) on 9 September 2019. Retrieved 11 December 2015.
^ “Derivation of Bohr’s Equations for the One-electron Atom” (PDF). University of Massachusetts Boston.
^ Eite Tiesinga, Peter J. Mohr, David B. Newell, and Barry N. Taylor (2019), “The 2018 CODATA Recommended Values of the Fundamental Physical Constants” (Web Version 8.0). Database developed by J. Baker, M. Douma, and S. Kotochigova. Available at http://physics.nist.gov/constants, National Institute of Standards and Technology, Gaithersburg, MD 20899. Link to R_∞, Link to hcR_∞
^ “Solving Schrödinger’s equation for the hydrogen atom :: Atomic Physics :: Rudi Winter’s web space”. users.aber.ac.uk. Retrieved 30 November 2020.
^ Messiah, Albert (1999). Quantum Mechanics. New York: Dover. p. 1136. ISBN 0-486-40924-4.
^ LaguerreL. Wolfram Mathematica page
^ Griffiths, p. 152
^ Condon and Shortley (1963). The Theory of Atomic Spectra. London: Cambridge. p. 441.
^ Griffiths, Ch. 4 p. 89
^ Bransden, B. H.; Joachain, C. J. (1983). Physics of Atoms and Molecules. Longman. p. Appendix 5. ISBN 0-582-44401-2.
^ Sommerfeld, Arnold (1919). Atombau und Spektrallinien [Atomic Structure and Spectral Lines]. Braunschweig: Friedrich Vieweg und Sohn. ISBN 3-87144-484-7. German English
^ Atkins, Peter; de Paula, Julio (2006). Physical Chemistry (8th ed.). W. H. Freeman. p. 349. ISBN 0-7167-8759-8.
^ Klauder, John R (21 June 1996). “Coherent states for the hydrogen atom”. Journal of Physics A: Mathematical and General. 29 (12): L293–L298. arXiv:quant-ph/9511033. doi:10.1088/0305-4470/29/12/002. S2CID 14124660.
^ Summary of atomic quantum numbers. Lecture notes. 28 July 2006
^
Pauli, W (1926). “Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik”. Zeitschrift für Physik. 36 (5): 336–363. Bibcode:1926ZPhy…36..336P. doi:10.1007/BF01450175. S2CID 128132824.
^
Kleinert H. (1968). “Group Dynamics of the Hydrogen Atom” (PDF). Lectures in Theoretical Physics, Edited by W.E. Brittin and A.O. Barut, Gordon and Breach, N.Y. 1968: 427–482.
^
Duru I.H., Kleinert H. (1979). “Solution of the path integral for the H-atom” (PDF). Physics Letters B. 84 (2): 185–188. Bibcode:1979PhLB…84..185D. doi:10.1016/0370-2693(79)90280-6.
^
Duru I.H., Kleinert H. (1982). “Quantum Mechanics of H-Atom from Path Integrals” (PDF). Fortschr. Phys. 30 (2): 401–435. Bibcode:1982ForPh..30..401D. doi:10.1002/prop.19820300802.

Books[edit]

Griffiths, David J. (1995). Introduction to Quantum Mechanics. Prentice Hall. ISBN 0-13-111892-7. Section 4.2 deals with the hydrogen atom specifically, but all of Chapter 4 is relevant.
Kleinert, H. (2009). Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, Worldscibooks.com, World Scientific, Singapore (also available online physik.fu-berlin.de)

External links[edit]

The Hydrogen Atom and The Periodic Table – The Feynman Lectures on Physics
Physics of hydrogen atom on Scienceworld

Источник

Точное измерение характерного размера протона принципиально важно для расчета уровней энергии и частот излучения атомов. Иллюстрация с сайта www.jlab.org

Журнал Nature опубликовал небольшую статью с результатами эксперимента, проведенного в лаборатории Томаса Джефферсона Министерства энергетики США «A small proton charge radius from an electron-proton scattering experiment» («Малый радиус заряда протона, полученный из эксперимента по электрон-протонному рассеянию»). Почему это важно.

Протон вместе с нейтронами входит в состав ядер всех известных химических элементов. С параметрами протона напрямую связаны некоторые фундаментальные физические постоянные. В частности, постоянная Ридберга, используемая для расчета уровней энергии и частот излучения атомов. Специальная международная комиссия CODATA отслеживает все результаты измерений фундаментальных констант. Теперь работы экспертам комиссии прибавится.

Протон почти не виден

Польскому поэту и философу Станиславу Ежи Лецу принадлежит замечательный афоризм: «И размеры Вселенной могут быть военной тайной». Недаром английский астрофизик Стивен Хокинг в 1990 году подчеркивал: «Очень трудно доказать беспредельность Вселенной, но если мы это сделаем, то сможем объяснить все во Вселенной, основываясь на гипотезе о ее беспредельности, и я думаю, что такая теория будет более экономной и более естественной». Но как минимум неменьшая тайна – размеры объектов на другом конце шкалы масштабов: атомы, не говоря уже об элементарных частицах. И квантовая физика, изучающая эти объекты, существование которых зачастую и представить можно только в виде математической формулы, тоже претендует на объяснение всего во Вселенной.

Действительно, если астрофизические события и объекты мы можем наблюдать и/или визуализировать непосредственно, хотя и с задержкой, порой в миллиарды лет, то получить изображение элементарных частиц не удается принципиально. Не удавалось…

Еще каких-то 10 лет назад можно было, не покривив против «истины» (беру в кавычки, так как абсолютная истина – это все-таки идеальная модель), сказать: «До сих пор считалось, что сфотографировать атом водорода нет никакой технической и технологической возможности. Недаром в современных учебных пособиях для студентов можно прочитать, что «…атомы лежат за пределами нашего восприятия, их нельзя ни увидеть, ни услышать. Атомистические представления не могут возникнуть и из мифа, поскольку миф всегда использует наглядные образы» (см. «НГ-науку» от 24.11.10).

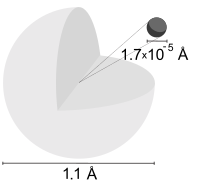
Но как раз в 2010 году физики из Токийского университета сумели впервые в истории сфотографировать отдельный атом водорода. Достижение феноменальное и, казалось, предельное. Проще атома водорода вроде бы природа ничего не создала. Ядро, роль которого играет положительно заряженная элементарная частица, – протон, а вокруг «размыт» по орбите отрицательно заряженный электрон. Диаметр атома водорода примерно 10–8 см, размеры ядра – 10–13 см. Представьте себе, что электрон вращается вокруг шпиля Московского государственного университета им. М.В. Ломоносова с диаметром орбиты вращения 1 км. Тогда размеры ядра атома на шпиле – не более горошины.

И вот в минувшем ноябре журнал Nature сообщает очередную порцию новостей об… устройстве этой самой «горошины».

До 2010 года измерения радиуса протона проводились двумя методами: рассеяния электронов и атомной спектроскопии. В экспериментах по рассеянию электронов радиус заряда протона определяется по изменению пути электронов после того, как они отразились или рассеялись от протона (упругое электрон-протонное рассеяние). В измерениях методом атомной спектроскопии фиксируются переходы между энергетическими уровнями электронов, вращающихся вокруг ядра водорода или дейтерия. Оба эти метода давали значение радиуса протона около 0,88 фемтометра.

Для постановки нового эксперимента по
измерению радиуса протона пришлось
существенно модернизировать ускоритель
непрерывных электронных пучков CEBAF.
Фото с сайта www.jlab.org

В 2010 году физики опробовали новый вариант метода атомной спектроскопии, заменив электроны на мюоны, которые вращаются намного ближе к протону и более чувствительны к радиусу заряда последнего. Этот результат дал значение, которое было на 4% меньше: примерно 0,84 фемтометра. «…Новый метод с использованием мюонных атомов водорода обнаружил существенное расхождение по сравнению с предыдущими результатами, которые стали называться «загадкой радиуса протона», – пишут авторы статьи в Nature. – Несмотря на экспериментальные и теоретические усилия, загадка остается нерешенной. Фактически существует несоответствие между двумя самыми последними спектроскопическими измерениями, проведенными на обычном водороде».

Тогда стали писать о том, что, возможно, мюоны взаимодействуют с протонами не так, как электроны, и это открывает окно в «новую физику», а сам факт несходимости результатов измерений и назвали «головоломкой протонного радиуса». Для наглядности – хотя о какой наглядности здесь можно говорить! – один фемтометр – это 10–15 метра.

При этом протон и электрон в атоме водорода гравитационно притягиваются с силой, которая составляет всего лишь 4 х 10–40 от силы их электростатического притяжения.

А пятому – не бывать!

Надо сказать, что подготовка к новому эксперименту по разгадыванию этой головоломки заняла у американских ученых семь лет.

В 2012 году группа ученых под руководством Ашота Гаспаряна из Университета штата Северная Каролина собралась в лаборатории Томаса Джефферсона Министерства энергетики США, чтобы доработать метод рассеяния электронов. Эксперимент получил название PRad («Протонный радиус»). Специально была проведена модернизация ускорительного комплекса CEBAF (Continuous Electron Beam Accelerator Facility – ускоритель непрерывных электронных пучков). Методика PRad предусматривала три нововведения.

Во-первых, был разработан новый тип мишени. Охлажденный газообразный водород направлялся прямо в поток ускоренных электронов с энергией 1,1 и 2,2 ГэВ, что позволило рассеянным электронам двигаться почти беспрепятственно в детекторы.

Во-вторых, для детектирования рассеянных электронов, возникающих в результате попадания электронов на протоны или электроны водорода, применили калориметр, а не традиционный магнитный спектрометр. Гибридный калориметр HyCal измерял энергию и положение рассеянных электронов, в то время как газовый электронный детектор GEM, специально построенный для этого эксперимента, определял позиции электронов, но с высокой точностью. Данные обоих детекторов сравнивались в реальном времени. Это дало возможность экспериментаторам понять, какое событие они обнаружили: электрон-электронное или электрон-протонное рассеяние. Понятно, что это значительно повысило точность эксперимента.

Были применены и еще некоторые, сугубо технологические, ухищрения, про которые можно сказать – искусство эксперимента.

В итоге полученный по новой методике радиус протона составляет 0,831 ± 0,007 фемтометра. Это самое точное значение на сегодняшний день. Оно меньше, чем предыдущее значение, полученное методом рассеяния электронов (0,88 фемтометра), и неплохо согласуется с результатами мюонной атомной спектроскопии (0,84 фемтометра).

«Мы рады, что годы напряженной работы нашего сотрудничества заканчиваются хорошим результатом, который поможет в решении так называемой головоломки протонного радиуса», – приводит слова Ашота Гаспаряна пресс-релиз Министерства энергетики США.

В самой статье авторы подчеркивают: «Кроме того, наш вывод согласуется с пересмотренным значением (объявленным в 2019 году. – «НГ-наука») для постоянной Ридберга – одной из наиболее точно оцененных фундаментальных констант в физике».

«Это было самое сложное измерение, которое когда-либо пыталась сделать наша лаборатория. Мы добились высочайшего уровня точности в измерении радиуса протона, – отметил ведущий автор исследования, сотрудник департамента физики и астрономии Йоркского университета Эрик Хессельс. – После восьми лет работы над этим экспериментом мы все же смогли провести такое высокоточное измерение, которое помогает решить головоломку протонного радиуса».

Поиск решения этой загадки имеет далеко идущие последствия для понимания законов физики, таких как теория квантовой электродинамики, которая описывает, как взаимодействуют свет и материя.

Опять же это важно хотя бы потому, что разброс в измерениях радиуса протона привел к появлению гипотезы о существовании некоей новой фундаментальной силы природы (отсюда и разговоры о «новой физике»), по-разному действующей на электроны и мюоны. Напомним, сегодня известны четыре фундаментальных взаимодействия в природе: сильное, электромагнитное, слабое и гравитационное. А пятому – не бывать! По крайней мере пока.

Тотальная визуализация

Но достижение американских физиков имеет не только сугубо естественно-научное значение – хотя, подчеркнем еще раз, даже сами по себе экспериментальная техника и методология просто удивительны, – но и мировоззренческое, философское значение.

«Человек способен понять вещи, которые он уже не в силах вообразить», – отмечал в свое время нобелевский лауреат Лев Ландау, рассуждая о квантовой механике. И все-таки перевести объекты в изображения – это неистребимая потребность физиков. Соответственно, изобразить нечто, непредставимое в образах принципиально, считалось невозможным. Вернее, эти изображения не могут нести никакого физического смысла и не соответствуют реальному физическому объекту. В общем, материя – это то, что поддается записи математическими формулами. И это – давняя философская традиция. Иммануил Кант, например, считал, что «…в любом частном учении о природе можно найти науки в собственном смысле лишь столько, сколько имеется в ней математики».

«…Начиная с середины 1980-х годов некоторые наиболее интересные и значимые изображения в науке оказываются совершенно неадекватными тем объектам, которые они пытаются репрезентировать… репрезентируют скорее породившую их математику, чем любые изображаемые объекты в пространстве, – пишет профессор Чикагского института искусств Джеймс Элкинс в эссе «Бесполезная визуализация квантовой механики» («Исследуя визуальный мир», Вильнюс, 2010). – В моем визуальном воображении нет ничего соответствующего бариону с его валентностью и морским кварком. Также я не имею ментального изображения электрона, даже оставляя в стороне дозволенные количества спиновых моментов импульсов».

И тем не менее магистральная линия в науке (не только в физике) – визуализация концептов, результатов, гипотез. Хрестоматийный пример «визуализации» непредставимого, но измеримого – ньютоновский закон всемирного тяготения. Ньютону удалось сделать главное – найти образ, который стал наглядным, а потому и запоминающимся, визуальным символом новой загадочной силы – гравитации. Этот образ и материализовался в падающем яблоке…

Вот и с электронами интересная получается картинка…

В 2011 году физики из Имперского колледжа Лондона сообщили, что им удалось определить форму электрона с точностью, которая на много порядков превосходит точность всех сделанных ранее измерений.

Электрон – элементарная частица, отвечающая за перенос электромагнитного взаимодействия. Существующие теории предполагают, что электрон должен иметь практически идеальную сферическую форму. Однако провести точные измерения этого параметра невероятно сложно. Как отмечалось в пресс-релизе Имперского колледжа Лондона, подготовка и проведение эксперимента заняли около 10 лет. С помощью лазерной системы ученые измеряли малейшие колебания, которые совершали находящиеся в молекулах фторида иттербия электроны. В итоге было установлено, что отклонения от идеальной сферической формы в электроне не превышают 10–28 см. Если увеличить размер электрона до размеров Солнечной системы, то размер отклонений окажется меньше толщины человеческого волоса.

В 2015 году международная команда исследователей из России, Дании, Бельгии и Канады под руководством Ганса Якоба Вернера из Высшей технической школы в Цюрихе смогла проследить движение электронов в молекуле с временным разрешением 100 аттосекунд и показала, что этими электронами можно управлять. (Приставка «атто» означает 10–18 с.)…

Итак, фотографию атома водорода мы уже давно имеем. Шарообразность электрона подтверждена с умопомрачительной точностью; само движение электрона отслежено с не менее обескураживающими подробностями. Возможно, нынешнее беспрецедентное измерение характерного размера протона станет тем рубежом в истории науки, пройдя который придется вообще отказаться от понятия «принципиально неизобразимый объект (явление)». Или по крайней мере значительно раздвинет пределы репрезентации физических концептов. Теперь это не только математические формулы, но и картинки. Недаром древние греки не различали понятий «видеть» и «знать».

Источник

Каков диаметр атома водорода и каков диаметр протона в атоме водорода?

Сейчас на главной

Новости

Публикации

Решение уравнения Шрёдингера[править | править код]

Математическое описание атома водорода[править | править код]

Энергетический спектр[править | править код]

Волновые функции[править | править код]

Угловой момент[править | править код]

Нахождение энергии электрона из модели Бора[править | править код]

Визуализация орбиталей атома водорода[править | править код]

Строение и свойства атома водорода[править | править код]

Образование атома водорода и его спектр излучения[править | править код]

Возбуждение и ионизация атома водорода[править | править код]

Строение атома водорода в основном состоянии[править | править код]

Атом водорода в электрическом поле[править | править код]

Взаимодействие атома водорода с протоном[править | править код]

Взаимодействие атома водорода с электроном[править | править код]

Рекомбинация атомов водорода[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Isotopes[edit]

Hydrogen ion[edit]

Theoretical analysis[edit]

Failed classical description[edit]

Bohr–Sommerfeld Model[edit]

Schrödinger equation[edit]

Wavefunction[edit]

Results of Schrödinger equation[edit]

Mathematical summary of eigenstates of hydrogen atom[edit]

Energy levels[edit]

Coherent states[edit]

Visualizing the hydrogen electron orbitals[edit]

Features going beyond the Schrödinger solution[edit]

Alternatives to the Schrödinger theory[edit]

See also[edit]

References[edit]

Books[edit]

External links[edit]

Вам также может понравиться

Как найти человека через школу

Superfetch ошибка как исправить

Как найти объем оксида азота

Добавить комментарий Отменить ответ