Как найти диаметр конуса если известна образующая

Найди верный ответ на вопрос ✅ «Как найти диаметр основания конуса*помогите если длинна оброзующей 37 высота конуса = 12 …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.

Круглый прямой конус

В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая – директрисой, или направляющей.

Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.

Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.

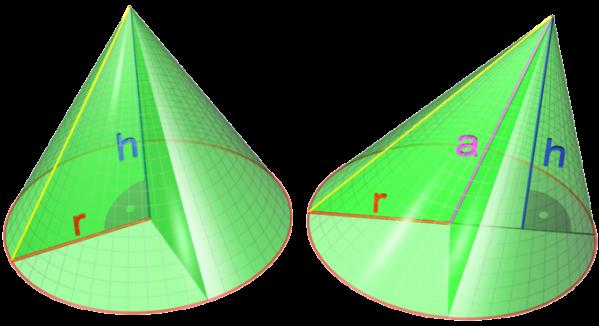
Здесь r – радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.

Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая – это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.

Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.

Вычисление диаметра фигуры через линейные параметры и угол при основании

Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.

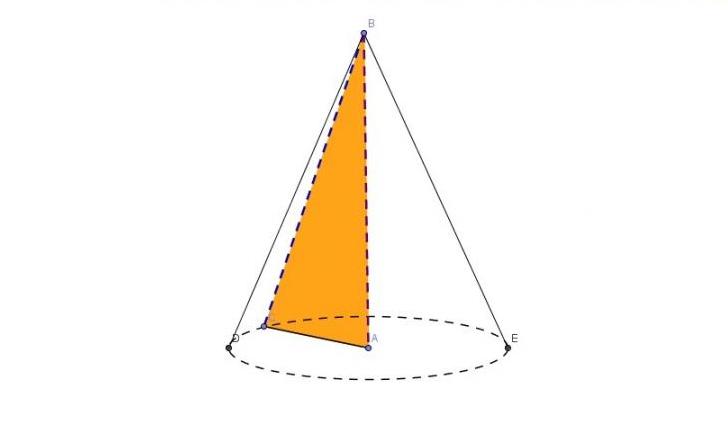
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g – это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:

d = 2*√(g² – h²)

При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.

Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:

d = 2*g*cos(φ);

d = 2*h/tg(φ)

Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.

Вычисление диаметра через площадь поверхности и генератрису

Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.

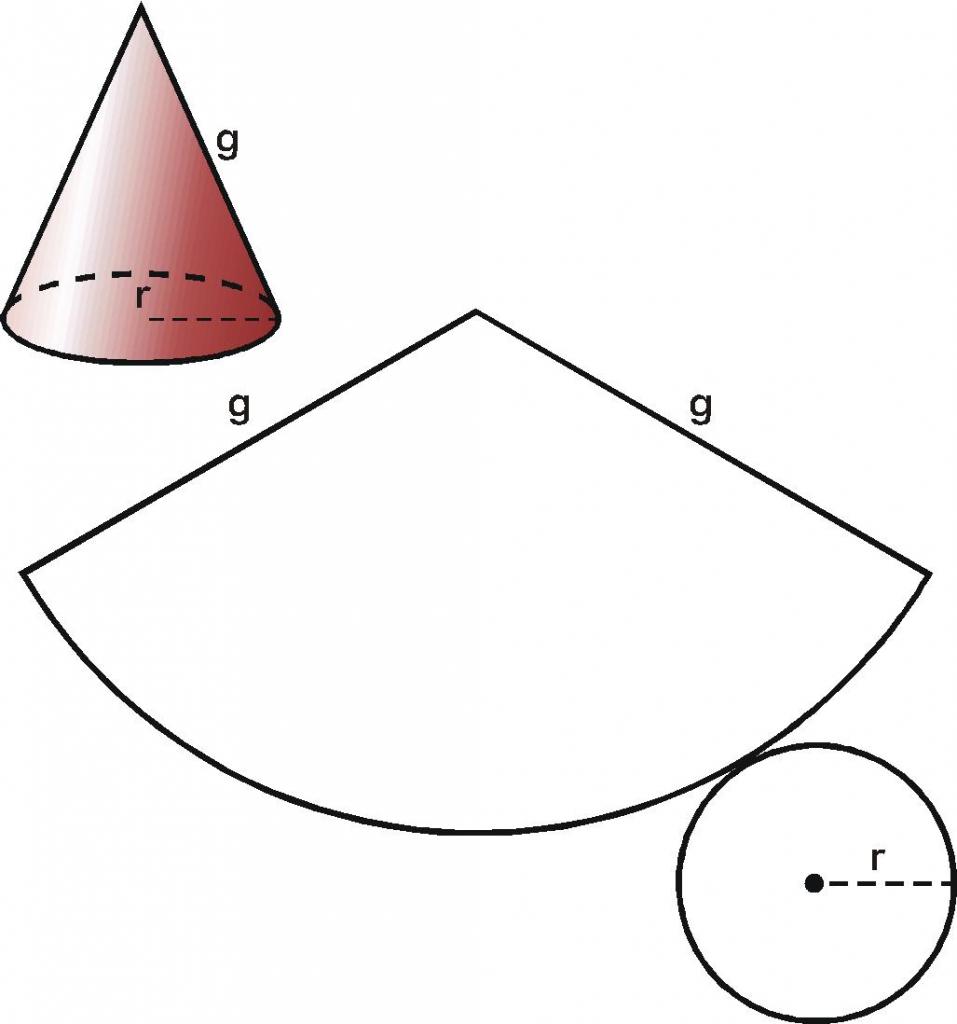
Общая площадь развертки определяется по следующей формуле:

S = pi*r² + pi*r*g

Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.

С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.

Определение диаметра через объем и высоту

Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:

V = 1/3*S*h

Здесь S – площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:

V = 1/3*pi*r²*h

Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:

r = √(3*V/(pi*h));

d = 2*r = 2*√(3*V/(pi*h))

Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.

Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.

Задача на определение диаметра через известную площадь конуса и его образующую

Дан конус, площадь поверхности которого составляет 150 см². Генератриса равна 14 см. Чему равен диаметр конуса?

Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:

S = pi*r² + pi*r*g =>

r² + 14*r – 150/3,14 = 0

При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:

D = 14² – 4*1*(-150/3,14) = 387,0828

Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:

r = (-14±√D)/2

Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:

r = (-14+√387,0828)/2 = 2,837 см

Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.

В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.

Как найти диаметр окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.

Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.

Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.

Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.

Радиус — отрезок, который соединяет центр окружности и любую точку на ней.

Как узнать диаметр. Формулы

В данной теме нам предстоит узнать три формулы:

1. Общая формула.

Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.

2. Если перед нами стоит задача найти диаметр по длине окружности

D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.

3. Если есть чертеж окружности

• Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.

• Отметить точки пересечения прямой и окружности.

• Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.

• Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.

• Теперь осталось измерить диаметр круга при помощи линейки. Получилось!

Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.

Формулы для вычисления диаметра конуса. Пример решения геометрической задачи

Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.

Круглый прямой конус

В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая – директрисой, или направляющей.

Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.

Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.

Здесь r – радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.

Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая – это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.

Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.

Вычисление диаметра фигуры через линейные параметры и угол при основании

Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.

Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g – это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:

При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.

Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:

Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.

Вычисление диаметра через площадь поверхности и генератрису

Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.

Общая площадь развертки определяется по следующей формуле:

Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.

С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.

Определение диаметра через объем и высоту

Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:

Здесь S – площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:

Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:

Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.

Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.

Задача на определение диаметра через известную площадь конуса и его образующую

Дан конус, площадь поверхности которого составляет 150 см 2 . Генератриса равна 14 см. Чему равен диаметр конуса?

Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:

r 2 + 14*r – 150/3,14 = 0

При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:

Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:

Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:

Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.

В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.

Как найти диаметр основания окружности

Как найти диаметр окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.

Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.

Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.

Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.

Радиус — отрезок, который соединяет центр окружности и любую точку на ней.

Как узнать диаметр. Формулы

В данной теме нам предстоит узнать три формулы:

1. Общая формула.

Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.

2. Если перед нами стоит задача найти диаметр по длине окружности

D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.

3. Если есть чертеж окружности

• Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.

• Отметить точки пересечения прямой и окружности.

• Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.

• Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.

• Теперь осталось измерить диаметр круга при помощи линейки. Получилось!

Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.

Радиус и диаметр окружности

Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).

Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.

Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности

Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.

Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.

На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;

Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.

Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.

Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.

Формула радиуса окружности через диаметр:

Формула диаметра окружности через радиус:

Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.

Существует радиус вписанной окружности
и радиус описанной окружности.

Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.

Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.

Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.

Как посчитать диаметр окружности

Онлайн калькулятор

Как посчитать диаметр зная длину окружности

Чему равен диаметр если длина окружности ?

Каков диаметр (d) если длина окружности C?

Формула

d = C /_π , где π ≈ 3.14

Пример

Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.

Как посчитать диаметр зная радиус окружности

Чему равен диаметр окружности если

Каков диаметр окружности (d) если её радиус r?

Формула

Пример

Если радиус круга равен 0.5 см, то его диаметр равен 1 см.

Как посчитать диаметр окружности зная её площадь

Чему равен диаметр окружности если

Каков диаметр окружности (d) если её площадь S?

Формула

d = √ 4S /_π , где π ≈ 3.14

Пример

Если площадь круга равна 5 см 2 , то его диаметр примерно равен 2.52 см.

[spoiler title=”источники:”]

http://fb.ru/article/446998/formulyi-dlya-vyichisleniya-diametra-konusa-primer-resheniya-geometricheskoy-zadachi

http://b4.cooksy.ru/articles/kak-nayti-diametr-osnovaniya-okruzhnosti

[/spoiler]

Задания

Версия для печати и копирования в MS Word