Радиус и диаметр окружности
Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).
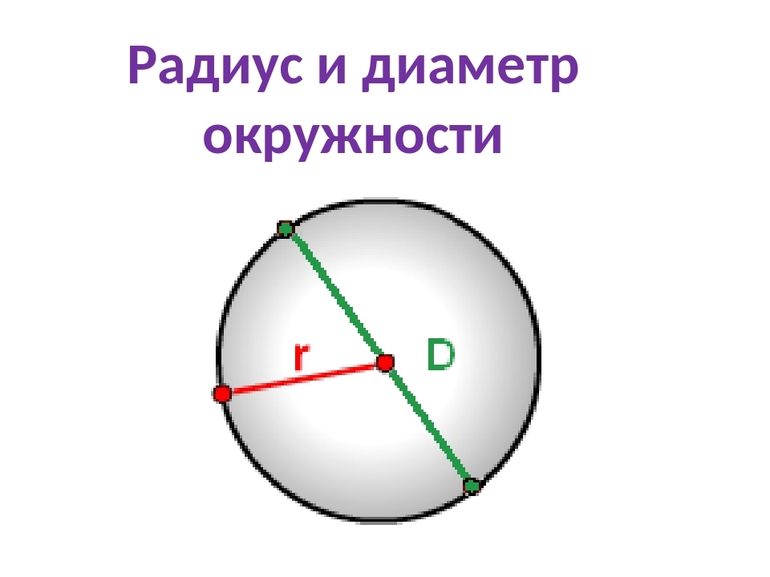
Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.
Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности
Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.
Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.
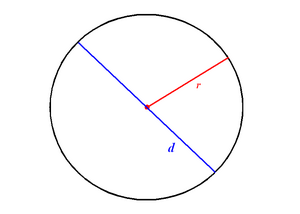
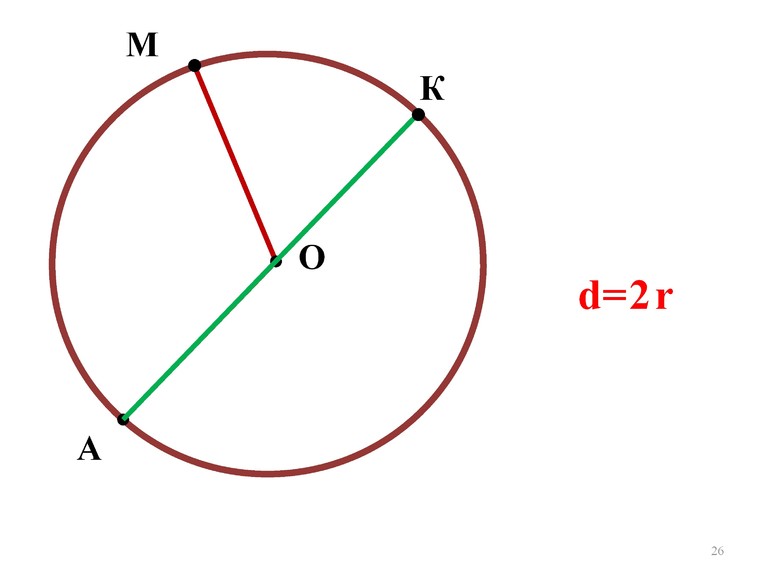
На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;
Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.
Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.
Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.
Формула радиуса окружности через диаметр:
Формула диаметра окружности через радиус:
Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.
Существует радиус вписанной окружности
и радиус описанной окружности.
Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.
Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.
Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.
Как найти диаметр окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Что такое окружность: определение, свойства, формулы
В данной публикации мы рассмотрим определение и свойства одного из основных геометрических объектов – окружности. Также приведем формулы, с помощью которых можно найти ее радиус, диаметр и длину.
Определение окружности
Окружность – это замкнутая кривая на плоскости, состоящая из точек, равноудаленных от определенной точки. Данная точка называется центром окружности.
Радиус окружности (R) – это отрезок, соединяющий любую точку, лежащую на окружности, с ее центром.
Диаметр окружности (d) – это линия (хорда), проходящая через центр окружности и соединяющая две противоположные точки, лежащие на ней.
Примечание: Не стоит путать окружность с кругом, т.к. круг – это множество точек плоскости, ограниченных окружностью (т.е. лежащих внутри окружности).
Свойства окружности
Свойство 1
Через три точки на плоскости, не лежащие на одной прямой, можно провести окружность, причем только одну.
Свойство 2
Точка касания двух окружностей (C) лежит на одной прямой (AB), которая проходит через их центры.
Свойство 3
Изопериметрическое неравенство: Из всех замкнутых кривых одинаковой длины окружность ограничивает область с самой большой площадью.
Формулы
1. Диаметр окружности (d):
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/diametr-okruzhnosti
[/spoiler]
Диа́метр (фр. diamètre из лат. diametrus из др.-греч. διάμετρος — поперечник[1]) — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Обобщённо диаметром фигуры (множества) называется максимальное расстояние между точками этой фигуры (множества), или точная верхняя грань всевозможных расстояний, если максимальное не существует.
Диаметр геометрических фигур[править | править код]
Радиус (r) и диаметр (d) окружности
Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.
Символ диаметра[править | править код]
Символы со сходным начертанием: Ø · ø · ∅
В инженерной графике и технических спецификациях диаметр принято обозначать символом [2].
Символ диаметра представлен в Юникоде (U+2300 ⌀ diameter sign)[3] и, хотя он отсутствует в стандартных раскладках клавиатуры, может быть введён с клавиатуры:
- в HTML как
⌀или⌀ - в LaTeX для его отображения предназначена команда
diameterиз пакета wasysym - в Microsoft Word символ можно получить, введя 2300 и нажав Alt+X
- в Windows с помощью Alt-кода Alt+8960 (в английской раскладке)
- в системах, использующих X Window System (Unix/Linux/ChromeOS и др.), с помощью комбинации Ctrl+⇧ Shift+u 2300Пробел или с использованием клавиши Compose, нажав поочерёдно Composedi[4].
Также, символ можно найти и скопировать в приложениях и инструментах типа «таблица символов», например:
- в Windows — Таблица символов[en]
- в программах из пакета Microsoft Office — меню «Вставка» → «Символ…»
- в macOS — Character Palette/Viewer (вызывается комбинацией ⌥ Opt+⌘ Cmd+T)
- в GNOME — Таблица символов GNOME (ранее — gucharmap).
Во многих случаях символ диаметра может не отображаться, так как его редко включают в шрифты (он присутствует, например, в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других), в связи с чем вместо него часто используются другие символы со схожим начертанием. К примеру, в САПР AutoCAD вместо символа диаметра используется символ пустого множества (U+2205 ∅ empty set), вводящийся сочетанием %%c (буква c — латинская) или U+2205 в текстовой строке. Взаимозаменяемость этих символов отражена и в стандартах консорциума W3C[5]. Также, для замены часто используется буква Ø датско-норвежского алфавита.
Сопряжённые диаметры эллипса и гиперболы[править | править код]
Сопряжённые диаметры эллипса[править | править код]
Пара сопряжённых диаметров эллипса. Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм
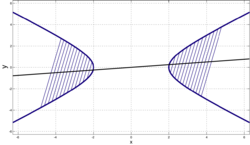
- Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
На рисунке представлена пара сопряжённых диаметров (красный и синий). Если в точках пересечения диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зелёные линии на рисунке).
Сопряжённые диаметры гиперболы[править | править код]
-
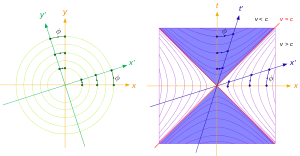
Для произвольного угла φ показаны диаметры и сопряжённые им диаметры для окружностей и равнобочных гипербол.
-
- Если диаметр гипербол a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными.
- Главными диаметрами гипербол называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
- В случае гипербол с асимптотами, образующими прямой угол, её сопряжённые гиперболы получатся при её зеркальном отражении относительно одной из асимптот. При таком зеркальном отражении её диаметр перейдет в сопряжённый диаметр, который будет просто диаметром сопряжённой гиперболы (см. рис.). Также. как наблюдается перпендикулярность сопряжённых диаметров на окружности (на рис. слева), аналогичная ортогональность наблюдается для сопряжённых диаметров гиперболы со взаимно перпендикулярными асимптотами (на рис. справа).
Вариации и обобщения[править | править код]
Понятие диаметра допускает естественные обобщения на некоторые другие геометрические и математические объекты. Если во множестве некоторых объектов определена метрика пространства, то для подмножества этих объектов может быть введено понятие диаметра множества.
Диаметром множества 


Под диаметром метрического пространства понимается точная верхняя грань расстояний между парой любых его точек.
- В частности:
Например, диаметр n-размерного гиперкуба со стороной s равен
.
Некоторые окружности, построенные в треугольнике на одном отрезке, как на диаметре[править | править код]
- Окружность Фурмана построена на одном отрезке, как на диаметре
- Окружность Брокара построена на одном отрезке, как на диаметре
См. также[править | править код]
- Радиус
- Пи
- При делении фигур на части меньшего диаметра возникла гипотеза Борсука, опровергнутая в 1993 году
- Изодиаметрическое неравенство
- Угловой диаметр астрономических объектов.
- Диаметр циркуляции
- Гидравлический диаметр
Примечания[править | править код]
- ↑ диаметр // Этимологический словарь русского языка = Russisches etymologisches Wörterbuch : в 4 т. / авт.-сост. М. Фасмер ; пер. с нем. и доп. чл.‑кор. АН СССР О. Н. Трубачёва, под ред. и с предисл. проф. Б. А. Ларина [т. I]. — Изд. 2-е, стер. — М. : Прогресс, 1986—1987.
- ↑
Большаков В. П., Тозик В. Т., Чагина А. В. Инженерная и компьютерная графика. — СПб.: БХВ-Петербург, 2013. — 288 с. — ISBN 978-5-9775-0422-5. — С. 90. - ↑ The Unicode Standard, Version 13.0. Miscellaneous Technical, Range: 2300–23FF (англ.) (PDF). Unicode Inc[en] (2020). Дата обращения: 6 сентября 2020. Архивировано 30 декабря 2019 года.
- ↑ Monniaux, David UTF-8 (Unicode) compose sequence (англ.). — Файл конфигурации вводимых с помощью клавиши Compose символов. Дата обращения: 6 сентября 2020. Архивировано 3 августа 2020 года.
- ↑ SYMBOL Characters and Glyphs. Дата обращения: 6 сентября 2020. Архивировано 6 августа 2020 года.
Литература[править | править код]
- Диаметр // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Download Article
Download Article
Need to find the diameter of a circle? Calculating diameter is easy—you just need the radius, the circumference, or the area. Even if you don’t have any of those dimensions, you can still find the diameter if you have a drawing of the circle. Keep reading to learn all of the different formulas you can use to find the diameter of a circle, examples included.
Calculation Help
-
1
If you know the radius of the circle, double it to get the diameter. The radius is the distance from the center of the circle to its edge.[1]
Example
If the radius of the circle is 4 cm, then the diameter of the circle is 4 cm x 2, or 8 cm. -
2
Example
If the circumference of the circle is 10 cm, then the diameter is 10 cm/π, or 3.18 cm.Advertisement
-
3
If you know the area of the circle, divide the result by π and find its square root to get the radius; then multiply by 2 to get the diameter. This goes back to manipulating the formula for finding the area of a circle, A = πr2, to get the diameter. You can transform this into r = √(A/π) cm.[3]
Example
If the area of the circle is 25 cm2, divide that by π and find the square root.
This equals cm 2.82cm, so the diameter of the circle is 2.82 x 2 = 5.64cm.
Advertisement
-
1
Draw a horizontal line inside the circle from one edge to the other. Use a ruler or a straight edge to do this.
It can be at the top, near the bottom, or anywhere in between.
-
2
Label the points where the line crosses the circle points “A” and “B.”
-
3
Draw two overlapping circles, one using A as the center and the other using B as the center. Be sure the two circles overlap like a Venn diagram.
-
4
Draw a vertical line through the two points at which the outer circles intersect. This line marks the diameter of the circle4.
-
5
Measure the diameter.
Measure it using a ruler,
or for greater accuracy, a pair of digital calipers. You’re done!
Advertisement
Add New Question
-
Question
What is diference between radius and diameter?
The radius is half the diameter.
-
Question
If I have the circumference, how can I calculate diameter?
Divide the circumference by pi.
-
Question
The radius of a dinner plate is 6 cm; what is the diameter?
Since the radius is half the diameter, to get the diameter, you’d multiply the 6 cm by 2. The diameter of this circular dinner plate is 12 cm.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Familiarize yourself with the use of a compass (the drawing tool, not the direction-finder). This is a very useful instrument in many applications, including drawing a circle’s diameter, as outlined above. A divider (an instrument similar to a compass) can sometimes be used in such cases.[4]
-
Using geometrical formulas and equations gets easier with practice. Ask for help from someone who has worked with circles or any other geometrical figures. You’re likely to find that questions of geometry will seem less challenging with a little experience.
Thanks for submitting a tip for review!
Advertisement
Things You’ll Need
- Calculator
- Pencil with an eraser
- Compass
- Ruler
- Digital calipers(optional)
References
About This Article
Article SummaryX
The diameter of a circle is the distance straight across the circle from one side to the other at its center. Depending on what other information you have about the circle, there are a few different ways to calculate the diameter. If you know the radius of the circle, all you have to do is multiply it by 2 to get the diameter. For instance, a circle with a radius of 2 cm would have a diameter of 4 cm. You can also find the diameter of a circle if you know its circumference, or the distance all the way around the outside of the circle. Just divide the circumference by π to find the diameter. For example, if your circle has a circumference of 23 inches, the diameter would be 23/π, or approximately 7.32 inches. If you only know the area of the circle, use the formula diameter = 2 x √(area/π). So, if the area of the circle is 25 square centimeters, the diameter would be 2 x √(25/π), or approximately 5.64 centimeters. You can also measure the diameter of a drawing of a circle, but you’ll need to find the exact center of the circle to make an accurate measurement. The easiest way to do this is to draw two parallel chords across the circle. A chord is a straight line that connects any two points on the outer edge of the circle. Once you’ve drawn your chords, draw a diagonal line starting at the point where one chord intersects the edge of the circle, then connect it to the opposite point on the chord below. Draw a second line crossing the first one, connecting the other two points of the chords. The point where the two lines intersect will be the exact center of the circle. Draw a line through that point from one side of the circle to the other, and measure the length of that line to get the diameter. Read the article to learn how to calculate the diameter of a circle using a ruler!
Did this summary help you?
Thanks to all authors for creating a page that has been read 3,830,264 times.
Did this article help you?
Обновлено: 19.05.2023
В школьных задачах за шестой класс обязательно есть задания по поиску диаметра круга или шара. В статье мы подробно рассмотрим этот вопрос и способы его решения.
О чем эта статья:
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
Отметить точки пересечения прямой и окружности.
Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Диаметр в изначальном значении это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Содержание
Диаметр геометрических фигур
Диаметр окружности, круга, сферы, шара
Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), и проходящий через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет максимальную длину. По величине диаметр равен двум радиусам.
Символ диаметра
Вариации и обобщения
Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты.
- Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
- Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:
- Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга.
- Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.
- Диаметром множества, лежащего в метрическом пространстве с метрикой , называется величина rho(x, y))” width=”” height=”” />
. Например, диаметр n-размерного гиперкуба со стороной s равен
На практике в жизни с окружностью сталкивается каждый человек. Это может быть обруч, который крутят на уроке физкультуры либо на занятиях фитнеса, а также арена цирка либо просто украшение на пальце — кольцо. Радиус и диаметр окружности — взаимосвязанные математические понятия, которые необходимо выучить детям в школьной программе еще в начальной школе.
Определения понятий
Чтобы изобразить фигуру, достаточно обвести контур карандашом вокруг круглого предмета либо начертить при помощи циркуля. На месте прокола циркуля ставят точку, что и будет центром окружности.
Если поставить точку на окружности и соединить ее с центром, в результате получится отрезок. Таких отрезков можно нарисовать не один, сколько точек на окружности поставить — столько и будет таких отрезков, то есть бесчисленное количество.
Отрезок, который равен расстоянию от центра до границ окружности имеет название радиуса. Этот термин с латинскими корнями и в переводе означает луч либо спица колеса.
Диаметром называется отрезок, который соединяет 2 точки окружности и проходит обязательно через центр круга. Такой отрезок делит круг на 2 части. По-другому — хорда, которая проходит через центр круга. Этот отрезок самый больший, который можно изобразить в круге, что и будет отличаться от других отрезков. Их можно изобразить в фигуре бесконечное число.
Обозначения и свойства
Понятия имеют принятые обозначения. Буквой d обозначают диаметр (в некоторых источниках обозначается перечеркнутой буквой о), а r — радиус. Для измерения используют:
Диаметр состоит из 2 радиусов, а это значит, если необходимо узнать, чему равен радиус, необходимо длину диаметра разделить напополам. То есть разница между ними в 2 раза. Не всегда два радиуса образуют диаметр: только при условии, если они находятся на одной прямой.
Для решений задач можно использовать формулу: d =2*r. Естественно, формула работает в обратном направлении, она будет выглядеть следующим образом: r = d/2.
Дано: r =80 мм, определить, на сколько сантиметров диаметр длиннее. Для решения задачи используют формулу d=2*r. Но для начала необходимо перевести миллиметры в сантиметры. 80 мм=8 см. Далее d=2*8=16 см. Чтобы вычислить отличие, необходимо 16−8=8 см. Ответ — на 8 см длиннее.
Дополнительные сведения
Если в окружности провести 2 радиуса, то в результате круг будет разделен на 2 части, которые называются секторами. Отрезки образуют центральный угол.
Если в точке пересечения радиуса с поверхностью =начертить касательную, то обе линии будут перпендикулярными по отношению друг к другу. Если провести к хорде так, чтобы между ними образовался угол 90 0 , то в точке пересечения хорда будет разделена на 2 части. Если с хордой пересекается диаметр под углом 90 0 , то хорда и дуга будут разделены на две равные части.
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:
Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:
Построение окружности циркулем
Для построения окружности используют специальный прибор — циркуль:
Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:
Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.
Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:
Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:
Для обозначения дуг используется символ :
О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.
Хорда AB стягивает дуги AFB и AJB.
Радиус и диаметр окружности
Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружностиEсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.Формула радиуса окружности через диаметр:
Формула диаметра окружности через радиус:
Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.Существует радиус вписанной окружности
и радиус описанной окружности.Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.Как найти диаметр окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Читайте также:
- Как проверить очередь в детский сад кызыл
- Что такое пдо в детском саду
- Чем занимается комиссия по делам несовершеннолетних и защите их прав кратко
- Что такое штраф кратко
- В чем заключаются трудности эмпирической интерпретации понятий и утверждений теории кратко
Загрузить PDF
Загрузить PDF
Вычислить диаметр окружности не составит труда, если вы знаете какие-либо другие ее размеры: радиус, длину окружности или площадь ограничиваемого ею круга. Диаметр можно вычислить, даже не зная этих размеров – при наличии начерченной окружности. Если вы хотите узнать, как вычислить диаметр окружности, следуйте указанным ниже шагам.
-
1
Если вам известен радиус окружности, то, для того чтобы узнать диаметр, удвойте его. Радиус – это расстояние от центра окружности до любой точки, лежащей на ней. Например, если радиус окружности равен 4 см, то диаметр окружности составляет 4 см x 2, или 8 см.
-
2
Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π. Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.
-
3
Если вам известна площадь круга, то для нахождения диаметра разделите ее на π и извлеките из результата квадратный корень, чтобы получить радиус; затем умножьте на 2 для получения диаметра. Данное вычисление вытекает из формулы площади круга, A = πr2, преобразованной для нахождения диаметра. Например, если площадь круга равна 25 см2, разделите ее на число π и извлеките квадратный корень: √(25/3,14) = √7,96 = 2,82 см. Это радиус окружности. Умножьте его на 2, и вы получите диаметр: 2,82 х 2 = 5,64 см.
Реклама
-
1
Внутри окружности начертите горизонтальную прямую, проходящую от одной точки окружности к другой. Для этого воспользуйтесь линейкой или угольником. Прямая может проходить в верхней части круга, в нижней, или где-нибудь посередине.
-
2
Пометьте точки, в которых прямая пересекает окружность, буквами “A” и “B.”
-
3
Начертите две пересекающиеся окружности, одну – с центром в точке A, а другую – с центром в точке B. Убедитесь, что две окружности пересекаются так, будто образуют диаграмму Венна.
-
4
Через две точки, в которых окружности пересеклись, проведите прямую. Отрезок этой прямой между двумя точками и будет равен диаметру окружности.
-
5
Измерьте диаметр. Измерьте его с помощью линейки, а если нужна большая точность – штангенциркулем с цифровой индикацией. Готово!
Реклама
Советы
- Научитесь пользоваться циркулем. Это очень полезный инструмент, который предназначен для многих целей, включая определение диаметра окружности описанным выше графическим способом. Для этого можно также использовать измерительный циркуль.
- Работа с геометрическими формулами и уравнениями станет легче при условии постоянной практики. Попросите кого-то, кто работал с окружностями или другими геометрическими фигурами, помочь вам. Когда вы наберетесь немного опыта, вы скорее всего почувствуете, что задачи по геометрии будут казаться легче.
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Циркуль
- Линейка
- Штангенциркуль с цифровой индикацией (при необходимости)
Об этой статье
Эту страницу просматривали 1 261 507 раз.