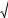
Кроме отмеченных, для таксации растущих деревьев вполне применимы упрощенные формулы Н.В. Третьякова и Б.А. Шустова:
|
V |
0,5795 d |
d d |
2 |
, |
V |
K d 2 |
q |
2 |
h, |
|
|
ств |
1 |
1 |
ств |
1,3 |
рассмотренные нами ранее в разделе по таксации срубленного ствола. Наконец, объем растущих стволов может вычисляться через их ви-
довые числа, найденные тем или иным способом:
|
V |
π |
d 2 |
H f . |
(4.13) |
|
|
ств |
4 |
1,3 |
|||
Возможно также использование таблиц объемов разнородной совокупности деревьев. Их обзор приводится в разделе 4.5.
Математические методы находят широкое применение в алгоритмах расчетов на ЭВМ при определении объемов растущих деревьев.
Изучению крон деревьев значительное внимание уделяется в курсах «Лесоведение» и «Биология». В курсе «Лесная авиация» установление формы и размеров крон древесных пород, их связей с таксационными показателями древостоев и условиями произрастания леса проводится для разработки дистанционных методов учета лесных ресурсов.
При лесоучетных работах также возникает необходимость таксации крон деревьев при решении задач, связанных с полным использованием всей биомассы лесных насаждений, определением прироста запаса и др. Такими показателями деревьев выступают диаметр, протяжение по стволу, объем и площадь поверхности кроны.
Диаметр кроны измеряют по замерам проекций на поверхность земли в направлениях север-юг и восток-запад, а ее площадь находят по формуле круга
|
S |
D2 |
. |
(4.14) |
|||
|
проекции |
||||||
|
4 |
кpoны |
|||||
На постоянных пробных площадях и таксационно-дешифровочных участках леса фактическую проекцию кроны определяют на плане пробы при помощи планиметра.
Протяжение кроны или длину кроны определяют как разницу между общей высотой ствола и высотой начала кроны в метрах. Оно может быть выражено и в процентах от общей высоты дерева.
Объем кроны можно найти по математическим формулам правильного тела вращения (параболоид, конус, шар) или же с помощью видовых чисел всего дерева или сучьев. Обычно применяют следующие простые формулы для хвойных и лиственных пород:
76

|
хвойные породы |
V |
D |
L |
; |
||
|
(с острой кроной) |
||||||
|
кроны |
кроны |
12 |
||||
|
лиственные породы |
V |
D |
L |
, |
(4.15) |
|
|
кроны |
кроны |
8 |
||||
где L – длина кроны;
Dкроны – диаметр кроны.
При вычислении приближенной площади поверхности крон деревьев используют формулу
|
S |
кроны |
D |
4 L2 D2 |
. |
(4.16) |
||||
|
4 |
кроны |
кроны |
|||||||
Для оценки морфологии насаждений часто применяют понятия: относительный диаметр кроны – Dкроны / Н ствола; степень развития кроны – Dкроны /L; сплюснутость кроны – L /Н ствола.
4.4.Определение возраста деревьев
Врезультате жизнедеятельности камбиальный слой дерева за каждый вегетационный период образует по периферии ствола годичное кольцо, состоящее из ранней и поздней древесины, различающихся по цвету древесины и структуре клеток. Одновременно из верхушечной почки ствола образуется годичный побег. Поэтому на продольном сечении ствол состоит как бы из множества конусообразных чехлов древесины, нанизанных друг на друга.
Возраст дерева определяют подсчетом числа годичных слоев на шейке корня. Однако на практике его чаще всего находят на пне срубленного дерева или возрастным буравом по кернам – на растущих деревьях на этой же высоте. При научных работах к указанному возрасту прибавляют число лет дерева, наросшего до высоты пня. Последнее зависит от породы, происхождения и условий местопроизрастания леса. Его устанавливают анализом в данном насаждении подроста аналогичной высоты.
У ряда лиственных пород (береза, осина, липа и др.) на срезах годичные слои мало заметны. В этих случаях древесину после соответствующей обработки поверхности смачивают водой, химикалиями и красящими веществами (чернила, марганцовка, хлористое железо и др.).
Для стоящих же деревьев возраст может быть определен лишь приближенно. Для этих целей используют свежие пни соседних срубленных деревьев, ведут подсчет мутовок деревьев сосны. Глазомерно возраст устанавливают по ряду совокупных внешних признаков дерева: d1,3
77
и h, форма кроны, очищенность нижней части ствола от сучьев, морфологическое строение кроны и др. Эти внешние признаки зависят от древесной породы, зонально-географических условий, типа леса, степени сомкнутости полога и т.п., что требует изучения и тщательной тренировки глазомера таксатора. Для примера сошлемся на исследования П.М. Верхуновым (1971) морфологических признаков возрастных поколений сосны в Сибири, внешних признаков возраста древостоев различных пород по А.Г. Мошкалеву и Г.М. Давидову (1992), деревьев лиственницы сибирской по В.И. Дитриху (1992) и др.
Выявление точного возраста даже для ряда срубленных деревьев связано с определенными трудностями, так как шейка корня обычно вдавливается в землю, на стволах появляется сердцевинная напенная гниль, наблюдаются случаи выпадения годичного кольца или образования ложных сдвоенных колец и т.п.
Помимо рассмотренного действительного возраста для деревьев с тем или иным периодом угнетения устанавливают хозяйственный возраст как число лет, в течение которых дерево при данных лесорастительных условиях и при нормальном росте достигло бы тех же размеров. Он определяется по формуле
|
A |
A |
Д |
, или A |
Д |
, |
(4.17) |
||||
|
хоз |
норм |
Д d |
хоз |
2 |
i |
|||||
где Анорм – число лет периода нормального роста дерева; Д – диаметр дерева в момент наблюдения;
d – диаметр угнетенной части дерева;
i – средняя ширина годичного слоя нормального роста дерева.
Учет хозяйственного возраста может иметь значение при таксации разновозрастных древостоев для правильного установления класса бонитета насаждения. Однако во всех случаях следует указывать и действительный возраст описываемых деревьев.
4.5. Таблицы объемов стволов разнородной совокупности деревьев
Таблицы объемов стволов представляют ряды числовых величин, расположенные в определенной системе и характеризующие средние объемы стволов отдельных древесных пород в зависимости от размеров и формы.
Первые таблицы объемов стволов были составлены в 1804 году Гартигом. Затем в 1846 году появляются более совершенные баварские таблицы. К настоящему времени лесотаксационная практика располагает большим множеством указанных нормативов, имеющих неодинако-
78
вую ценность. Достаточно подробно разработаны теория вопроса и методика составления этих таблиц.
Представляется возможным дать следующую классификацию существующих таблиц объемов стволов.
1. По целевому назначению различаются таблицы: а) для таксации разнородной совокупности деревьев; б) для таксации деревьев в древостоях.
2. По области применения существуют таблицы:
а) всеобщие или универсальные – для одновременной таксации стволов всех древесных пород;
б) общие – для данной породы в пределах ее ареала или страны; в) региональные – для данной породы в пределах выделенного лесо-
таксационного района.
3. По плану построения имеются таблицы:
а) с одним входом – d1,3;
б) с двумя входами – при средней форме по d1,3 и h (для таксации разнородной совокупности деревьев); при средней форме по d1,3 и разряду высот (для оценки деревьев древостоя). Для отдельных видов нормативов дополнительно могут учитываться некоторые лесобиологические признаки: возрастная группа, область роста, категории формы ствола и т.п.;
в) с тремя входами – коэффициент формы q2, d1,3 и h (для разнородной совокупности деревьев); разряд высот, средний q2 и d1,3 (для деревьев древостоя).
4.По методике сбора и группировке исходного материала таблицы объемов могут основываться:
а) на данных сплошной рубки или взятия учетных деревьев древостоя с отнесением всех стволов пробной площади к одному разряду вы-
сот и средних q2 составляемых таблиц;
б) на данных модельных деревьев, взятых в древостоях различных лесорастительных условиях, возраста, полноты, состава и т.п., с разноской отдельных стволов по принятым категориям учета.
5.По методике составления различают таблицы объемов:
а) с использованием средних значений видовых чисел по формуле
Vств = g1,3 ∙h∙f;
б) с графическим выравниванием объемов по d1,3 и h стволов;
в) с аналитическим выравниванием объемов по уравнениям связи от
d1,3, h и q2;
г) с математическим моделированием образующей ствола на ЭВМ.
79
Влитературе содержатся и иные классификации анализируемых таблиц.
К таблицам объемов растущих деревьев выдвигается требование обеспечить ту же точность определения запаса древесины, что и в таблицах учета заготовляемых из них круглых лесоматериалов.
Вразнородных совокупностях деревьев перечет ведется по группам
d1,3, h и q2. В древостоях элемента леса перечет проводится лишь по ступеням толщины с установлением общего разряда высот и среднего коэффициента формы стволов.
Рассмотрим отдельные наиболее известные таблицы объемов разнородной совокупности деревьев в их историческом плане.
Баварские таблицы объемов стволов. Они были опубликованы в
1846 году и для своего времени являлись наиболее совершенными. В дореволюционной России последние применялись с середины XIX века до 1886 года вплоть до появления русских временных массовых таблиц.
Воснову составления таблиц положены данные обмеров по коротким отрезкам 40220 стволов различных пород. Объемы стволов в них вычислены с использованием вырaвненных видовых чисел. Входами в таблицы являются диаметр на высоте 1,3 м с градацией в 2 см и высота ствола с дробностью в 0,5 м. Группировка материала проведена по возрастным категориям: для ели, пихты, сосны, лиственницы и бука – приспевающие (60…90 лет) и спелые (старше 91 года); березы – в возрасте 35…75 лет; дуба – около 150 лет.
Неоднократная опытная проверка баварских таблиц показала, что для отдельных деревьев погрешности могут достигать ± 15…20 %, а в партиях свыше 500 стволов не превышают ± 5 %.
Недостатками таблиц являются громоздкость и недостаточность числа наблюдений в отдельных учетных группах.
Германские таблицы объемов стволов. Были опубликованы в 1876
году и находят применение по настоящее время. В их основе лежат данные обмера свыше 64 тыс. деревьев сосны, ели, пихты, ольхи черной, дуба и бука.
По методике составления и результатам применения они близки к баварским таблицам. Нормативы предусматривают две области роста – северную и южную, а также возрастные группы деревьев до 40 лет, 41…80 лет и старше 80 лет. В них показаны объемы всего дерева и стволовой древесины толщиной свыше 7 см.
Новым в германских таблицах по сравнению с баварскими является использование для оценки формы стволов соотношения между диамет-
80
рами на середине высоты и на высоте 1,3 м, получившего впоследствии название второго коэффициента формы стволов.
Удельные таблицы Крюденера объемов стволов. В 1904 г.
А.А. Крюденером была опубликована программа работ, а в 1908-1913 гг. составлены таблицы объемов стволов для 9 древесных пород (сосна, ель, береза, осина, дуб, липа, граб, клен и ясень), предназначенные для таксации в лесах Удельного ведомства. Весь выпуск состоит из 20 отдельных книг.
В основе таблиц лежит обширный материал в виде обмера по 1,4 м отрубкам свыше 108 тыс. деревьев. Последние брались в качестве моделей в количестве 24…40 шт. на каждую пробную площадь. Некоторые же пробы были вырублены сплошь.
Построение таблиц отличается большой сложностью. В них в пределах породы последовательно необходимо различать входные признаки: область роста; тип дерева; тип насаждения; возрастную группу; высоту дерева; диаметр на высоте 1,3 м.
Однако этот план до конца не был выдержан. Так, области роста (северная и южная европейская части России) предусмотрены лишь по сосне и березе.
Типы деревьев (I, IIa, IIб, III) различаются по протяжению кроны на стволах и полнотах леса для учета полнодревесности стволов. Однако для деревьев III типа Крюденером таблицы составлены лишь по ели. По дубу и клену в один тип объединены деревья I и IIа категорий, а деревья IIб типа оставлены во II категории. По ясеню и грабу уже выделяются три формы деревьев по степени развития кроны, а по липе оставлены лишь две категории развитости кроны – стволы ровные и стволы, расходящиеся в сучья.
Типы насаждений также рассматриваются Крюденером по-разному. Так, по соснякам классификация дается по лесорастительным условиям леса; ельникам и березнякам – по средней высоте древостоя. В осинниках учитывается смешение пород, а в дубравах классификация дается по величинам коэффициентов формы q2. В нормативах по ясеню, грабу и липе тип насаждения уже совершенно не определяется.
Также запутанно учитывается в таблицах влияние возраста леса на объемы стволов. В сосняках по всем учетным категориям выделены группы возраста: приспевающие (60…95 лет), спелые (96…120 лет) и перестойные (121…150 лет). В ельниках только деревья I типа имеют разделение на группы возраста: 55…90 лет и 91…120 лет; для всех же остальных категорий таблицы едины. По остальным же породам возраст
81
деревьев как объемообразующий фактор в нормативах исключен полностью.
Таблицы Крюденера, по сути, являются переходными от оценки разнородной совокупности деревьев к таксации запаса отдельного древостоя. В них содержатся кроме объемов стволов данные абсолютного сбега, кубатуры сучьев и объемы бревен.
Достоинствами таблиц Крюденера являются:
а) попытка увязки выделения областей роста, типов леса и полноты древостоя с условиями произрастания древесных пород;
б) массовость наблюдений и сбор материала со сплошной рубкой стволов или значительного числа модельных деревьев на пробных площадях;
в) переход к учету формы стволов с помощью коэффициента формы q2, наличие таблиц сбега по каждой породе.
К недостаткам этих таблиц следует отнести следующие:
а) невыдержанность плана построения таблиц, приведшая к отказу от многих объемообразующих факторов;
б) разнообразие и множественность входов в таблицы; в) трудность пользования нормативами, неопределенность границ
областей роста; неувязанность возрастных групп с границами классов возраста.
Однако таблицы Крюденера не потеряли своей ценности до сих пор. Из-за богатства материала их используют как контрольные данные при изучении формы и размеров деревьев и при дальнейшей разработке теории вопроса. Таблицы были переведены в 1970 году проф. К.Е. Никитиным на ЭВМ в метрическую систему мер.
Индивидуализированные таблицы Шиффеля объемов стволов.
В период 1899-1908 гг. австрийский лесовод А. Шиффель составил таблицы объемов стволов для ели, сосны, лиственницы и пихты. Материалом для них послужили данные обмера 1 м отрубков около 5 тыс. деревьев. Стволы, взятые из разных древостоев, при обработке были распределены по высотам и пяти категориям значений q2 в зависимости от сомкнутости полога леса:
I – деревья свободного стояния с очень сбежистой формой ствола; II – редкие насаждения со значительной сбежистостью ствола;
III – насаждения средней сомкнутости со средней полнодревесностью ствола;
IV – полные сомкнутые насаждения с полнодревесной формой ствола;
82

V – очень густые насаждения с наиболее полнодревесными стволами.
По указанным группам полнот древостоев в таблицах были приняты средние значения коэффициентов форм q2, показанные в табл. 4.3.
Таблица 4.3 – Средние значения коэффициентов форм q2 в таблицах Шиффеля
|
Порода |
Средние значения q2 |
по группам сомкнутости полога леса |
||||
|
I |
II |
III |
IV |
V |
||
|
Лиственница |
0,50 |
0,58 |
0,62 |
0,72 |
0,76 |
|
|
Пихта |
0,52 |
0,58 |
0,62 |
0,68 |
0,72 |
|
|
Ель |
0,58 |
0,66 |
0,70 |
0,76 |
0,78 |
|
|
Сосна |
0,58 |
0,66 |
0,70 |
0,74 |
0,78 |
|
По каждой породе составлялись три таблицы:
а) видовых чисел и коэффициентов форм стволов в зависимости от высоты деревьев;
б) форм и объемов стволов по трем входам: высота дерева по первым ступеням; коэффициент формы q2 через 0,002; диаметр ствола через 2 см. В них показаны объемы ствола, крупной древесины и дерева, а также сокращенная характеристика абсолютного сбега стволов в виде диаметров на четвертях высот;
в) объемов ствола, дерева и крупной древесины в зависимости от h и
d1,3 деревьев.
Из-за сложности нахождения q2 на стоящих деревьях таблицы Шиффеля практического применения не получили. Однако они сохраняют свое теоретическое значение и используются в научных работах. Так, при составлении таблиц Союзлеспрома в 1931 году по сосне были использованы значения толщины кроны, указанные в анализируемых таблицах. Ряд методических приемов Шиффеля применяют при составлении современных таблиц объемов стволов.
По описываемой методике в 1908 году А.А. Маасом для лесов Швеции были составлены на основе обмера около 2 тыс. деревьев таблицы объемов стволов сосны и ели по разрядам q2 в 0,60; 0,65; 0,70; 0,75 и
0,80.
Для практического применения этих таблиц необходимо было замерить высоту ствола и диаметры растущих деревьев на высотах 1,3 м и 6,0 м. Допускалось для деревьев высотой до 21 м использование средней величины q2 = 0,70, а в других случаях q2 = 0,65.
Проф. В.К. Захаров (1961) для более широкого внедрения в производство нормативов Шиффеля и Мааса составил таблицу значений q2 стволов на основе измерений в натуре d1,3, d6,5 и h таксируемых деревьев.
83

Таблицы Шиффеля и Мааса имеют практически одинаковую точ-
ность ± 1,5…2 %.
Таблицы объемов Союзлеспрома для разнородной совокупности стволов. В 1931 году при составлении таблиц Союзлеспрома объемов стволов по бонитетам, предназначенных для таксации древостоев, исполнителями работ (по сосне – проф. Д.И. Товстолес; ели – проф. В.К. Захаров; осине и березе – проф. А.В. Тюрин) одновременно были разработаны таблицы объемов для разнородных совокупностей деревьев. Материалом для них послужили данные обмера около 12 тыс. модельных деревьев, проведенные при лесоустройстве. Объемы стволов определяли с помощью видовых чисел. Для каждой древесной породы предусмотрены (кроме осины) следующие три разряда значения коэффициентов формы q2 (табл. 4.4). В пределах этих разрядов q2 объемы стволов даются в зависимости от d1,3 и h.
Методика составления таблиц Союзлеспрома для оценки запаса древостоев излагается в разделе 8.5.
Таблица 4.4 – Средние значения коэффициентов форм q2 по разрядам
Средние значения q2 по разрядам объемных таблиц
Порода
|
1 |
2 |
3 |
|
|
Сосна |
0,59 |
0,65 |
0,71 |
|
Ель |
0,60 |
0,70 |
0,80 |
|
Дуб |
0,58 |
0,68 |
0,78 |
|
Береза |
0,57 |
0,66 |
0,75 |
|
Осина |
0,70 |
На практике таблицы объемов разнородных совокупностей деревьев иногда используют для оценки запаса древесины в древостоях по средним высотам ступеней и диаметрам деревьев.
В настоящее время на производстве получили широкое распространение региональные таблицы объемов стволов, составленные для разнородной совокупности деревьев различных пород. Они приводятся в лесотаксационных справочниках по отдельным районам страны, изданных в 1986-1993 гг. Федеральной службой лесного хозяйства России.
Универсальные таблицы для определения объемов стволов.
Впервые идея составления таблиц объемов стволов, единых для всех древесных пород, была высказана в 1926 году А. Самгиным и внедрена в производство в 1932 году А.Н. Карповым. Исходным положением послужил тезис о том, что независимо от древесной породы у стволов с одинаковыми диаметрами на высоте 1,3 м, высотами и коэффициентами формы q2 приблизительно одинаковы как диаметры на равных расстоя-
84
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
Часть измерения дерева – это измерение кроны дерево, состоящее из массы листвы и ветвей, растущих наружу из ствола дерева. Средний размах коронки – это средняя горизонтальная ширина коронки, взятая от капельной линии к капельной при ее движении вокруг коронки. Капельная линия является внешней границей участка, расположенного непосредственно под внешней окружностью ветвей дерева. Когда полог дерева намокает, вся лишняя вода сливается на землю по этой капельной линии. В некоторых списках также указан максимальный разброс коронки, который представляет собой наибольшую ширину от капельной линии до капельной линии поперек коронки. Другие измерения кроны, которые обычно проводятся, включают длину конечностей, объем кроны и густоту листвы. Картирование кроны обозначает положение и размер всех ветвей вплоть до определенного размера в кроне дерева и обычно используется при измерении общего объема древесины дерева.
Средний разброс кроны – один из параметров, обычно измеряемых в рамках различных программ деревьев чемпионов и документации. Другие часто используемые параметры, указанные в измерения дерева, включают высоту, обхват и объем. Дополнительные сведения о методологии измерения высоты дерева, измерения обхвата дерева и измерения объема дерева представлены по ссылкам в данном документе. Например, компания American Forests использует формулу для расчета баллов за большое дерево в рамках своей программы «Большое дерево», которая присуждает дереву 1 балл за каждый фут высоты, 1 балл за каждый дюйм обхвата и ⁄ 4 балл за каждую ногу распространения коронки. Дерево, набравшее наибольшее количество очков для данного вида, считается чемпионом в их реестре. Другой обычно измеряемый параметр, помимо информации о породе и местонахождении, – это объем древесины. Общий план измерений деревьев представлен в статье «Измерение деревьев», а более подробные инструкции по выполнению этих основных измерений приведены в «Руководстве по измерению деревьев Восточного общества коренных народов» Уилла Блоцана.
Содержание
- 1 Крупнейший зарегистрированные спреды кроны
- 2 Методики распространения кроны
- 2.1 Перекрестный метод
- 2.2 Среднее распространение кроны = (наибольшее распространение + наибольшее поперечное распространение) / 2
- 2.3 Метод спиц
- 2.4 Измерения в Google Планета Земля.
- 2.5 Метод многоугольников
- 2.6 Азимутальный метод
- 2.7 Максимальный размах кроны
- 3 Плотность кроны
- 4 Оценка объема кроны
- 4.1 Объем кроны живого дуба
- 5 Длина сгиба
- 5.1 Длина прямой линии снизу
- 6 Отображение кроны
- 7 См. Также
- 8 Ссылки
Наибольшие зарегистрированные размах кроны
Данные о наибольшем размахе кроны несколько ограничены, поскольку этот параметр не измеряется как часто, как высота дерева и обхват ствола. Самый крупный из зарегистрированных – «Монстр Монкира» (Eucalyptus microtheca ), расположенный у водоема Нейрагулли на юго-западе Квинсленда, Австралия, высота которого в 1954 году составляла 239 футов. В 1857 году Венесуэла имела ширину кроны 207 футов. Сообщается, что она все еще жива, но в плохом состоянии. Сайт Университета Коннектикута предполагает, что в дикой природе у них может быть размах кроны до 80 метров. Роберт Ван Пелт измерил распространение кроны дерева капок (Ceiba pentandra ) на острове Барро-Колорадо, Панама, в 2003 году, в 201 фут.
Методики распространения кроны
Cross -метод
Средний размах коронки – это среднее значение длины самого длинного разлета от края до края по всей коронке и самого длинного разлета, перпендикулярного первому поперечному сечению, через центральную массу коронки. Распространение кроны берется независимо от положения ствола. Размах следует измерять до кончиков конечностей, а не до «выемок» в форме макушки, и примерно под прямым углом друг к другу.
Средний размах кроны = (самый длинный размах + самый длинный поперечный размах) / 2
Геодезист определяет точку на земле непосредственно под кончиком ветви на одном конце измерений и отмечает это положение. Затем он переходит к противоположной стороне короны и находит точку под концом ветки. Разброс по этой линии – это горизонтальное расстояние между этими двумя позициями. На крутых склонах (более 15 градусов) расстояние между двумя точками можно скорректировать до истинного горизонта с помощью базовой тригонометрии. Горизонтальное расстояние = cos (наклон) × наклонное расстояние. Помощь помощника или использование лазерного дальномера могут значительно ускорить этот процесс. При использовании лазерного дальномера, как и при измерении высоты дерева, можно исследовать несколько точек на дальнем крае кроны, чтобы найти самую дальнюю точку. Лазерный дальномер также полезен для измерения ширины кроны там, где одна сторона кроны труднодоступна, например, дерево, растущее на скале или другом препятствии. Измерения с использованием лазерного дальномера, если они сделаны под большим углом, необходимо скорректировать на истинное горизонтальное расстояние, используя приведенную выше формулу.

Метод спицы
При использовании метода спицы четыре или более измерения выполняются от внешней капельной линии кроны до бокового края ствола. Расстояние до бокового края ствола практически равно расстоянию до центра ствола. Если измерение от капельной линии короны до бокового края ствола неровно, то измеренную длину необходимо преобразовать в горизонтальное расстояние.
- длина спицы = cos (наклон) × (измеренное расстояние)
Если угол наклона меньше 10 градусов, разница между горизонтальным расстоянием и измеренной длиной будет меньше 1,5% для наклонных расстояний менее 100 футов. Эти отдельные длины спиц усреднены, и это среднее значение равно половине среднего разлета коронки. Чем больше спиц измеряется в процессе, тем точнее определяется средний размах коронки.
- 2 ⋅ сумма n = средний разброс кроны { displaystyle 2 cdot { frac { text {sum}} {n}} = { text {средний разброс кроны}}}
Это предпочтительный метод исследователей полога и, вероятно, является наиболее точным, а также может использоваться для количественной оценки площади кроны. На больших деревьях это можно сделать быстро с помощью лазерного дальномера.
Еще один случай, когда полезны лазерный дальномер и клинометр, – это если кроны деревьев находятся высоко от земли. Например, белая сосна обычно имеет длинный голый стебель с ветвями, начинающимися высоко по стволу. В этих случаях для расчета длины спиц можно использовать серию снимков, сделанных по внешнему краю ветвей, стоящих сбоку от ствола. В этом случае углы будут крутыми, а длина спицы будет:
- cos (наклон) × (измеренное лазером расстояние) = длина спицы
измерения Google Earth.
С увеличением доступности аэрофотоснимков с высоким разрешением, доступных через Google Earth, можно различать кроны отдельных деревьев, что дает еще один вариант измерения распространения кроны. Широту и долготу дерева можно узнать прямо из Google Earth. Сама программа Google Планета Земля включает в себя линейку, которую можно использовать для измерения диаметров или спиц на кроне дерева. В качестве альтернативы можно измерить площадь коронки и рассчитать разброс коронки на основе этого значения. EasyAcreage V1.0 (демонстрационная версия) – это инструмент измерения площади Google Планета Земля, который вычисляет площадь любой формы, выделенной на экране Google Планета Земля. Обведите контур кронштейна деревьев, следуя ветвям и впадинам по периметру кроны, включая любые закрытые углубления в пределах контура кроны деревьев, и прочтите область, предоставленную Easy Acreage. Средний разброс короны можно определить с помощью простой формулы:
- разброс короны = 2 площади π { displaystyle { text {crown spread}} = 2 { sqrt { frac { text {area}} { pi} }}}
размах короны = 2 (площадь / π)
Здесь видно, что площадь – это площадь эквивалентного круга. Для критических измерений рекомендуется лично проверить измерения, сделанные с помощью приложения дистанционного зондирования.
Leverett также предоставил четыре варианта измерения площади коронки с помощью компаса и клинометра по внешнему краю коронки или путем комбинации измерений от края коронки до туловища и вокруг периметр кроны. Все четыре очерчивают капельницу области короны многоугольником и делят многоугольник на ряд смежных треугольников, измеряют площадь каждого треугольника и просуммируют их. Один из вариантов, полигональный метод, измеряет каждую сторону треугольника для вычисления его площади. Второй и третий методы используют азимуты и одно расстояние до ствола для расчета площади. Четвертый метод, метод азимута, требует только азимутов и измерений расстояния от точки к точке по периметру короны.
Метод многоугольника
Измеритель проходит по периметру коронки довольно близко по капельной линии. На земле отмечаются точки, которые представляют собой контур короны, и отмечаются таким образом, чтобы следующая точка всегда была видна по сравнению с предыдущей. Для первой точки расстояние до центра ствола дерева измеряется вместе с вертикальным углом к точке. Затем вместе с вертикальным углом измеряется расстояние до следующей внешней точки. Измеритель перемещается к следующей внешней точке и повторяет процесс, продолжая по часовой стрелке, пока корона не будет окружена. Последний отрезок первого треугольника становится первым отрезком второго треугольника и так далее, поэтому только первый треугольник требует измерений для всех трех отрезков. В результате получается серия смежных треугольников с определенными сторонами. Площадь каждого треугольника вычисляется по его сторонам и вычисляется сумма площадей. Каждый треугольник покрывает часть области короны. Сумма треугольников равна общей предполагаемой площади кроны. Необходимые инструменты включают лазерный дальномер или рулетку и клинометр.
Метод азимута
В четвертом методе измеритель не взаимодействует с стволом или какой-либо внутренней точкой многоугольника. Измеритель проходит по периметру, снимая горизонтальные расстояния и азимут до следующей точки, пока периметр короны не будет обведен кружком. Это самый простой и гибкий метод из четырех. Этот метод также можно легко использовать для измерения площади других встречающихся объектов, например, групп деревьев или весенних водоемов.
Максимальный разброс кроны
Это еще одно измерение, которое иногда собирают. Максимальный размах кроны – это максимальная ширина кроны вдоль любой оси от капельной линии на одной стороне дерева до капельной линии на противоположной стороне дерева.
Плотность кроны
Лесная служба Министерства сельского хозяйства США опубликовала руководство по полевым оценкам различных характеристик кроны, выходящим за рамки обычных базовых измерений. Включен ряд определений терминов, формы кроны, плотности кроны / прозрачности листвы, соотношения живой неуплотненной кроны, класса силы и различных оценок усыхания.
Плотность кроны – это количество ветвей кроны, листвы и репродуктивных структур, которые блокируют видимость света через крону. У каждого вида деревьев есть нормальная крона, которая меняется в зависимости от участка, генетики, повреждения дерева и т. Д. Она также служит индикатором ожидаемого роста в ближайшем будущем. Плотность кроны можно оценить с помощью карты Crown Density-Foliage Transparency Card. Используя карту для справки, наблюдатель оценивает, какой процент света блокируется массой короны. Оценки производятся с двух разных направлений под прямым углом и согласовываются для определения плотности кроны. Также существуют различные электронные плотномеры, которые измеряют плотность кроны или листвы.
Оценка объема кроны
Объем кроны включает весь живой полог дерева от основания живой кроны до верхнего края кроны и от внешнего края ветки кончиками внутрь. Он не включает мертвые ветви выше или ниже живой части полога, а также какие-либо эпикормальные побеги ниже основания живой кроны. Он действительно включает пустоты или пустоты, заключенные в этих границах. Объем кроны действительно измеряет массу ветвей или листвы, поскольку он не включает измерения плотности листвы и ветвей, а не их вес. Объемы короны обычно не могут быть адекватно представлены простыми геометрическими фигурами из-за их неправильной формы.
Для чрезвычайно сложных форм поверхность коронки может быть нанесена на карту в трех измерениях с помощью ряда внешних или внутренних съемочных станций. С каждой станции положение точки на поверхности короны может быть нанесено на карту с помощью компаса, лазерного дальномера и клинометра. Выполненные измерения включают азимут от места съемки, расстояние от места съемки, расстояние до точки и наклон к точке. Их можно преобразовать в координаты (x, y, z) для каждой точки, а измерения между разными точками съемки можно связать вместе, измеряя относительные положения между разными точками съемки.
Расстояние до целевой точки:
- cos (наклон) × лазерное расстояние = (горизонтальное расстояние)
Положение точки относительно позиции с использованием магнитного севера:
- y- axis = (расстояние по горизонтали) × cos (азимут)
- ось x = (расстояние по горизонтали) × sin (азимут)
Высота точки относительно положения измерения составляет:
- z- ось = sin (наклон) × расстояние, измеренное лазером = высота
Необходимо провести достаточные измерения для создания трехмерного графика поверхности внешнего края купола. Затем объем можно разбить на более мелкие срезы, рассчитать объем каждого отдельного среза и сложить объем всех срезов, чтобы определить общий объем навеса.
Объемы кроны живого дуба
Короны большинства деревьев слишком неправильной формы, чтобы их можно было смоделировать простой геометрической фигурой. Исключением могут быть неглубокие куполообразные кроны живых деревьев дуба (Quercus virginiana) на юге и юго-востоке США. Хорошее описание общей формы можно сравнить с обнаженной частью полусферы, частично зарытой в землю. Была разработана модель, по которой можно определять объем кронштейнов деревьев такой формы. Крона дерева соответствует этой модели формы, если:
- a) она имеет куполообразную верхнюю поверхность,
- b) основание кроны является плоским или находится на уровне земли на плоской поверхности, и
- в) ширина кроны больше или равна удвоенной вертикальной толщине кроны.
Многие из живых дубов не имеют идеально круглого отпечатка кроны. Одна ось дерева будет шире перпендикулярной оси. Если эти значения относительно близки, просто усредните две оси, чтобы получить средний размах кроны. Если они сильно различаются, то длины оси могут быть преобразованы в эквивалентный круговой радиус для использования при расчете объема короны по следующей формуле:
- малая ось радиуса × большая ось радиуса { displaystyle { sqrt {{ text {radius}} _ { text {minor axis}} times { text {radius}} _ { text {major axis}}}}}
Это небольшое исправление. Для выполнения расчетов объема была разработана электронная таблица Excel.
Метод поворота профиля. Объем коронки можно определить с помощью трех значений:
- размах коронки,
- толщина коронки,
- форма коронки.
Толщина коронки и средний размер коронки будут быть измеренным, и общая форма кроны дерева будет определена путем визуального сравнения с диаграммой. Форма кроны будет использоваться для получения значения формы кроны (CF) для различных форм деревьев и будет третьим параметром формулы расчета объема кроны. Крона дерева может быть разделена на 10 дисков, каждый из которых составляет 1/10 высоты кроны. Диаметр каждого диска может быть выражен как некоторая часть среднего размаха коронки. Независимо от того, выше ли дерево и каждый диск представляет большую длину кроны, или если размах кроны больше или меньше, каждый диск будет представлять одну и ту же долю от общего объема кроны. Учтите, что должен быть один цилиндр той же высоты, что и толщина коронки, который имеет тот же объем, что и коронка неправильной формы. Тогда проблема состоит в том, чтобы определить диаметр этого цилиндра, чтобы его объем был равен объему кроны дерева. Объем каждого отдельного диска можно рассчитать по формуле для объема цилиндра:
- объем диска = π ⋅ высота ⋅ радиус 2 = π ⋅ высота ⋅ (диаметр 2) 4 { displaystyle { text {объем диска}} = pi cdot { text {height}} cdot { text {radius}} ^ {2} = pi cdot { frac {{ text {height}} cdot ({ text {диаметр}} ^ {2})} {4}}}
Переставляя числа, можно получить формулу для радиуса, необходимого для решения с одним цилиндром. Высота и π выпадают, и в результате получается необходимый радиус, равный квадратному корню из среднего квадрата радиуса для каждого из дисков.
- радиус цилиндра = средний (r 2) { displaystyle { text {radius}} _ { text {cyl}} = { sqrt { operatorname {average} (r ^ {2})}}}
Профили формы дерева могут быть рассчитаны индивидуально для каждого встречающегося дерева. Однако при изучении профилей большого количества деревьев разных видов было обнаружено, что типичные профили варьируются в соответствии с закономерностью, и для каждого семейства профилей существует значение формы кроны, которое можно использовать для расчета объема кроны. Каждая различная форма короны будет иметь соответствующее отношение формы короны измеренного максимального среднего разброса короны к радиусу эквивалентного диаметра цилиндра. Это значение нельзя использовать напрямую, но сначала необходимо преобразовать в уникальное значение коэффициента формы короны.
Формула для эквивалентного цилиндра может быть выражена следующим образом:
- объем короны = объем эквивалентного цилиндра = π hr 2 = π ⋅ (толщина короны) × коэффициент формы коронки × средний минимальный размах коронки 4 где средний минимальный разброс короны = 2 × средний максимальный радиус { displaystyle { begin {align} { text {объем короны}} = { text {объем эквивалентного цилиндра}} = pi hr ^ {2} \ [5pt] = {} pi cdot { frac {({ text {толщина короны}}) times { sqrt {{ text {соотношение формы короны}} times { text {средняя минимальная коронка spread}}}}} {4}} \ [5pt] { text {где средний минимальный разброс короны}} = 2 times { text {средний максимальный радиус}} end {выровнен}}}
Константы можно изменить, чтобы получить коэффициент формы короны (CF):
- CF = π ⋅ (коэффициент формы короны) 2 4 { displaystyle { text {CF}} = { frac { pi cdot ({ text {соотношение формы коронки}}) ^ {2}} {4}}}
Уравнение общего объема можно переписать следующим образом:
- объем коронки = (CF) × (толщина коронки) × (средняя минимальный размах короны) 2 { displa ystyle { text {объем короны}} = ({ text {CF}}) times ({ text {толщина короны}}) times { big (} { text {средний минимальный разброс короны}}) ^ {2}}
Таким образом, сложная задача оценки объема коронки сводится к двум легко измеряемым параметрам – среднему максимальному размаху коронки и толщине коронки и одному значению, которое можно определить с помощью визуального сопоставления форм из таблицы стандартных форм. Открытые области, содержащиеся в объеме вращения, считаются частью объема кроны, в то время как случайные кончики ветвей, выходящие за пределы объема вращения, исключаются. У некоторых деревьев просто форма кроны слишком неправильная, чтобы использовать эту методику для определения объема кроны. Эти деревья, если требуется значение объема кроны, необходимо будет оценить по секциям, а объем каждой секции рассчитать индивидуально.
Длина конечности
Самая длинная конечность измеряется от воротника, где она выходит из туловища, до самой дальней горизонтальной протяженности. Также следует отметить, является ли конечность самонесущей или касается ли она земли где-то по своей длине. Длину конечности также можно измерить по контуру самой конечности. Если это легко сделать, это можно сделать с помощью рулетки. Если конечность недоступна, необходимо использовать дистанционные методы измерения. Существует несколько эффективных методов измерения, которые могут предоставить нам полезную информацию о разгибании конечностей.
Длина прямой линии снизу
Длину конечности можно измерить с помощью лазерного дальномера и клинометра, если оба конечные точки конечности видны из точки под концом конечности. Расстояние по вертикали измеряется до конца отгиба непосредственно над точкой измерения под углом 90 градусов. Затем измеряют наклон и расстояние до другого конца конечности, где она выходит из туловища. Затем можно рассчитать длину прямой линии конечности от туловища до кончика с помощью закона косинусов.
Для длинных конечностей с изменяющейся кривизной почти всегда требуется определение длины конечности на более мелкие сегменты, при этом каждый сегмент измеряется независимо. если должна быть достигнута приемлемая точность. Длину можно рассчитать на основе модели двумерной криволинейной регрессии с использованием нескольких точек измерения. Это многообещающе при условии, что используется программа регрессии, которая допускает как двумерную линейную, так и нелинейную регрессию. Хорошим статистическим пакетом, который обеспечивает эту возможность, является Minitab, который поддерживает уравнения второй и третьей степени. Модели регрессии для парабол и форм экспоненциальной кривой были разработаны NTS в формате электронной таблицы Excel для тех, кто не использует статистическое программное обеспечение. Особый интерес представляет параболическая кривая. Табличное приложение этого для параболических кривых было разработано NTS. Таблица соответствует параболе до 4 или более точек (до 10 допустимых) с использованием метода наименьших квадратов, а затем вычисляет длину (длины) конечностей с использованием правила Симпсона для вычисления определенного интеграла.
Длина конечности с помощью внешней ссылки Позиция. Наземные измерения могут использоваться для дистанционного измерения длины конечностей и диаметров ответвлений с помощью монокуляра с сеткой или фотографического анализа. Длину сегмента можно определить путем измерения положения конечных точек ответвления в трехмерном пространстве от внешней исходной позиции. Затем длина рассчитывается с применением теоремы Пифагора. Следующая диаграмма иллюстрирует этот процесс.

От внешней исходной позиции O прямое расстояние до L 1 измеряется до P 1 вместе с вертикальным углом V 1 и азимут A 1. Затем вычисляются координаты x 1, y 1 и z 1. Же процесс следует при Р 2.
Эта последовательность осуществляется следующим образом:
Горизонтальное расстояние d 1 от начальной точки отсчета O к целевой точке Р 1 вычисляется как d 1 = cos (наклон) × лазерное расстояние = L 1 sin V 1 Значение x в первой точке: x 1 = sin (азимут) × горизонтальное расстояние = d 1 sin A 1 Значение y в первой точке: y 1 = cos (азимут) × расстояние по горизонтали = d 1 cos A 1 Значение z в первой точке: z 1 = sin (наклон) × лазерное расстояние = L 1 sin V 1 Этот процесс повторяется для P 2, чтобы получить (x 2, y 2, z 2) Последний шаг – вычислить расстояние от P 1 до P 2 (L) по следующей формуле.
- L = (x 2 – x 1) 2 + (y 2 – y 1) 2 + (z 2 – z 1) 2 { displaystyle L = { sqrt {(x_ {2} -x_ {1})) ^ {2} + (y_ {2} -y_ {1}) ^ {2} + (z_ {2} -z_ {1}) ^ {2}}}}
Обратите внимание, что мы возводим изменения в квадрат. в значениях x, y и z, складывая эти квадраты вместе и извлекая квадратный корень из суммы.
Леверетт разработал методику, при которой длина конечности измеряется с помощью монокуляра с сеткой, выровненной вдоль ориентация конечности, расстояние до обоих концов сегмента конечности и вычисленный коэффициент масштабирования для определения длины конечности. По сути, видимая длина конечности на каждом конце с использованием расстояния до этой точки и масштабного коэффициента для этого расстояния, как если бы конечность была перпендикулярна наблюдателю. Эти длины считаются вершиной и основанием правильной трапеции с высотой, равной разнице расстояний между двумя точками. Затем можно вычислить истинную длину конечности, рассматривая ее как диагональ трапеции.
Отображение навеса
Отображение навеса – это процесс, посредством которого положения и размер ветвей внутри навеса отображаются в трехмерном пространстве. Это трудоемкий процесс, который обычно применяется только для наиболее значимых образцов. Обычно это делается из заданной позиции или ряда позиций в дереве. Эскизы и фотографии используются для облегчения процесса. По деревьям взбираются и отображается общая архитектура, включая расположение главного ствола и всех повторяющихся стволов, в дополнение ко всем ветвям, исходящим от стволов. Также отображается положение каждой точки ветвления в кроне до определенного размера, а также положения различных повторов, изломов, перегибов или любых других эксцентриситетов на дереве. Каждый нанесенный на карту ствол и ветвь измеряются по базальному диаметру, длине, азимуту, альпинисты измеряют определенные окружности и детализируют другие особенности дерева.
См. Также
Портал деревьев
- Закрытие короны
- Классы короны
- правило ветвления да Винчи
- Диаметр на высоте груди
- Лесной инвентарь
Ссылки
Содержание
- Таксация растущего дерева
- Диаметр кроны деревьев
- ОБЩИЕ СВЕДЕНИЯ О ДЕРЕВЬЯХ И КУСТАРНИКАХ, ИХ РОСТЕ И ДОЛГОВЕЧНОСТИ
- ПОСМОТРЕТЬ ЕЩЕ:
Таксация растущего дерева
У растущего дерева чаще всего определяют диаметр ствола на 1,3 м, высоту, объем ствола и возраст. Иногда определяют диаметр и длину кроны.
Диаметр у дерева измеряется обычно на высоте 1,3 м от шейки корня, т.е. на высоте груди человека среднего роста. Поэтому в лесной таксации такой диаметр называют диаметром на высоте груди. С использованием этого диаметра составлено множество таксационных таблиц – видовых чисел, объемов стволов, хода роста, сортиментных, товарных.
Для измерения диаметра ствола на высоте груди применяют разные инструменты и методы. Одним из простых инструментов, находящих самое широкое применение в практике лесного хозяйства, является мерная вилка.
Мерная вилка служит для измерения диаметров стволов у деревьев. С ее помощью также можно измерить высоту деревьев. Мерная вилка (рис.1) представляет собой большой (длиной от 0,7 до 1,2 м) штангельциркуль, изготовленный из дерева, текстолита или дюралюминия. Она состоит из линейки-штанги 1, с делениями в сантиметрах (с одной стороны разбитых до 0,5 см), пронумерованных через 2 или 4 см, на одном конце которой закреплена неподвижная ножка 2. Подвижная ножка 3 надета на линейке- штанге и перемещается по ней при измерении диаметров стволов. При измерениях вилка прикладывается к стволу так, чтобы спереди прикасалась линейкой-штангой, а с боков – неподвижной и подвижной ножками, т.е. с трех сторон.
Рисунок 1. Общий вид мерной вилки:
1 ─ измерительная линейка-штанга,2 ─ неподвижная ножка, 3 ─ подвижная ножка
Рулетка или тесемочный метр. С их помощью также можно измерять диаметр ствола, производя замеры его окружности L. Для получения диаметра (Д) необходимо применить формулу:
Высоту ствола измеряют с точностью 1 м или 0,5 м. Низкие деревья можно измерять с более высокой точностью. Для этого используются специальные высотомеры, а также другие инструменты и способы
Высотомер представляет собой небольшой (массой до 100-150 г) прибор, предназначенный для измерения высот растущих или сухостойных деревьев. Высотомеры выпускаются различных марок: ВУЛ-1, ВН, ВКН, ВА. Довольно широко используются зарубежные высотомеры: СУУНТО (Финляндия), Блюме-Лейсс (ФРГ), оптический цифровой (Швеция) и др.
Большинство высотомеров механического действия имеют барабан, снабженный балансиром, со шкалами высот при базисах 15 или 20 м. Балансир обеспечивает постоянное положение шкал к линии горизонта. Тормозное устройство барабана выполнено в виде кнопки, с помощью которой барабан удерживается при визировании высотомера на вершинку (верхнюю точку) дерева.
Высотомер для измерения высот деревьев можно на время взять в лесничестве.
Чтобы измерить высоту дерева, необходимо отмерить базис (расстояние от дерева) 15 или 20 м. Базис должен быть равен примерно высоте дерева. С этой точки и производится измерение высоты. Нажав на кнопку прибора, сначала нужно произвести визирование через окуляр на верхнюю точку дерева. Кнопку отпустить и по шкале снять отсчет. К полученному значению необходимо в равнинных условиях добавить высоту мерщика от земли до уровня глаз. При измерении высоты дерева в горной местности лучше произвести визирование дважды — на его вершину и основание (шейку корня). Если отсчеты на шкале окажутся по разные стороны от «0», то результат суммируется, а если по одну сторону от «0» — вычитаются.
Высоту дерева можно также измерить с помощью мерной вилки (ее также можно взять в лесничестве), если у нее на конце неподвижной ножки прикреплена нить длиной около 40см с отвесом, а на подвижной ножке имеется шкала с делениями, обозначающими высоту.
При измерении также необходимо отмерить базис, равный примерно высоте данного дерева. Став с мерной вилкой на полученную точку, подвижную ножку установить на линейке – штанге на деление, численно равное базису, и по внутренней грани неподвижной ножки произвести визирование на верхнюю точку измеряемого дерева. Нить с отвесом на шкале боковой части подвижной ножки покажет значение высоты дерева от уровня глаз мерщика (рис.2). Для получения высоты дерева от шейки корня необходимо добавить к полученному результату высоту до уровня глаз человека.
Рисунок 2. Измерение высоты дерева с помощью мерной вилки: а − общий вид, б − положение мерной вилки при визировании на вершину дерева
Измерение высоты дерева по падающей тени. Измерение высоты по тени следует проводить в солнечную погоду у стоящих одиночно деревьев. Сначала следует измерить длину падающей тени от дерева. Затем взять палочку длиной 1-2 м, воткнуть ее в землю вертикально и замерить тень, которую она отбросит (рис. 3). Высота дерева будет равна:
Н = 
где: Н – высота дерева, м,
h — высота вешки (палочки), м,
L – длина падающей тени от дерева, м,
l – длина падающей тени от вешки, м.
Рисунок 3.К измерению высоты дерева по падающей от него тени
Измерение высоты дерева с использованием равнобедренного треугольника. Для этого необходимо вооружиться указанным треугольником (с наличием прямого угла), а также рулеткой.
Вначале на дереве следует отметить высоту на уровне глаз мерщика.
Затем отойти от дерева на расстояние, равное примерно его высоте.
Приставив угольник одним из острых углов (45 0 ) к глазу, прилегающим катетом произвести визирование на отметку уровня глаз исполнителя на дереве. Далее необходимо визировать по длинной стороне треугольника, отходя от дерева или приближаясь к нему, чтобы линия визирования точно указала на верхнюю точку дерева (рис.4а). От места стояния (точки) измерить расстояние до дерева. Прибавить к полученному значению отрезок, равный высоте исполнителя до уровня глаз. Это и будет высота дерева.
Рисунок 4. К определению высоты дерева с использованием равнобедреннего треугольника с углами 45 0 (а) и крестообразно соединенных палочек (б)
В лесных условиях равнобедренный треугольник можно получить, взяв две одинаковые палочки длиной 25- 30 см. В одной из палочек посредине сделать, чтобы просунуть в нее вторую палочку. Палочки выравнять по длине и прямым углам. Мысленная прямая, соединяющая два конца от горизонтальной к вертикальной палочкам, будет гипотенузой, которую следует визировать на вершину дерева (рис.4б).
Определение высоты дерева по отметке его относительной высоты. На плоской палочке длиной до 30 см (можно использовать для этого обычную ученическую линейку) можно отграничить двумя линиями отрезок 20-25 см. Кроме того, нанести границу 0,1 длины отрезка. Отойти от дерева на расстояние, примерно равное его высоте, держа палочку (линейку) вертикально, отставить ее от глаза наблюдателя так, чтобы дерево по высоте точно вписалось в границы, отмеченные на палочке (рис. 5). При этом риска 0,1 должна быть в нижней части вертикально расположенной своеобразной шкалы. Далее замечается на дереве точка, которая получается визированием через риску 0,1. Задача отметки этой точки облегчится, если у мерщика будет помощник. Остается измерить высоту дерева от шейки корня до данной точки и полученную величину увеличить в 10 раз.
Рисунок 5. К определению высоты дерева по отметке 0,1 его относительной высоты
Объем ствола V растущего дерева можно вычислить по достаточно простым формулам:

где Д – диаметр на 1,3 м, см
где: Д – диаметр на 1,3 м, м,
Н — высота ствола, м .
Например, диаметр Д у дерева равен 28 см, высота Н – 25,9 м. Объем ствола по первой формуле будет равен: V = 0,001 Д 2 = 0,001∙28 2 = 0,784 м 3 , по второй — V = Д 2 ∙ Н / 3 = 28 2 ∙ 25,9 / 3 = 0,677 м 3 .
Возраст растущего дерева определяют по годичным кольцам на кернах, полученных возрастным буравом. Сверление производят примерно на уровне пня. У молодых сосен возраст можно определить по «мутовкам» — местам прикрепления боковых веток к центральному побегу (в последующем стволу).
Возрастной бурав (рис.6)позволяет взять керн у растущего дерева. Керн представляет образец древесины диаметром от 4,3 до 5,15 (иногда до 10) мм, по форме напоминающий круглый (без граней) карандаш. Буравы выпускаются длиной 10-50 см (с градацией 5см) и 60-80 см (с градацией 10 см). Состоит бурав из собственно бурава – трубки, на конце которой находится режущая головка, которая позволяет ввинчивать трубку в древесину; футляра- воротка, представляющего собой также пустотелую трубку, но большего диаметра. В собранном виде он выполняет роль футляра, а при бурении – рукоятки. В средней части футляра сбоку находится четырехгранное окно, в которое при бурении вставляется второй конец бурава. В комплект также входит желобковая лопаточка (экстрактор) для извлечения керна из полости бурава (см. рис.6).
Рисунок 6. Возрастной бурав:
1 − бурав, 2 − футляр-вороток, 3 − экстрактор, 4 − защелка
Источник
Диаметр кроны деревьев
Важнейшими характеристиками, которые учитываются при использовании деревьев и кустарников в озеленении, являются их размеры. В табл.1 приводится условная классификация наиболее распространенных деревьев и кустарников по высоте во взрослом состоянии. Все деревья и кустарники относятся к трем классам по высоте:
1 класс – от 20 м и выше 1 класс – от 3 м и выше
11 класс – от 10 м до 20 м 11 класс – от 1 м до 3 м
111 класс – до 10 м 111 класс – до 1 м
Обычно деревья первой величины имеют широкую (более 10 м в диаметре) крону – дуб, клен остролистный, ясень.
Крону средних размеров (диаметром 5-10 м) имеют деревья второй величины – груша обыкновенная, клен полевой.
Таблица 1. Классификация деревьев и кустарников по высоте
| Класс высоты | Высота, м | Хвойные | Лиственные |
| Деревья первой величины | 20 и более | Ель обыкновен. ель колючая, лиственница европейская, л. сибирская, пихта сибирская, сосна Веймутова, сосна кедровая сибирская, с.обыкновенная | Береза бородавчатая, б.пушистая, вяз гладкий, обыкновенный, вяз шершавый, дуб черешчатый, дуб красный, ива белая, каштан конский, клен остролистный, липа крупнолистная, л. мелколистная, орех маньчжурский, осина (тополь дрожащий), тополь белый, т.берлинский, т.душистый, т. черный, ясень обыкновенный |
| Деревья второй величины | 10-20 | Можжевельник виргинский, мож. казацкий, тис ягодный, туя западная. Можжевельник высокий, сосна румелийская, с.горная, | Груша обыкновенная, акация белая, ива ломкая, клен полевой, клен ясенелистный, шелковица белая |
| Деревья третьей величины | до 10 | кедровый стланец, можжевельник обыкновенный | Рябина обыкновенная, черемуха обыкновенная, черемуха виргинская, вишня обыкновенная, груша уссурийская, клен татарский, к. гиннала, яблоня сибирская (ягодная) |
| Кустарники высокие | 3 м и более | Сосна горная низкорослая, кипарисовик горохоплодный, можжевельник средний, м. виргинский, туи низкорослые | Акация желтая, бересклет европейский, боярышник обыкновенный, б. сибирский, бузина красная, гортензия метельчатая, жимолость татарская, ирга обыкновенная, калина обыкновенная, лещина обыкновенная, ракитник «Золотой дождь», роза краснолистная, сирень венгерская, с. обыкновенная, снежноягодник кистевой, спирея калинолистная, спирея средняя, чубушник венечный |
| Кустарники средней высоты | 1-3 | Кипарисовик Лосона, можжевельник горизонтальный, м. казацкий, м.обыкновенный, туя западная | Айва японская, барбарис обыкновенный, дерен белый сибирский, жимолость синяя, жимолость съедобная, кизильник блестящий, лох серебристый, малина душистая, роза коричная, р. морщинистая, смородина золотистая, смородина черная, красная, спирея иволистная, с. острозубчатая, с. рябинолистная, с. Ван-Гутта |
| Кустарники низкие | до 1 | Барбарис Тунберга, дафна (волчеягодник) обыкновенная, дейция изящная, дрок красильный, кизильник горизонтальный, миндаль низкий, роза миниатюрная, спирея Бумальда, с. японская |
Узкую крону (диаметром 2-5 м) имеют деревья третьей величины – рябина обыкновенная, черемуха обыкновенная, яблоня ягодная.
У кустарников обычно диаметр кроны имеет следующие размеры: у высоких – 3-5 м, у кустарников средней высоты – 1-3 м, у низких – 0,5-1 м.
Быстрота роста
Важным свойством древесных растений является быстрота роста. Прирост древесных растений определяется по трем критериям: высота, ширина (диаметр кроны), толщина (диаметр ствола).
Быстрота роста деревьев в высоту определяется размером ежегодного прироста высоты стебля. Для практических целей паркостроительства обычно принимают во внимание прирост древесных пород в высоту (табл.2)
Таблица 2. Классификация деревьев и кустарников по быстроте роста в высоту
| Ежегодный при-рост | Класс быстроты роста в высоту | Хвойные | Лиственные |
| До 2 м и более До 1 м До 0,5-0,6м До 0,25-0,3 До 0,15 м и менее | Весьма быстро- расту- щие: деревья: кустар- ники: Быстро-расту-щие: деревья: кустар-ники: Умерен-ного роста: деревья: кустар-ники: Медлен-норас-тущие: деревья: кустар- ники: Весьма медлен-норас-тущие: деревья: кустар-ники: | Лиственница евро-пейская, л. сибир-ская, сосна обыкновенная, с. Веймутова, ель обыкновенная Пихта сибирская, ель колючая, можжевельник виргинский, туя западная Сосна горная низ-корослая Сосна сибирская кедровая Можжевельник казацкий, м. обык-новенный Кедровый стланец, тис ягодный, карликовые формы хвойных пород Все карликовые кустарниковые формы хвойных древесных пород | Тополь бальзамический, т. канадский, т. черный, осина, ива белая, береза бородавчатая, клен ясенелистный Акация желтая, бузина черная, б. красная, чубушники, дейция городчатая, форзиция, спирея калинолистная, с. рябинолистная, с. Ван-Гутта Вяз шершавый, в. мелколистный, дуб красный,ясень обыкновенный Бересклет европейский, дерен сибирский, жимолость татарская, калина обыкновенная, лещина обыкновенная, ракитник «золотой дождь», смородина золотистая Дуб черешчатый, клен остролистный, к. полевой, липа крупнолистная, л. мелколистная, Айва японская, клен гиннала, сирень обыкновенная Груша лесная, яблоня сибирская Боярышник обыкновенный, ирга обыкновенная, облепиха Карликовые формы лиственных пород Волчеягодник обыкновенный, все карликовые формы лиственных пород |
Прирост кроны в ширину у древесных пород, как правило, отстает от прироста в высоту, но продолжается даже после прекращения прироста в высоту.
Таблица 3. Высота основных видов древесных растений, м
| Породы | Возраст древесных растений, лет | |||||
| Весьма быстрорастущ.: Тополь канадский Т. берлинский Т. черный Береза бородавчат. | 2,5 | 13,5 | 28,5 | |||
| Быстрорастущие Лиственные: Ясень обыкновен. Вяз мелколистн. Дуб красный Хвойные деревья: Лиственница евр. Л.сибирская Сосна Веймутова С. обыкновенная Ель обыкновенная Умеренного роста Лиственные: Клен остролистн. Дуб черешчатый Вяз гладкий Липа крупнолистн. Л. мелколистная Хвойные деревья: Пихта сибирская Ель колючая Медленнорастущ. Лиственные: Груша обыкновен. Яблоня ягодная Хвойные деревья: Сосна сибирская Туя западная Весьма медленнорастущ. Хвойные деревья: Тис ягодный Можжевельник в. | 2-3 2,5 1,5-2 0,5 0,6 0,7 0,5 1-2 1,5 1,5-2 0,2 0,5-0,7 1-1,5 0.5-0.75 0,5-0,75 0,3 0,2-0,5 0,2-0,5 | 5,5 5-8 5,5 3.3 2,5-3 1,5-2 2,1 2,5 3-4 2,5 1,5-2 2-3 1-1,5 1,4 0,5-1 0,5-1 | 7-8 10-12 9,5 8.4 6,5 5,3 4-5 8-9 7-8 7,5 5-6 3-4 2-3 2-3 | 14-16 18-20 13-16 12-15 12-15 15-18 8-10 5,5-6 8-12 8,5 6-8 5-6 | 18-20 27,7 20-24 18-20 20-22 15-16 7-7,5 15-20 10-12 7-8 | 33-34 25-30 23-24 25-28 9-10 |
Таблица 4. Классификация древесных пород по долговечности
| Группы долговечности | Продолжительность жизни, лет | |
| Деревья | Кустарники | |
| 1 – весьма долговечные 11- долговечные 111 – средней долговечнос. 1У – недолговечные | 500 и более | 100 и более |
| 200-500 | 50-100 | |
| 100-200 | 25-50 | |
| До 100 | До 25 |
Таблица 3. Предельная долговечность некоторых древесных
и кустарниковых пород
| Группа долговеч-ности | Древесные породы | Предельная долговеч-ность, лет | Кустарниковые породы | Предель- ная дол-говечнос лет |
| IV | Тис ягодный Дуб черешчатый Липа крупнолист. Сосна сибирская Лиственница Сосна обыкновен. Липа мелколистн. Вяз Тополь белый Ясень обыкновен. Груша Клен остролистн. Каштан конский Клен полевой Яблоня лесная Ива белая Осина Рябина обыкновенная | 800-1200 800-1000 800-1000 600 и бол. 500-600 300-400 300 и бол. 300 и бол. 300 и бол. 200-300 200-300 150-200 100-150 100-150 80-100 80-100 60-80 | Можжевельник Айва японская Калина обыкновен. Клен татарский Сирень обыкновен. Сосна горная Бузина черная Клен гиннала Лещина обыкновен. Ракитник «Золотой дождь» Смородина золот. Бузина красная Дейция Форзиция Чубушник Миндаль трехлоп. Спиреи Снежноягодник | 100 и б. 50 и бол 50 и бол 50 и бол 50 и бол 50-80 25-30 25-30 25-30 20-25 20-25 20-25 15-20 15-20 15-20 |
Долговечность резко снижается из-за загрязненности внешней среды пылью, вредными газами, недостаточности питательных веществ в почве, нарушения воздушного и водного режима почвы.
ОБЩИЕ СВЕДЕНИЯ О ДЕРЕВЬЯХ И КУСТАРНИКАХ, ИХ РОСТЕ И ДОЛГОВЕЧНОСТИ
Древесными растениями называются многолетние растения с деревянистыми надземными (стебли) и подземными (корни) частями.
Древесные растения по характеру развития стебля подразделяются на: а) деревья, б) кустарники и в) вьющиеся (лианы).
Деревья имеют хорошо выраженный один ствол, достигают больших размеров; обычно более долговечны, чем кустарники.
Кустарники достигают относительно небольших размеров, образуют уже от корня несколько почти равноценных ветвящихся стволов; обычно менее долговечны, чем деревья.
Кроме перечисленных, к древесным растениям можно отнести также близкие к ним полукустарники, занимающие промежуточное место между древесными и травянистыми растениями. К полукустарникам относятся растения, у которых стебли древеснеют не полностью, а лишь в нижней части, верхняя же часть стебля остается травянистой и ежегодноотмирает (например, у многих видов полыни). К полукустарникам относятся также такие растения, у которых стебли хотя и древеснеют полностью в однолетнем возрасте, но, закончив на второй год циклы цветения и плодоношения, отмирают (малина).
Обладая различными декоративными свойствами (размеры, форма, цвет), деревья, кустарники и полукустарники находят неодинаковое применение в зеленом строительстве.
Главным материалом объемных решений садово-парковых композиций являются деревья; кустарники и полукустарники служат преимущественно вспомогательным материалом. Лишь в малых объектах зеленого строительства (в небольших скверах и дворовых садиках), а также в специальных садах (например, в альпинариях) кустарники используются в качестве основного материала.
Различают древесные растения: а) вечнозеленые и б) листопадные.
Вечнозеленые имеют многолетние листья (или хвою), которые опадают не все сразу, а постепенно заменяются новыми листьями, так что растение всегда покрыто зелеными листьями.
Листопадные растения ежегодно сбрасывают все листья с наступлением неблагоприятных периодов вегетации (в умеренном и холодном климате — зимой; а в тропиках — в период засух).
Указанные биологические особенности древесных растений имеют важное значение при использовании их в парковом строительстве.
При использовании растений для декоративных целей необходимо учитывать, что растения являются живым материалом и декоративные качества их зависят как от свойств самого растения, так и от условий среды, в которых происходит их развитие. Кроме того, декоративные качества растений динамичны. Они в большей или меньшей мере изменяются в связи с развитием растения — возрастным и сезонным. Поэтому необходимо использовать декоративные качества растений в неразрывной связи как с биологическими особенностями растении, так и с условиями внешней среды.
Одним из важнейших для паркостроителя свойств древесных растений являются достигаемые ими размеры, быстрота роста и долговечность.
РАЗМЕРЫ
Размеры, достигаемые древесными растениями, являются важнейшим их качеством при решении задач как чисто утилитарных (защитные полосы), так и декоративных.
Размеры деревьев и кустарников зависят прежде всего от присущих каждому виду наследственных особенностей. Ими, например, определяется гораздо больший размер деревьев по сравнению с кустарниками.
В свою очередь как среди деревьев, так и среди кустарников одни виды достигают гораздо большей величины, чем другие.
Имеется много классификаций деревьев и кустарников по высоте роста и диаметру крон. Все они более или менее условны (табл. 1).
Классификация деревьев и кустарников по высоте
| Древесные растения | Классы высоты | Высота, м |
| Деревья | I (первой величины) II (втором величины) III (третьей величины) | 20 и более 10—20 5—10 |
| Кустарники | I (высокие) II (средней высоты) III (низкие) | 2—5 1—2 0,5—1 |
В качестве примеров приводим ниже распределение по классам высот наиболее’ известных видов деревьев и кустарников.
ДЕРЕВЬЯ ПЕРВОЙ ВЕЛИЧИНЫ (20ми выше):
хвойные — ель обыкновенная, лиственница сибирская, пихта кавказская, сосна обыкновенная;
лиственные — береза бородавчатая, бук, дуб черешчатый, ива белая, клен остролистный, липа крупнолистная, ольха черная,тополь белый, тополь черный,ясень обыкновенный.
ДЕРЕВЬЯ ВТОРОЙ ВЕЛИЧИНЫ( 10 – 20м ):
хвойные — ель канадская, лиственница японская, пихта бальзамическая, сосна пицундская, тис ягодный;
лиственные—береза пушистая, граб, груша обыкновенная, ива ломкая, клен полевой, липа мелколистная, шелковица белая.
ДЕРЕВЬЯ ТРЕТЬЕЙ ВЕЛИЧИНЫ (5-10м):
хвойные — можжевельник виргинский, можжевельник высокий, сосна Банкса;
лиственные — айва обыкновенная, клен татарский, рябина обыкновенная, черемуха обыкновенная, яблоня ягодная (я. сибирская).
КУСТАРНИКИ ВЫСОКИЕ (2—5м):
хвойные — кедровый стланец, можжевельник обыкновенный;
лиственные — акация желтая, бересклет европейский, боярышник обыкновенный, бузина черная, бузина красная, калина обыкновенная, клен гиннала, лещина, лох узколистный, сирень обыкновенная.
КУСТАРНИКИ СРЕДНЕЙ ВЫСОТЫ (1-2м ):
хвойные—сосна горная низкорослая;
лиственные — айва японская, барбарис обыкновенный, спирея острозубчатая, спирея иволистная, смородина золотистая.
КУСТАРНИКИ НИЗКИЕ (0,5-1м):
хвойные — можжевельник казацкий;
лиственяые— дафна обыкновенная (волчеягодник обыкновенный), дейция изящная, дрок красильный, миндаль низкий (м.
степной, бобовник), спирея зазубренная, спирея японская.
КРОНА
Развитие кроны в ширину у деревьев (и кустарников) обычно связано с их ростом в высоту.
Деревья первой величины имеют широкую крону (диаметром более 10м ), например дуб, клен остролистный, ясень; деревья второй величины — крону средних размеров (диаметром 5—10м )—граб, груша обыкновенная, клен полевой; деревья третьей
величины—узкую крону (диаметром 2 – 5 м) рябина обыкновенная, чер новенная, яблоня ягодная.
Однако из этого правила имеются исключения. Есть деревья первой величины с пирамидальной или колонновиднон кроной, например тополи пирамидальные, кипарис
пирамидальный, имеющие диаметр кроны — 3мпри высоте 20—30 м. В то же время некоторые невысокие виды деревьев имеют широкую раскидистую крону, как у деревьев первой величины. Так, например, альбиция (акация) ленкоранская, по высоте относящаяся к деревьям второй и даже третьей величины, имеет очень широкую зонтиковидную крону (у взрослых деревьев до 10—15м ).
Для кустарников могут быть приняты следующие диаметры кроны: у высоких кустарников — 3—5 ми более, у кустарников средней высоты—1—3 м, у низких кустарников — 0,5—1 м.
Однако среди высоких кустарников имеются виды и формы с более узкими кронами, чем
указано для этой группы; вместе с тем у низкорослых кустарников подушечной и стелющейся форм диаметр кроны иногда больше указанного для высоких кустарников.
БЫСТРОТА РОСТА
Быстрота роста является весьма важным свойством древесных растений.
Быстрорастущие растения раньше дают декоративный эффект и раньше проявляют защитные свойства.
Быстрорастущими считаются такие древесные растения, которые в молодом возрасте растут быстрее других.
Прирост древесных растений идет в трех направлениях: а) по высоте, б) по ширине (диаметру) кроны и в) по толщине (диаметру) ствола. Из них при оценке быстроты роста древесной породы для целей паркостроительства обычно принимается во внимание лишь прирост в высоту. Однако в известных случаях имеет существенное значение и прирост толщины ствола (например, при подборе деревьев для аллейных посадок), а также прирост по ширине кроны (у одиночных экземпляров — «солитеров» — и в аллейных посадках).
Быстрота роста деревьев в высоту характеризуется размером ежегодного прироста длины стебля. Величина этого прироста у разных видов древесных растений весьма различна. Быстрорастущие породы обладают в то же время большим ежегодным приростом боковых побегов, у медленно растущих годичный прирост побегов значительно меньше.
Но у всех видов древесных растений наблюдается общая закономерность: в первые годы развития дерева годичный прирост сравнительно невелик, затем он увеличивается, достигая к определенному возрасту наибольшем величины, потом постепенно уменьшается; наконец, в старости рост деревьев в высоту почти приостанавливается. Наиболее интенсивный прирост в высоту у большинства видов деревьев наблюдается в возрасте от 10 до 20—30 лет.
Размеры годичного прироста стебля н побегов в период интенсивного роста дерева и являются объективными показателями быстроты его роста (в оптимальных условиях среды).
Величина годичного прироста стебля и боковых побегов у одного и того же вида сильно колеблется в зависимости от условий среды: количества тепла, осадков и света, качества почвы. Так, например, количество тепла, обусловленное географической широтой места произрастания, оказывает следующее влияние на размеры годичного прироста побегов у сосны обыкновенной: в средней полосе СССР он достигает наибольшего размера в 25 лет, южнее, например в Воронежской области,—в 15 лет, а в северной полосе—в 40 лет и позже.
Для практических целей паркостроительства можно принять следующую классификацию древесных пород (деревьев н кустарников) по быстроте роста в высоту, т. е. по среднему ежегодному приросту в период наиболее интенсивного роста.
Дата добавления: 2016-03-10; просмотров: 1897;
ПОСМОТРЕТЬ ЕЩЕ:
Ассортимент растений для зеленого строительства определяется исходя из сложного комплекса требований, учитывающих климатические условия данного района, целевое назначение объекта, природные особенности озеленяемой площади (почвы, рельеф, гидрология, инсоляция и др.), архитектурно-планировочную ситуацию.
При выборе материала в ходе ландшафтного проектирования огромное значение имеют эстетические особенности деревьев и кустарников, они характеризуются:
- изменением размеров,
- формы,
- цвета,
- облиственности, что обусловлено их ростом и развитием,
- сезонными циклами жизнедеятельности.
Каждое растение, особенно отдельно стоящее, имеет свои индивидуальны черты. В то же время в групповых посадках деревья и кустарники обладают способностью «притираться» друг к другу, образуя не набор отдельных растений, а единую взаимосвязанную группу, обладающую определенной способностью к саморегулированию и формированию уравновешенного объема.
При формировании объемно-пространственной композиции парка габитусы насаждений, их высота, долговечность и динамика развития по отношению друг к другу имеют главенствующее значение. Каждый вид растений характеризуется присущей ему высотой, формой и силуэтом кроны. Условно можно разделить деревья на три типа по высоте:
- высокие (20…30 м и более) — ель и сосна обыкновенные, бук, липа и т. д.;
- средние (12…20 м),
- низкие (8…12 м) — к ним относятся полудеревья-полукустарники — черемуха, лох, рябина и др.
Особое значение в лесоводственно-мелиоративном отношении имеет характер развития крон деревьев, составляющих насаждения лесных полос.
Определения формы кроны были сделаны более чем у 30 тыс. деревьев; выделено несколько наиболее характерных типов крон:
- «волк» — очень широкая, раскидистая, агрессивная крона;
- широкая — с радиусом более 3 м;
- нормальная— с радиусом от 1,5 до 3,0 м,
- узкая — с радиусом менее 1,5 м;
- однобокая — развитая в одну сторону;
- флагообразная — узкая однобокая крона, обычно с наклоненной в ту же сторону вершиной;
- плоская — развитая лишь в одной вертикальной плоскости;
- приплюснутая — грибообразная крона, характерная для деревьев, испытывающих сильное угнетение сверху (например, дуб под березовым пологом).
Помимо общего рисунка кроны большое значение имеет характер ветвления, рисунок и архитектоника основных «скелетных» ветвей, особенно в те времена года, когда дерево сбрасывает листву.
Художественная выразительность того или иного вида растений определяется размерами, формой, оттенком, фактурой и подвижностью листвы, а также ее цветовой динамикой в различные времена года, характером, фактурой и цветом коры, характером цветения и плодоношения. Деревья, обладающие большой высотой, кряжистым толстым стволом и мощными ветвями, воспринимаются олицетворяющими силу, прочность. Тонкие стволики и ветви, свисающие ажурные кроны ассоциируются с грустью, нежностью, хрупкостью. Сообразно этому определяется их местоположение в ландшафте парка. Например, высокие мощные деревья, расположенные одиночно и группами на больших открытых полянах, позволяют осматривать их с разных расстояний. Плакучие формы, как правило, размещаются на небольших территориях, у водоемов, в виде одиночных и групповых посадок.
Характер ветвленияи облиствления определяет ажурность или плотность кроны дерева или кустарника и обусловливает их художественные особенности. Крона в зависимости от своей формы, отношения к высоте штамба, плотности, цветовой окраски в большей или меньшей степени влияет на «массу» всего растения. У одиночных экземпляров, растущих на открытом месте, развивается более мощная раскидистая крона, а ствол низкий и толстый.
Примером этому могут служить дуб черешчатый, вяз.
Архитектонические качества зеленых насаждений наиболее выражены:
- размерами,
- характером ветвления,
- формой кроны и соотношением ее со стволом.
Эти факторы в значительной мере определяют возможности композиционного пространственного использования растений и условия их восприятия в парковом ансамбле. Так, по наблюдениям В. А. Артамонова, если при дальних дистанциях осмотра основную роль играют высота и силуэт рассматриваемых насаждений, то при ближнем восприятии (в пределах одной высоты) приобретают главное значение декоративные детали, например листва и ее фактура, текстура коры, рисунок сучьев.
Подбор ассортимента растений для создания композиций является сложной задачей, поэтому возникает острая необходимость в анализе их декоративных качеств и классификации по следующим признакам:
- Высота древесных растений (I, II, III величины) и форма крон (регулярная, иррегулярная).
- Тип ветвления и цвет ветвей.
- Форма стволов, структура и цвет коры.
- Характер облиствения (грубая, средняя, тонкая фактура) и цвет листьев.
- Морфология и окраска цветков и плодов.
Сложность построения паркового пейзажа заключается не только в подборе растений, но и учете изменений их внешнего облика и цвета в течение года, а также возраста.
Социальные кнопки для Joomla
Высокие стволы и густые кроны затеняют соседский участок, мощная корневая система забирается на чужую плодородную территорию, поэтому деревья от соседского забора нужно сажать на определенном расстоянии. В действующем российском законодательстве существуют технические нормы и требования к загородным застройкам. Пункт 6.7 СНиП 30-02-97 гласит: минимальное расстояние до соседского участка должно составлять для стволов высоких деревьев – 4 м, среднерослых – 2 м, кустарников – 1 м.
Разъяснений, какие породы деревьев относятся к каким категориям высоты, в СНиП нет, но воспользуемся справочной литературой по садоводству или лесному хозяйству. Высота зависит от породы. Итак, растения бывают высокорослые (более 15 м в высоту), среднерослые (10-15 м) и низкорослые (до 10 м). К высокорослым относятся дуб, береза, клен, тополь, ива, ель, сосна и плодовые яблоня, груша, черешня. Соответственно, от соседского забора их нужно сажать на расстоянии не менее 3-4 м. Среднерослые: вишня, алыча, калина, слива, облепиха, орешник – не менее 2 м. Низкорослыми считаются карликовые плодовые деревья, декоративные и ягодные кустарники: смородина, виноград, малина.
Их нужно сажать на расстоянии не менее 1 метра от забора. Важно не только не помешать соседям, но и сохранить собственный забор и фундамент ограждения от разрушения корневой системой растений, поэтому расстояние посадки в 2,5-3 м от собственного забора будет оптимальным.
Запись опубликована в рубрике Основная. Добавьте в закладки постоянную ссылку.
Источник
Диаметр кроны дерева
Предмет
Воспроизводство и переработка лесных ресурсов
Разместил
🤓 AlainHast
👍 Проверено Автор24
поперечник кроны дерева, измеряемый по ее проекции на земную поверхность.
Научные статьи на тему «Диаметр кроны дерева»
Защита растений в процессе строительства
погибшие деревья, а пни сжигают….
;
деревья огораживают щитами из досок, высота которых составляет 2-2,4 метра;
особо ценные породы деревьев…
Схемы защиты деревьев по время строительства….
методику:
объем одного дерева определяется исходя из диаметра ствола на высоте 1,3 метра;
объем кустарников…
условия, но минимальная защита позволит избежать механических повреждений ствола, кроны и корневой системы

Статья от экспертов
Выявление взаимосвязи диаметра крон деревьев с различными таксационными показателями в северо-таежном лесном районе
Для повышения точности оценки лесных насаждений по аэрофотоснимкам методом автоматизированного дешифрирования необходимо глубокое изучение степени и формы взаимосвязи между таксационными и дешифровочными показателями. Исследование направлено на реализацию идеи о выявлении наиболее достоверных (оптимальных) зависимостей между данными показателями и последующей разработкой уравнений при их расчете. Выявлены взаимосвязи таксационного диаметра с таксационно-дешифровочными показателями древостоя такими как высота и диаметр крон. В результате анализа зависимостей между полнотой древостоя и сомкнутостью крон деревьев выявлена слабая связь.
Природные особенности широколиственных лесов
Одно из самых крупных и долгорастущих деревьев. Как правило, их больше всего среди других деревьев….
Высокое растение (30-40 м в высоту) с прямым стволом, светло-серой корой и ажурной, рыхлой кроной….
в диаметре….
Существуют леса, в которых отсутствует травянисты покров и подлесок из-за наличия плотных и высоких крон…
деревьев.

Статья от экспертов
Взаємозв’язок між параметрами крон та іншими таксаційними показниками дерев гіркокаштана звичайного в зелених насадженнях міста Києва
Міські зелені насадження зазнають впливу урбанізованого середовища, що негативно позначається на життєдіяльності рослин. Умови росту зелених насаджень на урбанізованих територіях істотно відрізняються від природних. Наведено особливості методичного підходу проведення замірів основних біометричних параметрів дерев в умовах урбанізованого середовища. Здійснено статистичний аналіз дослідних даних. Викладено результати дослідження зв’язку параметрів крони з іншими таксаційними показниками дерев. На основі кореляційного аналізу встановлено, що об’єм крони потрібно моделювати залежно від діаметра крони та діаметра дерева на висоті грудей.
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек
Важнейшими характеристиками, которые учитываются при использовании деревьев и кустарников в озеленении, являются их размеры. В табл.1 приводится условная классификация наиболее распространенных деревьев и кустарников по высоте во взрослом состоянии. Все деревья и кустарники относятся к трем классам по высоте:
Деревья: Кустарники:
1 класс – от 20 м и выше 1 класс – от 3 м и выше
11 класс – от 10 м до 20 м 11 класс – от 1 м до 3 м
111 класс – до 10 м 111 класс – до 1 м
Обычно деревья первой величины имеют широкую (более 10 м в диаметре) крону – дуб, клен остролистный, ясень.
Крону средних размеров (диаметром 5-10 м) имеют деревья второй величины – груша обыкновенная, клен полевой.
Таблица 1. Классификация деревьев и кустарников по высоте
| Класс высоты | Высота, м | Хвойные | Лиственные |
| Деревья первой величины | 20 и более | Ель обыкновен. ель колючая, лиственница европейская, л. сибирская, пихта сибирская, сосна Веймутова, сосна кедровая сибирская, с.обыкновенная | Береза бородавчатая, б.пушистая, вяз гладкий, обыкновенный, вяз шершавый, дуб черешчатый, дуб красный, ива белая, каштан конский, клен остролистный, липа крупнолистная, л. мелколистная, орех маньчжурский, осина (тополь дрожащий), тополь белый, т.берлинский, т.душистый, т. черный, ясень обыкновенный |
| Деревья второй величины | 10-20 | Можжевельник виргинский, мож. казацкий, тис ягодный, туя западная. Можжевельник высокий, сосна румелийская, с.горная, | Груша обыкновенная, акация белая, ива ломкая, клен полевой, клен ясенелистный, шелковица белая |
| Деревья третьей величины | до 10 | кедровый стланец, можжевельник обыкновенный | Рябина обыкновенная, черемуха обыкновенная, черемуха виргинская, вишня обыкновенная, груша уссурийская, клен татарский, к. гиннала, яблоня сибирская (ягодная) |
| Кустарники высокие | 3 м и более | Сосна горная низкорослая, кипарисовик горохоплодный, можжевельник средний, м. виргинский, туи низкорослые | Акация желтая, бересклет европейский, боярышник обыкновенный, б. сибирский, бузина красная, гортензия метельчатая, жимолость татарская, ирга обыкновенная, калина обыкновенная, лещина обыкновенная, ракитник «Золотой дождь», роза краснолистная, сирень венгерская, с. обыкновенная, снежноягодник кистевой, спирея калинолистная, спирея средняя, чубушник венечный |
| Кустарники средней высоты | 1-3 | Кипарисовик Лосона, можжевельник горизонтальный, м. казацкий, м.обыкновенный, туя западная | Айва японская, барбарис обыкновенный, дерен белый сибирский, жимолость синяя, жимолость съедобная, кизильник блестящий, лох серебристый, малина душистая, роза коричная, р. морщинистая, смородина золотистая, смородина черная, красная, спирея иволистная, с. острозубчатая, с. рябинолистная, с. Ван-Гутта |
| Кустарники низкие | до 1 | Барбарис Тунберга, дафна (волчеягодник) обыкновенная, дейция изящная, дрок красильный, кизильник горизонтальный, миндаль низкий, роза миниатюрная, спирея Бумальда, с. японская |
Узкую крону (диаметром 2-5 м) имеют деревья третьей величины – рябина обыкновенная, черемуха обыкновенная, яблоня ягодная.
У кустарников обычно диаметр кроны имеет следующие размеры: у высоких – 3-5 м, у кустарников средней высоты – 1-3 м, у низких – 0,5-1 м.
Быстрота роста
Важным свойством древесных растений является быстрота роста. Прирост древесных растений определяется по трем критериям: высота, ширина (диаметр кроны), толщина (диаметр ствола).
Быстрота роста деревьев в высоту определяется размером ежегодного прироста высоты стебля. Для практических целей паркостроительства обычно принимают во внимание прирост древесных пород в высоту (табл.2)
Таблица 2. Классификация деревьев и кустарников по быстроте роста в высоту
| Ежегодный при-рост | Класс быстроты роста в высоту | Хвойные | Лиственные | ||
| До 2 м и более До 1 м До 0,5-0,6м До 0,25-0,3 До 0,15 м и менее | Весьма быстро- расту- щие: деревья: кустар- ники: Быстро-расту-щие: деревья: кустар-ники: Умерен-ного роста: деревья: кустар-ники: Медлен-норас-тущие: деревья: кустар- ники: Весьма медлен-норас-тущие: деревья: кустар-ники: | Лиственница евро-пейская, л. сибир-ская, сосна обыкновенная, с. Веймутова, ель обыкновенная Пихта сибирская, ель колючая, можжевельник виргинский, туя западная Сосна горная низ-корослая Сосна сибирская кедровая Можжевельник казацкий, м. обык-новенный Кедровый стланец, тис ягодный, карликовые формы хвойных пород Все карликовые кустарниковые формы хвойных древесных пород | Тополь бальзамический, т. канадский, т. черный, осина, ива белая, береза бородавчатая, клен ясенелистный Акация желтая, бузина черная, б. красная, чубушники, дейция городчатая, форзиция, спирея калинолистная, с. рябинолистная, с. Ван-Гутта Вяз шершавый, в. мелколистный, дуб красный,ясень обыкновенный Бересклет европейский, дерен сибирский, жимолость татарская, калина обыкновенная, лещина обыкновенная, ракитник «золотой дождь», смородина золотистая Дуб черешчатый, клен остролистный, к. полевой, липа крупнолистная, л. мелколистная, Айва японская, клен гиннала, сирень обыкновенная Груша лесная, яблоня сибирская Боярышник обыкновенный, ирга обыкновенная, облепиха Карликовые формы лиственных пород Волчеягодник обыкновенный, все карликовые формы лиственных пород | ||
Прирост кроны в ширину у древесных пород, как правило, отстает от прироста в высоту, но продолжается даже после прекращения прироста в высоту.
Таблица 3. Высота основных видов древесных растений, м
| Породы | Возраст древесных растений, лет | ||||||
| Весьма быстрорастущ.: Тополь канадский Т. берлинский Т. черный Береза бородавчат. | 2,5 | 13,5 | 28,5 | ||||
| Быстрорастущие Лиственные: Ясень обыкновен. Вяз мелколистн. Дуб красный Хвойные деревья: Лиственница евр. Л.сибирская Сосна Веймутова С. обыкновенная Ель обыкновенная Умеренного роста Лиственные: Клен остролистн. Дуб черешчатый Вяз гладкий Липа крупнолистн. Л. мелколистная Хвойные деревья: Пихта сибирская Ель колючая Медленнорастущ. Лиственные: Груша обыкновен. Яблоня ягодная Хвойные деревья: Сосна сибирская Туя западная Весьма медленнорастущ. Хвойные деревья: Тис ягодный Можжевельник в. | 2-3 2,5 1,5-2 0,5 0,6 0,7 0,5 1-2 1,5 1,5-2 0,2 0,5-0,7 1-1,5 0.5-0.75 0,5-0,75 0,3 0,2-0,5 0,2-0,5 | 5,5 5-8 5,5 3.3 2,5-3 1,5-2 2,1 2,5 3-4 2,5 1,5-2 2-3 1-1,5 1,4 0,5-1 0,5-1 | 7-8 10-12 9,5 8.4 6,5 5,3 4-5 8-9 7-8 7,5 5-6 3-4 2-3 2-3 | 14-16 18-20 13-16 12-15 12-15 15-18 8-10 5,5-6 8-12 8,5 6-8 5-6 | 18-20 27,7 20-24 18-20 20-22 15-16 7-7,5 15-20 10-12 7-8 | 33-34 25-30 23-24 25-28 9-10 |
Таблица 4. Классификация древесных пород по долговечности
| Группы долговечности | Продолжительность жизни, лет | |
| Деревья | Кустарники | |
| 1 – весьма долговечные 11- долговечные 111 – средней долговечнос. 1У – недолговечные | 500 и более | 100 и более |
| 200-500 | 50-100 | |
| 100-200 | 25-50 | |
| До 100 | До 25 |
Таблица 3. Предельная долговечность некоторых древесных
и кустарниковых пород
| Группа долговеч-ности | Древесные породы | Предельная долговеч-ность, лет | Кустарниковые породы | Предель- ная дол-говечнос лет |
| IV | Тис ягодный Дуб черешчатый Липа крупнолист. Сосна сибирская Лиственница Сосна обыкновен. Липа мелколистн. Вяз Тополь белый Ясень обыкновен. Груша Клен остролистн. Каштан конский Клен полевой Яблоня лесная Ива белая Осина Рябина обыкновенная | 800-1200 800-1000 800-1000 600 и бол. 500-600 300-400 300 и бол. 300 и бол. 300 и бол. 200-300 200-300 150-200 100-150 100-150 80-100 80-100 60-80 | Можжевельник Айва японская Калина обыкновен. Клен татарский Сирень обыкновен. Сосна горная Бузина черная Клен гиннала Лещина обыкновен. Ракитник «Золотой дождь» Смородина золот. Бузина красная Дейция Форзиция Чубушник Миндаль трехлоп. Спиреи Снежноягодник | 100 и б. 50 и бол 50 и бол 50 и бол 50 и бол 50-80 25-30 25-30 25-30 20-25 20-25 20-25 15-20 15-20 15-20 |
Долговечность резко снижается из-за загрязненности внешней среды пылью, вредными газами, недостаточности питательных веществ в почве, нарушения воздушного и водного режима почвы.
1234567Следующая ⇒
ОБЩИЕ СВЕДЕНИЯ О ДЕРЕВЬЯХ И КУСТАРНИКАХ, ИХ РОСТЕ И ДОЛГОВЕЧНОСТИ
Древесными растениями называются многолетние растения с деревянистыми надземными (стебли) и подземными (корни) частями.
Древесные растения по характеру развития стебля подразделяются на: а) деревья, б) кустарники и в) вьющиеся (лианы).
Деревья имеют хорошо выраженный один ствол, достигают больших размеров; обычно более долговечны, чем кустарники.
Кустарники достигают относительно небольших размеров, образуют уже от корня несколько почти равноценных ветвящихся стволов; обычно менее долговечны, чем деревья.
Кроме перечисленных, к древесным растениям можно отнести также близкие к ним полукустарники, занимающие промежуточное место между древесными и травянистыми растениями. К полукустарникам относятся растения, у которых стебли древеснеют не полностью, а лишь в нижней части, верхняя же часть стебля остается травянистой и ежегодноотмирает (например, у многих видов полыни). К полукустарникам относятся также такие растения, у которых стебли хотя и древеснеют полностью в однолетнем возрасте, но, закончив на второй год циклы цветения и плодоношения, отмирают (малина).
Обладая различными декоративными свойствами (размеры, форма, цвет), деревья, кустарники и полукустарники находят неодинаковое применение в зеленом строительстве.
Главным материалом объемных решений садово-парковых композиций являются деревья; кустарники и полукустарники служат преимущественно вспомогательным материалом. Лишь в малых объектах зеленого строительства (в небольших скверах и дворовых садиках), а также в специальных садах (например, в альпинариях) кустарники используются в качестве основного материала.
Различают древесные растения: а) вечнозеленые и б) листопадные.
Вечнозеленые имеют многолетние листья (или хвою), которые опадают не все сразу, а постепенно заменяются новыми листьями, так что растение всегда покрыто зелеными листьями.
Листопадные растения ежегодно сбрасывают все листья с наступлением неблагоприятных периодов вегетации (в умеренном и холодном климате — зимой; а в тропиках — в период засух).
Указанные биологические особенности древесных растений имеют важное значение при использовании их в парковом строительстве.
При использовании растений для декоративных целей необходимо учитывать, что растения являются живым материалом и декоративные качества их зависят как от свойств самого растения, так и от условий среды, в которых происходит их развитие. Кроме того, декоративные качества растений динамичны. Они в большей или меньшей мере изменяются в связи с развитием растения — возрастным и сезонным. Поэтому необходимо использовать декоративные качества растений в неразрывной связи как с биологическими особенностями растении, так и с условиями внешней среды.
Одним из важнейших для паркостроителя свойств древесных растений являются достигаемые ими размеры, быстрота роста и долговечность.
РАЗМЕРЫ
Размеры, достигаемые древесными растениями, являются важнейшим их качеством при решении задач как чисто утилитарных (защитные полосы), так и декоративных.
Размеры деревьев и кустарников зависят прежде всего от присущих каждому виду наследственных особенностей. Ими, например, определяется гораздо больший размер деревьев по сравнению с кустарниками.
В свою очередь как среди деревьев, так и среди кустарников одни виды достигают гораздо большей величины, чем другие.
Имеется много классификаций деревьев и кустарников по высоте роста и диаметру крон. Все они более или менее условны (табл. 1).
Таблица 1.
Классификация деревьев и кустарников по высоте
| Древесные растения | Классы высоты | Высота, м |
| Деревья | I (первой величины) II (втором величины) III (третьей величины) | 20 и более 10—20 5—10 |
| Кустарники | I (высокие) II (средней высоты) III (низкие) | 2—5 1—2 0,5—1 |
В качестве примеров приводим ниже распределение по классам высот наиболее’ известных видов деревьев и кустарников.
а) ДЕРЕВЬЯ
ДЕРЕВЬЯ ПЕРВОЙ ВЕЛИЧИНЫ (20ми выше):
хвойные — ель обыкновенная, лиственница сибирская, пихта кавказская, сосна обыкновенная;
лиственные — береза бородавчатая, бук, дуб черешчатый, ива белая, клен остролистный, липа крупнолистная, ольха черная,тополь белый, тополь черный,ясень обыкновенный.
ДЕРЕВЬЯ ВТОРОЙ ВЕЛИЧИНЫ( 10 – 20м ):
хвойные — ель канадская, лиственница японская, пихта бальзамическая, сосна пицундская, тис ягодный;
лиственные—береза пушистая, граб, груша обыкновенная, ива ломкая, клен полевой, липа мелколистная, шелковица белая.
ДЕРЕВЬЯ ТРЕТЬЕЙ ВЕЛИЧИНЫ (5-10м):
хвойные — можжевельник виргинский, можжевельник высокий, сосна Банкса;
лиственные — айва обыкновенная, клен татарский, рябина обыкновенная, черемуха обыкновенная, яблоня ягодная (я. сибирская).
б) КУСТАРНИКИ
КУСТАРНИКИ ВЫСОКИЕ (2—5м):
хвойные — кедровый стланец, можжевельник обыкновенный;
лиственные — акация желтая, бересклет европейский, боярышник обыкновенный, бузина черная, бузина красная, калина обыкновенная, клен гиннала, лещина, лох узколистный, сирень обыкновенная.
КУСТАРНИКИ СРЕДНЕЙ ВЫСОТЫ (1-2м ):
хвойные—сосна горная низкорослая;
лиственные — айва японская, барбарис обыкновенный, спирея острозубчатая, спирея иволистная, смородина золотистая.
КУСТАРНИКИ НИЗКИЕ (0,5-1м):
хвойные — можжевельник казацкий;
лиственяые— дафна обыкновенная (волчеягодник обыкновенный), дейция изящная, дрок красильный, миндаль низкий (м.
степной, бобовник), спирея зазубренная, спирея японская.
КРОНА
Развитие кроны в ширину у деревьев (и кустарников) обычно связано с их ростом в высоту.
Деревья первой величины имеют широкую крону (диаметром более 10м ), например дуб, клен остролистный, ясень; деревья второй величины — крону средних размеров (диаметром 5—10м )—граб, груша обыкновенная, клен полевой; деревья третьей
величины—узкую крону (диаметром 2 – 5 м) рябина обыкновенная, чер новенная, яблоня ягодная.
Однако из этого правила имеются исключения. Есть деревья первой величины с пирамидальной или колонновиднон кроной, например тополи пирамидальные, кипарис
пирамидальный, имеющие диаметр кроны — 3мпри высоте 20—30 м. В то же время некоторые невысокие виды деревьев имеют широкую раскидистую крону, как у деревьев первой величины. Так, например, альбиция (акация) ленкоранская, по высоте относящаяся к деревьям второй и даже третьей величины, имеет очень широкую зонтиковидную крону (у взрослых деревьев до 10—15м ).
Для кустарников могут быть приняты следующие диаметры кроны: у высоких кустарников — 3—5 ми более, у кустарников средней высоты—1—3 м, у низких кустарников — 0,5—1 м.
Однако среди высоких кустарников имеются виды и формы с более узкими кронами, чем
указано для этой группы; вместе с тем у низкорослых кустарников подушечной и стелющейся форм диаметр кроны иногда больше указанного для высоких кустарников.
БЫСТРОТА РОСТА
Быстрота роста является весьма важным свойством древесных растений.
Быстрорастущие растения раньше дают декоративный эффект и раньше проявляют защитные свойства.
Быстрорастущими считаются такие древесные растения, которые в молодом возрасте растут быстрее других.
Прирост древесных растений идет в трех направлениях: а) по высоте, б) по ширине (диаметру) кроны и в) по толщине (диаметру) ствола. Из них при оценке быстроты роста древесной породы для целей паркостроительства обычно принимается во внимание лишь прирост в высоту. Однако в известных случаях имеет существенное значение и прирост толщины ствола (например, при подборе деревьев для аллейных посадок), а также прирост по ширине кроны (у одиночных экземпляров — «солитеров» — и в аллейных посадках).
Быстрота роста деревьев в высоту характеризуется размером ежегодного прироста длины стебля. Величина этого прироста у разных видов древесных растений весьма различна. Быстрорастущие породы обладают в то же время большим ежегодным приростом боковых побегов, у медленно растущих годичный прирост побегов значительно меньше.
Но у всех видов древесных растений наблюдается общая закономерность: в первые годы развития дерева годичный прирост сравнительно невелик, затем он увеличивается, достигая к определенному возрасту наибольшем величины, потом постепенно уменьшается; наконец, в старости рост деревьев в высоту почти приостанавливается. Наиболее интенсивный прирост в высоту у большинства видов деревьев наблюдается в возрасте от 10 до 20—30 лет.
Размеры годичного прироста стебля н побегов в период интенсивного роста дерева и являются объективными показателями быстроты его роста (в оптимальных условиях среды).
Величина годичного прироста стебля и боковых побегов у одного и того же вида сильно колеблется в зависимости от условий среды: количества тепла, осадков и света, качества почвы. Так, например, количество тепла, обусловленное географической широтой места произрастания, оказывает следующее влияние на размеры годичного прироста побегов у сосны обыкновенной: в средней полосе СССР он достигает наибольшего размера в 25 лет, южнее, например в Воронежской области,—в 15 лет, а в северной полосе—в 40 лет и позже.
Для практических целей паркостроительства можно принять следующую классификацию древесных пород (деревьев н кустарников) по быстроте роста в высоту, т. е. по среднему ежегодному приросту в период наиболее интенсивного роста.
Дата добавления: 2016-03-10; просмотров: 1897;
ПОСМОТРЕТЬ ЕЩЕ:
Ассортимент растений для зеленого строительства определяется исходя из сложного комплекса требований, учитывающих климатические условия данного района, целевое назначение объекта, природные особенности озеленяемой площади (почвы, рельеф, гидрология, инсоляция и др.), архитектурно-планировочную ситуацию.
При выборе материала в ходе ландшафтного проектирования огромное значение имеют эстетические особенности деревьев и кустарников, они характеризуются:
- изменением размеров,
- формы,
- цвета,
- облиственности, что обусловлено их ростом и развитием,
- сезонными циклами жизнедеятельности.
Каждое растение, особенно отдельно стоящее, имеет свои индивидуальны черты. В то же время в групповых посадках деревья и кустарники обладают способностью «притираться» друг к другу, образуя не набор отдельных растений, а единую взаимосвязанную группу, обладающую определенной способностью к саморегулированию и формированию уравновешенного объема.
При формировании объемно-пространственной композиции парка габитусы насаждений, их высота, долговечность и динамика развития по отношению друг к другу имеют главенствующее значение. Каждый вид растений характеризуется присущей ему высотой, формой и силуэтом кроны. Условно можно разделить деревья на три типа по высоте:
- высокие (20…30 м и более) — ель и сосна обыкновенные, бук, липа и т. д.;
- средние (12…20 м),
- низкие (8…12 м) — к ним относятся полудеревья-полукустарники — черемуха, лох, рябина и др.
Особое значение в лесоводственно-мелиоративном отношении имеет характер развития крон деревьев, составляющих насаждения лесных полос.
Определения формы кроны были сделаны более чем у 30 тыс. деревьев; выделено несколько наиболее характерных типов крон:
- «волк» — очень широкая, раскидистая, агрессивная крона;
- широкая — с радиусом более 3 м;
- нормальная— с радиусом от 1,5 до 3,0 м,
- узкая — с радиусом менее 1,5 м;
- однобокая — развитая в одну сторону;
- флагообразная — узкая однобокая крона, обычно с наклоненной в ту же сторону вершиной;
- плоская — развитая лишь в одной вертикальной плоскости;
- приплюснутая — грибообразная крона, характерная для деревьев, испытывающих сильное угнетение сверху (например, дуб под березовым пологом).
Помимо общего рисунка кроны большое значение имеет характер ветвления, рисунок и архитектоника основных «скелетных» ветвей, особенно в те времена года, когда дерево сбрасывает листву.
Художественная выразительность того или иного вида растений определяется размерами, формой, оттенком, фактурой и подвижностью листвы, а также ее цветовой динамикой в различные времена года, характером, фактурой и цветом коры, характером цветения и плодоношения. Деревья, обладающие большой высотой, кряжистым толстым стволом и мощными ветвями, воспринимаются олицетворяющими силу, прочность. Тонкие стволики и ветви, свисающие ажурные кроны ассоциируются с грустью, нежностью, хрупкостью. Сообразно этому определяется их местоположение в ландшафте парка. Например, высокие мощные деревья, расположенные одиночно и группами на больших открытых полянах, позволяют осматривать их с разных расстояний. Плакучие формы, как правило, размещаются на небольших территориях, у водоемов, в виде одиночных и групповых посадок.
Характер ветвленияи облиствления определяет ажурность или плотность кроны дерева или кустарника и обусловливает их художественные особенности. Крона в зависимости от своей формы, отношения к высоте штамба, плотности, цветовой окраски в большей или меньшей степени влияет на «массу» всего растения. У одиночных экземпляров, растущих на открытом месте, развивается более мощная раскидистая крона, а ствол низкий и толстый.
Примером этому могут служить дуб черешчатый, вяз.
Архитектонические качества зеленых насаждений наиболее выражены:
- размерами,
- характером ветвления,
- формой кроны и соотношением ее со стволом.
Эти факторы в значительной мере определяют возможности композиционного пространственного использования растений и условия их восприятия в парковом ансамбле. Так, по наблюдениям В. А. Артамонова, если при дальних дистанциях осмотра основную роль играют высота и силуэт рассматриваемых насаждений, то при ближнем восприятии (в пределах одной высоты) приобретают главное значение декоративные детали, например листва и ее фактура, текстура коры, рисунок сучьев.
Подбор ассортимента растений для создания композиций является сложной задачей, поэтому возникает острая необходимость в анализе их декоративных качеств и классификации по следующим признакам:
- Высота древесных растений (I, II, III величины) и форма крон (регулярная, иррегулярная).
- Тип ветвления и цвет ветвей.
- Форма стволов, структура и цвет коры.
- Характер облиствения (грубая, средняя, тонкая фактура) и цвет листьев.
- Морфология и окраска цветков и плодов.
Сложность построения паркового пейзажа заключается не только в подборе растений, но и учете изменений их внешнего облика и цвета в течение года, а также возраста.
Социальные кнопки для Joomla
Высокие стволы и густые кроны затеняют соседский участок, мощная корневая система забирается на чужую плодородную территорию, поэтому деревья от соседского забора нужно сажать на определенном расстоянии. В действующем российском законодательстве существуют технические нормы и требования к загородным застройкам. Пункт 6.7 СНиП 30-02-97 гласит: минимальное расстояние до соседского участка должно составлять для стволов высоких деревьев – 4 м, среднерослых – 2 м, кустарников – 1 м.
Разъяснений, какие породы деревьев относятся к каким категориям высоты, в СНиП нет, но воспользуемся справочной литературой по садоводству или лесному хозяйству. Высота зависит от породы. Итак, растения бывают высокорослые (более 15 м в высоту), среднерослые (10-15 м) и низкорослые (до 10 м). К высокорослым относятся дуб, береза, клен, тополь, ива, ель, сосна и плодовые яблоня, груша, черешня. Соответственно, от соседского забора их нужно сажать на расстоянии не менее 3-4 м. Среднерослые: вишня, алыча, калина, слива, облепиха, орешник – не менее 2 м. Низкорослыми считаются карликовые плодовые деревья, декоративные и ягодные кустарники: смородина, виноград, малина.
Их нужно сажать на расстоянии не менее 1 метра от забора. Важно не только не помешать соседям, но и сохранить собственный забор и фундамент ограждения от разрушения корневой системой растений, поэтому расстояние посадки в 2,5-3 м от собственного забора будет оптимальным.
Запись опубликована в рубрике Основная. Добавьте в закладки постоянную ссылку.





![{ displaystyle { begin {align} { text {объем короны}} = { text {объем эквивалентного цилиндра}} = pi hr ^ {2} \ [5pt] = {} pi cdot { frac {({ text { толщина короны}}) times { sqrt {{ text {соотношение формы короны}} times { text {средний минимальный разброс короны}}}}} {4}} \ [5pt] { text { где средний минимальный размах короны}} = 2 times { text {средний максимальный радиус}} end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7e3604a529694a61cc03ac562f543ad4bf666ab)









