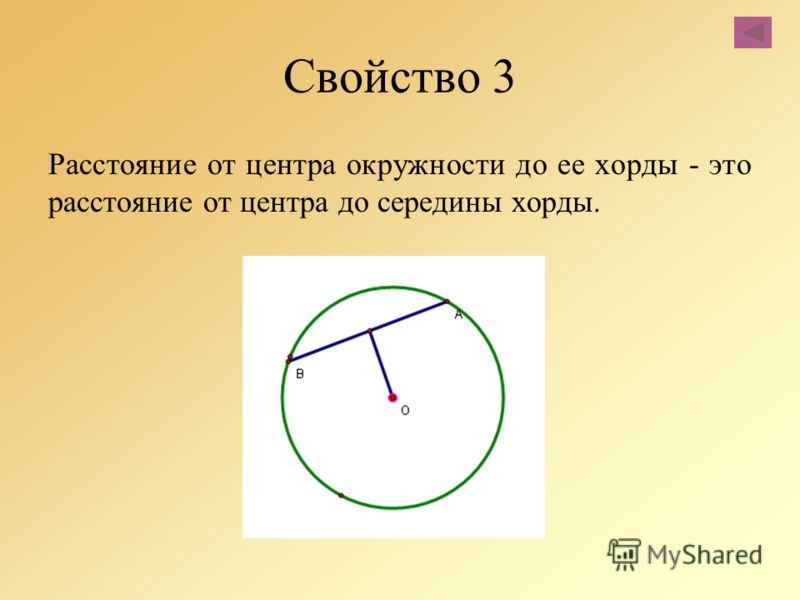
Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.
Сегмент круга
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Вычисление диаметра трубы по хорде
Бывают ситуации, когда необходимо измерить диаметр чего-либо, например, трубопровода, но нет возможности измерить длину окружности (из-за изоляции или температуры).
В этом случае можно применить метод вычисления диаметра по хорде. Для этого метода необходим только штангенциркуль.
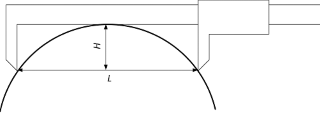
- Прикладываем его, как показано на рис. 1;
- измеряем длину L;
- измеряем высоту губок штангенциркуля Н;
- вычисляем диаметр по формуле D = (L 2 ⁄ 4H) + H или
- вычисляем радиус по формуле r = (L 2 + 4H 2 ) ⁄ 8H
Рисунок 1
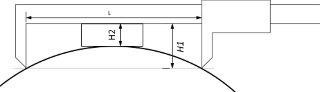
Если под рукой только «штангель» с длинными губками или не хватает его измеряемого диапазона можно применить какую-нибудь «проставку». В идеале подойдёт плоскопараллельная концевая мера… 😉 Её надо вставить, как показано на рисунке 2, и при вычислении, от длины губок отнять высоту этой «проставки». Н = Н1 – Н2
Рисунок 2
Точность этого метода зависит, только от инструмента, который Вы будете применять.
Геометрия круга
Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии.
Давайте сначала рассмотрим, какие у круга бывают части и как они называются.
- Окружность — линия, ограничивающая круг.
- Дуга — часть окружности.
- Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
- Хорда — отрезок, соединяющий две точки окружности.
- Сегмент — часть круга, ограниченная хордой и дугой.
- Сектор — часть круга, ограниченная двумя радиусами и дугой.
Интересующие нас величины и их обозначения:
Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.
- Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
- Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
- Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).
И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.
И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
1. Даны диаметр D и длина дуги L
; длина хорды 
;
высота сегмента 
; центральный угол 
.
2. Даны диаметр D и длина хорды X
; длина дуги 
;
высота сегмента ; центральный угол 
.
Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол 
.
3. Даны диаметр D и центральный угол φ
; длина дуги ;
длина хорды ; высота сегмента .
4. Даны диаметр D и высота сегмента H
; длина дуги ;
длина хорды ; центральный угол .
6. Даны длина дуги L и центральный угол φ
; диаметр 
;
длина хорды ; высота сегмента .
8. Даны длина хорды X и центральный угол φ
; длина дуги 
;
диаметр ; высота сегмента .
9. Даны длина хорды X и высота сегмента H
; длина дуги ;
диаметр ; центральный угол .
10. Даны центральный угол φ и высота сегмента H
; диаметр 
;
длина дуги ; длина хорды .
Внимательный читатель не мог не заметить, что я пропустил два варианта:
5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H
Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?
Задача эта сводится к решению уравнений: 
; — в варианте 5 
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.
Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:
длина окружности 
;
площадь круга 
;
площадь сектора 
;
площадь сегмента 
;
И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.
[spoiler title=”источники:”]
http://www.axwap.com/kipia/items/vychislenie-diametra-truby/vychislenie-diametra-truby.htm
[/spoiler]
HOUSEHAND.ru —
Сегмент — плоская фигура, заключённая между дугой и её хордой. Как частный случай, круговой сегмент: часть круга, ограниченная дугой окружности и её хордой или секущей.
Для начала расчёта выберите известные параметры, по которым будут произведены расчёты, за тем введите их и нажмите кнопку «Рассчитать».
Если Вам необходим узнать по каким формулам ведется расчет для фигуры, а так же задать единицы измерения или сохранить расчет в PDF, то воспользуйтесь сайтом calc-online24.ru
Вычисление диаметра трубы по хорде
Бывают ситуации, когда необходимо измерить диаметр чего-либо, например, трубопровода, но нет возможности измерить длину окружности (из-за изоляции или температуры).
В этом случае можно применить метод вычисления диаметра по хорде. Для этого метода необходим только штангенциркуль.
- Прикладываем его, как показано на рис. 1;
- измеряем длину L;
- измеряем высоту губок штангенциркуля Н;
- вычисляем диаметр по формуле D = (L 2 ⁄ 4H) + H или
- вычисляем радиус по формуле r = (L 2 + 4H 2 ) ⁄ 8H
Рисунок 1
Если под рукой только «штангель» с длинными губками или не хватает его измеряемого диапазона можно применить какую-нибудь «проставку». В идеале подойдёт плоскопараллельная концевая мера… 😉 Её надо вставить, как показано на рисунке 2, и при вычислении, от длины губок отнять высоту этой «проставки». Н = Н1 — Н2
Рисунок 2
Точность этого метода зависит, только от инструмента, который Вы будете применять.
Длина хорды и высота сегмента круга
Зная длину хорды и высоту сегмента круга, необходимо для вычисления всех остальных параметров воспользоваться одновременно обеими формулами, выразив через них радиус круга. c=2r sin〖α/2〗 h=r(1-cos〖α/2〗 ) r=h/2+c^2/8h
Угол сегмента круга можно выразить через любую из вышеприведенных формул для хорды и высоты сегмента. В случае с хордой синус половинного угла будет равен ее длине, деленной на два радиуса. sin〖α/2〗=c/2r
Длина дуги и площадь сегмента круга вычисляются по стандартным формулам, в которые необходимо подставить полученное для радиуса выражение. P=αr=α(h/2+c^2/8h) S=r^2 (α/2-sinα )=1/2 (h/2+c^2/8h)^2 (α-sinα )
Как найти с помощью хорды диаметр окружности?
NERO
Знаток
(343),
закрыт
14 лет назад
Айрат Саттаров
Оракул
(99057)
14 лет назад
Зная только длину хорды, диаметр найти невозможно! Надо знать еще угол между радиусами, отсекающими эту хорду. Если он известен, то решай равнобедренный треугольник с основанием – хордой и двуми сторонами, равными радиусами с вершиной в центре окружности.
|
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Радиус окружности с длиной хорды окружности связан формулой:
Здесь R – радиус L – длина хорды, a – центральный угол. Далее я покажу построения для расчёта радиуса:
Найдём радиус из прямоугольного треугольника OKB. Здесь KB=L/2=72/2=36. Далее по теореме Пифагора получается: OB=sqrt(OK^2+KB^2)=sqrt(27^2+36^2)=45.Радиус окружности: R=OB=45 единиц. Диаметр окружности: D=2*R=2*45-90 единиц. Ответ: диаметр окружности D=90 единиц. автор вопроса выбрал этот ответ лучшим
Радиус окружности можно высчитать, как гипотенузу прямоугольного треугольника, где один катет, это половина длины хорды, а другой катет – это расстояние от центра окружности до хорды: sqr((72/2)² + 27²) = 45 единиц, а если радиус составляет 45 единиц, диаметр тогда будет равен 90 единиц. Знаете ответ? |
Деление окружности на любое количество равных частей
Деление окружности на любое количество равных частей
Окружность является одним из основных элементов изонити и на ней нужно разметить большое количество точек проколов. Как это сделать? Об этом сегодняшний пост.
Для деления окружности на любое количество равных частей можно воспользоваться коэффициентами (см. таблицу 1.). Зная на какое число n следует разделить окружность, находят коэффициент k. При умножении коэффициента k на диаметр D этой окружности, получают длину хорды, которую циркулем откладывают на заданной окружности n раз.
|
n |
k |
n |
k |
| 3 | 0,86603 | 20 | 0,15643 |
| 4 | 0,70711 | 21 | 0,14904 |
| 5 | 0,58779 | 22 | 0,14231 |
| 6 | 0,5 | 23 | 0,13617 |
| 7 | 0,43388 | 24 | 0,13053 |
| 8 | 0,38268 | 25 | 0,12533 |
| 9 | 0,34202 | 26 | 0,12054 |
| 10 | 0,30902 | 27 | 0,11609 |
| 11 | 0,28173 | 28 | 0,11196 |
| 12 | 0,25782 | 29 | 0,10812 |
| 13 | 0,23932 | 30 | 0,10453 |
| 14 | 0,22252 | 31 | 0,10117 |
| 15 | 0,20791 | 32 | 0,09802 |
| 16 | 0,19509 | 33 | 0,09506 |
| 17 | 0,18375 | 34 | 0,09227 |
| 18 | 0,17365 | 35 | 0,08964 |
| 19 | 0,16459 | 36 | 0,08716 |
Если требуется большее количество, то коэффициент можно рассчитать самостоятельно. Для этого делим 360 на нужное количество частей и берем синус этого числа. Полученный результат делим на два — это и есть наш коэффициент.
Понятно, что все вышеописанное применимо только к правильной, “круглой” окружности, а не к любому замкнутому контуру, который также прошивается по правилу заполнения окружности. И только если нужно получить на контуре окружности равные отрезки. Иначе все придется делать вручную, без применения математики и прочих геометрических построений.
Популярные сообщения из этого блога
Перепись населения — Опрос
В декабре, через пару недель, блогу исполняется год. Страшно подумать – уже целый год! Когда я начинал писать в блог, у меня в запасе хорошо если набралось десяток тем будущих постов, а написанных постов в черновиках не было и вовсе, что, с точки зрения серъезного блоггинга, никуда не годилось.
Получилось, я действовал по принципу – Сначала ввяжемся, а потом посмотрим. И вот что получилось. На сегодняшний день моя читательская аудитория представлена 58 странами. Но мне очень хотелось бы узнать больше о том, кто приходит ко мне в блог и с какой целью, как используюся материалы блога. Это очень важно, чтобы я мог оценить полезность наполнения страниц и в будущем году, на новом витке развития, учесть пожелания уважаемой аудитории (во загнулJ). Я разработал опросник, состоящий из 10 вопросов с мульти-выбором, т.е. нужно выбрать один из предлагаемых ответов. Если есть что-то, что Вам хотелось бы высказать, но это не вошло в список вопросов, пишите мне на e-mail или в комментриях к этому
Далее…
Материалы для работы в технике “изонить”. Часть 2: Нитки
В предыдущем посте мы рассматривали что можно использовать как фон для картинки, вышитой изонитью. Сегодня рассмотрим какие нитки лучше брать. Правильно подобранные нитки являются основой восприятия картины.
Вышивать можно любыми не очень толстыми нитками. Работы выглядят лучше, если вышиты блестящими нитками, а не матовыми. Лучше вышивать кручеными нитями, чем в несколько рассыпающихся нитей. Например, сердцевина ромашки (смотри ниже) вышита металлизированной нитью. В исходной нити было 9 ниточек, Я вышивал, беря по 3. Оказалось очень неудобно. Наиболее часто используется мулине, поскольку с ним работать наиболее легко. Хорошие нити мулине должны обладать блеском и иметь равномерную прокраску. Обычно мулине поступает в продажу пасмами, состоящими из 6 ниточек. Если ниточки разделить, то каждая из них должна быть ровной по толщине и не должна лохматиться. (Я предпочитаю разделять пасма на отдельные ниточки и вышивать по одной. Пробовал брать больше ниток – работа выглядела грубов
Далее…
Математическая задача: Хорда окружности — вопрос № 972, алгебра, квадратное уравнение
Определите радиус окружности, в которой хорда, удаленная от центра на 6 см, на 12 см длиннее радиуса окружности.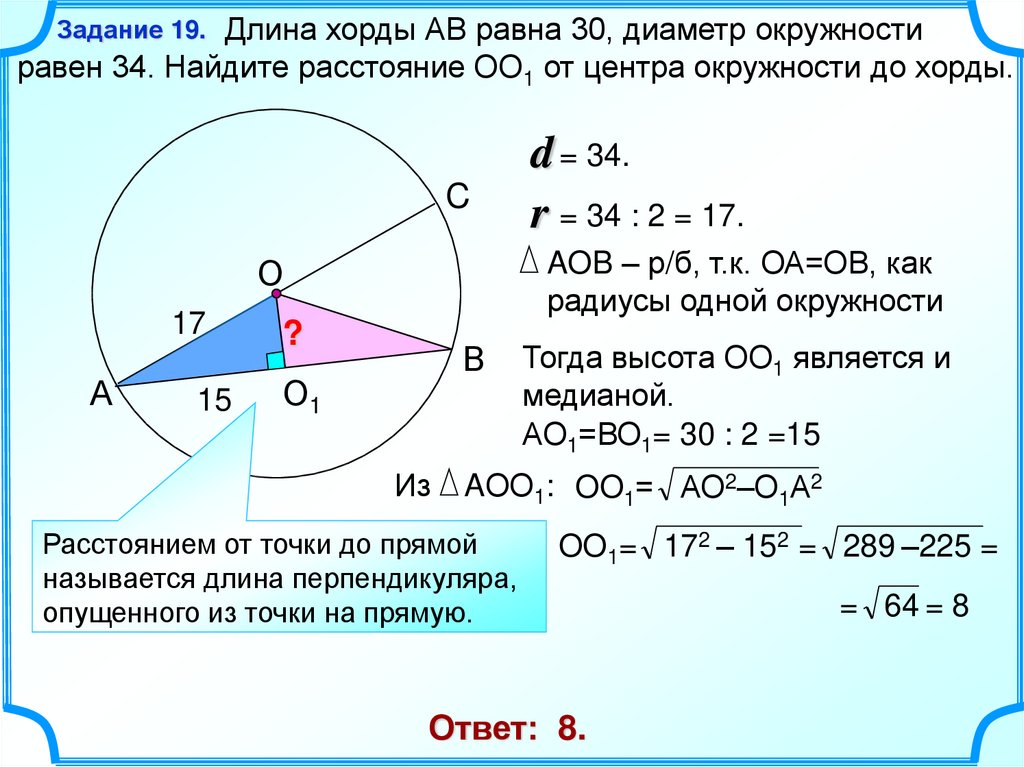
Правильный ответ:
r = 14,58 см
Пошаговое объяснение:
r2=62+(2r+12)2 3r2−24r−288=0 a=3;b=−24;c =−288 D=b2−4ac=242−4⋅3⋅(−288)=4032 D>0 r1,2=2a−b±D
=624±4032
=624±247
r1,2=4±10,583005 r1=14,583005244 r2=−6,583005244 Факторизованная форма уравнения: 3(r−14,583005244)(r+6,583005244)=0 r=9,5 r=9,5 r=9,8 r0003
Нашли ошибку или неточность? Не стесняйтесь
пишите нам
. Спасибо!
Советы для связанных онлайн-калькуляторов
Вам нужна помощь в вычислении корней квадратного уравнения?
Теорема Пифагора является основой для калькулятора прямоугольного треугольника.
Для решения этой задачи по математике вам необходимо знать следующие знания:
- алгебра
- квадратное уравнение
- Неравенство
- Planimetrics
- Pythagorean Теорема
- Circle
- Аккорд
Оценка слов Проблема:
- СРЕДНА
9002.
video1 video2
- Вычислить 2577
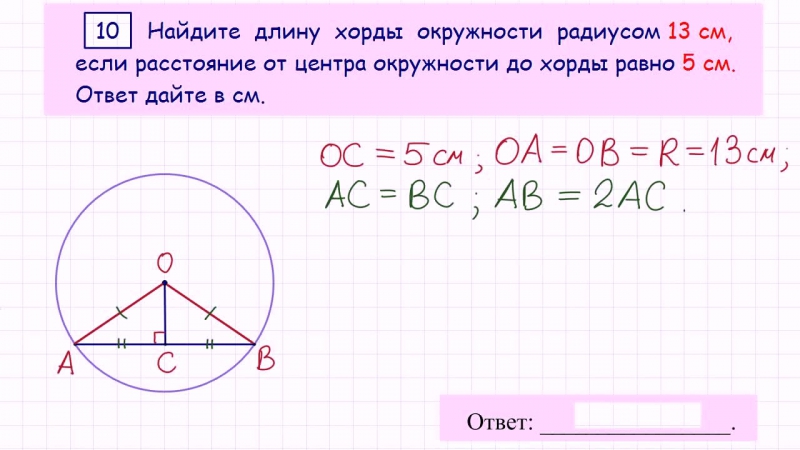
Вычислить длину хорды окружности, которая находится на расстоянии 2,5 см от центра окружности. Радиус 6,5 см. - Хорда окружности
Вычислите длину хорды окружности радиусом r = 10 см, длина которой равна расстоянию от центра окружности. - Хорды круга
Хорды круга имеют две длины: 30 и 34 см. Более короткая хорда идет от центра в два раза длиннее хорды. Определить радиус окружности. - Хорда 3
Хорда составляет 2/3 радиуса окружности от центра и имеет длину 10 см. Какова длина радиуса окружности? - Хорда
В окружности радиусом r=60 см проходит хорда, длина которой в 4 раза больше ее расстояния от центра. Какова длина хорды? - Рассчитать 79144
Радиус окружности r=8,9 см, хорда AB этой окружности имеет длину 16 см. Вычислите расстояние хорды АВ от центра окружности. - Хорда
Рассчитайте длину хорды, если расстояние от центра окружности (S, 6 см) равно 3 см.
- Хорда 2
Точка А находится на расстоянии 13 см от центра окружности с радиусом r = 5 см. Вычислите длину хорды, соединяющей точки Т1 и Т2 касательных, проведенных из точки А к окружности. - Вычислить 3562
Нить длиной 16 см проходит на расстоянии 6 см от центра круга. Вычислите длину окружности. - Хорда MN
Хорда MN окружности на расстоянии от центра окружности S 120 см. Угол MSN равен 64°. Определить радиус окружности. - Хорда 5
Дан круг к/с; 5 см/. Его хорда MN находится на расстоянии 3 см от центра окружности. Вычислите его длину. - Концентрические окружности и хорда
В окружности диаметром d = 10 см построена хорда длиной 6 см. Какой радиус имеет концентрическая окружность при касании этой хорды? - Два кольца
Площадь кольцевой окружности, образованной двумя окружностями с общим центром, составляет 100 см². Радиус внешней окружности равен удвоенному радиусу внутренней окружности. Определить радиус внешней окружности в сантиметрах. - Вычислить 3561
В окружности есть хорда длиной 12 см и радиусом 10 см. Вычислите расстояние хорды от центра окружности. - Две хорды
Рассчитайте длину хорды AB и хорды, перпендикулярной BC к окружности, если AB находится на расстоянии 4 см от центра окружности, а BC — на 8 см от центра. - Две хорды
Дана окружность k (центр S, радиус r). Из точки А, лежащей на окружности k, начинаются две хорды длины r. Какой угол составляют хорды? Нарисуй и измерь. - Хорда
В окружности радиусом 6 см проведена хорда на расстоянии 3 см от центра. Вычислите угол, образуемый шнуром в центре окружности. Отсюда найдите длину малой дуги, отсекаемой хордой.
Вычислите длину хорды, проходящей на расстоянии 6 см от центра окружности диам…
Перейти к
- Круговое упражнение 15.1
-
Круговое упражнение 15. 2
2
- Рациональные и иррациональные числа
- Сложные проценты
- Расширения
- Факторизация
- Одновременные линейные уравнения
-
Задачи на одновременные линейные уравнения
- Квадратные уравнения
- Индексы
- Логарифмы
- Треугольники
- Теорема о средней точке
-
Теорема Пифагора
- Прямолинейные фигуры
- Теоремы о площади
- Круг
- Измерение
- Тригонометрические отношения
-
Тригонометрические отношения и стандартные углы
- Координатная геометрия
- Статистика
Главная >
ML Aggarwal Solutions
Класс 9
Математика
>
Глава 15 — Круг
>
Круговое упражнение 15.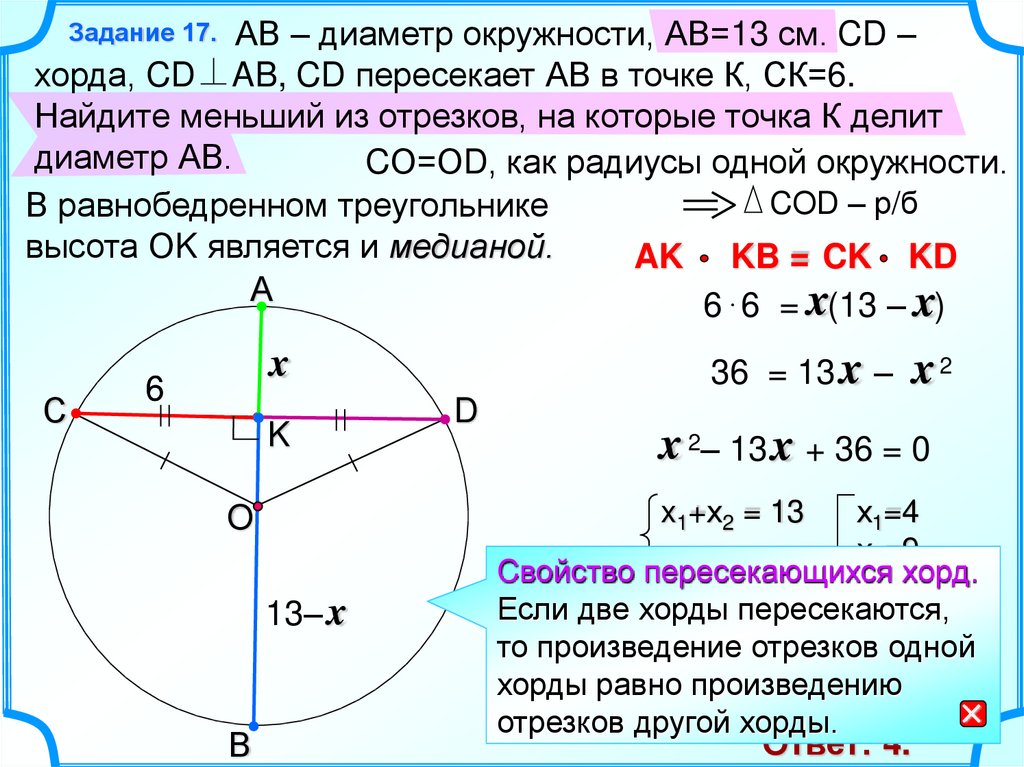
{2}
end{выровнено}
AM = 8 см
OM ⊥ AB
M — середина AB.
АВ = 2 АМ = 2 × 8 = 16 см.
Стенограмма видео
«Здравствуйте и добро пожаловать, мои дорогие студенты
Я Ришаб, репетитор по математике на Лидо
и я здесь новый вопрос он говорит
рассчитать длину кода, который
находится на расстоянии
6 см от центра
круг
для диаметра 20 см так без
потеряем много времени давайте посмотрим на
решение
поэтому нам дали этот аккорд abc
тогда как oa — радиус
а также из рисунка замечаем, что
om перпендикулярен a b
теперь, поскольку нам известно, что диаметр
20
поэтому я пишу d для диаметра
быть 20 сантиметров
что означает, что радиус r
не что иное, как 20 на 2, что равно 10
сантиметр
разделит этот сегмент
так что мы наблюдаем сейчас
что oa составляет 10 сантиметров
ома6
теперь в прямоугольном треугольнике
4 утра, будь осторожен, мой ученик, это стоит rt
за право
так что это читается как прямоугольный треугольник
мы видим, что квадрат oa равен
ом квадрат
плюс я квадратный
o дается на 10 больше
м равно 6
и сейчас я квадратный
упрощая его, мы получаем am квадрат
равно
100 минус 36, что равно 64.
значит am равен 8 сантиметрам
будьте осторожны, что мы обязаны найти
длина
шнур
это означает
у нас есть до сих пор
имея в виду, что ом
перпендикулярно а б
мы замечаем, что m является серединой a b
что означает, что a b в два раза больше
я что значит
2 в 8, что равно 16
сантиметр
значит a b равно 16 сантиметрам
Я надеюсь, что мои ученики получили этот вопрос
ну не забудь подписаться
кнопка
Вы также можете поделиться своими сомнениями в
раздел комментариев, увидимся в следующий раз, пока»
Связанные вопросы
Вычислите длину хорды, которая находится на расстоянии 12 см от центра окружности радиуса…
Хорда длиной 8 см проходит на расстоянии 3 см от центра окружности. Вычислите радиус…
Хорда длиной 16 см проходит на расстоянии 6 см от центра окружности. Найдите длину т…
В окружности радиусом 5 см AB и CD проходят две параллельные хорды длиной 8 см и 6 см соответственно.
