Цель работы:
Научиться выполнять измерения способом рядов.
Приборы и материалы:
Линейка, дробь (или горох), иголка.
Указания к работе:
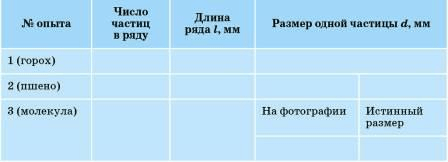
1. Положите вплотную к линейке несколько (20−25 штук) дробинок (или горошин) в ряд. Измерьте длину ряда и вычислите диаметр одной дробинки.
2. Определите таким же способом размер крупинки пшена (или зёрнышка мака). Чтобы удобнее было укладывать и пересчитывать крупинки, воспользуйтесь иголкой. Способ, которым вы определили размер тела, называют способом рядов.
3. Определите способом рядов диаметр молекулы по фотографии (рис. 199, увеличение равно 70 000).
4. Данные всех опытов и полученные результаты занесите в таблицу 7.

рис. 199.
Таблица 7.

reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. №2 Измерение размеров малых тел. Номер №1
Решение
Измерить размер малых тел, например пшеничное зерно, с помощью линейки невозможно. Это связано с тем, что размер пшена соизмеримы с размером цены деления линейки (обычно 1 мм), а зачастую даже меньше. Для таких измерений требуются приборы с меньшей ценой деления, то есть с большей точностью измерения. Несмотря на это, имея пару десятков зёрнышек, можно измерить средний размер (диаметр) этих зёрен с помощью линейки.
Чтобы измерить размер малых тел, например дробинок или горошин, нужно выложить, начиная от нулевого деления линейки, малые тела в ряд вплотную друг к другу вдоль шкалы линейки. Средний диаметр зерна будет равен длине, разделённой на количество зёрнышек.
Чтобы удобнее было укладывать и пересчитывать крупинки, воспользуемся иголкой.
Вычисления:
D
=
l
n
, где D − диаметр зерна, l − длина ряда, n− количество зёрен.
1) пшено.
D
=
28
24
=
1
,
17
мм;
2) горох.
D
=
43
21
=
2
,
05
мм.
3) молекула (на фотографии)
D
=
25
14
=
1
,
79
мм.
молекула (истинный размер)
D
=
25
14
∗
70000
=
0
,
0000255
мм или
2
,
55
∗
10
−
5
мм.
| № опыта | Число частиц в ряду | Длина ряда l,мм | Размер одной частицы d,мм |
|---|---|---|---|
| 1. Горох | 21 | 43 | 2,05 |
| 2. Пшено | 24 | 28 | 1,17 |
| 3. Молекула, на фотографии | 14 | 25 | 1,79 |
| Молекула, истинный размер | 2 , 55 ∗ 10 − |
Вывод. В ходе лабораторной работы мы научились выполнять измерения малых тел способом рядов.
Определение размеров молекул
1 способ. Основан на том, что молекулы вещества, когда оно находится в твердом или жидком состоянии, можно считать плотно прилегающими друг к другу. В таком случае для грубой оценки можно считать, что объем V некоторой массы m вещества просто равен сумме объемов содержащихся в нем молекул. Тогда объем одной молекулы мы получим, разделив объем V на число молекул N.
Число молекул в теле массой m равно, как известно,  ,
,
где М — молярная масса вещества NA — число Авогадро.
Отсюда объем V0 одной молекулы определяется из равенства 
В это выражение входит отношение объема вещества к его массе.
Обратное же отношение 
есть плотность вещества,
так что 
Плотность практически любого вещества можно найти в доступных всем таблицах. Молярную массу легко определить, если известна химическая формула вещества.
Объем одной молекулы, если считать ее шариком, равен  ,
,
где r – радиус шарика.
Поэтому  ,
,
откуда мы и получаем выражение для радиуса молекулы:

Первый из этих двух корней — постоянная величина, равная ≈ 7,4 · 10-9 моль 1/3, поэтому формула для r принимает вид  .
.
Например, радиус молекулы воды, вычисленный по этой формуле, равен rВ ≈ 1,9 · 10-10 м.
Описанный способ определения радиусов молекул не может быть точным уже потому, что шарики нельзя уложить так, чтобы между ними не было промежутков, даже если они соприкасаются друг с другом. Кроме того, при такой «упаковке» молекул – шариков были бы невозможны молекулярные движения. Тем не менее, вычисления размеров молекул по формуле, приведенной выше, дают результаты, почти совпадающие с результатами других методов, несравненно более точных.
2 способ. Метод Ленгмюра и Дево. В данном методе исследуемая жидкость должна растворяться в спирте (эфире) и быть легче воды, не растворяясь в ней. При попадании капли раствора на поверхность воды спирт растворяется в воде, а исследуемая жидкость образует пятно площадью S и толщиной d (порядка диаметра молекул).
Если допустить, что молекула имеет форму шара, то объем одной молекулы равен:
 где d – молекулы.
где d – молекулы.
Необходимо определить диаметр молекулы d. В микропипетку набрать 0,5 мл раствора и, расположив ее над сосудом, отсчитать число капель n, содержащихся в этом объеме. Проделав опыт несколько раз, найти среднее значение числа капель в объеме 0,5 мл, а затем подсчитать объём исследуемой жидкости в капле:  , где n – число капель в объеме 0,5 мл, 1:400 – концентрация раствора.
, где n – число капель в объеме 0,5 мл, 1:400 – концентрация раствора.
В ванну налить воду толщиной 1 – 2 см. Насыпать тальк тонким слоем на лист бумаги, ударяя слегка пальцем по коробочке. Расположив лист бумаги выше и сбоку от ванны на расстоянии 10 – 20 см, тальк сдуть с бумаги. На поверхность воды в ванне из пипетки капнуть одну каплю раствора. Линейкой измерить, средний диаметр образовавшегося пятна D и подсчитываю его площадь. Опыт повторить 2- 3 раза, а затем подсчитать диаметр молекул d.
3 способ. Определение диаметра молекулы. Будем считать, что капля масла растекается по воде до тех пор, пока толщина масляной плёнки не станет равной одной молекуле, тогда диаметр одной молекулы можно определить по формуле: d=V/S, где V – объём капли масла, S – площадь масленого пятна.
Объём капли масла можно определить следующим образом: накапать 100 капель из капилляра в сосуд и измерить массу масла в нём. После этого массу, выраженную в килограммах, поделить на плотность масла, которую можно взять из таблицы плотности некоторых веществ (плотность масла растительного 800 кг/м3).
Затем полученный результат поделить на количество капель. Объём капли можно определить также с помощью мерного цилиндра: накапать масло в цилиндр, измерить его объём в см3 и перевести в м3, для чего поделить на 1000000, затем на количество капель масла. После того, как объём капли стал известен нужно капнуть одну каплю масла на поверхность воды, которая налита в широкий сосуд.
Для ускорения реакции предварительно немного нужно нагреть воду – приблизительно до 400С. Масло начнёт растекаться, и в результате получится круглое пятно. После того, как пятно перестанет расширяться, с помощью линейки измерить его диаметр и рассчитать площадь пятна по формуле: 
Практическое получение наночастиц
В современном мире в связи с общей тенденцией к миниатюризации большими темпами стала развиваться такая наука, как нанотехнология. Методы нанотехнологии позволяют получить принципиально новые устройства и материалы с характеристиками, значительно превосходящими их современный уровень, что весьма важно для интенсивного развития многих областей техники, биотехнологии, медицины, охраны окружающей среды и др.
Ход работы:
1) Определение объёма капли
 =14,13 мм3;
=14,13 мм3;
2) Определение объёма капли путём взвешивания.
1. На весы накапали 10 капель растительного масла, измерили массу
mk=0,2 г
- Масса 1 капли m1=0,2 г/10=0,02 г
- Определение объёма капли V=m1/q=0,01г/0,8 г/см3=13 мм3
3) Определяем площадь пятна Sмасла=ПR2=11304 мм2
(Приложение 1,2,3,4,5)
4) Площадь пятна нефти Sнефти=20*16=32000 мм2
(Приложение 6,7,8,9)
5) Определяем толщину плёнки h=V/S
Для масла h=13/11304=1,2*10-7=120 нм
Для нефтиh=13/32000=4*10-8 м=40 нм
Вывод: В лабораторных условиях можно получать нанопленки
Заключение
Мы измерили толщину наноплёнок масла и нефти, изучили физические свойства плёнок и методы их получения, также ознакомились с физическими методами исследования микро- и наномасшатабных объектов.
К сожалению, из таких жидкостей как кислоты(уксусная, ортофосфорная, борная), моющие средства и мыло у нас не получилось сделать наноплёнки, потому что все эти жидкости гидрофобные(боятся воды).Мы пытались получить пленки с помощью скотча, но электронные весы позволяют измерять массу с точностью до десятых долей грамма
Список использованной литературы
- Анциферов Л.И. Самодельные приборы для физического практикума в средней школе. М.: Просвещение, 1985.
- Блудов М.И. Беседы по физике. М.: Просвещение, 1984.
- Буров В.А. Практикум по физике в средней школе. М.: Просвещение, 1973.
Приложения


как найти размер одной частицы. гороха и пшена в мм
Конструктор смерти
Ученик
(107),
закрыт
11 лет назад
ДамирАльмухаметов
Знаток
(354)
11 лет назад
возьми горох и запихни в спичечный коробок, по максимуму!!! Потом найди объем этого короба, потом разделишь объем на количество гороха, которое поместилось в короб. Это ты найдешь приблизительный объем 1 гороха, а диаметр найдешь из этой формулы -( пи*(диаметр) в кубе) /6

где fsi ni di2 / nidi2 – поверхностная доля i-ой фракции.
i
Среднемассовый (или среднеобъемный) диаметр dw соответствует диамет-
ру частиц в такой монодисперсной системе, в которой суммарная масса (или объем) частиц такие же, как и в данной полидисперсной системе:
|
n d 3 |
|||||||||||
|
dw |
fwi di , |
(11) |
|||||||||
|
3 di |
|||||||||||
|
i i |
|||||||||||
|
i |
ni di |
i |
|||||||||
|
i |
|||||||||||
|
где fwi ni di3 / nidi3 – массовая (объемная) доля i-ой фракции. |
|||||||||||
|
i |
|||||||||||
|
Среднемассовый диаметр частиц рассчитывают, например, по данным се- |
|||||||||||
|
диментационного анализа. Значения dw |
могут быть найдены также методами |
||||||||||
|
ситового анализа и рассеяния света. Среднеповерхностный диаметр ds |
опреде- |
ляют, изучая адсорбцию на частицах дисперсной фазы. Среднечисленный диаметр dn , чаще всего, находят методами оптической и электронной микроскопии.
Усредненные размеры частиц dn , ds и dw одинаковы лишь для монодис-
персных систем, а в полидисперсных системах они различны. При этом всегда dw > ds > dn и чем более полидисперсна система, тем в большей степени разли-
чаются их значения. Поэтому степень полидисперсности систем часто характе-
|
ризуют параметром: |
||||||
|
П = |
d |
n |
. |
(12) |
||
|
dw |
Очевидно, что для монодисперсных систем П = 1, а для полидисперсных систем П 1.
В отсутствии данных о средних размерах частиц, найденных с использованием разных методов усреднения, для характеристики степени полидисперсности исследуемой системы может использоваться коэффициент вариации:
|
Kn |
100%, |
(13) |
||
|
d n |
||||
где – стандартное отклонение, которое характеризует широту распределения частиц по размерам.
Стандартное отклонение может быть определено на основе тех же исходных данных, что и средний размер частиц. Например, стандартное отклонение для среднечисленного диаметра рассчитывается по следующему соотношению:
|
1/ 2 |
1/ 2 |
||||||||||||||
|
n |
2 |
2 |
|||||||||||||
|
i |
di dn |
fni di |
dn |
. |
(14) |
||||||||||
|
ni |
|||||||||||||||
|
i |
i |
||||||||||||||
|
i |
Обычно система рассматривается как монодисперсная, если коэффициент вариации составляет менее 5 % (или, как максимум, 10 %).
13
2. ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ИХ ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
Помимо наибольшего, наименьшего и среднего размеров частиц более полно полидисперсность материала характеризуется дисперсным (гранулометрическим, зерновым) составом. Данная характеристика позволяет определить не только перечисленные параметры, но и установить процентное содержание частиц с определенным интервалом размеров.
С точки зрения математической статистики, диаметр частиц можно рассматривать как одномерную случайную величину. В этом случае свойства полидисперсного материала описывают функцией распределения числа (массы, площади и пр.) частиц от их размера.
Как правило, процентное содержание отдельных фракций представляют в виде гистограммы – ступенчатого графика зависимости относительного содержания фракций частиц от их размера.
Гистограмму строят в виде диаграммы, состоящей из нескольких прямоугольников (их число соответствует числу фракций), основания которых находятся между значениями диаметра от di– di/2 до di+ di/2 (рис. 4). Такие гистограммы дают наглядное представление о степени полидисперсности анализируемых систем и содержании в них каждой фракции, поскольку интервалы диаметров во фракциях берутся одинаковыми.
При построении дифференциальных кривых распределения частиц по размерам по оси абсцисс также отсчитываются значения их диаметров, а по оси ординат – отношение процентного содержания частиц в каком-то интервале размеров Qi к этому интервалу di, т.е. плотность распределения. Здесь величины интервалов размеров di могут быть неодинаковыми. Дифференциальную кривую распределения частиц по размерам получают, построив на графике отдельные для каждого интервала от di– di/2 до di+ di/2 прямоугольники и соединив средние точки их верхних оснований плавной кривой (рис. 5).
Для получения дифференциальной кривой численного распределения по оси ординат откладывают отношения Qni/ di. Значение численного содержания каждой фракции в процентах вычисляют по формуле:
|
Qni |
ni |
100 fni |
100. |
(15) |
|
|
ni |
|||||
i
Для построения дифференциальных кривых массового и поверхностного распределения по размерам по оси ординат наносят, соответственно, Qwi/ di иQsi/ di. Значения массового и поверхностного содержания фракций в процентах рассчитывают как
|
Qwi |
n d |
3 |
100 fwi |
100; |
||
|
i |
i |
|||||
|
ni di3 |
||||||
|
i |
||||||
|
Qsi |
n d 2 |
100 fsi |
100. |
|||
|
i |
i |
|||||
|
ni di2 |
i
14

Рис. 4. Гистограмма распределения частиц по размерам
Рис. 5 Дифференциальная кривая распределения частиц по размерам
Дифференциальные кривые численного, поверхностного и массового распределения частиц по размерам для одной и той же полидисперсной системы имеют вид, показанный на рис 6. С уменьшением степени полидисперсности
15

систем ширина дифференциальных кривых распределения становится уже, а их максимум увеличивается.
В пределе, при бесконечном числе фракций, имеем:
|
Q |
dQ |
F di , |
(18) |
|||
|
lim |
i |
|||||
|
di 0 |
di |
dd |
где F(di) – функция распределения (а точнее, численное значение функции распределения в i-ой точке).
Рис. 6. Дифференциальные кривые численного (1), поверхностного (2) и массового (3) распределения частиц по размерам
В соответствии со свойствами функции распределения можем записать:
|
dfi F di ddi |
(19) |
|
|
и |
||
|
d2 |
||
|
f12 F di |
ddi , |
(20) |
|
d1 |
||
|
где dfi – доля частиц (в процентах) с размерами от di до di ddi ; |
f12 – доля час- |
|
|
тиц (в процентах) с размерами от d1 до d2 . |
Графически эта доля частиц f12 равна площади под кривой функции распределения, ограниченной с двух сторон диаметрами d1 и d2
16

F d
3. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ОПИСАНИЯ ДИСПЕРСНОГО СОСТАВА
Для полного описания дифференциальной кривой и расчета основных параметров распределения удобнее использовать непрерывную функцию распределения в аналитическом виде. Были предложены различные функции
F d для описания дифференциальных кривых распределения, получаемых
при дисперсионном анализе реальных систем. Вид кривых распределения может быть различным в зависимости от физико-химических свойств порошка и, в основном, от способа его получения.
Для аналитического описания кривых распределения существуют различные формулы. Используемые формулы могут быть одно-, двух- и трех параметрическими и подразделяются на теоретические и эмпирические. Теоретические формулы выведены на основе некоторых физических представлений о закономерностях распределения частиц дисперсных материалов. Эмпирические получены на основе описания экспериментальных результатов дисперсионного анализа.
Среди теоретических наиболее часто используется нормальное (распределение Гаусса) и логарифмическое нормальное (логнормальное) распределения.
Принимая общее содержание частиц за 100%, уравнение нормального распределения может быть записано как
|
2 |
|||||||||||||
|
100 |
1 |
d d |
|||||||||||
|
FG d |
(21) |
||||||||||||
|
exp |
, |
||||||||||||
|
2 |
2 |
||||||||||||
где d – средний диаметр частиц, величина которого, как это отмечалось ранее, зависит от метода усреднения; – стандартное отклонение распределения вокруг среднего.
Для построения кумулятивной (интегральной) кривой распределения уравнение (21) должно быть проинтегрировано:
|
di |
2 |
ti |
2 |
||||||||||||||||||||
|
100 |
1 |
d d |
100 |
t |
|||||||||||||||||||
|
Q d di |
(22) |
||||||||||||||||||||||
|
exp |
dd |
exp |
dt, |
||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||
|
/ ; Q d di |
– доля частиц (в процентах) с размерами от до di . |
||||||||||||||||||||||
|
где t d d |
Для расчета доли частиц Q d di интегрирование должно быть проведено в пределах от di до .
Логарифмическое нормальное распределение получается, если в нормальную Гауссову функцию распределения подставить в качестве аргумента не диаметр частиц, а логарифм диаметра. В таком случае функция F имеет вид:
|
2 |
||||||||||||||||
|
100 |
1 |
ln d ln dg |
||||||||||||||
|
FL ln d |
||||||||||||||||
|
exp |
, |
(23) |
||||||||||||||
|
d ln g 2 |
2 |
ln g |
||||||||||||||
|
где g – |
геометрическое стандартное отклонение (логарифм величины g ра- |
|||||||||||||||
|
17 |

d de
вен стандартному отклонению величины ln d ); dg – средний геометрический
диаметр частиц, логарифм которого равен значению среднего логарифма диаметров ln dg ln d .
Следует отметить, что применимость того или иного распределения для описания состава конкретной дисперсной системы определяется главным образом способом получения этой системы. Так, в частности, распределение частиц по размерам, получаемых помолом, очень близко к логарифмически нормальному.
Из эмпирических уравнений распределения часто используются формулы Годена и Розина–Раммлера [3].
Формула Годена, выведенная на основе обобщения результатов ситового анализа минералов, измельченных различными методами, имеет вид:
где dmin – минимальный диаметр для данной фракции частиц (нижняя граница диапазона диаметров частиц данной фракции), А и l – константы уравнения.
Из формулы (24) следует, что она не предназначена для описания интегральных кривых распределения частиц по размерам, у которых есть точка перегиба, соответствующая, например, максимуму на дифференциальной кривой распределения. Это означает, что она может быть использована для описания только какой-то части полной интегральной кривой распределения.
Для описания интегральных кривых распределения по данным ситовых анализов может быть использована формула Розина–Раммлера:
|
d |
a |
|||||
|
Q 100 exp |
, |
|||||
|
(25) |
||||||
|
de |
||||||
где a – постоянная этого уравнения, характеризующая ширину распределения, de – такой диаметр, при котором масса частиц с диаметрами составляет
36,8 %.
Следует отметить, что как формула Годена, так и Розина–Раммлера в основном хорошо описывают характеристики порошков, полученных измельчением с помощью определенного оборудования [3]. Так, например, было установлено, что формула Годена описывает данные для порощков, полученных при использовании валковых и щековых дробилок, а также стержневой мельницы. Те же самые материалы, но измельченные в шаровой мельнице, описывались данным уравнением лишь в ограниченном интервале размеров.
18
4. ОПТИЧЕСКАЯ МИКРОСКОПИЯ
Оптический или световой микроскоп представляет собой оптическую систему с двумя ступенями увеличения – объективом и окуляром. Объектив представляет собой первую ступень увеличения.
Принципиальная схема микроскопа приведена на рис. 7. Объект освещается источником света через оптическую систему коллектор-конденсор. Конденсор представляет собой короткофокусную линзу или систему линз, используемую в оптическом приборе для освещения рассматриваемого или проецируемого предмета. Конденсор собирает, усиливает и превращает поток света в пучок равномерных параллельных лучей в границах всей площади конденсора, который рассчитывается для освещения площади исследуемого предмета. Конденсор направляет на предмет лучи от источника света, в том числе и такие, которые в его отсутствие проходят сквозь предмет. В результате такого уплотнения светового потока резко возрастает освещенность предмета. Объектив создает действительное перевернутое и увеличенное изображение объекта, которое рассматривается через окуляр. Окуляр предназначен для создания дополнительного увеличения и создает мнимое изображение [3].
Существует большое количество разнообразных объективов, их классификация основана на степени исправления оптических искажений – хроматических и сферических аберраций. Хроматические аберрации обусловлены тем, что световые волны с разной длиной фокусируются в разных точках на оптической оси. В результате изображение оказывается окрашенным. Сферические аберрации связаны с тем, что свет, проходящий через центр объектива, и свет, идущий через его периферийную часть, фокусируются в разных точках на оси. В результате изображение оказывается нечетким. Ахроматические объективы являются наиболее распространенными на данный момент. В них хроматические аберрации подавляются при помощи стеклянных элементов с разной дисперсией, обеспечивающих схождение крайних лучей видимого спектра – синих и красных – в одном фокусе. Небольшая окрашенность изображения остается и видна иногда в виде слабых зеленых полос вокруг объекта. Сферическая аберрация может быть скорректирована только для одного цвета. Во флюоритовых объективах при помощи добавок к стеклу, улучшающих цветовую коррекцию, окрашенность изображения почти полностью устраняется. Апохроматические объективы – это объективы с самой сложной цветовой коррекцией. В них не только почти полностью устранены хроматические аберрации, но и коррекция сферических аберраций выполнена не для одного, а для двух цветов.
Общее увеличение микроскопа определяется как произведение увеличения объектива на увеличение окуляра. Наиболее распространены объективы с увеличением от 3Х до 90Х и окуляры от 5Х до 20Х, таким образом, общее увеличение микроскопа в видимой области спектра можно изменять в пределах от 15Х до 1800Х. Разрешающая способность оптического микроскопа составляет порядка 0,2–0,3 мкм.
19

Рис. 7. Схематичное изображение оптического микроскопа: окуляр (1), объектив (2), исследуемый объект (3), конденсор (4), предметный столик (5), осветительное зеркало (6) [4]
Для наблюдения частиц меньших размеров необходимо увеличить разрешающую способность микроскопа. Это возможно осуществить двумя способами: применяя свет с меньшей длиной волны и увеличивая апертуру объектива. Апертура представляет собой действующее отверстие оптической системы, определяемое размерами линз или диафрагмами. Апертура определяется апертурным углом и показателем преломления среды между объектом и фронтальной линзой объектива.
Разрешающая способность микроскопа определяется выражением:
|
dмикр |
, |
(26) |
|||
|
2Ас |
2nD sin |
||||
где λ – длина волны света, Ас – численная апертура объектива, nD – показатель преломления среды, заполняющей пространство между объектом и фронтальной линзой объектива, α – половина угла между двумя крайними лучами.
Для увеличения апертуры пространство между линзой объектива и объектом заполняется иммерсионной жидкостью (рис. 8).
20

Рис. 8. Схема действия сухой и иммерсионной систем [5]
Вкачестве иммерсионной жидкости применяется кедровое масло, показа-
тель преломления которого равен показателю преломления стекла (nD = 1,52), вода (nD = 1,33), глицерин (nD = 1,45), бромнафталин (nD = 1,66).
Так как показатели преломления иммерсионных жидкостей больше пока-
зателя преломления воздуха (nD = 1), то в таком случае в объектив будут попадать лучи, составляющие с осью оптической системы больший угол, чем в случае сухой системы.
Минимальные размеры частиц, которые можно наблюдать при белом свете для средней длины волны видимого диапазона (λ = 550 нм), составляют: для сухой системы 0,28 мкм, при водной иммерсии – 0,2 мкм и при масляной – 0,18 мкм.
Разрешающую способность микроскопа можно также значительно повысить, применяя для освещения свет с более короткой длиной волны. Для этого используются светофильтры с различным спектральным пропусканием (зеленый λ = 520 нм, синий λ = 455 нм и др.). При использовании ультрафиолетового света можно добиться разрешающей способности до 0,1 мкм.
Взависимости от оптических свойств объекта оптической микроскопии применяются различные методы освещения [6]. Основной целью данного выбора является получение наиболее контрастного изображения.
Метод светлого поля в проходящем свете позволяет получать равномерно освещенное поле в плоскости изображения. При этом свет из конденсора проходит через объект и объектив. Изображение объекта становится видимым вследствие частичного поглощения и отклонения отдельными его элементами падающего на них света.
Метод светлого поля в отраженном свете основан на освещении объекта сверху через объектив, который одновременно выполняет роль конденсора. Как разновидность данного метода можно выделить метод косого освещения. Отличие между ними состоит в том, что свет на объект направляют под большим углом. Такой способ освещения придает изображению объекта высокую контрастность, а также иногда позволяет оценить рельеф исследуемого образца.
Метод темного поля в проходящем свете дает возможность точно опреде-
21

лить контуры рассматриваемых объектов, так как на темном фоне образуются светлые изображения объекта. При использовании метода темного поля в проходящем свете свет от осветителя и зеркала направляется на объект конденсором специальной конструкции. Основная часть лучей образует пучок в виде полого конуса и не попадает в объектив. Изображение в объективе формируется при помощи небольшой части лучей, рассеянных частицами внутрь конуса и прошедших в объектив.
Метод темного поля в отраженном свете основан на освещении объекта сверху с помощью специальной кольцевой системы, называемой эпиконденсором. В таком случае изображение образуется только рассеянными лучами, имеющими слабую интенсивность. Поэтому для освещения объекта используются яркие источники света. В этом случае изображение частиц имеет вид ярко светящихся тел на совершенно темном фоне. На рис. 9 приведены изображения частиц МоО3·nH2O, полученных методом светлого (а) и темного (б) поля.
Рис. 9. Изображения частиц МоО3·nH2O, полученных методом: светлого поля в проходящем свете (а) и темного поля в отраженном свете (б).
Увеличение 900Х
Метод исследования в поляризованном свете применяют для изучения объектов, элементы которого имеют неодинаковые оптические свойства по различным направлениям. Использование поляризационного света дает возможность исследовать структуру и оптические свойства частиц.
Метод фазового контраста основан на том, что при прохождении через элементы объекта с различными показателями преломления световая волна претерпевает изменения, приобретая так называемый фазовый рельеф. Это значительно увеличивает контрастность изображения. Фазовые изменения световой волны преобразуются с помощью специального устройства в изменение амплитуды волны, что приводит к изменению интенсивности света, которая и воспринимается наблюдателем.
Флюоресцентная микроскопия позволяет в объекте сложного состава рассмотреть частицы различных веществ. Вследствие освещения объекта снизу или сверху сине-фиолетовыми или ультрафиолетовыми лучами возбуждается флюоресценция объекта. При этом вещество испускает видимый свет с харак-
22
Классический метод, который используют при оценке размеров броуновских частиц, описанный практически во всех физических практикумах, метод наложения на препарат дифракционной решетки. Несколько раз перестраивая плоскость наблюдения с препарата на решетку, оценивают размеры /диаметр/ броуновской частицы, сравнивая его с расстоянием между соседними штрихами (0,01 мм или 10 мкм).
Возможны и другие методы определения размеров частиц. Например, Перрен использовал следующий способ. Он помещал на предметном столике микроскопа капельку сильно разведенной эмульсии, не покрытой покровным стеклом. Когда испарение почти кончилось, зернышки сбегались под действием сил поверхностного натяжения и собирались местами в довольно правильные ряды. Сосчитав число зернышек, вытянутых вдоль прямой линии известной длины, или число зернышек, соприкасающихся друг с другом на известной площади, легко вычислить диаметр отдельного зернышка. Таким путем с лучшей из своих эмульсий Перрен получил для диаметра зернышка гуммигута около 0,37 мкм [12,283-284].
Компьютерная демонстрация броуновского движения
Для демонстрации броуновского движения была разработана программа, моделирующая движение одной броуновской частицы.
Данный программный продукт не требует специальной установки, достаточно скопировать с прилагаемого диска на компьютер папку «Броуновское движение», в которой находится файл Broun, и методические рекомендации.
Чтобы запустить программу нужно выбрать из папки «Броуновское движение» файл «Broun». Для выхода из программы следует щелкнуть мышью на кнопке «Выход», далее появится сообщение, нажав на кнопку которого вы подтвердите или опровергните свое решение.
При запуске exe файла открывается окно (рис.12).

Рис.12. Главное окно
Окно условно можно разделить на три области: 1) область задания параметров (рис.13),

Рис.13. Окна ввода параметров опыта
2) панель управления (рис. 14), которая состоит из следующих кнопок: «Построить/Стоп», «Очистить», «Запись в файл», «Выход» (более подробно опишем их далее),

Рис.14. Панель управления
3) область, изображающая движение броуновской частицы «Рабочая область», причем условно назовем черное поле (1), белое поле (2) (рис. 15).

Рис.15. Рабочее поле
Прежде, чем, нажать кнопку «Построить», необходимо задать параметры броуновской частицы и среды :
– температуру системы,
– вязкость среды,
– радиус броуновской частицы,
– время регистрации (т.е. интервал времени, через которое регистрируется броуновская частица),
количество перемещений, совершенных броуновской частицей, выводится на экран монитора автоматически.
После введения начальных параметров пользователь должен нажать кнопку «Построить».
В области поля (1) отображается броуновская частица (белого цвета), движущаяся в среде (черного цвета), в области поля (2) строится упрощенная траектория броуновской частицы в виде ломанной линии, вершины которой отмечаются через равные промежутки времени.
При каждом новом запуске модели частица движется по новой траектории.
Для перезапуска модели следует нажать на панели управления кнопку «Стоп», изменить параметры, если это необходимо, и кликнуть «Построить».
Кнопка «Очистить» выполняет функцию сброса параметра «количество перемещений», а так же очищает «Рабочее поле».

При нажатии на кнопку «Запись в файл» пользователь получает возможность записать параметры среднего смещения , просчитываемые программой. Полученные данные могут использоваться для дальнейших расчетов.
При нажатии на «Выход» происходит закрытие приложения.







Пользователь может воспользоваться меню, в котором имеются ссылки «Выход», «Запись в файл» (описанные выше), а так же ссылки «О программе», «С чего начать».
При нажатии ссылки «О программе» открывается окно «О программе» (рис.16), в котором вниманию пользователя предоставлена информация о разработанном программном продукте: информация о разработчиках, среде, в которой была создана компьютерная демонстрация «Броуновское движение».

Рис.16. Информационное окно «О программе»
При нажатии ссылки «С чего начать» открывается окно с одноименным названием (рис.17), в котором описаны правила работы с программой.

Рис.17. Информационное окно «С чего начать»
