Как определить диаметр окружности по координатам
Найти диаметр окружности по координатам
Как найти диаметр окружности

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
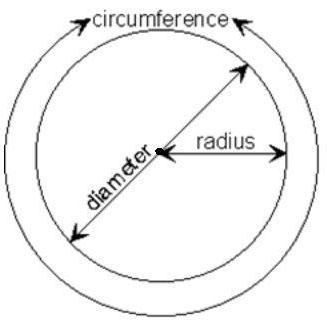
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Как посчитать диаметр окружности
Онлайн калькулятор
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Каков диаметр (d) если длина окружности C?
Формула
d = C /π , где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её радиус r?
Формула
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её площадь S?
Формула
d = √ 4S /π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см 2 , то его диаметр примерно равен 2.52 см.
Уравнение окружности.
Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.
В формулировке окружности упоминается расстояние между точкой окружности и центром.
Формула расстояния между двумя точками М1(х1; у1) и М2(х2; у2) имеет вид:
,
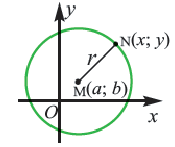
Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х0; у0) и радиусом r.
Отметим произвольную точку М(х; у) на этой окружности.
.
Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.
Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х0 ) 2 +(у – у0 ) 2 = r 2 .
Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х0; у0) и радиусом r имеет вид:
В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):
Как посчитать диаметр окружности
Онлайн калькулятор
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Каков диаметр (d) если длина окружности C?
Формула
d = C /π , где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её радиус r?
Формула
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её площадь S?
Формула
d = √ 4S /π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см 2 , то его диаметр примерно равен 2.52 см.
Как вычислить диаметр окружности: формула и пояснения
Нас окружает множество предметов. И многие из них имеют круглую форму. Она задана им для удобного использования. Взять, например, колесо. Если бы оно было изготовлено в форме квадрата, то как бы катилось по дороге?
Для того чтобы изготовить предмет круглой формы, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что же представляет собой это понятие.
Круг и окружность
Окружностью является множество точек, которые размещены на равном расстоянии от основной точки — центра. Это расстояние называется радиусом.

Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.
А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.
Что такое длина окружности?
После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.

Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.
Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.
Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.
Формула окружности через диаметр
Поскольку длина очертания пропорциональна к радиусу, то и соответственно пропорциональна диаметру. Поэтому ее длину мы условно означим буквой C, диаметр — d. Поскольку соотношение длины очертания и диаметра — постоянное число, то его можно определить.
Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π. Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.
Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π.
Если мы будем определять длину разных очертаний, то если известен их диаметр, формула будет применена одна и та же. Поскольку знак π — это приблизительное исчисление, то и было решено умножать диаметр на 3,14 (число, округленное до сотых).
Как вычислить диаметр: формула
На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания. Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π. Это будет выглядеть так d = C / π.

Рассмотрим, как эта формула действует на практике. К примеру, нам известна длина очертания колодца, следует вычислить его диаметр. Измерить его невозможно, поскольку из-за погодных условий нет доступа к нему. А задача у нас — изготовить крышку. Что будем делать в таком случае?
Нужно воспользоваться формулой. Возьмем длину очертания колодца — к примеру, 600 см. В формулу ставим конкретное число, а именно С = 600 / 3,14. В результате мы получим приблизительно 191 см. Округлим результат до 200 см. Затем с помощью циркуля рисуем круглую линию с радиусом в 100 см.
Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому. Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.
Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.
Как посчитать диаметр окружности
Онлайн калькулятор
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Каков диаметр (d) если длина окружности C?
Формула
d = C /π , где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её радиус r?
Формула
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её площадь S?
Формула
d = √ 4S /π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см 2 , то его диаметр примерно равен 2.52 см.
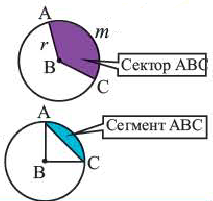
Радиус и диаметр окружности

Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).
Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.
Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности
Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.
Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.

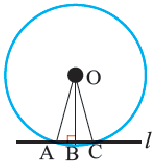
На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;
Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.
Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.
Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.
Формула радиуса окружности через диаметр:
Формула диаметра окружности через радиус:
Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.
Существует радиус вписанной окружности
и радиус описанной окружности.
Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.
Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.
Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.
[spoiler title=”источники:”]
http://poschitat.online/diametr-okruzhnosti
http://colibrus.ru/radius-i-diametr-okruzhnosti/
[/spoiler]
Содержание:
Окружность:
Определение: Кривой второго порядка называется линия, описываемая уравнением 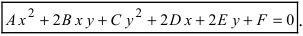
Замечание: Если коэффициенты 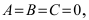
При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки 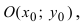 называемой центром окружности, на расстояние R, которое называется радиусом окружности.
называемой центром окружности, на расстояние R, которое называется радиусом окружности.
Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:
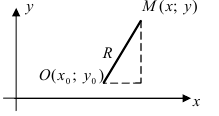
Рис. 27. Вывод уравнения окружности.
Из рисунка видно, что по теореме Пифагора 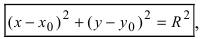 которое определяет уравнение окружности (Рис. 28):
которое определяет уравнение окружности (Рис. 28): 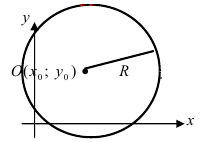
Рис. 28. Окружность. 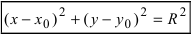
Если 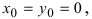 то уравнение принимает вид
то уравнение принимает вид 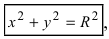 который называется каноническим уравнением окружности.
который называется каноническим уравнением окружности.
Пример:
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 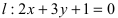 является касательной к окружности.
является касательной к окружности.
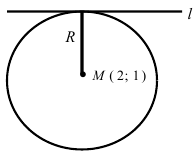
Решение:
Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.
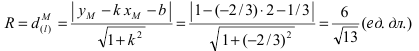
В уравнении окружности 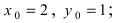 таким образом оно имеет вид:
таким образом оно имеет вид: 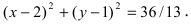
Пример:
Составить уравнение окружности, касающейся двух параллельных прямых 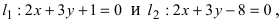 причем одной из них в т. А (1; 2).
причем одной из них в т. А (1; 2).
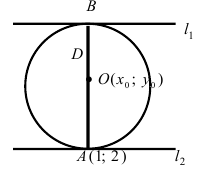
Решение:
Прежде всего определим, на какой из прямых 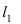 или
или 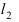 лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых
лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых 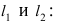
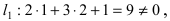 следовательно, точка A(1; 2) принадлежит линии
следовательно, точка A(1; 2) принадлежит линии 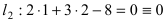 (в сокращенной форме это предложение пишут так:
(в сокращенной форме это предложение пишут так: 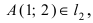 где значок
где значок 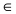 означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой
означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой 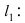
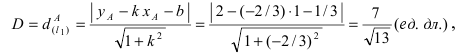
а радиус окружности 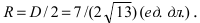 Найдём координаты центра окружности точки
Найдём координаты центра окружности точки 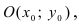 которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки
которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки 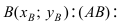 перейдем от общего уравнения прямой
перейдем от общего уравнения прямой 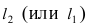 к уравнению прямой с угловым коэффициентом
к уравнению прямой с угловым коэффициентом 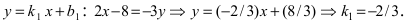 Так как прямая
Так как прямая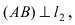 то её угловой коэффициент
то её угловой коэффициент 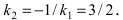 Прямая (АВ) проходит через известную точку A(1;2), следовательно,
Прямая (АВ) проходит через известную точку A(1;2), следовательно, 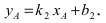 Отсюда находим
Отсюда находим 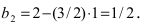 Таким образом,уравнение прямой (АВ):
Таким образом,уравнение прямой (АВ):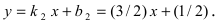
Найдем координаты точки B, которая является пересечением прямых 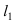 и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых
и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых 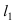 и (АВ): (В):
и (АВ): (В): 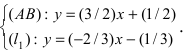 Подставим выражение для переменной у из второго у равнения в первое, получим
Подставим выражение для переменной у из второго у равнения в первое, получим 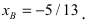 Подставив это значение во второе уравнение системы, найдем
Подставив это значение во второе уравнение системы, найдем 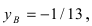 т.е.
т.е. 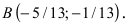
Для вычисления координат точки О применим формулы деления отрезка пополам (О): 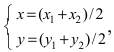 в этой формуле
в этой формуле 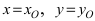 (координаты точки О),
(координаты точки О), 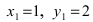 (координаты точки А),
(координаты точки А), 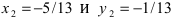 (координаты точки В), следовательно,
(координаты точки В), следовательно, 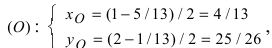 т.е. координаты точки О
т.е. координаты точки О 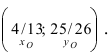
Таким образом, уравнение искомой окружности имеет вид: 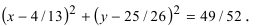
Окружность в высшей математике
Рассмотрим уравнение

которое получается из уравнения (I), если положить 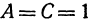 ,
, 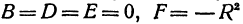 .
.
Если в формулу, выражающую расстояние между двумя точками, подставить 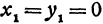 ,
, 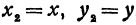 , то получим
, то получим 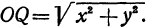 Из уравнения (1) находим, что
Из уравнения (1) находим, что 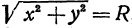 , т. е.
, т. е. 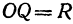 . Это значит, что все точки
. Это значит, что все точки 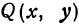 , координаты которых удовлетворяют уравнению (1), находятся на расстоянии
, координаты которых удовлетворяют уравнению (1), находятся на расстоянии 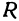 от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса
от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса  с центром в начале координат. Аналогично получаем, что уравнение
с центром в начале координат. Аналогично получаем, что уравнение 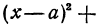
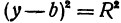 определяет окружность радиуса
определяет окружность радиуса  с центром в точке
с центром в точке 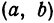 .
.
Пример:
Найдем уравнение окружности с центром в точке  и радиусом, равным 10.
и радиусом, равным 10.
Решение:
Полагая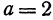 ,
, 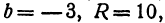 получим
получим 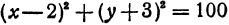 .
.
Разрешим это уравнение относительно 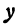 , будем иметь
, будем иметь
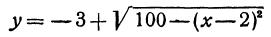
и
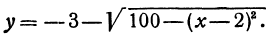
Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.
Центральный угол. Градусная мера дуги
Дуга окружности. Если отметить на окружности точки  и
и  , то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка
, то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка 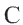 является какой-либо точкой дуги
является какой-либо точкой дуги 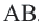 , то
, то 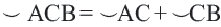 . Если точки
. Если точки  и
и  являются концами диаметра, го каждая дуга является полуокружностью.
являются концами диаметра, го каждая дуга является полуокружностью.
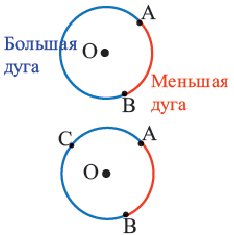
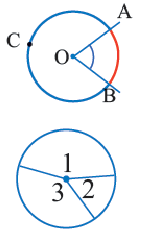
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла: 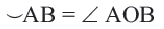
Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна 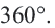
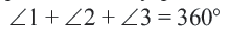
Дуги окружности и их величины

Пример: 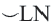 минорная дуга:
минорная дуга: 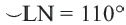
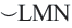 мажорная дуга:
мажорная дуга: 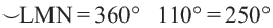
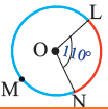
Конгруэнтные дуги
В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.
Если 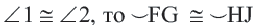
Если 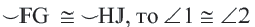
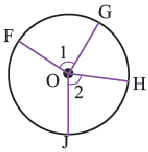
Длина дуги
Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.
Длина дуги в 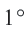 равна
равна 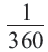 части длины окружности.
части длины окружности.
Длина дуги, соответствующей центральному углу с градусной мерой 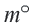 , составляет
, составляет 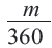 части длины окружности:
части длины окружности: 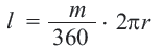
Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)
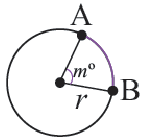
Пример №1
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу 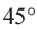 .
.
Решение:
Так как центральный угол 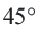 составляет
составляет 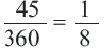 часть полного угла, то длина искомой дуги:
часть полного угла, то длина искомой дуги: 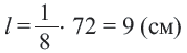
Пример №2
Найдите длину дуги, соответствующей центральному углу 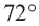 в окружности радиусом 15 см.
в окружности радиусом 15 см.
Решение: подставляя значения 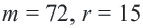 в формулу длины дуги находим:
в формулу длины дуги находим: 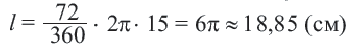
Окружность и хорда
Теорема о конгруэнтных хордах
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.
Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.
1)Если 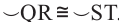 , то
, то 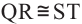
2)Если 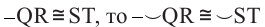
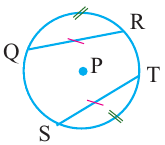
Доказательство теоремы 1:
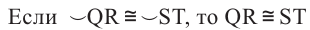

Теорема о серединном перпендикуляре хорд
Теорема 2.
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.
Если 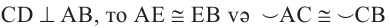
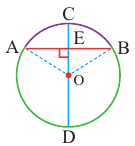
Доказательство теоремы 2.
Дано:  – центральный угол,
– центральный угол, 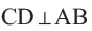
Докажите: 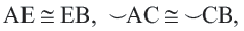
Начертите радиусы 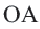 и
и 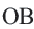 окружности.
окружности.
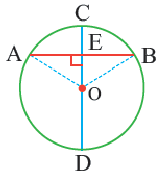
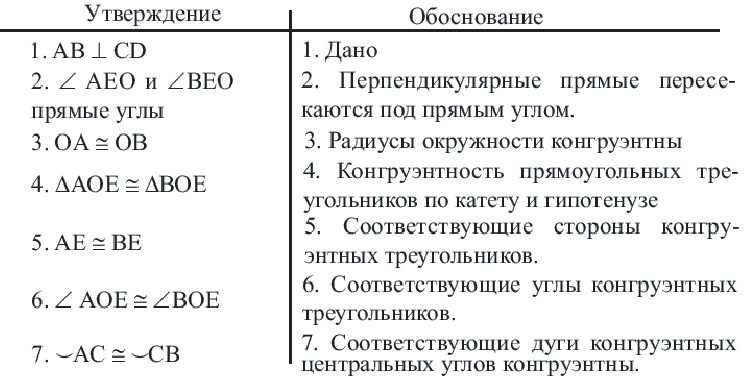
Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.
Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если 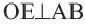 , то
, то 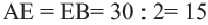 . Из
. Из 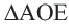 по теореме Пифагора имеем:
по теореме Пифагора имеем: 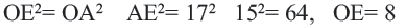
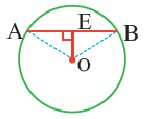
Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности
Теорема 3.
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.
Если 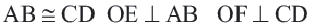 , то
, то 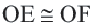
Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.
Доказательство теоремы 3
Дано: Окружность с центром 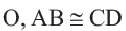
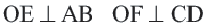
Докажите: 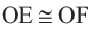
Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам.  и
и  – серединные перпендикуляры конгруэнтных хорд
– серединные перпендикуляры конгруэнтных хорд 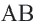 и
и 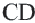 .
.  , так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности
, так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности 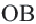 и
и 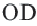 :
: 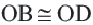 . Прямоугольные треугольники,
. Прямоугольные треугольники, 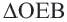 и
и 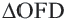 конгруэнтны (по катету и гипотенузе). Так как
конгруэнтны (по катету и гипотенузе). Так как  и
и  являются соответствующими сторонами данных треугольников, то они конгруэнтны:
являются соответствующими сторонами данных треугольников, то они конгруэнтны: 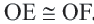 . Теорема доказана.
. Теорема доказана.
Задача. Хорды  и
и  находятся на одинаковом расстоянии от центра окружности.
находятся на одинаковом расстоянии от центра окружности. 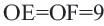 . Если радиус окружности равен 41 единице, то найдите
. Если радиус окружности равен 41 единице, то найдите 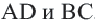 .
.
Решение: Так как хорды  и
и  находятся на одинаковом расстоянии от центра, то они конгруэнтны:
находятся на одинаковом расстоянии от центра, то они конгруэнтны: 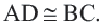
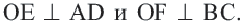 Соединим точки
Соединим точки 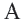 и
и 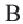 с точкой
с точкой 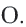 В прямоугольном треугольнике
В прямоугольном треугольнике 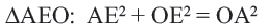
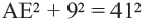 ;
; 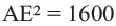 ;
; 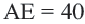 ;
; 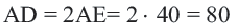
Так как 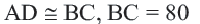
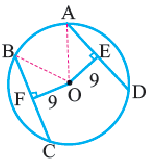
Угол, вписанный в окружность
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.
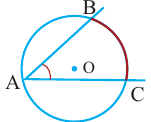
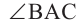 является углом вписанным в окружность с центром
является углом вписанным в окружность с центром  , а
, а  дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
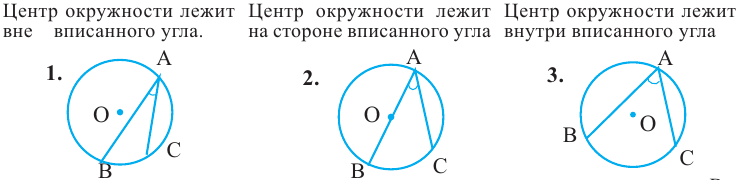
Угол, вписанный в окружность:
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается. 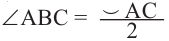
Доказательство (текстовое): 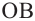 и
и 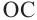 радиусы окружности и
радиусы окружности и 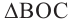 равнобедренный треугольник. Значит,
равнобедренный треугольник. Значит, 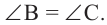 Так как
Так как 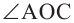 является внешним углом
является внешним углом 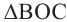 ,
, 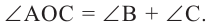 Если примем, что
Если примем, что 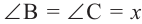 , то
, то 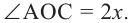 Так как градусные меры центрального угла и опирающейся на него дуги равны, то
Так как градусные меры центрального угла и опирающейся на него дуги равны, то 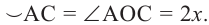 Следовательно,
Следовательно, 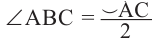 .
.
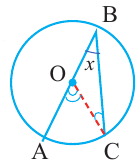
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.
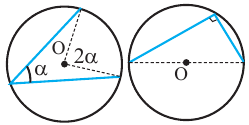
Конгруэнтные углы, вписанные в окружность
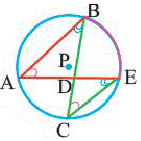
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. 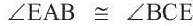 ,
, 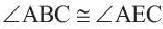 .
.
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если 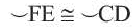 , то
, то 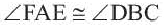 .
.

Касательная к окружности
Касательная. Признак касательной
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
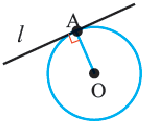
Прямая 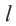 является касательной к окружности. Значит,
является касательной к окружности. Значит, 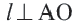 Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
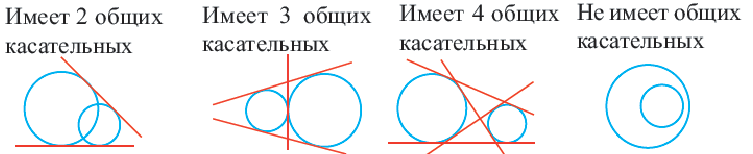
Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.

Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.
Доказательство теоремы 1. Если прямая  – касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая
– касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая  не перпендикулярна радиусу
не перпендикулярна радиусу 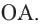 Проведем
Проведем 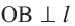 и на прямой
и на прямой  выделим отрезок
выделим отрезок 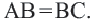 Тогда
Тогда 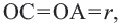 так как
так как 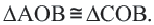 Значит, точка
Значит, точка 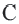 также находится на окружности. То есть прямая
также находится на окружности. То есть прямая  имеет с окружностью две общие точки, что противоречит условию. Значит,
имеет с окружностью две общие точки, что противоречит условию. Значит, 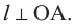
Свойства касательных, проведенных к окружности из одной точки
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.
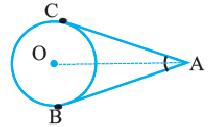
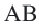 и
и 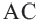 касательные, проведенные из точки
касательные, проведенные из точки 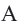 к окружности с центром
к окружности с центром 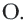
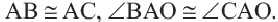
Углы, образованные секущими и касательными
Прямая, имеющая две общие точки с окружностью, называется секущей окружности.
Углы между двумя секущими
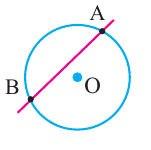
Вершина угла находится внутри окружности
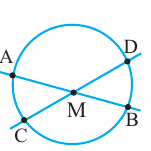
Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному. 
Углы между касательной и секущей
Вершина угла находится на окружности
Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.
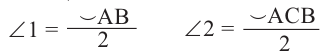
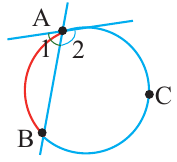
Углы, образованные касательной и секущей
Вершина угла находится вне окружности
Теорема 1.
Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.
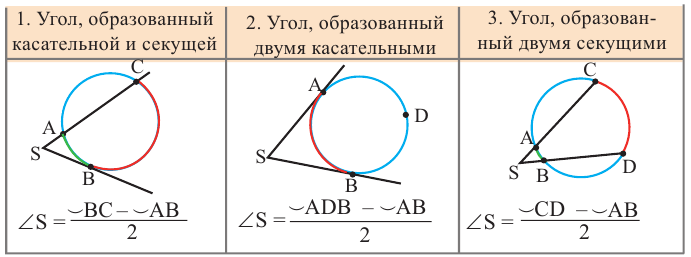
Отрезки секущих и касательных
Длина отрезков, секущих окружность
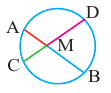
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.
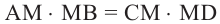
Теорема 2. Если из точки  провести две прямые, пересекающие окружность соответственно в точках
провести две прямые, пересекающие окружность соответственно в точках  и
и 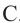 ,
, 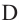 и
и 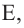 то верно равенство
то верно равенство 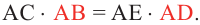
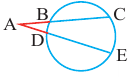
Теорема 3. Если из точки 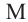 проведены прямая, которая пересекает окружность в точках
проведены прямая, которая пересекает окружность в точках  и
и  и касательная к окружности в точке
и касательная к окружности в точке 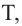 то верно равенство:
то верно равенство: 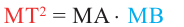
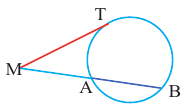
Уравнение окружности
Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом  и с центром в начале координат. Расстояние между центром окружности
и с центром в начале координат. Расстояние между центром окружности 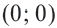 и ее любой точкой
и ее любой точкой 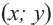 равно радиусу
равно радиусу  окружности.
окружности.
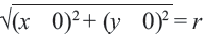 Расстояние между двумя точками
Расстояние между двумя точками
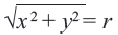 Упрощение
Упрощение
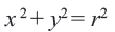 Возведение обеих частей в квадрат
Возведение обеих частей в квадрат
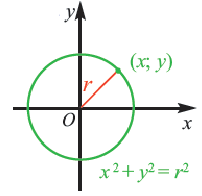
Уравнение окружности с центром в начале координат и радиусом 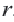 :
: 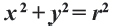
Например, уравнение окружности с центром в начале координат 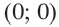 и радиусом 2 имеет вид:
и радиусом 2 имеет вид: 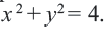
По формуле расстояния между центром окружности 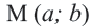 и точки
и точки 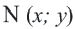 на окружности радиуса
на окружности радиуса 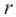 имеем
имеем 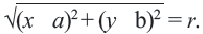 Возведя в квадрат обе части, получаем уравнение окружности с центром в точке
Возведя в квадрат обе части, получаем уравнение окружности с центром в точке 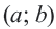 и радиусом
и радиусом 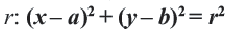
Например, уравнение окружности с центром в точке 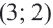 и радиусом 4 имеет вид:
и радиусом 4 имеет вид: 
Пример №3
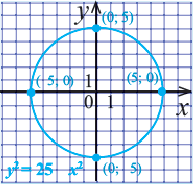
Постройте на координатной плоскости окружность, заданную уравнением 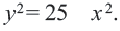
Решение: Напишем уравнение в виде 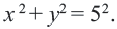 Как видно,
Как видно, 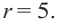
Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 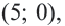
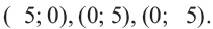 Проведем окружность через эти точки.
Проведем окружность через эти точки.
Пример №4
Точка 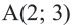 находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
Решение: Записав координаты точки 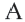 в уравнении
в уравнении 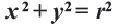 , получим:
, получим: 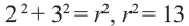 Уравнение этой окружности:
Уравнение этой окружности: 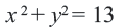
Пример №5
Найдем центр и радиус окружности, заданной уравнением 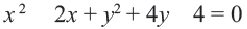
Решение: 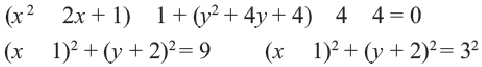
Центр окружности точка 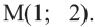 Радиус
Радиус 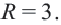
Пример №6
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 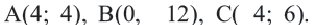 На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 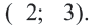 Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности,
Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности, 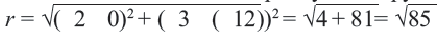
Уравнение окружности: 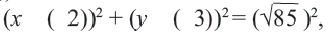
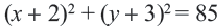
Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.
Координаты точек, находящихся на окружности, и тригонометрические отношения
Если точка 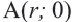 при повороте радиуса
при повороте радиуса 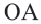 вокруг точки
вокруг точки 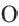 против движения часовой стрелки на угол
против движения часовой стрелки на угол 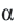 преобразуется в точку
преобразуется в точку 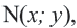 то
то 
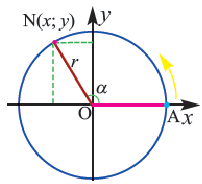
Для координат точки 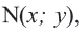 соответствующей углу поворота
соответствующей углу поворота  на окружности, верны формулы
на окружности, верны формулы 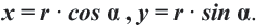 В этих формулах
В этих формулах  – угол, отсчитываемый от положительной оси
– угол, отсчитываемый от положительной оси 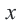 против движения часовой стрелки. Если точка
против движения часовой стрелки. Если точка 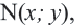 не находится на оси ординат, то
не находится на оси ординат, то 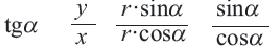 .
.
Синусы смежных углов равны, а косинусы взаимно противоположны.

Из этих формул при 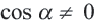 почленным делением получаем:
почленным делением получаем:
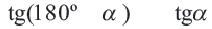
С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.
Сектор и сегмент
Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.
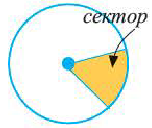
Например, часть круга, соответствующая центральному углу 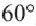 , составляет
, составляет 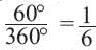 часть всего круга. Так как площадь круга
часть всего круга. Так как площадь круга 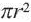 , то площадь этого сектора будет
, то площадь этого сектора будет  Сегмент часть круга, ограниченная хордой и соответствующей дугой.
Сегмент часть круга, ограниченная хордой и соответствующей дугой.
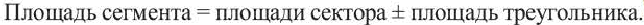
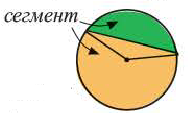
Площадь сектора
Площадь сектора: 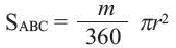
Площадь сегмента: 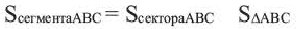
Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь 
- Эллипс
- Гипербола
- Парабола
- Многогранник
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
Найди верный ответ на вопрос ✅ «Точки А ( – 4; 7) В (2; – 1) являются концами диаметра окружности. Найти диаметр окружности и координаты её центра. Запишите уравнение …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Геометрия » Точки А ( – 4; 7) В (2; – 1) являются концами диаметра окружности. Найти диаметр окружности и координаты её центра. Запишите уравнение окружности.
Задача №1. Определить центр и радиус окружности, заданной уравнением х²+у²-2х+4y-20=0.
Решение. Так как в заданном уравнении коэффициенты при х² и у² равны между собой и отсутствует член с произведением координат, го заданное уравнение действительно представляет собой уравнение окружности. Чтобы определить координаты центра и радиус окружности, необходимо уравнение привести к каноническому виду:
(х²-2х)+(y²+4у)=20, (x²-2х+1)+(у²+4х+4)=25, (x-1)²+(y+2)²=25.
Координаты центра и радиус окружности можно найти, не приводя данное уравнение к каноническому виду,
Рис.1
достаточно сравнить данное уравнение с уравнением окружности в общем виде:

Ответ: (1, —2), R = 5.
Задача №2. Составить уравнение окружности, проходя¬щей через точки А (—1;1) и В (1;-3), если центр ее лежит на прямой 2х-у+1=0.
Решение. Каноническое уравнение окружности:
(x-a)²+(y-b)² = r².
Так как окружность проходит через точки А и B, то координаты этих точек должны удовлетворять уравнению окружности. Имеем два уравнения:
(-1-а)² + (1-b)²=r², (1-а)² + (-3-b)² = r².
Если центр окружности лежит на прямой 2х-у+1=0, то координаты центра также должны удовлетворить уравнению прямой.
Имеем третье уравнение: 2а-b+1=0.

Рис.2
Решим систему уравнений:
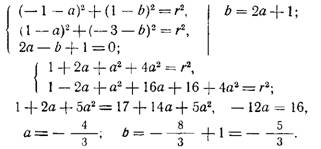
Таким образом, координаты центра окружности найдены:
![]()
Чтобы определить г², получим: г² = 1+2а+5а²,
![]()
Уравнение окружности:
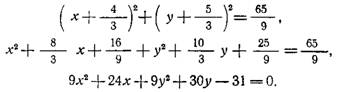
Ответ: 9х² + 9y² + 24x + 30у – 31 =0.
Задача №3. Составить уравнение окружности, если ее центр находится в точке С(5;4) и окружность отсекает от прямой х+2у-3=0 хорду, длина которой равна 8.
Решение. Искомое уравнение будет иметь вид:
(x-5)²+(у-4)²=r².
Определим расстояние центра С от данной прямой:
![]()
Так как радиус, перпендикулярный к хорде, делит ее пополам, то половина хорды будет равна 4 единицам.
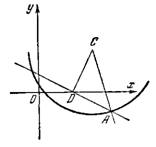
Рис.3
По теореме Пифагора имеем:
г²=4²+CD²=16+20=36, r² = 36, r = 6.
Уравнение окружности: (х -5)²+(у – 4)² = 36.
Ответ: (х -5)²+(у – 4)² = 36.
Задача №4. Составить уравнение окружности, касающейся двух параллельных прямых 2х+у-5=0 и 2х+y+15=0, причем одной из них — в точке А(2; 1).
Решение. Определим диаметр окружности, для чего используем формулу расстояния точки от прямой
![]()
Уравнение прямой 2x+y+15=0, точка А(2; 1)
![]()
Воспользовавшись координатами точки A, можем составить такое уравнение:
(2 – а)²+(1 – b)² = 20.
Второе уравнение с неизвестными а и b получим, определив расстояние точки С от первой прямой
![]()
Поскольку точка С лежит по одну сторону от прямой
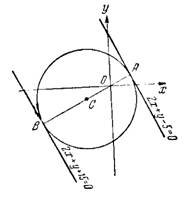
Рис. 4
вместе с началом координат, то расстояние АС<0.
Имеем систему уравнений:
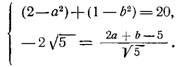
Решая полученную систему уравнений, найдем а=-2; b=-1.
Эту задачу рекомендуем решить самостоятельно другим способом.
Указания. Составить уравнение перпендикуляра А В к данным прямым и найти координаты точки В.
Ответ: (x+2)²+(у + 1)²=20.
-
Геометрия
Предыдущий вопрос
Следующий вопрос
иван1229
8 лет назад
Ответ
Ответ дан
kytanidze
вектор АВ(4+4;7-1)=(8;6) |AB|=√64+36=10 D=10 R=5
b)центр окружности это середина отрезкаАВ обозначим ее М(х;у) х=-4+4/2=0
у=1+7/2=4 М(0;4)
уравнение окружности (х-0)²+(у-4)²=R²или х²-(у-4)²=25
Ответы и объяснения
- иван1229
Не тот ответ, который тебе нужен?
Найди нужный
