Как найти диаметр окружности описанной около шестиугольника - Сайт, где вы сможете решить свои вопросы

Как найти диаметр окружности описанной около правильного шестиугольника

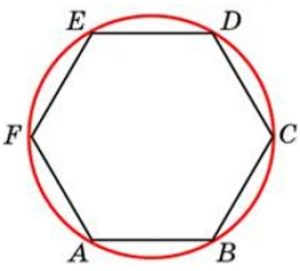
Правильный шестиугольник

1. Все углы правильного шестиугольника равны 120°

2. Все стороны правильного шестиугольника равны между собой

3. Периметр правильного шестиугольника

4. Формула площади правильного шестиугольника

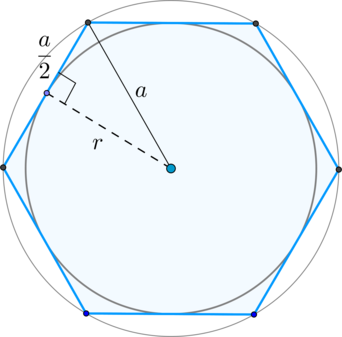
5. Радиус описанной окружности правильного шестиугольника

6. Диаметр описанной окружности правильного шестиугольника

7. Радиус вписанной окружности правильного шестиугольника

8. Соотношения между радиусами вписанной и описанной окружностей

9. Угол , угол , угол , откуда следует, что треугольник – прямоугольный с гипотенузой равной . Следовательно,

10. Длина дуги AB равна

11. Формула площади сектора

Решение №2077 Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.

Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.

Найдем сторону шестиугольника:

108:6 = 18

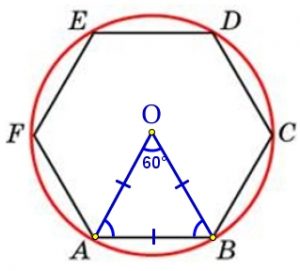
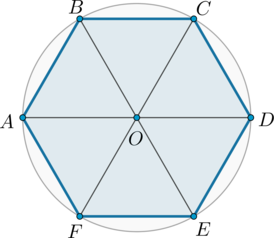
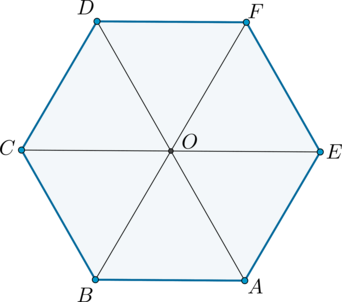
Рассмотрим треугольник AOB. Он равносторонний, т.к. ∠АОВ = 360°/6 = 60°, АО = ОВ. Тогда радиус равен стороне шестиугольника:

АВ = ОВ = r = 18

Найдём диаметр:

d = 2·r = 2·18 = 36

Ответ: 36.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5. Количество оценок: 0

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Правильный шестиугольник и его свойства

Определение

Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.

Замечание

Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]

Пример

Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac <4-2>4cdot 180^circ=90^circ) ;

каждый угол правильного шестиугольника равен (dfrac<6-2>6cdot 180^circ=120^circ) .

Теоремы

1. Около любого правильного многоугольника можно описать окружность, и притом только одну.

2. В любой правильный многоугольник можно вписать окружность, и притом только одну.

Следствия

1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.

2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.

Теорема

Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfrac<180^circ>n\ r&=Rcdot cosdfrac<180^circ>n end]

Свойства правильного шестиугольника

1. Сторона равна радиусу описанной окружности: (a=R) .

2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.

3. Все углы правильного шестиугольника равны (120^circ) .

4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt<3>><2>a^2) .

5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.

6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).

Замечание

В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac<360^circ>) .

[spoiler title=”источники:”]

Решение №2077 Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.

http://shkolkovo.net/theory/77

[/spoiler]

Источник

Задания

Версия для печати и копирования в MS Word

Тип 1 № 54065

Периметр правильного шестиугольника равен 174. Найдите диаметр описанной окружности.

Решение.

Это задание ещё не решено, приводим решение прототипа.

Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.

Найдем сторону шестиугольника: 72 : 6 = 12.

Рассмотрим треугольник AOB. Радиус описанной вокруг шестиугольника окружности равен его стороне, а диаметр вдвое больше. Поэтому он равен 24.

Ответ: 24.

Аналоги к заданию № 27929: 54059 54103 54107 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.7 Вписанная окружность и описанная окружность правильного многоугольника

Прототип задания

Видеокурс

Источник

Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.

Источник: mathege

Решение:

Найдем сторону шестиугольника:

108:6 = 18

Рассмотрим треугольник AOB. Он равносторонний, т.к. ∠АОВ = 360°/6 = 60°, АО = ОВ. Тогда радиус равен стороне шестиугольника:

АВ = ОВ = r = 18

Найдём диаметр:

d = 2·r = 2·18 = 36

Ответ: 36.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 2

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Запись опубликована:16.09.2021
Рубрика записи1. Прототипы темы: «Планиметрия»
Автор записи:Andrei Maniakin

Источник

6. Геометрия на плоскости (планиметрия). Часть II

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Правильный шестиугольник

Правильный шестиугольник – выпуклый шестиугольник, у которого все углы равны и все стороны равны.

(blacktriangleright) Каждый угол правильного шестиугольника равен (120^circ).

(blacktriangleright) Около правильного шестиугольника можно описать окружность: ее радиус равен его стороне.

(blacktriangleright) Большие диагонали правильного шестиугольника делят его на (6) равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.

(blacktriangleright) Центры вписанной и описанной около правильного шестиугольника окружностей есть точка пересечения больших диагоналей этого шестиугольника.

(blacktriangleright) Площадь правильного шестиугольника со стороной (a) равна [S=dfrac{3sqrt3}2a^2]

Задание
1

#2430

Уровень задания: Равен ЕГЭ

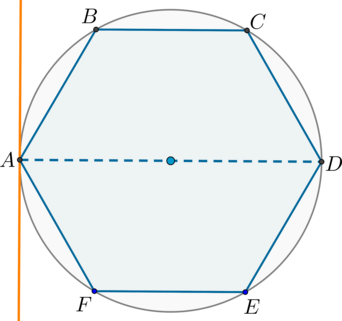
К окружности, описанной около правильного шестиугольника (ABCDEF), в точке (A) проведена касательная. Найдите угол между этой касательной и прямой (AD). Ответ дайте в градусах.

Т.к. центр описанной около правильного шестиугольника окружности есть точка пересечения больших диагоналей, то он лежит на отрезке (AD), то есть (AD) – диаметр описанной окружности. Т.к. радиус, проведенный в точку касания, перпендикулярен касательной, то угол между касательной и (AD) равен (90^circ).

Ответ: 90

Задание
2

#2427

Уровень задания: Равен ЕГЭ

Радиус вписанной в правильный шестиугольник окружности равен (sqrt{12}). Найдите радиус описанной около этого шестиугольника окружности.

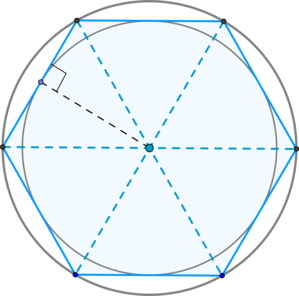
По свойству правильного шестиугольника радиус (r) вписанной окружности равен перпендикуляру, проведенному из центра правильного шестиугольника (центр вписанной и описанной окружности) к стороне шестиугольника; причем этот перпендикуляр падает в середину стороны.

Также по свойству правильного шестиугольника радиус описанной окружности равен его стороне (a). Тогда из прямоугольного треугольника:

[a^2=left(frac a2right)^2+r^2 quad Rightarrow quad a=dfrac 2{sqrt3},r quadRightarrow
quad a=dfrac2{sqrt3}cdot sqrt{12}=4]

Таким образом, и радиус описанной окружности равен (4).

Ответ: 4

Задание
3

#3589

Уровень задания: Равен ЕГЭ

Периметр правильного шестиугольника равен (72). Найдите диаметр описанной окружности.

Если провести все большие диагонали правильного шестиугольника, то они пересекутся в одной точке, которая и будет центром описанной около него окружности (свойство правильного шестиугольника). Рассмотрим чертеж:

Так как угол правильного шестиугольника равен (180^circ(6-2):6=120^circ), а большие диагонали являются биссектрисами углов, то, например, (angle BAO=angle ABO=60^circ), следовательно, (triangle ABO) – равносторонний. То есть радиус окружности равен (AO) и равен (AB). Так как периметр шестиугольника равен (72), то его сторона равна (72:6=12). Тогда диаметр описанной окружности равен (2cdot 12=24).

Ответ: 24

Задание
4

#3588

Уровень задания: Равен ЕГЭ

Найдите радиус окружности, вписанной в правильный шестиугольник со стороной (sqrt3).

Для любого многоугольника, в который можно вписать окружность, верно (S=pcdot r), где (p) – полупериметр, а (r) – радиус вписанной окружности.
Площадь правильного шестиугольника со стороной (a) равна (S=dfrac{3sqrt3}2a^2), полупериметр равен (3a), тогда [dfrac{3sqrt3}2cdot (sqrt3)^2=3sqrt3cdot rquadRightarrowquad
r=1,5]

Ответ: 1,5

Задание
5

#3587

Уровень задания: Равен ЕГЭ

Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен (sqrt3).

Ответ: 2

Задание
6

#2429

Уровень задания: Равен ЕГЭ

Площадь правильного шестиугольника равна (24sqrt3). Найдите длину его большей диагонали.

По свойству правильного шестиугольника большая его диагональ в два раза больше его стороны. Следовательно, если (AB=a), то (AD=BF=CE=2a).

Т.к. эти диагонали делят правильный шестиугольник на 6 равносторонних треугольников, причем площадь каждого равна (frac{sqrt3}4 a^2), то площадь всего шестиугольника равна

[S=6cdot dfrac{sqrt3}4a^2=24sqrt3 quad Rightarrow quad a=4 quad Rightarrow
quad AD=2a=8.]

Ответ: 8

Задание
7

#666

Уровень задания: Равен ЕГЭ

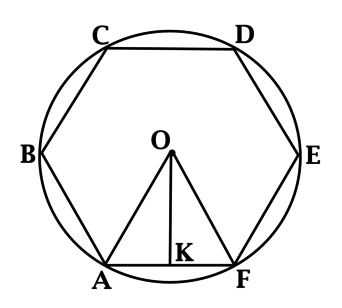
Около правильного шестиугольника (ABCDEF) описана окружность с центром в точке (O). Расстояние от точки (O) до одной из его сторон равно (4sqrt{3}). Найдите радиус этой окружности.

Радиус описанной около правильного шестиугольника окружности равен стороне этого шестиугольника.

(OK) – высота в треугольнике (AOF), опущенная из (O). Так как расстояние от точки до прямой – это длина перпендикуляра, опущенного из этой точки на эту прямую, то (OK = 4sqrt{3}).
Пусть (R) – радиус описанной окружности, тогда (OF = R), (KF = 0,5R) (так как (OK) ещё и медиана), таким образом, по теореме Пифагора (R^2 = (0,5R)^2 + (4sqrt{3})^2), откуда (R = 8).

Ответ: 8

Теме «Правильный шестиугольник и его свойства» в ЕГЭ по математике традиционно отводится сразу несколько заданий. Причем в зависимости от условия от учащегося может требоваться как развернутый, так и краткий ответ. Именно поэтому в процессе подготовки к сдаче аттестационного испытания выпускникам непременно стоит научиться решать задачи на применение свойств этой фигуры, в которых необходимо найти ее стороны, диагонали, радиус окружности со вписанным правильным шестиугольником и т. д.

Восполнить пробелы в знаниях, «прокачать» навыки и улучшить собственные знания по данной теме вам поможет образовательный проект «Школково». Наши специалисты подготовили и изложили весь базовый материал для подготовки к ЕГЭ в максимально доступной форме.

Чтобы школьники могли успешно справляться с задачами по данной теме, мы рекомендуем повторить базовые понятия: каковы свойства правильного шестиугольника, описанного около окружности, как вычисляется его площадь, чему равны его углы и т. д. Весь необходимый материал вы найдете в разделе «Теоретическая справка». Он был разработан нашими сотрудники на основе богатого практического опыта.

Для закрепления полученных знаний предлагаем потренироваться в решении соответствующих задач, а также заданий по теме «Параллелограмм в ЕГЭ». Найти их вы сможете в разделе «Каталог». Для каждого упражнения на сайте представлены алгоритм решения и правильный ответ.

Готовиться к ЕГЭ школьники из Москвы и других городов могут в режиме онлайн. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». В дальнейшем к этому заданию можно будет вернуться и, к примеру, обсудить алгоритм его решения с преподавателем.

УСТАЛ? Просто отдохни

Источник

Шестиугольник является правильным многоугольником, так как у него все стороны и углы равны. А значит, около любого шестиугольника можно описать окружность.

Точка O –центр правильного многоугольника, также является центром описанной вокруг него окружности.
Центр правильного многоугольника равноудален от его вершин. Отрезок, соединяющий центр с вершинами называется радиусом правильного многоугольника и также является радиусом описанной около него окружности.

Формула радиуса описанной окружности около шестиугольника
Существует классическая формула для нахождения радиуса описанной окружности около правильного многоугольника

$r={ a / { 2 sin{{180^0}/n}} }$

Для правильного шестиугольника n=6, тогда угол будет равен ${{180^0}/6}=30^0$
По тригонометрической таблице sin(30°)= 1/2
Тогда формула радиуса описанной окружности около шестиугольника имеет следующий вид
Радиус описанной окружности около шестиугольника равен его стороне

R=a=d/2

Пример расчета радиуса окружности описанной около шестиугольника
Найдите радиус окружности описанной около правильного шестиугольника, если радиус вписанной окружности в него равен sqrt{3}

Радиус описанной окружности около шестиугольника имеет вид R = a
Применив формулу радиуса вписанной окружности в шестиугольник, получаем:
Выразим сторону шестиугольника:
Выразим радиус описанной окружности через радиус вписанной: