Знак диаметра
В тех случаях, когда требуется указать размер диаметра, используют знак в виде окружности с линией « Ø ». Этот символ наносят перед размерным числом.
Примеры использования знака диаметра:
Знаки диаметра на деталях вращения цилиндрической и конической формы
Размеры наносимые при недостатке места
на размерной линии
Обозначение размеров при недостатке места
для стрелок
Диаметр – это длинна отрезка прямой соединяющей поверхности окружности. Отрезок диаметра, в любом случае проходит только через центр окружности. Обозначают его обычно латинской буквой « D » или знаком « Ø ». Если радиус окружности умножить на два, суммой будет диаметр. Все объемные тела, имеющие сферическую форму, а также те, хотя бы одно из возможных сечений которых представляет собой круг, обозначаются символами диаметра. Слово «диаметр» произошло от греческого слова «diametros» – поперечник.
Пример обозначения четырёх отверстий
с указанием диаметра
На технических чертежах диаметры обозначаются символом в виде перечеркнутой окружности « Ø ». Данный знак, ставится перед размерными числами деталей, которые могут быть как цилиндрическими, так и коническими.
В сечение конус представляет собой прямоугольный треугольник, один из катетов которого параллелен или сосен телу вращения. Его параметры имеют следующими обозначениями: « D » – больший диаметр, « d » – меньший диаметр, « L » – длина. На чертеже диаметры конуса обозначаются цифрами, перед которыми ставятся знаки « Ø » а числовое значение длинны без буквенных обозначений.
К наиболее распространенным деталям с цилиндрическими поверхностями, относятся валы различного назначения. Цилиндрические тела, образованные вращением прямоугольника около одной из его сторон обозначаются диаметром. Гладкие валы имеют некоторые конструктивные особенности, и разделяются на разновидности: прямые, ступенчатые односторонние, ступенчатые двусторонние и тяжелые. К примеру, валы асинхронных двигателей, в которых ротор сопрягается с валом методом запрессовки на наибольший его диаметр, а по обеим сторонам имеются ступени под подшипники, вентиляторы, и шкивы. Двусторонние ступенчатые валы можно встретить так же в различных механизмах там, где требуются, какие либо другие конструктивные особенности. Цилиндрические детали, как правило, имеют общую максимальную длину и наружный диаметр. В зависимости от конкретной конфигурации того или иного изделия в её состав могут входить такие элементы как внутренние и наружные канавки, ступени, выточки и др. с различными диаметрами перед значениями которых ставятся знаки « Ø ».
Пример нанесения знака диаметра
на сферической поверхности
К деталям с коническими поверхностями относятся инструментальные переходные втулки, у которых наружная и внутренняя поверхность конические. Такие втулки обеспечивают высокую точность центрирования и быстродействие смены инструмента с достаточной жёсткостью при использовании их на станках. Переходные втулки бывают короткие и длинные.
Конические инструментальные детали данного типа называются «конус Морзе» и делятся на номера. Углы, длины и диаметры переходных втулок можно взять из специальных таблиц. В табличных данных используются буквенные обозначения такие как – « d » меньший диаметр, « D » большой диаметр, « L » длина детали. На чертежах диаметры и длины обозначаются цифровыми значениями, причём перед числами диаметра ставится знак « Ø ».
«Конус Морзе» – помимо переходных втулок применяется при изготовлении хвостовиков спиральных свёрл, концевых фрез, приспособлений и оправок. Инструментальные конусы фиксируются за счёт упругой и пластической деформации. Для реализации таких соединений в шпинделях фрезерных и токарных станков, предусмотрены конические отверстия для установки вспомогательного инструмента. Кроме того у токарного станка пиноль задней бабки имеет такое же коническое отверстие.
В технике используются большое количество деталей и их элементов для обозначения, которых используется знак диаметра. Для стандартных размеров диаметров используются параметрический ряд, в который входят стандартные размеры. При разработке технических изделий расчётные диаметры округляются до ближайших их величин. При обозначении на технических чертежах знак диаметра должен сопровождаться обозначением оси штрихпунктирной линией, что указывает на круглое сечение участка детали.
13. Основные правила нанесения размеров на чертеже
По изображениям предмета на чертеже судят о его величине и величине его отдельных частей. Основанием для этого служат размерные числа, независимо от того, в каком масштабе и с какой точностью
выполнены изображения. Правила нанесения размеров на чертежах установлены ГОСТ 2.307—68.
Размеры на чертеже указывают размерными числами, размерными и выносными линиями. Размерные числа на чертежах, как правило, указывают в миллиметрах без указания единиц измерения. В тех случаях, когда необходимо применять другие единицы измерения длины, их показывают после размерного числа.
Размерные числа наносят над размерной линией, возможно ближе к ее середине. Зазор между размерным числом и размерной линией должен быть около 1,0 мм. Высоту цифр размерных чисел принимают не менее 3,5 мм (рис. 7).
Размерная линия проводится параллельно отрезку, размер которого над ней наносится. Ее проводят между выносными линиями, проведенными перпендикулярно размерным. Допускается размерные линии проводить непосредственно к линиям видимого контура, осевым и центровым. В отдельных случаях размерная линия может проводиться не перпендикулярно выносной (рис. 8). Размерные линии ограничивают стрелки (рис. 9). В отдельных случаях их проводят не полностью, а с обрывом стрелки с одной стороны (рис. 10). Размер стрелки выбирают от принятой на чертеже толщины сплошной толстой основной линии. В пределах одного чертежа величина стрелок должна быть по возможности одинаковой. Не рекомендуется в качестве размерных линий использовать контурные, осевые, центровые и выносные линии.
Если длина размерной линии мала для размещения стрелок, то размерную линию продолжают за выносные линии, и размеры наносят, как показано на рис. 11.
Выносные линии проводят от границ измерений, они являются вспомогательными и служат для размещения между ними размерных линий. Выносные линии следует по возможности располагать вне контура изображения, перпендикулярно прямолинейному отрезку, размер которого необходимо указать. Выносные линии должны выходить за концы стрелок размерных линий на 1. 5 мм (рис. 12).
Минимальное расстояние от размерной линии до параллельной ей линии должно быть 10 мм, а между параллельными размерными линиями — 7 мм.
Угловые размеры на чертежах проставляются в градусах, минутах и секундах с указанием единиц измерения. Размер угла наносят над размерной линией, которая проводится в виде дуги с центром в его вершине. Выносные линии в этом случае проводятся радиально (рис. 13).
При различных наклонах размерных линий размерные числа линейных размеров располагают так, как показано на рис. 14, а, а угловые размеры — как показано на рис. 14, б. Если размерная линия будет находиться в зоне, которая на чертеже заштрихована, размерные числа наносят на полках линий-выносок (рис. 15).
Если для написания размерного числа мало места над размерной линией или это место занято другими элементами изображения и впи-
сать в него размерное число невозможно, размерное число наносят по одному из вариантов, приведенных на рис. 16.
С целью упрощения ряда изображений, создания удобств для чтения чертежа стандарт предусматривает применение условных обозначений в виде букв латинского алфавита и графических знаков, которые ставятся перед размерными числами. На чертежах применяются
знаки и буквы для обозначения диаметра и радиуса, длины дуги и квадрата, уклона и конусности, сферы, толщины и длины детали.
Перед размерным числом диаметра наносится знак 0 (рис. 17). Причем между знаком и числом никаких пропусков не предусмотрено. Для окружностей малого диаметра размерные линии стрелки и сам размер наносят по одному из вариантов, приведенных на рис. 18.
Перед размерным числом радиуса дуги всегда ставится знак в виде прописной латинской буквы R. Размерную линию в этом случае проводят по направлению к центру дуги и ограничивают только одной стрелкой, упирающейся в дугу или ее продолжение (рис. 19). Если величина радиуса на чертеже менее 6 мм, стрелку рекомендуется распо-
лагать с внешней стороны дуги. При необходимости задания положения центра дуги его отмечают пересечением центровых или выносных линий (рис. 20). В тех случаях, когда на чертеже изображена дуга большого радиуса, для которой центр можно не обозначать, размерную линию обрывают, не доводя до центра (рис. 21). Если же в этом случае центр необходимо отметить, допускается приближать его к дуге (рис. 22). Размерная линия в этом случае показывается с изломом 90°, и оба участка размерной линии проводятся параллельно. Не следует располагать на одной прямой размерные линии, выходящие из одного центра и предназначенные для обозначения размерных дуг. Радиусами рекомендуется обозначать дуги до 180°; дуги, величина которых составляет более 180°, обозначаются диаметром.
Знак дуги наносится над размерным числом (рис. 23). Длину дуги задают в линейных единицах, а размерное число, обозначающее дугу, наносится над размерной линией в соответствии с обычными требованиями.
Для простановки размеров квадрата применяют соответствующий знак D, высота которого равна 7 /10 высоты размерного числа (рис. 24, а). При ином расположении квадрата наносят размеры его сторон (рис. 24, б). Следует отметить, что знак квадрата наносят только на том изображении, на котором он проецируется в линию.
Знак конусности поверхности наносится на полке линии-выноски, расположенной параллельно оси конуса или на оси конуса (рис. 25, а). Знак конусности располагают так, чтобы его острый угол был направлен в сторону вершины конуса. Величину конусности определяют отношением разности диаметров двух поперечных сечений конуса к расстоянию между этими сечениями, т. е. k = D — dll, где D — диаметр большого сечения; d — диаметр меньшего сечения; l — расстояние между сечениями. Конусность указывают в виде простого дробного числа (рис. 25, б).
Знак уклона прямой указывают на полке линии-выноски. Уклон i представляет собой тангенс угла между данной прямой и горизонтальной или вертикальной прямой (рис. 26, а). Знак уклона располагается
так, чтобы острый угол его был направлен в сторону уклона прямой (рис. 26, б). Уклон, как и конусность, на чертеже задают простой дробью, в процентах или в промилях.
Для обозначения сферы на чертеже применяют знак диаметра или радиуса. В тех случаях, когда по чертежу сферу трудно отличить от других поверхностей, перед знаком радиуса или диаметра допускается добавлять слово «Сфера». Надпись на чертеже выполняется по типу «Сфера диаметр 17» или «Сфера R10» (рис. 27).
Простые плоские детали изображаются в виде одной проекции. В этих случаях ее толщину обозначают строчной буквой s и надпись на чертеже выполняется по типу s2 и располагается на полке линии-выноски (рис. 28, а). Длину предмета указывают буквой / (рис. 28, б).
Фаски на чертежах наносят двумя линейными размерами (рис. 29, а) или одним линейным и одним угловым (рис. 29, б). В том случае, если
угол наклона образующей конуса равен 45°, применяют упрощенное обозначение фаски, когда размерная линия проводится параллельно оси конуса, а надпись выполняется по типу «2 х 45» (рис. 29, в).
Как найти диаметр окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
[spoiler title=”источники:”]
http://lib.qrz.ru/node/9228
http://skysmart.ru/articles/mathematic/diametr-okruzhnosti
[/spoiler]
Радиус – это отрезок, который соединяет центр окружности с любой точкой, которая лежит на этой окружности. Диаметр равен двум радиусам.
На чертежах радиусы используются для обозначения внутренних и наружных скруглений, криволинейных элементов.
Нанесение размеров согласно ГОСТу
Любой чертеж строится согласно определенным размерам, с учетом принятого масштаба, а также в процессе оформления все имеющие значения размеры выносятся с точностью до миллиметра. По типу все размеры делятся на линейные и угловые. К первым относятся размеры прямонаправленных участков, а ко вторым – размеры, измеряемые в градусах, секундах и минутах. Радиусы и диаметры также относятся к размерам, которые указываются на чертежах. Поэтому их оформление должно соответствовать требованиям ГОСТа.
До 2012 года на территории Российской Федерации действовал ГОСТ 2 307.608 «Нанесение размеров и предельных отклонений», который был заменен на ГОСТ 2.307.2011. Оба документа имеют схожую структуру, но последняя версия стандарта учитывает изменения, которые произошли с начала цифровизации. Среди определений можно встретить «электронную модель изделия» и «электронный макет». Оба документа определяют правила нанесения размеров и максимальные допуски отклонений.
Оба ГОСТ требуют минимального, но достаточного количества размеров. Например, один из размеров замкнутой цепочке наносится справочно, отмечается с помощью знака *.
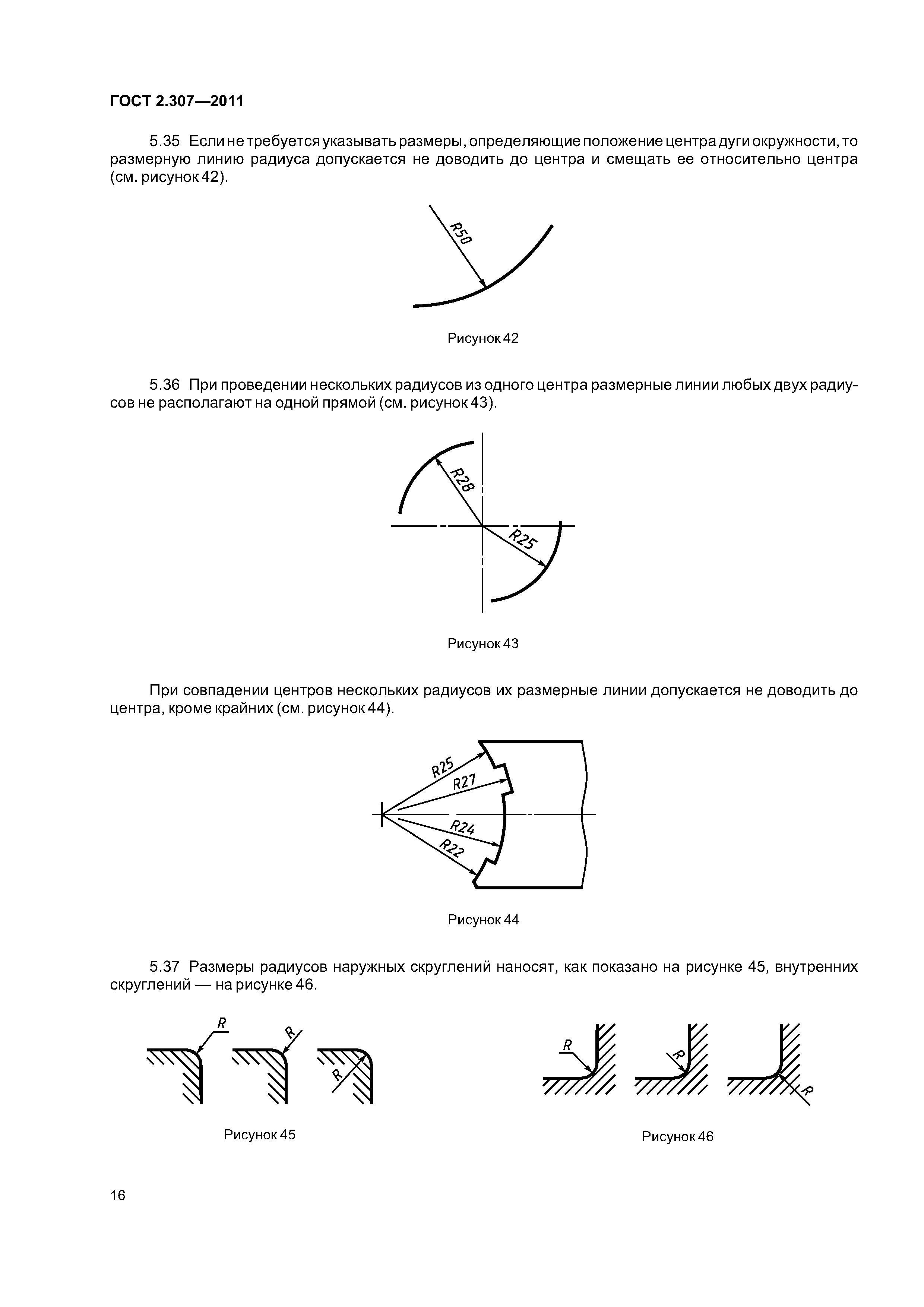
Рисунок 1. ГОСТ 2.307.2011
Радиусы и диаметры на чертеже по ГОСТу
Традиционно, в пояснительных записках и на чертежах используется условное обозначение радиуса латинской буквой R. После этого символа идет размерное число.
Отрезок начинается от центра окружности, на конце отрезка рисуется стрелка, направленная к самой окружности.
Бывают случаи, когда значение радиуса велико и поэтому линию приближают к дуге и показывают с изломом под 90 градусов.
Также зачастую исполнителю нет необходимости показывать центр окружности, особенно если размер очень большой и составляет несколько метров, поэтому сам отрезок не доводят до центра.
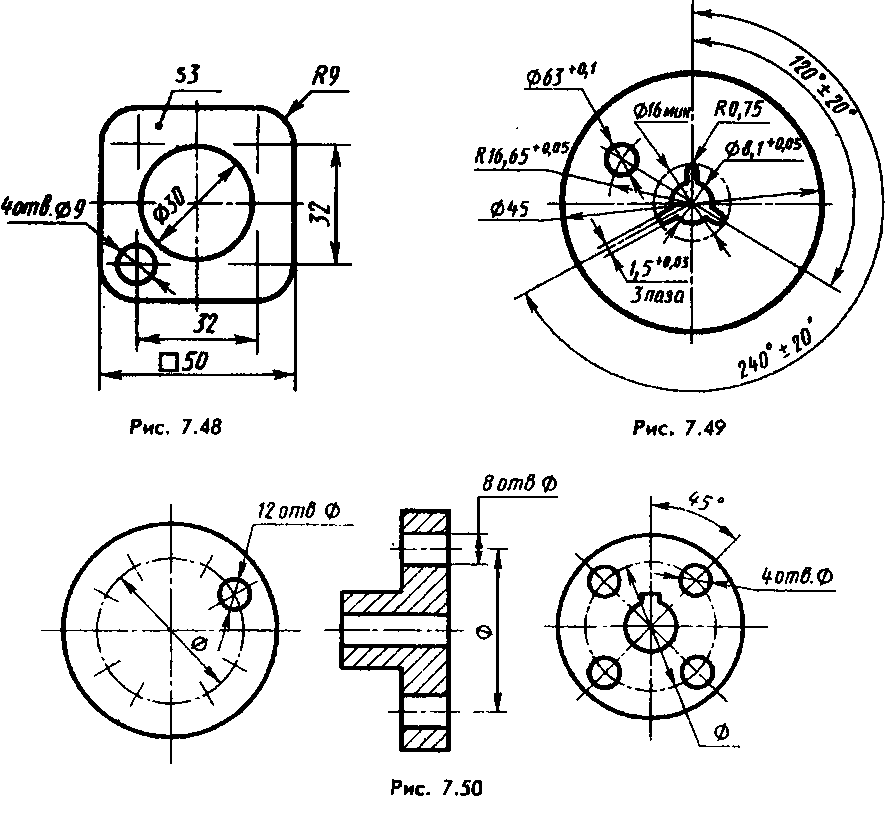
Рисунок 2. Радиусы и диаметры на чертеже по ГОСТу
Как начертить радиус на чертеже
Чтобы начертить радиус на листе необходимо воспользоваться таким инструментом как циркуль. С помощью линейки циркулем отмеряют радиус, размер которого известен заранее. Устанавливают острие циркуля в центр будущей окружности и проводят сектор, часть дуги или окружность целиком в зависимости от условий задачи. Обратным действием можно найти радиус, зная где находится центр окружности. Определить диаметр можно, зная радиус круга, для этого нужно его значение увеличить в два раза. Также, зная длину контура окружности, можно вычислить радиус или диаметр через число Пи.
При построении радиуса на компьютере воспользуемся соответствующим инструментом на панели, обычно можно начертить окружность по заданному центру и значению, начертить сектор или дугу ограничив ее на плоскости. Вводя нужные значения и указав точку на плоскости, программа сама построит окружность по радиусу. Чтобы соединить отрезки с помощью радиуса используется инструмент «Сопряжение». Необходимо выбрать отрезки, а программа сама подберет нужный радиус. Эта функция очень удобна, когда необходимо соединить два элемента, располагающихся под углом, к примеру стены дома на плане или полку и стенку двутавра на чертеже.
Радиусы можно начертить в любой программе векторной графики, начиная от Корел Дро, заканчивая Автокадом, Ревитом, Компасом и Архикадом. Линейный размер наносится после того, как сам элемент вычерчен, через инструмент «Размеры», расположенный в основном меню. Через свойства можно изменить высоту текста, тип оформления концов отрезков, толщину и прочее.

Рисунок 3. Как начертить радиус на чертеже
Как показать несколько радиусов на чертеже
Если из одного центра проводятся несколько радиусов, то согласно принятой практике для простоты прочтения чертежа их не располагают на одной прямой, между ними должен быть угол.
Если необходимо показать несколько линий радиуса, то до центра доводят только крайние радиусы, а остальные остаются укороченными.
В ситуациях, когда применяется большое количество одинаковых радиусов скругления, наносить размеры и показывать условные обозначения не обязательно. В примечаниях указывают всю необходимую информацию, к примеру, что «радиусы скругления составляют 10 мм» или «неуказанные радиусы 7 мм».
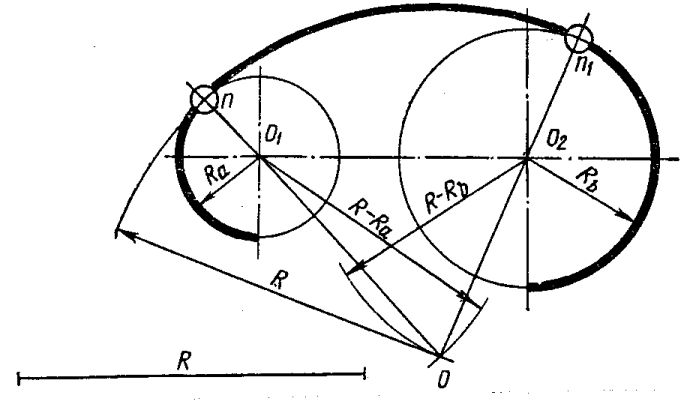
Рисунок 4. Несколько радиусов на чертеже
Как показать радиус отверстия
На машиностроительных, строительных, сборочных чертежах зачастую приходиться изображать отверстия, к примеру, отверстия трубопроводов, имеющих внутреннюю резьбу или же болты, которые имеют наружную резьбу. В этом случае также используется радиус, который позволяет определить точный размер элемента. Малый размер может не позволить уместить всю информацию внутри изображения, поэтому все указания и полки размещают снаружи.
На одном листе показывают вид на разные плоскости проекции, на плане трубы показывается ось, на виде справа или слева, отверстие и его радиус или диаметр.
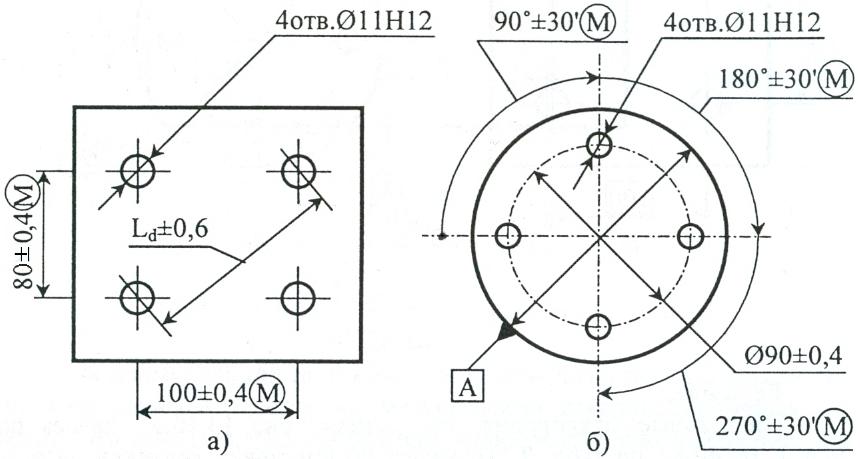
Рисунок 5. Изображение радиуса отверстия на чертеже
Как показать диаметр на чертеже
Диаметр на чертеже обозначается с помощью символа перечеркнутого круга, после которого следует размерное число. Если диаметр элемента меньше 12 мм, то размерное число и стрелка располагаются снаружи. Если размер элемента от 12 до 40 мм, то стрелки, располагают внутри элемента (проходят через центр окружности), а размерные числа выносят наружу. Для диаметра более 40 мм и размерные числа, и стрелки располагают внутри. Чтобы обозначит сферы перед перечёркнутой окружностью наносят еще один круг.
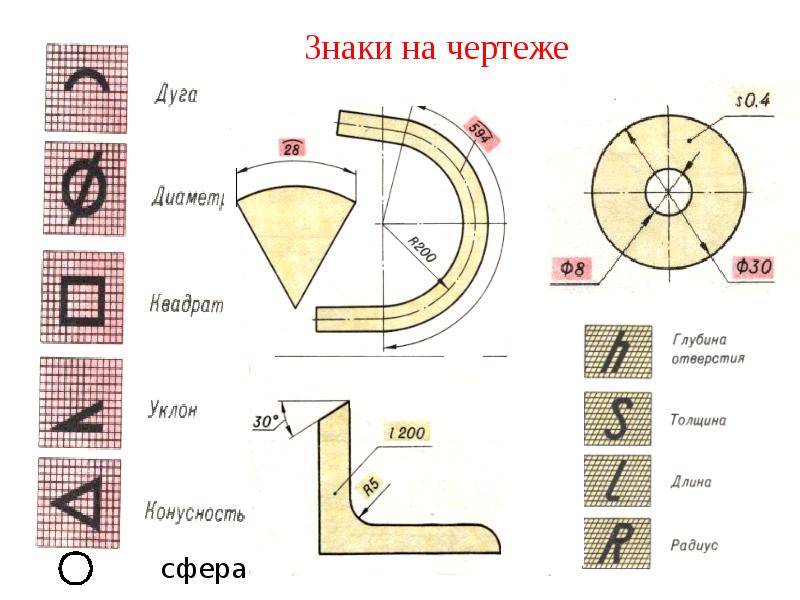
Рисунок 6. Как отметить диаметр на чертеже
Ответы на вопросы
В каком случае допускается не показывать радиус?
Радиус не показывают, если размер скругления в масштабе чертежа равен или менее 1 мм.
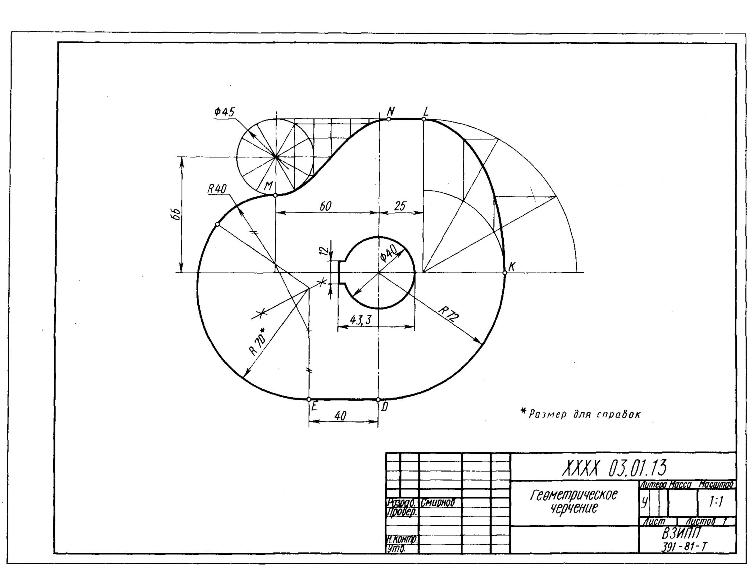
Рисунок 7. Пример обозначения радиусов на чертеже
Как можно упростить обозначение одинаковых радиусов?
Зачастую детали выполняются симметричными, и их скругления имеют одинаковые значения. В этом случае обозначается стрелка для каждого скругления, но все они имеют общую полку, на которой выполняется простановка размерного числа.

Рисунок 8. Одинаковые радиусы
Нужно ли писать единицу измерения после обозначения радиуса?
Радиус, так же, как и ширина, толщина, длина или высота изделия относится к линейным размерам. Согласно требованиям ГОСТа, по умолчанию их наносят в миллиметрах. Соответственно других единицы измерения указывают, если размер определяется в метрах, сантиметрах, дециметрах, футах или иных единицах.
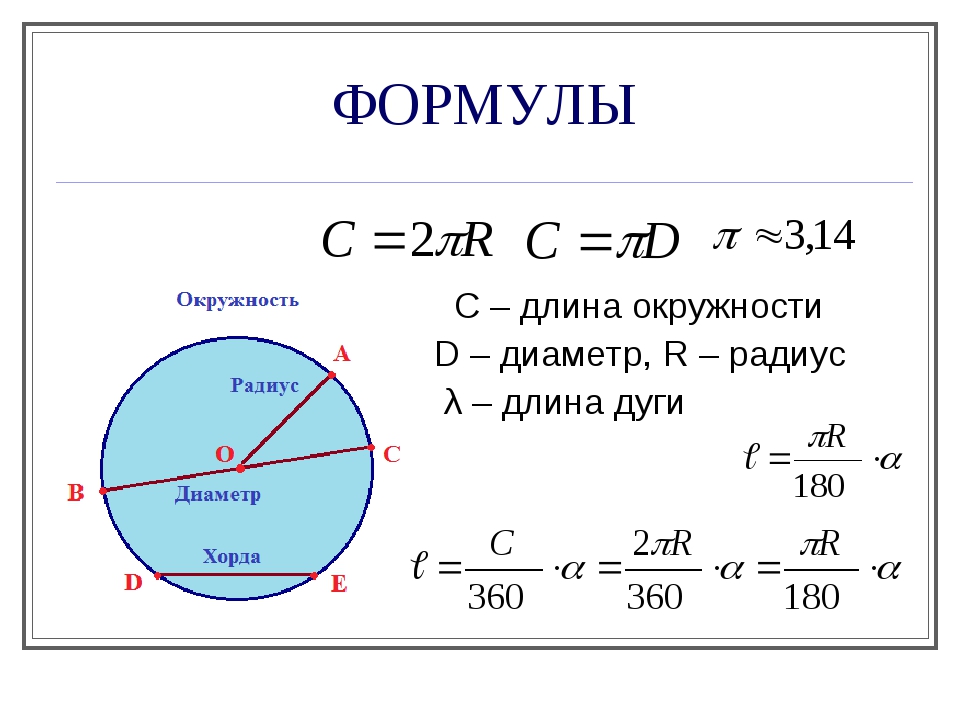
Рисунок 9. Единицы измерения радиуса
Как измерить диаметр с чертежа?
Игра Игра
Ученик
(210),
на голосовании
6 лет назад
Просто линейкой от дочки до точки или еше делить на 2?? Туплю капец.
Голосование за лучший ответ
АНДРЕЙ ШАБАНОВ
Оракул
(66550)
6 лет назад
просто
Сергей К
Просветленный
(30361)
6 лет назад
от точки до точки
Элеонора Смирная Дворкина
Искусственный Интеллект
(443955)
6 лет назад
Просто замерять линейкой от точки до точки.
Bek Madiyar
Знаток
(311)
6 лет назад
отмасштабируй на лист а4 и измерь линейкой
Игра ИграУченик (210)
6 лет назад
так и сделал
Bek Madiyar
Знаток
(311)
Тогда какие вопросы?
Риторика
Иван Непомнящий
Искусственный Интеллект
(177230)
6 лет назад
Можно и на три, если такой масштаб, если масштаба нет то и делить не надо
Похожие вопросы
При
нанесении размера радиуса перед размерным
числом помещают прописную букву R.
Если
при нанесении размера радиуса дуги
окружности необходимо указать размер,
определяющий положение ее центра, то
последний изображают в виде пересечения
центровых или выносных линий.
При
большой величине радиуса центр допускается
приближать к дуге, в этом случае размерную
линию радиуса показывают с изломом под
углом 90° (рис. 4.29).
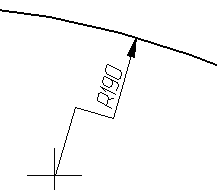
Рис.
4.29
Если
не требуется указывать размеры,
определяющие положение центра дуги
окружности, то размерную линию радиуса
допускается не доводить до центра и
смещать ее относительно центра (рис.
4.30).

Рис.
4.30
При
проведении нескольких радиусов из
одного центра размерные линии любых
двух радиусов не располагают на одной
прямой (рис. 4.31а). При совпадении центров
нескольких радиусов их размерные линии
допускается не доводить до центра, кроме
крайних (рис. 4.31б).
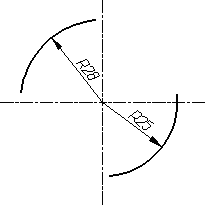
Рис.
4.31а
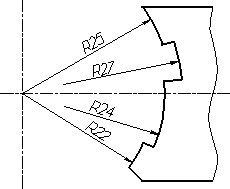
Рис.
4.31б
Размеры
радиусов наружных скруглений наносят,
как показано на рис. 4.32, внутренних
скруглений – на рис. 4.33.

Рис.
4.32
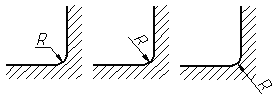
Рис.
4.33
Радиусы
скругления, размер которых в масштабе
чертежа 1 мм и менее, на чертеже не
изображают и размеры их наносят как
показано на рис. 4.34.

Рис.
4.34
Способ
нанесения размерных чисел при различных
положениях размерных линий (стрелок)
на чертеже определяются наибольшим
удобством чтения. Размеры одинаковых
радиусов допускается указывать на общей
полке, как показано на рис. 4.35.
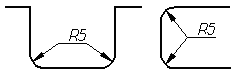
Рис.
4.35
Если
радиусы скруглений, сгибов и т. п. на
всем чертеже одинаковы или какой-либо
радиус является преобладающим, то вместо
нанесения размеров этих радиусов
непосредственно на изображении
рекомендуется в технических требованиях
делать запись типа: «Радиусы скруглений
4 мм»; «Внутренние радиусы сгибов 10мм»;
«Неуказанные радиусы 8 мм» и т.п.
При
указании размера диаметра (во всех
случаях) перед размерным числом наносят
знак « Ø ».
Перед
размерным числом диаметра (радиуса)
сферы так же наносят знак Ø (
R ) без надписи «Сфера» (рис. 4.36).
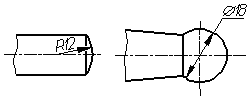
Рис.
4.36
Если
на чертеже трудно отличить сферу от
других поверхностей, то перед размерным
числом диаметра (радиуса) допускается
наносить слово «Сфера» или знак «○»,
например, «Сфера Ø 18,
○ R 12». Диаметр знака сферы равен размеру
размерных чисел на чертеже.
Размеры
квадрата наносят, как показано на рис.
4.37 а, б, в.
Высота
знака « »
должна быть равна высоте размерных
чисел на чертеже.
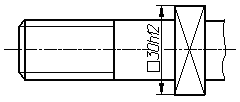
рис.
4.37а

рис.
4.37б

рис.
4.37в
Размер
детали или отверстия прямоугольного
сечения могут быть указанны на полке
линии-выноски размерами сторон через
знак умножения. При этом на первом месте
должен быть указан размер той стороны
прямоугольника, от которой проводиться
линия-выноска (рис. 4.38).
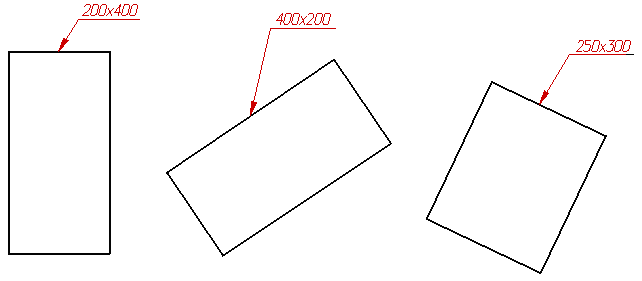
Рис.
4.38
4.3. Конусность, уклоны, фаски
Перед
размерным числом, характеризующим
конусность, наносят знак « ![]() »,
»,
острый угол которого должен быть
направлен в сторону вершины конуса
(рис. 4.39).
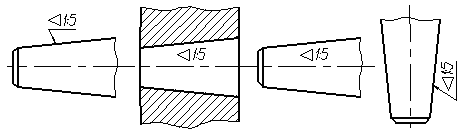
Рис.
4.39
Знак
конуса и конусность в виде соотношения
следует наносить над осевой линией или
на полке линии-выноски.
Уклон поверхности следует
указывать непосредственно у
изображения поверхности уклона
или на полке линии-выноски в виде
соотношения (рис. 4.40а), в процентах (рис.
4.40б) или в промиллях (рис. 4.40в). Перед
размерным числом, определяющим уклон,
наносят знак «>», острый угол которого
должен быть направлен в сторону уклона.

Рис.
4.40а
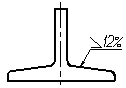
Рис.
4.40б
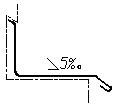
Рис.
4.40в
Отметки
уровней (высоты, глубины) конструкции
или ее элемента от какого-либо отсчетного
уровня, принимаемого за «нулевой» на
виде и разрезе, помещают на выносных
линиях (или на линиях контура) и обозначают
знаком « ↓ », выполненным сплошными
тонкими линиями, длинна штрихов 2-4 мм
под углом 45° к выносной линии или линии
контура (рис. 4.41а), на виде сверху их
следует наносить в рамке непосредственно
на изображении или на линии-выноске
(рис. 4.41б), или как показано на рис. 4.41в.
Отметки уровней указывают в метрах с
точностью до третьего десятичного знака
без обозначения единиц измерения.
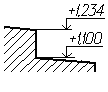
Рис.
4.41а
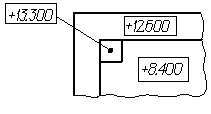
Рис.
4.41б
![]()
Рис.
4.41в
Размеры
фасок под углом 45° наносят, как показано
на рис. 4.42а.
Допускается
указывать размеры не изображенной на
чертеже фаски под углом 45°, размер
которой в масштабе чертежа 1 мм и менее,
на полке линии-выноски, проведенной от
грани (рис. 4.42б).
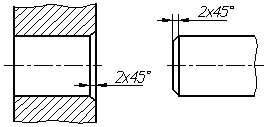
Рис.
4.42а
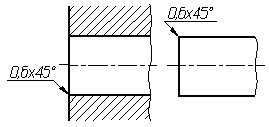
Рис.
4.42б
Размеры
фасок под другими углами указывают по
общим правилам – линейным и угловым
размерами (рис. 4.43 а и б) или двумя
линейными размерами (рис. 4.43в).
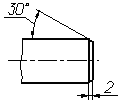
Рис.
4.43а
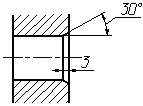
Рис.
4.43б

Рис.
4.43в
Размеры
нескольких одинаковых элементов изделия,
как правило, наносят один раз с указанием
на полке линии-выноски количества этих
элементов (рис. 4.44а). Допускается указывать
количество элементов, как показано на
рис. 4.44б.
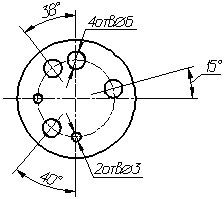
Рис.
4.44а
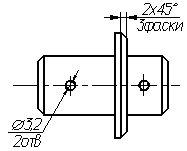
Рис.
4.44б
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Окружность
- Построение окружности циркулем
- Радиус, хорда и диаметр
- Дуга
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:

Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:

Построение окружности циркулем
Для построения окружности используют специальный прибор — циркуль:

Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:

Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:

Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.

Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
D = 2r.
Дуга
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:

Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:

Для обозначения дуг используется символ  :
:
О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.

Хорда AB стягивает дуги  AFB и
AFB и  AJB.
AJB.
