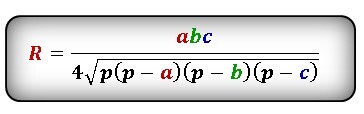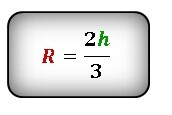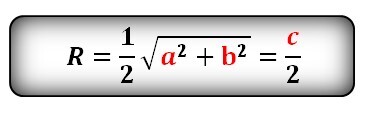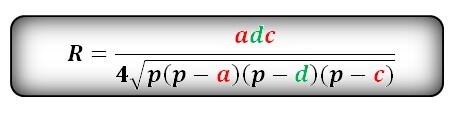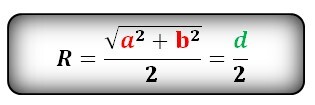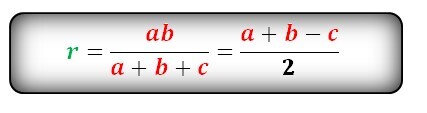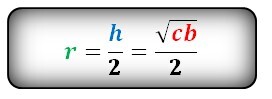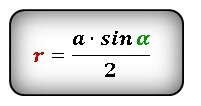Как найти диаметр окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
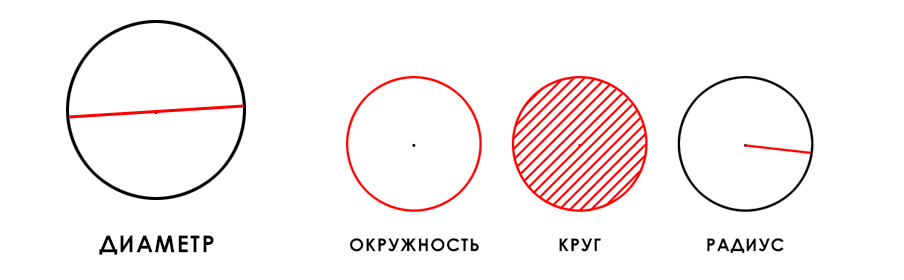
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
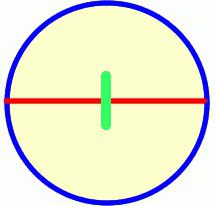
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Как посчитать диаметр окружности
Онлайн калькулятор
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Каков диаметр (d) если длина окружности C?
Формула
d = C /π , где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её радиус r?
Формула
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её площадь S?
Формула
d = √ 4S /π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см 2 , то его диаметр примерно равен 2.52 см.
Как вычислить диаметр окружности?
Для начала, давайте разберемся, что такое окружность и в чем ее отличие от круга. Возьмите ручку или карандаш красного цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, – это окружность. А вот синее содержимое внутри нее – и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус – 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить длину окружности. Формула L = 2 Пи * R, где 2 – это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S – в данном случае площадь фигуры. Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S – площадь заданного треугольника, а p – периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении размера кольца, что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
[spoiler title=”источники:”]
http://poschitat.online/diametr-okruzhnosti
http://fb.ru/article/64066/kak-vyichislit-diametr-okrujnosti
[/spoiler]
Как найти диаметр окружности равнобедренного треугольника(см)?
Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Решить задание можно несколькими способами. Можно исходить из теоремы косинусов,
Далее по теореме синусов считаем диаметр.
Можно считать и по другой схеме. Не через вычисление основания — с, а через угол при основании.
Есть и еще один вариант решения задачи.
Диаметр окружности описанной около равнобедренного треугольника находится по формуле: сторона делённая на синус угла противолежащего этой стороне.
Берём угол 120 градусов, синус 120 градусов равен синус 60 градусов, и равен корень из 3 делить на 2. По теореме косинусов можем найти противолежащую сторону. Получили что сторона равна корень из 48. Тогда делим корень из 48 на синус угла 120 градусов и получаем 8 см.
Теорема синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, воспользуемся правилом пропорции и получим:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
,где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Для остроугольного треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Для тупоугольного треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
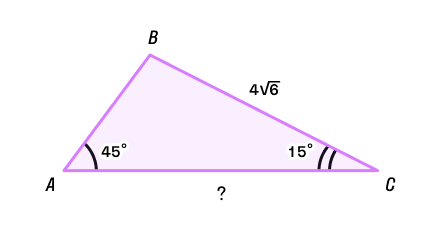
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Сторону AC найдем по теореме синусов:
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см соответственно. Найти угол, который расположен напротив данного катета.
Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Радиус описанной и вписанной окружности: Формулы и примеры
На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.
Что такое радиус
И действительно:
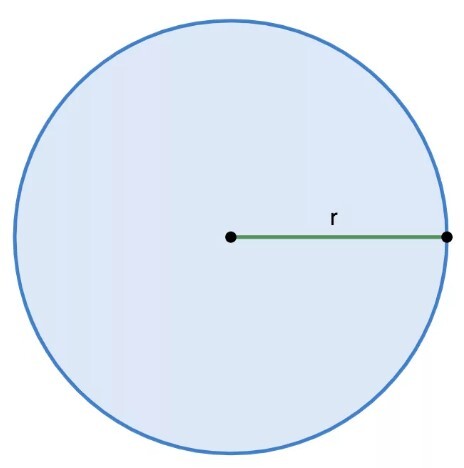
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.
Вот так это выглядит графически.
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
- В анатомии этим словом обозначают Лучевую кость предплечья.
Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
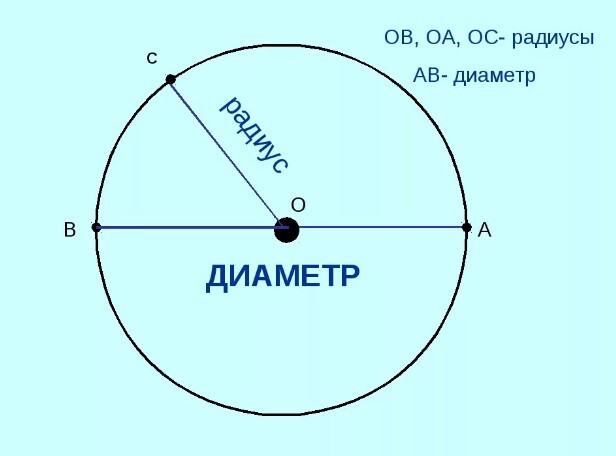
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
Длина диаметра равна удвоенной длине радиуса.
Примеры задач
Длина окружности равняется 87,92 см. Найдите ее радиус.
Используем первую формулу (через периметр):
Найдите радиус круга, если его площадь составляет 254,34 см 2.
Воспользуемся формулой, выраженной через площадь фигуры:
Формулы для радиуса описанной окружности
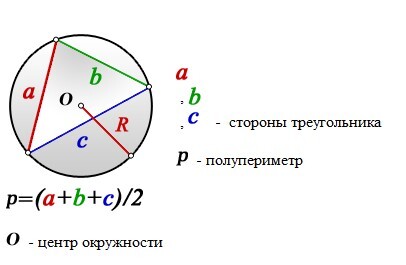
Найти радиус описанной окружности треугольника по сторонам
Формула радиуса описанной окружности треугольника (R ) :
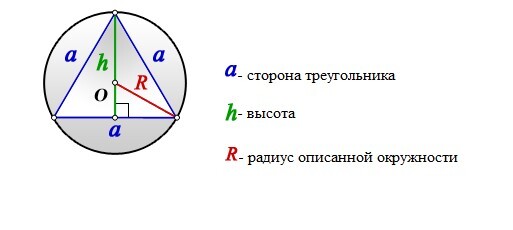
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Формула радиуса описанной окружности равностороннего треугольника через высоту:
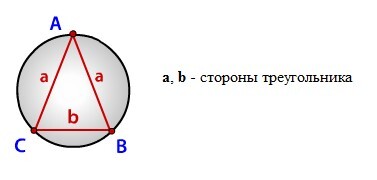
Найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
Формула радиуса описанной окружности равнобедренного треугольника (R):
Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
Формула радиуса описанной окружности прямоугольного треугольника (R):
Радиус описанной окружности трапеции по сторонам и диагонали
Формула радиуса описанной окружности равнобокой трапеции, (R)
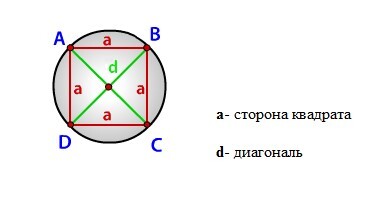
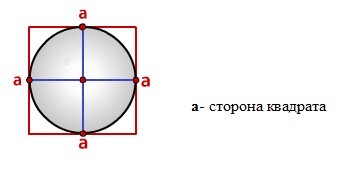
Найти радиус описанной окружности около квадрата
Радиус описанной окружности квадрата равен половине его диагонали
Формула радиуса описанной окружности квадрата (R):
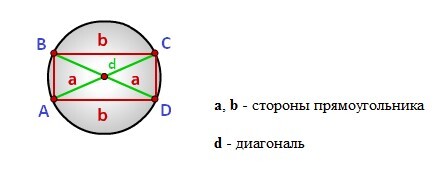
Радиус описанной окружности прямоугольника по сторонам
Радиус описанной окружности прямоугольника равен половине его диагонали
Формула радиуса описанной окружности прямоугольника (R):
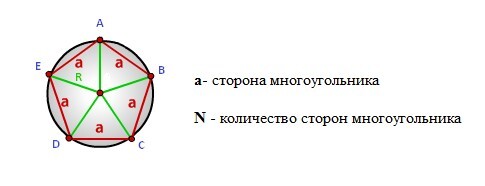
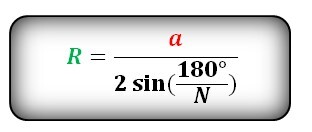
Радиус описанной окружности правильного многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
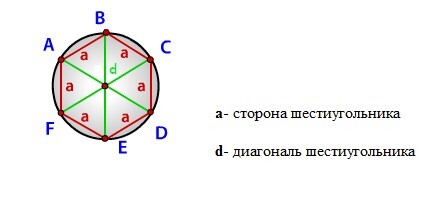
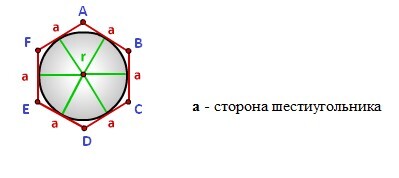
Радиус описанной окружности правильного шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
Формула радиуса вписанной окружности в треугольник (r):
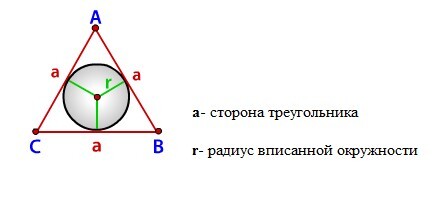
Радиус вписанной окружности в равносторонний треугольник
Формула для радиуса вписанной окружности в равносторонний треугольник (r):
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны (r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол (r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту (r ) :
Радиус вписанной окружности в прямоугольный треугольник
Формула радиуса вписанной окружности в прямоугольный треугольник (r):
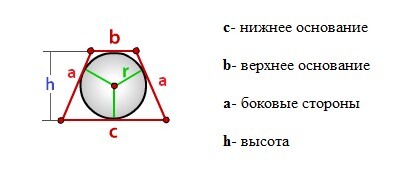
Радиус вписанной окружности в равнобочную трапецию
Формула радиуса вписанной окружности равнобочной трапеции (r):
Радиус вписанной окружности в квадрат
Формула радиуса вписанной окружности в квадрат (r):
Радиус вписанной окружности в ромб
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
Формула радиуса вписанной окружности в ромб через диагонали (r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол (r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол (r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону (r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
Формула радиуса вписанной окружности в ромб (r ) :
Радиус вписанной окружности в правильный многоугольник
Формула радиуса вписанной окружности в правильный многоугольник, (r):
Радиус вписанной окружности в шестиугольник
Формула радиуса вписанной окружности в шестиугольник, (r):
Примеры задач
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:
Остается только применить соответствующую формулу для вычисления радиуса круга:
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Воспользуемся подходящей формулой, подставив в нее известные значения:
Всем спасибо и приятного просмотра! Если понравилась публикация подписывайтесь и ставьте палец вверх!
|
Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника. Решить задание можно несколькими способами. Можно исходить из теоремы косинусов, Далее по теореме синусов считаем диаметр. Можно считать и по другой схеме. Не через вычисление основания – с, а через угол при основании. Есть и еще один вариант решения задачи. Ответ: 8см. автор вопроса выбрал этот ответ лучшим Артём1234567897012 3 года назад Диаметр окружности описанной около равнобедренного треугольника находится по формуле: сторона делённая на синус угла противолежащего этой стороне. Берём угол 120 градусов, синус 120 градусов равен синус 60 градусов, и равен корень из 3 делить на 2. По теореме косинусов можем найти противолежащую сторону. Получили что сторона равна корень из 48. Тогда делим корень из 48 на синус угла 120 градусов и получаем 8 см. Знаете ответ? |
как найти диаметр окружности, описывающей треугольник????
Александр
Профи
(680),
на голосовании
14 лет назад
Дополнен 14 лет назад
хрен найдёшь!
Голосование за лучший ответ
Нина Богодарова
Мастер
(1630)
14 лет назад
Взять учебник геометрии найти формулу для радиуса описанной окружности найти радиус по этой формуле и умножить его на 2 – получишь диаметр.
imba
Гуру
(2592)
14 лет назад
диаметр это есть сумма 2 радиусов, а радуис описанной окр. равна
=abc/4S
Анастасия
Ученик
(104)
1 год назад
Найдите диаметр окружности треугольника
Похожие вопросы
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое диаметр круга?
Диаметр круга – это отрезок, соединяющий две точки на окружности и проходящий через центр круга.
Если же говорить, про другие фигуры, то диаметром называется максимальное расстояние между точками этой фигуры. Диаметр круга – не исключение, так как это самый длинный отрезок, который можно провести в границах окружности.
Если нарисовать диаметр, то он будет выглядеть следующим образом (выделен красным на рисунке ниже).
Теперь давайте рассмотрим, как можно найти диаметр и какие для этого существуют формулы.
Формулы определения диаметра круга
Для определения диаметра существует несколько разных способов в зависимости от известных частей круга.
По радиусу
Самая простая формула определения диаметра может быть использована, если известен радиус круга. Радиус — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности. Диаметр равен двум радиусам.
d = r × 2
Где d – это диаметр, а r – радиус.
По длине окружности
Второй способ нахождения диаметра можно использовать тогда, когда известна длина окружности. Окружность — это замкнутая плоская кривая, все точки которой равноудалены от центра. Тако вот, диаметр равен длине окружности, делённой на число Пи.
d = L / π
Где d – это диаметр, а L – длина окружности, а π – константа, равная 3,14.
Эта формула, основывает на том, что отношение длины окружности к её диаметру всегда является постоянным числом, которое равняется примерно 3,14 и называется π (пи).
Через площадь круга
Чуть более изощренной и сложной является формула вычисления диаметра через площадь круга. Чаще всего требуется, наоборот, посчитать площадь круга, если известен диметр. Но если задача стоит обратная, то формула расчёта будет выглядеть следующим образом:
d = 2 × (S/π)1/2
Где d – диаметр, S – площадь круга, а π – константа, которая примерно равна 3,14.
То есть диаметр равен удвоенному корню частного площади круга к числу пи. Стоит отметить, что корень и степень ½ – это одно и то же.
Примеры вычисления диаметра
Давайте для закрепления рассмотрим несколько примеров.
Пример 1. Диаметр по длине окружности трубы 🚿
Предположим, у вас под рукой не оказалось штангенциркуля (устройства для измерения ширины изделий).
А вам требуется рассчитать диаметр действующей трубы, конца которой не видно. Для этого с помощью рулетки или сантиметра, вы можете измерить длину окружности, просто обернув рулетку вокруг трубы. А потом эту длину нужно будет разделить на 3,14. Если длина окружности трубы оказалась 31,4 сантиметра, тогда диаметр будет равен частному этой длинны к числу Пи, то есть:
d = 31,4 / 3,14 = 10 см.
Это и есть правильный ответ – 10 сантиметров.
Пример 2. Диаметр по колеса радиусу 🚲
Тут всё гораздо проще. Предположим, что вы знаете радиус колеса велосипеда – 10 дюймов. Какой будет диаметр?
Диаметру будет равен двум радиусам, то есть 20 дюймов.
Кстати, для справки, 1 дюйм = 2,54 сантиметра. То есть 10 дюймов = 25,4 сантиметра. В итоге диаметр колеса равен: 2 × 25,4 = 50,8 см.
❓Вопросы и ответы
И конечно же обратите внимание на ответы на часто задаваемые вопросы относительно расчёта длины диаметра круга.
Как работает ваш онлайн-калькулятор?
Просто. Вы выбираете, что известно: радиус, длина окружности или площадь круга (1), затем вписываете известное значение (2), выбираете размерность из мм, см, м, км (3) и нажимаете кнопку «рассчитать»?
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть различные калькуляторы, в частности калькуляторы: площади круга, длины окружности и диаметра. Для последнего калькулятор находится на данной странице.
Достаточно ли у меня данных для расчёта?
Для вычисления диаметра круга нужно что-то одно: радиус, длина окружности или площадь круга. Остальное вычислит наш калькулятор по специальным формулам, которые описаны выше.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Если у автомобильного колеса параметр R16, то какой у него диаметр?
16 дюймов, а радиус 8 дюймов. Как ни странно, диаметр такого колеса (точнее диска колеса) составляет 16 дюймов, то есть 40,64 см. Очень часто люди называют радиус в качестве единицы измерения: мол, радиус 16 дюймов. Но тогда представьте, для какого трактора диаметр диска будет более 80 сантиметров.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии