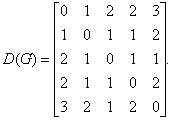С помощью алгоритма фронта волны найти расстояния в ориентированном графе D: диаметр, радиус и центры.
Пусть ориентированный граф с n³2 вершинами и V,W (V¹W) – заданные вершины из V.
Алгоритм поиска минимального пути из в
в ориентированном графе
(Алгоритм фронта волны).
1) Помечаем вершину индексом 0, затем помечаем вершины Î образу вершины
индексом 1. Обозначаем их FW1 (V). Полагаем K=1.
2) Если или K=N-1, и одновременно
то вершина
не достижима из
. Работа алгоритма заканчивается.
В противном случае продолжаем:
3) Если , то переходим к шагу 4.
В противном случае мы нашли минимальный путь из в
и его длина равна K. Последовательность вершин
Есть этот минимальный путь. Работа завершается.
4) Помечаем индексом K+1 все непомеченные вершины, которые принадлежат образу множества вершин c индексом K. Множество вершин с индексом K+1 обозначаем . Присваиваем K:=K+1 и переходим к 2).
Замечания
· Множество называется фронтом волны KГо уровня.
· Вершины могут быть выделены неоднозначно, что соответствует случаю, если
несколько минимальных путей из
в
.
Чтобы найти расстояния в ориентированном графе, необходимо составить матрицу расстояний R(D) между его вершинами. Это квадратная матрица размерности , элементы главной диагонали которой равны нулю (
, I=1,..,N).
Сначала составляем матрицу смежности. Затем переносим единицы из матрицы смежности в матрицу минимальных расстояний (, если
). Далее построчно заполняем матрицу следующим образом.
Рассматриваем первую строку, в которой есть единицы. Пусть это строка − I-тая и на пересечении с J-тым столбцом стоит единица (то есть ). Это значит, что из вершины
можно попасть в вершину
за один шаг. Рассматриваем J-тую сроку (строку стоит вводить в рассмотрение, если она содержит хотя бы одну единицу). Пусть элемент
. Тогда из вершины
в вершину
можно попасть за два шага. Таким образом, можно записать
. Следует заметить, что если в рассматриваемых строках две или более единиц, то следует прорабатывать все возможные варианты попадания из одной вершины в другую, записывая в матрицу длину наикратчайшего из них.
Примечание. Самый длинный путь найти при помощи алгоритма фронта волны.
Пример
Найдем расстояния в ориентированном графе D, изображенном на рис. 7. В данной задаче количество вершин N=7, следовательно, матрицы смежности и минимальных расстояний между вершинами ориентированного графа D Будут иметь размерность 7×7.
Рис.7.
Матрица смежности:

Начинаем заполнять матрицу R(D) минимальных расстояний: сначала ставим нули по главной диагонали и Rij=Aij, если Aij=1, (т. е. переносим единицы из матрицы смежности). Рассматриваем первую строку. Здесь есть две единицы, то есть из первой вершины за один шаг можно попасть во вторую и шестую. Из второй вершины можно попасть за один шаг в третью (путь в первую вершину нас не интересует), следовательно, можно записать . Из шестой вершины можем добраться за один шаг в пятую и седьмую, а значит,
,
. Теперь ищем маршруты, исходящие из первой вершины, состоящие из 3 шагов: за 2 шага идем в третью вершину, оттуда за один шаг попадаем в четвертую, поэтому
. В итоге получаем следующую матрицу:

Таким образом, диаметром исследуемого ориентированного графа будет .
Для каждой вершины заданного ориентированного графа найдем максимальное удаление (эксцентриситет) в графе G от вершины нее по формуле, которая была приведена выше : R(Vi) − максимальное из расстояний, стоящих в I-той строке. Таким образом,
R(V1)=3, R(V2)=3, R(V3)=5, r(V4)=4, r(V5)=2, r(V6)=2, r(V7)=3.
Значит, радиусом графа G будет
Соответственно, центрами графа G Будут вершины V5 и V6 , так как величины их эксцентриситетов совпадают с величиной радиуса.
Опишем теперь нахождение минимального пути из вершины V3 в вершину V6 по алгоритму фронта волны. Обозначим вершину V3 как V0, а вершину V6 – как W (см. рис. 8).
Рис.8.
Множество вершин, принадлежащих образу V0, состоит из одного элемента – это вершина V4, которую, согласно алгоритму, обозначаем как V1: FW1(V3)={V4}. Поскольку искомая вершина не принадлежит фронту волны первого уровня , продолжаем работу алгоритма. Строим фронт волны второго уровня – это множество вершин, принадлежащих образу вершины V1: FW2(V3)={V7}, обозначаем V7≡V2. В образ вершины V2 входят две вершины – V5 и V4, но, так как V4 уже была помечена как V0, то фронт волны третьего уровня состоит из одного элемента: FW3(V3)={V5}, V5≡V3. Из непомеченных вершин в образ вершины V3 входят V1 и V2, соответственно, FW4(V3)={V1, V2}, V1≡V4, V2≡V4. Теперь помечены все вершины, кроме V6, которая входит в образ вершины
, то есть FW5(V3)={V6≡W}, работа алгоритма закончена. Минимальный путь (5 шагов) из вершины V3 в вершину V6: V3 V4 V7 V5 V1 V6.
| < Предыдущая | Следующая > |
|---|

Теорема 6.7 (Дирака). Если в простом графе с n вершинами, причем n ≥ 3, выполняется условие ρ(v) ≥ n 2 для любой верши-
ны v, то граф G является гамильтоновым.
Теорема 6.8 (Оре). Пусть n – количество вершин в данном графе. Если для любой пары несмежных вершин vi, vj выполнено неравенство d(vi) + d(vj) ≥ n, то граф является гамильтоновым.
Однако существуют и гамильнотовы графы, не являющиеся графами Оре или Дирака.
В некоторых задачах дополнительно используется условие Поша, которое в данном пособии не рассматривается.
6.5.1. Основные определения
Расстоянием d между вершинами vi и vj называется длина минимального пути между этими вершинами.
Диаметром δ связного графа G называется максимальное возможное расстояние между любыми двумя его вершинами.
Для несвязных графов диаметр полагается равным бесконечности.
Центром графа G называется такая вершина v, что максимальное расстояние между v и любой другой вершиной является наименьшим из всех возможных. Это расстояние называется радиусом r. Таким образом,
|
r = min(max d (v1 , v2 )) , |
|
|
v1 |
v2 |
где d (v1 , v2 ) – расстояние между v1 и v2.
6.5.2. Алгоритм нахождения диаметра
Процесс нахождения диаметра графа представляет собой, по сути, полный перебор.
170
Сначала необходимо по всем парам вершин вычислить расстояние, а затем найти максимум из этого множества чисел.
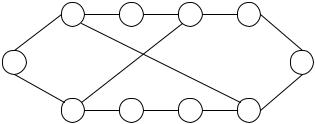
Задача 6.6. Для графа на рис. 6.25 соответствующие расстояния представлены в табл. 6.5.
|
2 |
3 |
4 |
5 |
|
|
1 |
6 |
|||
|
Рис. 6.25 |
10 |
9 |
8 |
7 |
Решение. Представлено в табл. 6.5.
|
Таблица 6.5 |
||||||||||||
|
Матрица расстояний |
||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||
|
1 |
1 |
2 |
2 |
3 |
3 |
2 |
3 |
2 |
1 |
|||
|
2 |
1 |
2 |
3 |
2 |
1 |
2 |
3 |
2 |
||||
|
3 |
1 |
2 |
3 |
2 |
3 |
3 |
2 |
|||||
|
4 |
1 |
2 |
3 |
3 |
2 |
1 |
||||||
|
5 |
1 |
2 |
3 |
3 |
2 |
|||||||
|
6 |
1 |
2 |
3 |
3 |
||||||||
|
7 |
1 |
2 |
3 |
|||||||||
|
8 |
1 |
2 |
||||||||||
|
9 |
1 |
|||||||||||
|
10 |
Необходимо быть аккуратным при вычислении расстояний, например, расстояние между 1-й и 4-й вершинами равно двум, так как помимо пути (1-2-3-4), имеющего длину 3, также существует путь (1-10-4), имеющий длину 2.
Среди всех значений согласно определению диаметра выбирается наибольшее, в данном случае диаметр равен трем.
171

6.5.3. Поиск диаметра при операциях над графами
При операциях над графами иногда значение диаметра проще найти, рассматривая по отдельности участвующие в операциях графы. При этом всегда надо помнить, что диаметр любого несвязного графа равен бесконечности.
При операциях объединения по этой причине в случае отсутствия общих вершин диаметр равен всегда бесконечности. При наличии одной общей вершины значение диаметра вычисляется как сумма диаметров двух участвующих в объединении графов. В более сложных случаях необходимо рисовать полученный граф и анализировать его. Важно помнить, что если в задаче не указано, сколько общих вершин имеют объединяемые графы, то необходимо рассматривать все случаи.
Задача 6.7. Найти значение диаметра графа, полученного в результате объединения простого цикла на 7 вершинах и полного графа на 5 вершинах, если известно, что они имеют 1 общую вершину.
Решение. См. рис. 6.26.
Диаметр простого цикла на 7 вершинах равен [7/2] = 3, а диаметр полного графа всегда равен 1. Значит, диаметр полученного в результате объединения графа равен 3+1 = 4.
При операциях сложения двух графов в случае отсутствия общих вершин диаметр всегда будет не более двух. Это связано с тем, что
172
Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w).
Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w. Это расстояние удовлетворяет аксиомам метрики:
1) d(v, w) 0, причем d(v, w) = 0 тогда и только тогда, когда v=w;
2) d(v, w) = d(w, v);
3) d(v, w) d(v, u) + d(u, w).
Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.
Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
Пример 82.
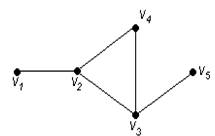
Для графа G, изображенного на рис. 3.16, найти радиус, диаметр и центры.
Рис. 3.16. Граф для примера 82
Решение.
Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами dij которой будут расстояния между вершинами vi и vj. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали.
С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения: для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4.
I know I’m a year late to the thread, but I don’t believe any of these answers are correct. OP mentioned in the comments that the edges are unweighted; in this case, the best algorithm runs in O(nω log n) time (where ω is the exponent for matrix multiplication; currently upper bounded at 2.373 by Virginia Williams).
The algorithm exploits the following property of unweighted graphs. Let A be the adjacency matrix of the graph with an added self-loop for each node. Then (Ak)ij is nonzero iff d(i, j) ≤ k. We can use this fact to find the graph diameter by computing log n values of Ak.
Here’s how the algorithm works: let A be the adjacency matrix of the graph with an added self loop for each node. Set M0 = A. While Mk contains at least one zero, compute Mk+1 = Mk2.
Eventually, you find a matrix MK with all nonzero entries. We know that K ≤ log n by the property discussed above; therefore, we have performed matrix multiplication only O(log n) times so far. We can now continue by binary searching between MK = A2K and MK-1 = A2K-1. Set B = MK-1 as follows.
Set DIAMETER = 2k-1. For i = (K-2 … 0), perform the following test:
Multiply B by Mi and check the resulting matrix for zeroes. If we find any zeroes, then set B to this matrix product, and add 2i to DIAMETER. Otherwise, do nothing.
Finally, return DIAMETER.
As a minor implementation detail, it might be necessary to set all nonzero entries in a matrix to 1 after each matrix multiplication is performed, so that the values don’t get too large and unwieldy to write down in a small amount of time.
Определение
Эксцентриситетом вершины называется расстояние до самой дальней вершины графа.
Радиусом графа называется минимальный эксцентриситет среди всех вершин графа
Диаметром графа – это наибольшее расстояние между всеми парами вершин графа
Центральной вершиной графа является вершина чей эксцентриситет равен радиусу графа.
Периферийной вершиной графа является вершина чей эксцентриситет равен диаметру графа.
Поиск радиуса и диаметра
Сервис граф онлайн позволит вам найти радиус и диаметр, а также укажет центральные и периферийные вершины. Для этого выберете пункт меню Алгоритмы -> Поиск радиуса и диаметра графа.
Реализацию алгоритма на JavaScript можно найти по ссылке: http://graphonline.ru/script/plugins/RadiusAndDiameter.js