Как найти диаметр оси

На этой странице вы узнаете

• Как вода в кружке иллюстрирует сечение цилиндра?
• Как лист бумаги превратить в цилиндр?

Что общего у джентльмена 19 века, Вилли Вонка из «Чарли и шоколадная фабрика», Шерлока Холмса в экранизации «Безобразная невеста» и некоторых сценических костюмов? Цилиндр! О нем, вернее о фигуре цилиндра и поговорим в статье.

Понятие цилиндра

Сейчас мы говорим про мужской головной убор, который был популярен в 19 веке и стал достаточно узнаваем в массовой культуре. Оказывается, в математике также существует цилиндр. И они похожи по форме.

Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. 

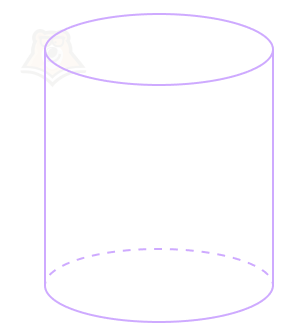
Возможно, для уточнения некоторых терминов вам захочется заглянуть в статью «Тела вращения». 

Если посмотреть на форму шляпы, то она действительно будет похожа на геометрическую фигуру.  Встретить цилиндр можно и в наше время. Обычная кружка является цилиндром.

Прямая, вокруг которой мы крутили прямоугольник, чтобы получить цилиндр, — это ось цилиндра. 

Также, как у Земли есть ось вращения, она есть и у цилиндра. 

Наша кружка стоит на круглом дне. Это дно, как и самый верх кружки, будут называться основаниями цилиндра. 

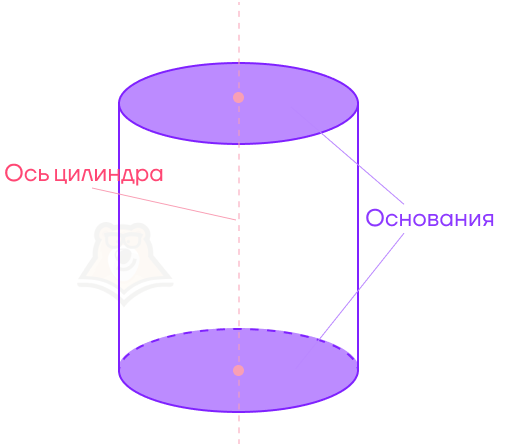
Снова посмотрим на стенки кружки. В цилиндре эта поверхность будет называться цилиндрической поверхностью. Ее также могут называть боковой поверхностью цилиндра. 

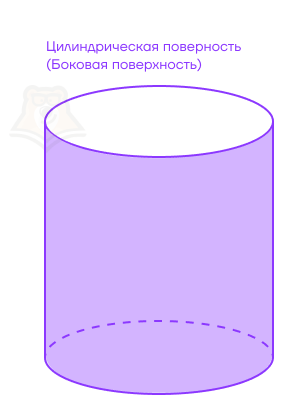
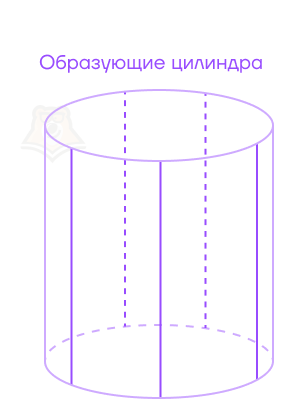
Представим, что наша кружка раскрашена вертикальными линиями. Эти линии будут лежать на цилиндрической поверхности и перпендикулярны основаниям. У них есть название:

Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. 

Все образующие, — а в цилиндре их очень-очень много, —лежат только на цилиндрической поверхности. Эта поверхность и состоит из множества образующих. 

Узнаем ширину кружки. Для этого нужно измерить радиус дна. Этот же радиус будет радиусом основания, а в цилиндре он называется радиусом цилиндра. 

Теперь найдем высоту кружки. Для этого нужно измерить расстояние от дна до самого верха кружки. 

В математике это будет расстоянием между плоскостями, а ищется оно как длина перпендикуляра, опущенного из одной плоскости на другую. Подробнее про это можно прочесть в статье «Расстояния между фигурами». 

Высота цилиндра — перпендикуляр, опущенный из плоскости одного основания на плоскость второго основания. 

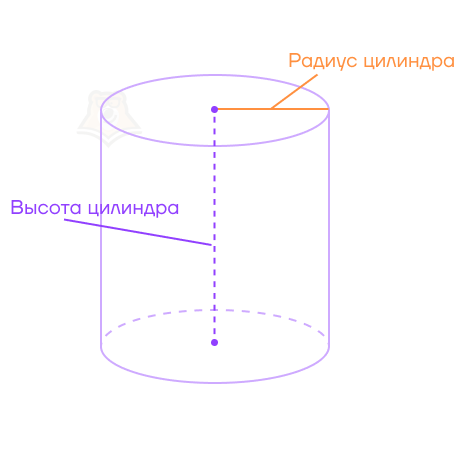
Свойства цилиндра

Рассмотрим, какими свойствами обладает цилиндр. 

Свойство 1. Основания цилиндра равны и параллельны. 

Это всегда два равных круга, лежащих в параллельных плоскостях. 

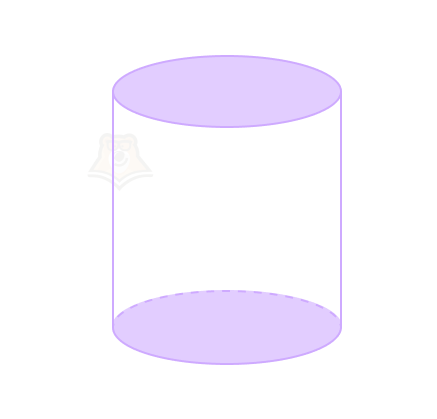
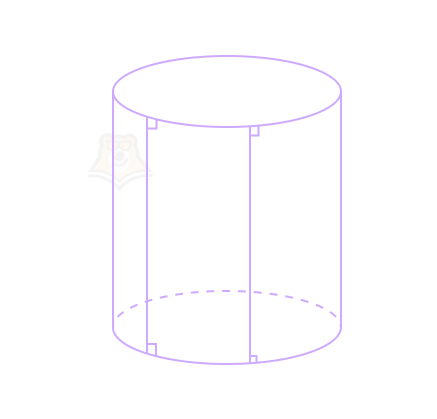
Свойство 2. Образующие цилиндра равны и параллельны. 

Поскольку все образующие перпендикулярны основаниям, то они параллельны между собой по свойству прямой и перпендикулярной ей плоскости. Подробнее про это свойство можно прочесть в статье «Углы в пространстве». 

А равны они потому, что являются перпендикуляром к основаниям, то есть равны высоте цилиндра.

Свойство 3. Сечение цилиндра, проходящее через ось цилиндра, является прямоугольником. Такое сечение в цилиндре будет называться осевым сечением цилиндра. 

Например, если разрезать тортик по диаметру, то место среза как раз будет прямоугольником. 

Подробности про сечения фигур можно найти в статье «Сечения». 

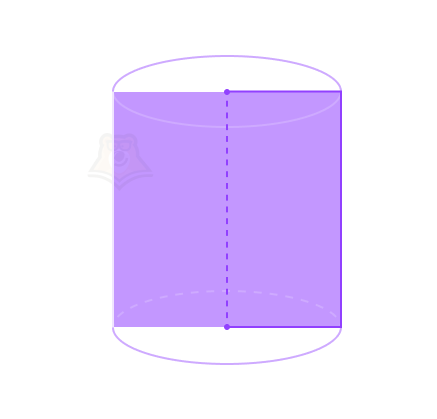
Свойство 4. Сечение цилиндра, проходящее параллельно оси цилиндра и перпендикулярно его основаниям, будет являться прямоугольником. 

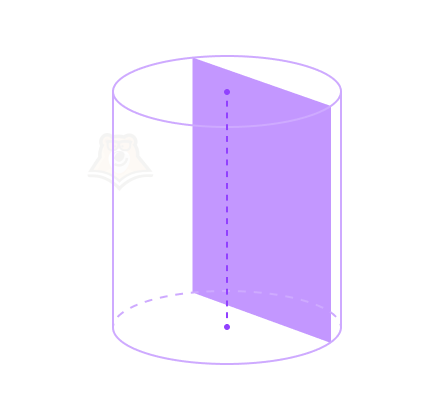
Свойство 5. Сечение цилиндра, перпендикулярное оси цилиндра, является кругом с радиусом, равным радиусу цилиндра. Такое сечение в цилиндре называется перпендикулярным сечением цилиндра. 

Заметим, что все вышеописанные свойства относятся к прямому цилиндру. 

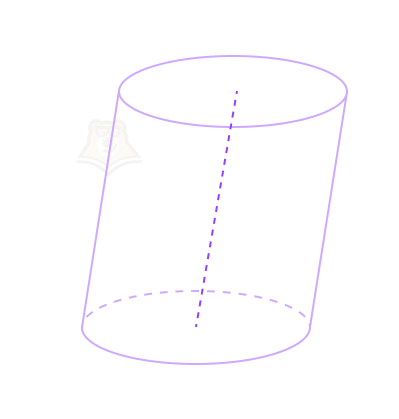
Цилиндр также может быть наклонным. В этом случае ось цилиндра и его образующие не будут перпендикулярны основаниям. 

Если мы разрежем поверхность цилиндра по одной из его образующих и как бы “развернем” ее, у нас получится прямоугольник. 

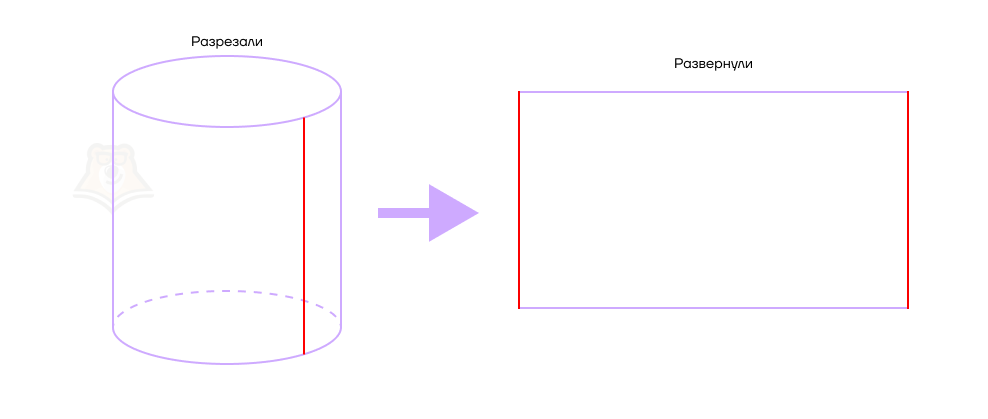
Это также легко увидеть, если вспомнить художников с тубусами. Тубус имеет форму цилиндра, и свернутый прямоугольный лист принимает такую же форму. 

Развертка боковой поверхности цилиндра — прямоугольник, одна сторона которого равна высоте цилиндра, а вторая — длине окружности его основания. 

Формулы цилиндра

А если это прямоугольник, то мы знаем, как найти его площадь. Нам нужно умножить его длину на высоту. Так мы получаем площадь боковой поверхности цилиндра. 

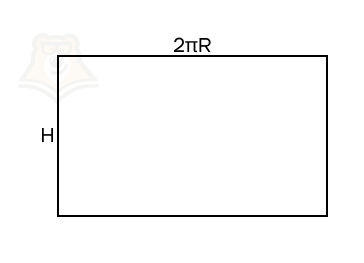
(S_{бок.} = 2 pi RH)

В этой формуле 2R — длина окружности основания, где R — его радиус, а Н — образующая (или высота) цилиндра. Подробнее про площадь прямоугольника и длину окружности (а также про площадь круга) можно прочесть в статьях «Параллелограмм» и «Окружность и круг». 

Мы нашли площадь боковой поверхности. Как же теперь найти площадь полной поверхности?

Для этого нужно сложить площади боковой поверхности и оснований. Следовательно, мы получаем следующую формулу. 

(S = S_{бок.} + 2S_{осн.} = 2 pi RH+2 pi R^2 = 2 pi R(H + R))

Допустим, мы решили сделать чашку очень вкусного чая, но чтобы правильно его заварить нам нужно знать точный объем воды. Для этого вычислим объем цилиндра. Воспользуемся следующей формулой:

(V = S_{осн.}H = pi R^2H)

В этой формуле R — радиус цилиндра, Н — высота. 

Часто формулу объема можно применить для решения жизненных задач. Например, чтобы найти объем детали, погруженной в воду. 

Пример 1. В цилиндрическом сосуде налито 1650 см³ жидкости. В этот сосуд опустили деталь. При этом уровень жидкости увеличился в 1,2 раза. Найдите объем детали. Ответ выразите в см³. 

Решение. 

Шаг 1. Выразим высоту жидкости в первый и второй раз. Пусть вначале уровень жидкости был равен х, значит после того, как в нее опустили деталь, он стал равен 1,2х. 

Шаг 2. Вспомним физику и заметим, что объем жидкости в сосуде после того, как в него опустили деталь, будет равен сумме объемов жидкости и детали: V = V_ж + V_д. 

Шаг 3. С помощью объема жидкости выразим площадь основания сосуда:

V_ж = S_осн.H
1650 = S_осн.x
(S_{осн} = frac{1650}{x})

Шаг 4. Подставим площадь основания в формулу объема жидкости после того, как в нее опустили деталь:

(V = S_{осн.}H = frac{1650}{x} * 1,2x = 1980)

Шаг 5. Тогда объем детали будет равен:

V_д = V — V_ж
V_д = 1980 — 1650 =330 

Ответ: 330 см³

Фактчек

• Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. Цилиндр может быть прямым и наклонным. В наклонном цилиндре ось не перпендикулярна основаниям цилиндра. 
• Цилиндр состоит из двух оснований и цилиндрической поверхности (боковой поверхности цилиндра). Основания имеют форму кругов, равны между собой и лежат в параллельных плоскостях. Развертка боковой поверхности имеет форму прямоугольника. 
• Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. В прямом цилиндре образующая равна высоте цилиндра. Образующие равны и параллельны друг другу, а также образуют боковую поверхность цилиндра. 
• Осевое сечение цилиндра проходит через его ось и является прямоугольником. Любое сечение, параллельное осевому, также будет являться прямоугольником. Перпендикулярное сечение проходит перпендикулярно оси цилиндра и параллельно его основаниям. Перпендикулярное сечение имеет форму круга. 

Проверь себя

Задание 1. 
Что такое образующая цилиндра?

1. Ось вращения, с помощью которой получен цилиндр.
2. Диаметр оснований цилиндра.
3. Любой перпендикуляр, проведенный от одного основания к другому.
4. Отрезок, соединяющий точки окружности основания. 

Задание 2. 
Площадь боковой поверхности цилиндра равняется 44. Его радиус равен 8. Найдите высоту цилиндра. 

1. 2,75
2. 5,5
3. (2,75 pi)
4. 2

Задание 3. 
Площадь основания цилиндра равна 16. Его высота равна 4. Найдите площадь полной поверхности цилиндра. 

1. 64
2. (64 pi)
3. 32
4. (32 pi)

Задание 4. 
Объем цилиндра равен 28, а его высота равняется 7. Найдите диаметр основания.

1. 4
2. 2
3. 16
4. 8

Ответы: 1. – 4 2. – 1 3. – 2  4. – 1

Сечение цилиндра: определение, виды, его образующая

Содержание:

• Кратко о цилиндре
• Осевое сечение
• Как найти площадь сечения
• Осевое сечение наклонного цилиндра
• Примеры задач
  • Задача 1
  • Задача 2

Кратко о цилиндре

Цилиндр — это геометрическая фигура, которая ограничена цилиндрической поверхностью и двумя плоскими окружностями.

Также можно сказать, что это тело вращения, возникающее при вращении прямоугольника вокруг его стороны.

Осевое сечение

Это сечение фигуры плоскостью, проходящей через ее ось. Оно является прямоугольником. Таким образом, любое сечение, параллельное оси цилиндра (и перпендикулярное его основанию), становится прямоугольником. Сторонами этой фигуры будет диаметр цилиндра и высота его оси.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как найти площадь сечения

Формула 1

(S = d*h,)

где (d) — диаметр, а (h) — высота всей фигуры.

Также есть формулы для расчета площади сечения, параллельного оси геометрического тела (но не пересекающего ее).

Формула 2

(S = a*h, )

где (a) — хорда.

Осевое сечение наклонного цилиндра

Сечение наклонного цилиндра по оси представляет собой параллелограмм. Его стороны нам уже известны: одна из них равна диаметру d, как и в случае с прямой фигурой. Другая — длина образующего отрезка. Ее мы можем обозначить буквой b.

Для точного определения всех параметров параллелограмма недостаточно знать только длины его сторон. Для расчета площади фигуры нам понадобится один из ее углов. Допустим, что острый угол между плоскостью и направляющий равен α. Тогда формула S параллелограмма будет выглядеть следующим образом:

(S = d * b * sin(α))

Примеры задач

Рассмотрим пару задач на осевое сечение с решениями.

Задача 1

Дан круглый прямой цилиндр. Его осевое сечение является квадратом. Вопрос: чему равна S сечения, если площадь поверхности всего цилиндра — 100 см²?

Решение

Чтобы найти S квадрата, нужно сначала определить радиус или диаметр окружности цилиндра. Для этого вспомним формулу для нахождения площади самого цилиндра:

(Sц = 2pi * r * (r + h))

Так как осевое сечение — квадрат, значит радиус основания в два раза меньше высоты фигуры. В таком случае, формула будет выглядеть так:

(Sц = 2pi * r * (r + 2r) = 6 * pi * r²)

Исходя из этого, будем выражать радиус:

(r = √(Sц / (6*pi)))

Если сторона квадратного сечения равна диаметру основания цилиндра, то для определения площади квадрата S используем формулу:

(S = (2*r)2 = 4*r2 = 2*Sц/ (3*pi))

Подставим известные данные ((Sц = 100см^2)) и получим площадь сечения (S = 21,23 см²).

Ответ: (S = 21,23 см²).

Задача 2

Дано: ABCD — осевое сечение цилиндра. Площадь сечения (Sc) равна (10 м²), а площадь основания (Sо— 5 м²). Найти высоту цилиндра.

Решение

Так как площадь основания — круг, то (Sо = pi * r²). Тогда (r = √(Sо/pi) = √(5/pi).)

Так как площадь сечения  — прямоугольник, то (Sc = AB * BC = h * 2r.) Тогда (h = Sc/(2r) = 10/(2√(5/pi)) = 5√(pi/5) = √(5pi).)

Ответ: (h = √(5pi).)

Текст с ошибкой:

Расскажите, что не так

Уравнение диаметра проходящего через точку

Глава 22. Диаметры линий второго порядка

В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением

(1)

то его диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

Если гипербола задана уравнением

, (2)

то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

Все диаметры параболы параллельны ее оси. Если парабола задана уравнением

,

то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.

Если k и k ’ – угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то

(3)

Если k и k ’ – угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то

(4).

Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.

Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.

Уравнение кривой второго порядка

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Диаметры кривой. Главные оси. Асимптоты. Уравнение кривой, отнесенной к сопряженным направлениям; уравнение кривой, отнесенной к асимптотам.

Если в кривой второго порядка провести все хорды одного и того же направления, то геометрическое место середин этих хорд представит некоторую прямую, которую называют диаметром, сопряженным данным хордам. Уравнение диаметра:

где есть угловой коэффициент сопряженных хорд. Меняя , т.е. меняя направление хорд, получим бесчисленное множество диаметров; все они проходят через центр кривой. У параболы все диаметры параллельны между собой.

Направление хорд и направление сопряженного им диаметра называются сопряженными направлениями относительно данной кривой. Зависимость между двумя сопряженными направлениями следующая:

Сопряженными диаметрами называются такие два диаметра, из которых каждый делит пополам хорды, параллельные другому. У параболы сопряженных диаметров нет, так как все диаметры имеют одно и тоже направление.

Главными осями кривой называются диаметры, перпендикулярные к сопряженным хордам; их направления называются главными направлениями.

В случае прямоугольной системы координат главные направления определяются из уравнения:

где – угол между одним из главных направлений и направлением оси .

В случае косоугольной системы координат имеем:

Всякая кривая второго порядка имеет два главных направления, за исключением окружности, для которой главные направления неопределенные.

Угловой коэффициент определяется для всех диаметров параболы по формуле:

если для старших коэффициентов параболы введены обозначения:

Главная ось параболы как один из ее диаметров имеет это же направление и в случае прямоугольных координат она изображается уравнением

Второе главное направление параболы перпендикулярно к ее диаметрам, но второй главной оси у параболы нет. Если отнести кривую у двум сопряженным направлениям, т.е. выбрать за оси координат прямые, имеющие сопряженные направления относительно этой кривой, то в уравнение кривой не войдет член с произведением координат (). У параболы кроме того, исчезнет ещё один из старших членов ().

Если центральную кривую отнести к двум сопряженным диаметрам (или к главным осям), то уравнение ее примет вид:

Простейшее уравнение параболы мы получим, поместив начало координат в вершину, т.е. в точку пересечения параболы с главной осью (), выбрав главную ось за ось абсцисс (, и ) и касательную в вершине (она перпендикулярна к оси) за ось ординат:

При таком же выборе осей координат центральная кривая изобразится уравнением

Асимптоты кривой можно рассматривать как те ее диаметры, которые сами себе сопряжены. Угловые коэффициенты асимптот определяются из уравнения

Асимптоты могут быть только у центральных кривых: гипербола имеет две действительные асимптоты, эллипс – две мнимые; в случае пересекающихся прямых асимптоты совпадают с этими прямыми.

Если принять асимптоты гиперболы за оси координат, то уравнение этой гиперболы примет вид:

587. Найти два сопряженных диаметра кривой , из которых один проходит через начало координат.

Решение . Данная кривая центральная, потому что . Уравнение всякого ее диаметра будет где – угловой коэффициент сопряженного диаметра. Так как искомый диаметр проходит через начало координат, то свободный член его уравнения должен равняться нулю, т.е. откуда . Вставив это значение параметра в общее уравнение диаметра и преобразовав его, получим: . Это уравнение одного из искомых диаметров; его угловой коэффициент ; следовательно, уравнение сопряженного диаметра будет:

588. Через точку (1;-2) проведен диаметр кривой . Найти уравнение этого диаметра и диаметра ему сопряженного.

589. Дана кривая . Найти ее диаметр, параллельный оси абсцисс, и диаметр, ему сопряженный.

590. Найти два сопряженных диаметра кривой , из которых один параллелен оси ординат.

591. Дана кривая и один из ее диаметров . Найти диаметр, ему сопряженный.

592. Составить уравнение диаметра кривой , параллельного прямой .

593. Определить диаметр кривой , образующий угол в с осью абсцисс. Угол .

594. Дана кривая: . Найти геометрическое место середин ее хорд: 1) параллельных оси ; 2) параллельных оси ; 3) параллельных прямой .

595. Найти диаметр кривой , проходжящей через середину хорды, отсекаемой этой кривой на прямой .

596. Найти середину хорды, отсекаемой кривой на прямой .

597. Найти такие сопряженные диаметры кривой , которые образуют между собой угол в . Угол .

598. Найти зависимость между угловыми коэффициентами прямых, имеющих сопряженные направления относительно:

1) эллипса ; 2) гиперболы .

599. Через точку (1;-3) провести хорду эллипса , сопряженную диаметру .

600. Найти направления и длину двух сопряженных диаметров эллипса , из которых один проходит через точку (2;3).

601. Найти угол между двумя сопряженными диаметрами эллипса , из которых один образует угол в с большой осью.

602. Определить длину тех сопряженных диаметров эллипса , которые образуют между собой угол .

Указание . В этой задаче удобно воспользоваться теоремами Аполлония: и , где и – полуоси эллипса; и – сопряженные полудиаметры его; – угол между этими сопряженными диаметрами.

603. Даны размеры двух сопряженных диаметров эллипса и и угол между ними . Вычислить длину его осей.

604. Определить угол между двумя сопряженными диаметрами гиперболы , зная, что действительный из этих диаметров втрое больше действительной оси.

605. Найти уравнения двух сопряженных диаметров гиперболы , угол между которыми равняется .

606. Дана парабола: . Написать уравнение диаметра этой параболы:

1) проходящего через начало координат;

2) сопряженного хордам, параллельным оси ;

3) сопряженного хордам, параллельным оси ;

4) образующего угол с сопряженными хордами;

5) перпендикулярного к сопряженным хордам.

Во всех случаях угол

607. Найти диаметр параболы , сопряженный тем хордам, которые наклонены под углом в к оси параболы.

608. Написать уравнение диаметра параболы , сопряженного с прямой .

609. Найти главные оси кривых:

Во всех случаях угол

610. Каковы будут главные оси распавшейся центральной кривой?

611. Найти ось параболы .

Решение . Все диаметры данной параболы имеют угловой коэффициент . Ось параболы есть диаметр, сопряженный перпендикулярным хордам, т.е. хордам с угловым коэффициентом (система координат предполагается прямоугольной). Уравнение всякого диаметра этой параболы будет при мы получим уравнение оси: .

612. Найти ось симметрии и вершину каждой из следующих парабол:

Во всех случаях угол

Указание . Вершина параболы находится как точка пересечение параболы с ее осью.

613. Найти общий диаметр двух кривых:

614. Составить уравнение кривой второго порядка, проходящей через начало координат, если известны две пары сопряженных ее диаметров:

Решение . Угловые коэффициенты сопряженных диаметров удовлетворяют уравнению: . Угловые коэффициенты данных диаметров: и , , ; вставляя эти значения в указанное уравнение, получим:

Координаты центра искомой кривой мы можем определить, решая совместно уравнения двух диаметров: , . Эти координаты должны удовлетворять уравнениям: и которые данном случае перепишутся так: и ; вставим вместо : и вычисленные их значения и тогда получим: и . Кроме того, кривая проходит через начало координат; значит, , и уравнение кривой будет:

615. Две пары прямых:

служат сопряженными диаметрами кривой второго порядка. Составить уравнение этой кривой, зная, что она проходит через точку (1;1).

616. Выяснить особенности в выборе осей координат, если кривые даны следующими уравнениями:

617. Относительно некоторой прямоугольной системы координат кривая дана уравнением: . Преобразовать это уравнение, приняв за оси координат главные оси кривой.

618. Отнести к главным осям кривые, данные относительно прямоугольной системы координат уравнениями:

619. Уравнение кривой, отнесенной к двум сопряженным диаметрам, составляющим угол , имеет вид: . Найти уравнение той же кривой относительно ее главных осей.

620. Отнести к главным осям кривые:

621. Выяснить особенности в выборе осей координат, если параболы даны следующими уравнениями:

622. привести к простейшему виду уравнение параболы ; .

623. Привести к простейшему виду уравнения следующих парабол:

624. Отнести к вершине следующие центральные кривые:

Во всех случаях .

625. Найти асимптоты следующих гипербол:

626. Доказать, что все кривые, уравнения которых отличаются друг от друга только свободными членами, имеют общие асимптоты. Найти, например, асимптоты кривых при различных значениях параметра λ.

627. Доказать, что если две кривые имеют общие асимптоты, то все члены их уравнений, кроме свободных членов, имеют пропорциональные коэффициенты.

628. Составить общее уравнение для всех кривых. Имеющих прямые и своими асимптотами.

629. кривая второго порядка проходит через точку (1;-1) и имеет своими асимптотами две прямые: и . Составить уравнение этой кривой.

630. Составить уравнение кривой, касающейся прямой и имеющей прямые и своими асимптотами.

630*. Какому условию удовлетворяют коэффициенты общего уравнения гиперболы, если гипербола равносторонняя?

631. Какой вид имеет уравнение гиперболы, если одна из осей координат или обе оси параллельны асимптотам?

632. Составить уравнение гиперболы, проходящей через точки (2;1), (-1;-2) и (), при условии, что одна из ее асимптот совпадает с осью абсцисс.

633. Уравнение гиперболы, отнесенной к главным осям, имеет вид: . Преобразовать это уравнение, приняв асимптоты гиперболы за новые оси координат.

634. Отнести гиперболу к ее асимптотам.

635. Как преобразуется уравнение гиперболы , если за оси координат принять ее асимптоты? Угол .

636. Сколько членов второй степени и какие именно могут войти в уравнение: 1) эллипса4 2) гиперболы; 3) параболы?

Преобразование уравнения кривой второго порядка с помощью инвариантов.

Если одна и та же кривая второго порядка, отнесенная к двум различным произвольно выбранным системам координат с координатными углами и , изображается уравнениями:

то имеют место следующие равенства:

т.е. существуют выражения, составленные из коэффициентов уравнения кривой и соответствующего координатного угла, которые не меняют своей величины ни при каком преобразовании декартовых координат. Такие выражения называются инвариантами кривой второго порядка. Мы можем пользоваться тремя вышеприведенными инвариантами:

для упрощения уравнений кривой второго порядка, если только уравнение кривой после преобразования содержит не более трех коэффициентов.

637. Пользуясь инвариантами, отнести к главным осям кривую , зная что .

Решение . Искомое уравнение имеет следующий вид:

Для прямоугольных систем координат инварианты упрощаются, так как и , и мы будем иметь: ; . Найдем числовое значение этих инвариантов, исходя из данного уравнения:

Составим теперь выражения этих же инвариантов через коэффициенты преобразованного уравнения: . Так как инварианты не меняют своей величины при преобразовании координат, то мы можем приравнять между собой найденные для них выражения, содержащие коэффициенты первоначального и преобразованного уравнения;. Из этой системы уравнений мы определяем неизвестные коэффициенты преобразованного уравнения: ;, и искомое уравнение будет . Таким образом, пользуясь инвариантами, можно привести уравнение кривой к простейшему виду, не отыскивая ее центра, осей и не составляя формул преобразования координат.

638. Пользуясь инвариантами, привести к простейшему виду уравнения следующих кривых:

при условии, что все они отнесены к прямоугольной системе координат.

639. Пользуясь инвариантами, упростить уравнения следующих кривых:

Во всех случаях .

640. Упростить уравнения следующих кривых:

640*. Отнести к главным осям кривую , если известно, что .

641. Отнести гиперболу к ее асимптотам, пользуясь инвариантами. Угол .

Решение . Уравнение кривой, отнесенной к асимптотам, имеет вид:

Нам надо найти два неизвестных коэффициента , и новый координатный угол , т.е. угол между асимптотами. Найдем числовую величину инвариантов, пользуясь данным уравнением, при , : . Выражения этих инвариантов в новых коэффициентах будут:

Для определения трех величин , и имеем три уравнения:

Решив их, получим: , ; и ; искомое уравнение будет: . Выбираем направление осей так, чтобы гипербола была расположена в нормальном угле и вертикальном к нему угле; тогда после упрощений получим: .

642. Отнести к асимптотам гиперболы, данные относительно прямоугольной системы координат уравнениями:

643. Относительно некоторой прямоугольной системы координат кривая изображается уравнением . Составить уравнение этой же кривой относительно ее вершины.

Указание . Отнести кривую к вершине – значит принять одну из осей кривой за ось абсцисс, перенести начало координат в вершину и принять касательную в вершине за ось ординат.

[spoiler title=”источники:”]

http://infourok.ru/uravnenie-krivoy-vtorogo-poryadka-2812642.html

[/spoiler]

Зубчатые
колеса, шкивы, звездочки и другие
вращающиеся детали машин устанавливают
на валах или осях.

Вал
– деталь машин, предназначенная для
поддержания сидящих на нем деталей и
передачи крутящего момента. При работе
вал испытывает деформации кручения и
изгиба, иногда – растяжения-сжатия.

Ось
– деталь машин и механизмов, служащая
для поддержания вращающихся частей,
но не передающая полезный крутящий
момент, а, следовательно, не испытывает
кручения.

Классификация
валов и осей

Виды
валов:

1)
коренные,

2)
шпиндели,

3)трансмиссионные.

По
форме геометрической оси валы бывают:

1)
прямые, 2) коленчатые; 3)гибкие.

По
типу сечения валы бывают:

1)
сплошные; 2) полые.

Оси
бывают вращающиеся и неподвижные.

Прямые
валы и оси изготавливают гладкими или
ступенчатыми. Образование ступеней
связано с различной напряженностью
отдельных сечений, а также с условиями
изготовления и сборки.

Рис.
3.44. Опорные части вала и оси

Отличие:

Возьмем
для примера тяжелый железнодорожный
вагон. Он установлен на 2 ходовые тележки;
8 пар колес этих тележек свободно катятся
по стальным рельсам. Толстые, прочные
оси, на которых закреплены колеса,
служат им только опорой и не передают
от одного колеса другому никаких усилий.
При этом ось может вращаться вместе с
колесами, как у вагона, а может быть
закреплена неподвижно, как у велосипеда.
Ось, как правило, имеет опоры с обоих
концов. Если же ось закреплена только
с одного конца, а на другом установлено
колесо — ее называют полуосью. На таких
полуосях установлены передние колеса
автомобиля. Это позволяет автомобилю
делать крутые повороты. У валов
«обязанности» значительно сложнее:
они не только поддерживают вращающиеся
детали, а, самое главное, передают
вращающие усилия от одной части механизма
другой.

Определение
диаметра вала (ориентировочно) по
формуле

d = A 3?(N/n) см

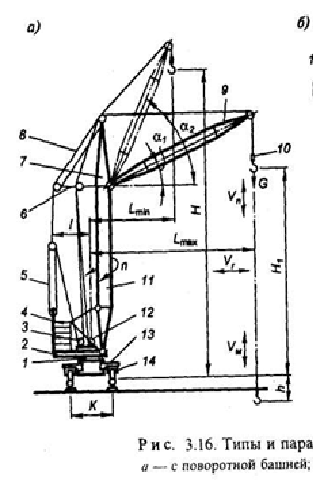
38.Башенный кран с поворотной башней.

«Башенные краны
с поворотной платформой: конструктивные
схемы, порядок монтажа-демонтажа,
параметры, преимущества и недостатки
по сравнению с другими схемами, область
применения. Правила безопасной
эксплуатации»

У кранов с поворотной
башней
опорно-поворотное
устройство 1,
на которое
опирается поворотная часть крана,
распо­ложено внизу на ходовой раме
крана или на портале. Поворотная часть
кранов включает (за исключением кранов
8-й размерной груп­пы) поворотную
платформу 2,
на которой
размещены грузовая 12
и стреловая
3 лебедки,
механизм поворота, противовес 4,
башня 11
с оголовком
7, распоркой 6
и стрелой
9.

Монтаж и демонтаж
кранов осуществляются собственными
ме­ханизмами и стреловым самоходным
краном грузоподъемностью 25 т. Для
подъема и опускания верхней части крана
при монтаже и демонтаже секций башни
служит монтажная стойка, состоящая из
собственно стойки, лебедки, площадок,
обойм полиспаста, блока и катушки. При
монтаже или демонтаже стойка крепится
на секциях башни в специальных
кронштейнах. Стойка состоит их трехгранной
фермы, имеющей внизу портал, в котором
располагается монтаж­ная лебедка.

Все башенные краны
оборудуются приборами безопасности.
К ним относятся ограничители крайних
положений всех видов дви­жения,
расположенные перед упорами: передвижения
крана, грузо­вой и контргрузовой
тележек, угла наклона стрелы, поворота,
высо­ты подъема, выдвижения башни и
т. д. Для защиты кранов от перегрузки
при подъеме груза на определенных
вылетах применяют ограничители
грузоподъемности. Краны также оснащают
тормоза­ми на всех механизмах рабочих
движений, нулевой и концевой
элек­трозащитой, аварийными кнопками
и рубильниками, анемометра­ми с
автоматическим определением опасных
порывов ветра и подачей звуковых и
световых сигналов для предупреждения
маши­ниста об опасности, рельсовыми
захватами на ходовых тележках, указателями
вылета крюка и грузоподъемности на
данном вылете при соответствующей
высоте подъема груза и т. п. Для прохода
ма­шиниста в кабину и к удаленным
узлам для проведения техническо­го
обслуживания и ремонта на кранах
устанавливают лестницы, площадки и
настилы, имеющие необходимое ограждение.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Типоразмеры колес и шин к садовым тачкам

Существует несколько методов обозначить размер и параметры шины, некоторые производители используют размеры в дюймах, некоторые в миллиметрах, а некоторые – даже в обеих величинах. Примеры, приведенные ниже, помогут Вам определить параметры самостоятельно.

1. Ширина шины (ширина поперечного сечения)
2. Высота шины
3. Высота в поперечном сечении
4. Диаметр обода
5. Наружный диаметр шины

Пример: 3.00-4, 3.50-6, 4.00-8, 5.20-10, 6.00-12…. Первая цифра (3.00) обозначает ширину шины. “-” — обозначает то, что шина является диагональной (радиальная конструкция была бы обозначена буквой R). Последняя цифра (4) обозначает посадочный диаметр в дюймах. Таким образом, шина с параметрами 3.00-4 подходит для 4 дюймового диска, имеет ширину в 3 дюйма и диагональную конструкцию.

Пример: 6-12, 7-14, 8-16, 9.5-18…

То же самое, что и в предыдущем пункте, но без (.00) в первой части типоразмера. Все размеры в дюймах. Важно, что шины с похожими типоразмерами могут не быть совместимыми – шина с параметрами 6.00-12 может очень значительно отличаться от шины 6-12. Если Вы сомневаетесь в определении совместимости – обратитесь к менеджерам Промтехники.

Пример: 4.10/3.50-4, 4.10/3.50-6, 5.30/4.50-6…

Этот типоразмер состоит из 4х частей. Первая цифра (4.10) обозначает ширину шины. Вторая (3.50) обозначает высоту шины. Третья цифра (4) обозначает посадочный диаметр шины. “-” говорит о диагональной конструкции шины. Таким образом, шина с типоразмером 4.10/3.50-4 имеет ширину 4.1 дюйма, высоту 3.5 дюйма, подходит для дисков диаметром 4 дюйма и имеет диагональную конструкцию.

Пример: 11х4.00-4, 13х5.00-6, 18х8.50-8, 25х12.00-9…

Первая цифра (11) – это внешний диаметр шины в дюймах. Вторая цифра (4.00) – это ширина шины в дюймах, и третья цифра (4) обозначает посадочный диаметр шины. “-” говорит о диагональной конструкции шины. Таким образом, шина с типоразмером 11х4.00-4 имеет внешний диаметр 11 дюймов, ширину – 4 дюйма, подойдет для диска диаметром 4 дюйма и имеет диагональную конструкцию.

Пример: 10х3, 18х4, 260х85

Такая маркировка является устаревшей, но Вы всё ещё можете с ней столкнуться. Размеры могут указываться как в дюймах, так и в миллиметрах (обычно различить это достаточно легко). Первая цифра (10) обозначает внешний диаметр шины, вторая – ширину шины. Посадочный диаметр не обозначен в типоразмере, но может быть легко вычислен, так как высота такой шины обычно совпадает с ее шириной. Таким образом, шина с типоразмером 18х4 имеет внешний диаметр 18 дюймов, ширину 4 дюйма и посадочный диаметр в 10 дюймов (18 дюймов внешнего диаметра минус 2х4” высоты шины). Современным обозначением для такой шины была бы формула 4.00-10. Шина с типоразмером 260х85 имеет внешний диаметр 260мм и ширину 85мм, или 10” и 3” соответственно, посадочный диаметр – 4 дюйма. Современное обозначение выглядело бы так: 3.00-4.

Пример: 255/60-10, 195/50R13, 420/85R28

Первая цифра – это ширина шины в миллиметрах, вторая – высота профиля (процент от ширины шины), третья цифра – посадочный диаметр в дюймах. Если в типоразмере присутствует буква R – это означает, что шина имеет радиальную конструкцию, а “-” обозначает диагональную. Таким образом, шина с типоразмером 420/85R28 имеет ширину 420мм, профиль – 85% (высота шины равно 85% от ширины, то есть 357мм), радиальную конструкцию и подходит к диску диаметром 28 дюймов.

Пример: 145R10, 155R12

Первая цифра обозначает ширину шины в миллиметрах, а вторая – посадочный диаметр (диаметр диска) в дюймах. R указывает на радиальную конструкцию, “-” – на диагональную. При такой маркировке профиль шины не указывается, и по умолчанию равен 80%. То есть шина с типоразмером 145R10 имеет ширину 145мм, высоту 116мм (80% от 145мм), подходит для диска диаметром 10 дюймов и имеет радиальную конструкцию. Общий диаметр шины можно высчитать переведя все единицы измерения в дюймы или миллиметры и сложив диаметр диска с двойной величиной высоты шины.

В настоящее время норма слойности определяет прочность шины и не указывает количество слоев кордной ткани. Первоначально термин «слой» действительно относился к числу слоев кордной ткани и поэтому служил показателем прочности шины. Но с развитием новых материалов исходную хлопковую кордную ткань сначала заменили на вискозу, а в настоящее время используют нейлон или стальную проволоку.

В результате появилась возможность значительно повысить прочность без увеличения числа слоев материала. Поэтому термин «количество слоев кордной ткани» стал использоваться скорее для обозначения прочности шины, а не для указания действительного числа слоев.

Звездочки (*,**,***) используются для обозначения прочности радиальных шин.

Источник

Характеристики колёс для тележки или тачки

Существует много видов колёс для тележек, в зависимости от самих тележек:

• Грузовые тележки. На этот вид тележек монтируются обычно два вида колёс: колёса на литовой резине (используются часто в строительстве, где высокий риск прокола камеры) и пневматические колёса (чаще используются при перемещении по ровной поверхности)

• Гидравлические. Здесь стоит различать между рулевыми колёсами и подвилочными роликами. Ролики изготавливаются из таких материалов, как полиамид или полиуретан. Можно крепить по одному или парой. Рулевые колёса состоят из алюминия или чугуна.

• Платформенные тележки. Здесь важно учесть, где эти колёса будут ездить, по каким поверхностям и что они будут перевозить. Важно выбирать поворотные или фиксированные колёса.

Характеристики колёс для тележки или тачки:

1. Внешний диаметр колеса – это первый и самый важный параметр при выборе колеса для хозяйственной тележки. Он определяется достаточно просто, рулеткой (есть диаметром 260 мм, 360 мм, 310 мм и тд.)
2. Диаметр оси колеса – необходимо замерить внутренний диаметр на колесе отверствия посередине либо диаметр оси. Самые распространенные диаметры осей считаются 16, 20 и 25 мм.
3. Тип ступицы. Ступицы бывают:

• Симметричные (одинаковые с двух сторон)
• Не симметричные (каждая её сторона отличается)

1. Ширина ступицы колеса – тоже очень важный параметр. Характеризуется вылетом оси на вашей тележке. Если вдруг ширина ступицы колеса, например, оказалась больше, чем вылет оси, то колесо вы не сможете зафиксировать на тележке.
2. Материал ступицы колеса. Бывает колесо:

• С пластиковой ступицей
• С металлической ступицей

По качеству оба вида колёс примерно одинаковой износостойкости.

Подбор колес для тележек – это очень ответственное задание, потому что от него может зависеть скорость работ, их легкость, и, что самое главное, безопасность. Учитывая все факторы и критерии, зная свойства различных материалов и особенности способов крепления, вы можете выбрать именно те колеса, которые идеально подойдут для вашей тележки и позволят вам перевозить грузы максимально комфортно.

Источник

Как подобрать колесо для тачки?

Тележки для сада или строительства должны быть удобными в использовании и безопасными. Периодически они требуют замены колёс для сохранения работоспособности. От их вида и размеров зависит грузоподъёмность и прочность тележки. Правильно выбрать колесо для тачки поможет знание его параметров и разновидностей.

Колёса для тачек изготавливаются из разных материалов, в зависимости от будущего назначения. Для садовых тележек, например, не нужны детали, обладающие высокой грузоподъёмностью.

Именно от неё и отталкиваются покупатели. Колёса для тачек бывают:

Подкачиваемые колёса. От давления в них зависит грузоподъёмность тачки.

Не имеют камеры, поэтому отличаются жёстким ходом. Но тачки с такими колёсами защищены от проколов.

Пневматические колёса подходят для работ в саду. Они с лёгкостью преодолевают невысокие препятствия, не требуют особого ухода и плавны в движении.

Полиуретановые колёса защищены от проколов, следовательно, отлично подойдут для стройплощадок с мусором. Они имеют долгий срок службы и плавный ход. Полиуретан защищён от воздействия слабоагрессивных веществ, находящихся в температуре от -30 до +50°С.

Размеры и обозначения

Диаметр колеса тачки напрямую влияет на его проходимость. Чем он больше, тем легче будет управляемость тележкой.

Размеры обозначаются на покрышках. Измеряются они в миллиметрах и дюймах. В обозначениях указываются следующие параметры:

1. Ширина и высота поперечного сечения.
2. Наружный диаметр.
3. Диаметр оси крепления.

Например, обозначение 3,25/3.00-8 D16 расшифровывается как:

• 3,25 дюйма – ширина покрышки.
• 3,00 дюйма – высота покрышки.
• 8 дюймов – диаметр посадки.
• 16мм – диаметр оси

При покупке колеса важно учитывать ограничение по диаметру. Для садовых условий нужна манёвренная тачка, а для стройплощадки – прочная и грузоподъёмная. Пневматические колёса дешёвые, но требуют постоянной подкачки. Полиуретановые, напротив, стоят дороже, но отличаются высокой надёжностью и устойчивостью к деформациям.

Источник

Как выбрать колесо для садовой тачки

Садовый и строительный инструмент обязан быть надёжным, чтобы не подводил в ответственный момент, когда на участке огромное количество работы. Садовая тачка периодически нуждается в замене колёс, от грамотности выбора которых зависит грузоподъёмность прибора, а также его срок службы.

Как подобрать колесо для садовой тачки?

Как и для автомобиля, колёса для тачки имеют большое значение. Они изготавливаются из разных материалов, бывают камерные и бескамерные. От их качества зависит грузоподъёмность прибора. Правильно выбранные комплектующие помогают беспрепятственно перевозить по участку запланированные грузы.

Рассчитывать нагрузку необходимо на каждую сторону отдельно.

Виды колёс

Чаще всего современные инструменты комплектуются полиуретановыми бескамерными колёсами. Они не боятся слабоагрессивных сред, не деформируются при контакте с различными маслами и бензином, выдерживают температурный разброс от +50 до -30 градусов. Крайне просты в обслуживании — требуется только очищать грязь. Жёсткие в ходу, но при этом не боятся проколов.

Пневматические предпочтительнее для садовой тачки, так как способны преодолевать небольшие препятствия в виде кирпичей и бордюра. Боятся проколов. От давления в шине зависит жёсткость хода, а также грузоподъёмность прибора.

Размеры колёс

Размерная сетка комплектующих обширная — зависит от размера корыта и грузоподъёмности тачки. Маркировка производится тремя значениями:

1. Ширина комплектующей.
2. Высота шины.
3. Диаметр диска.

Обычно рекомендуемая окружность промаркирована в инструкции производителя. В крайнем случае можно взять старое колесо и отправится с ним в магазин, где консультанты подберут подходящее.

Важно знать диаметр оси, на которую крепят запчасть. Чаще всего встречаются значения в 16 и 20 мм.

Приведём пример. На этикетке указана маркировка 3,25/3,00-8 D16. Здесь 3,25 — это ширина шины, 3,00 — высота, 8 — диаметр диска, а D16 — окружность оси. Отступать от этих значений не рекомендуется из-за повышения нагрузки на устройство.

Как правильно выбрать?

Чтобы купить комплектующие, обращаем внимание на несколько параметров:

• Диаметр. Самыми распространёнными показателями считаются 250, 350 и 400 мм.
• Внутренняя окружность диска. Здесь чаще встречаются 16 и 20 мм.
• Определиться с наличием камеры или её отсутствием, с материалом, из которого оно изготовлено.
• Понять, необходимо симметричное колесо или нет.

Зная ответы на поставленные вопросы, прочитав информацию от производителя тачки с рекомендациями, вам удастся сделать верный выбор в магазине.

Источник