Найди верный ответ на вопрос ✅ «Как найти диаметр основания конуса*помогите если длинна оброзующей 37 высота конуса = 12 …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Алгебра » Как найти диаметр основания конуса*помогите если длинна оброзующей 37 высота конуса = 12
Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.
Круглый прямой конус
В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая – директрисой, или направляющей.
Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.
Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.
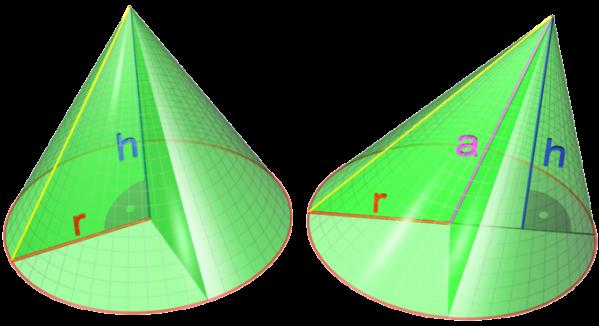
Здесь r – радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.
Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая – это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.
Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.
Вычисление диаметра фигуры через линейные параметры и угол при основании
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.
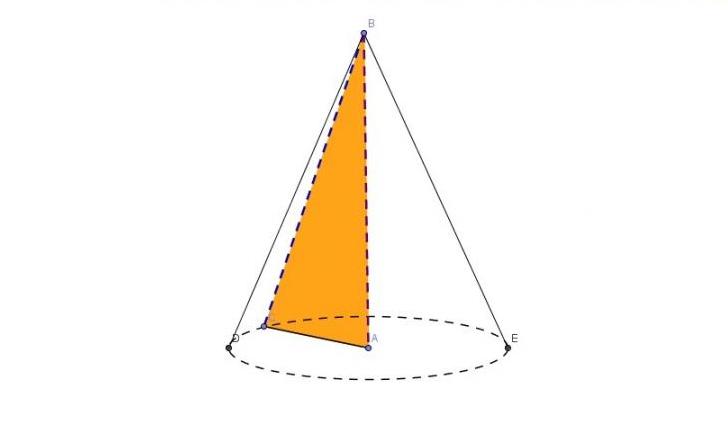
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g – это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
d = 2*√(g2 – h2)
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
d = 2*g*cos(φ);
d = 2*h/tg(φ)
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Вычисление диаметра через площадь поверхности и генератрису
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.
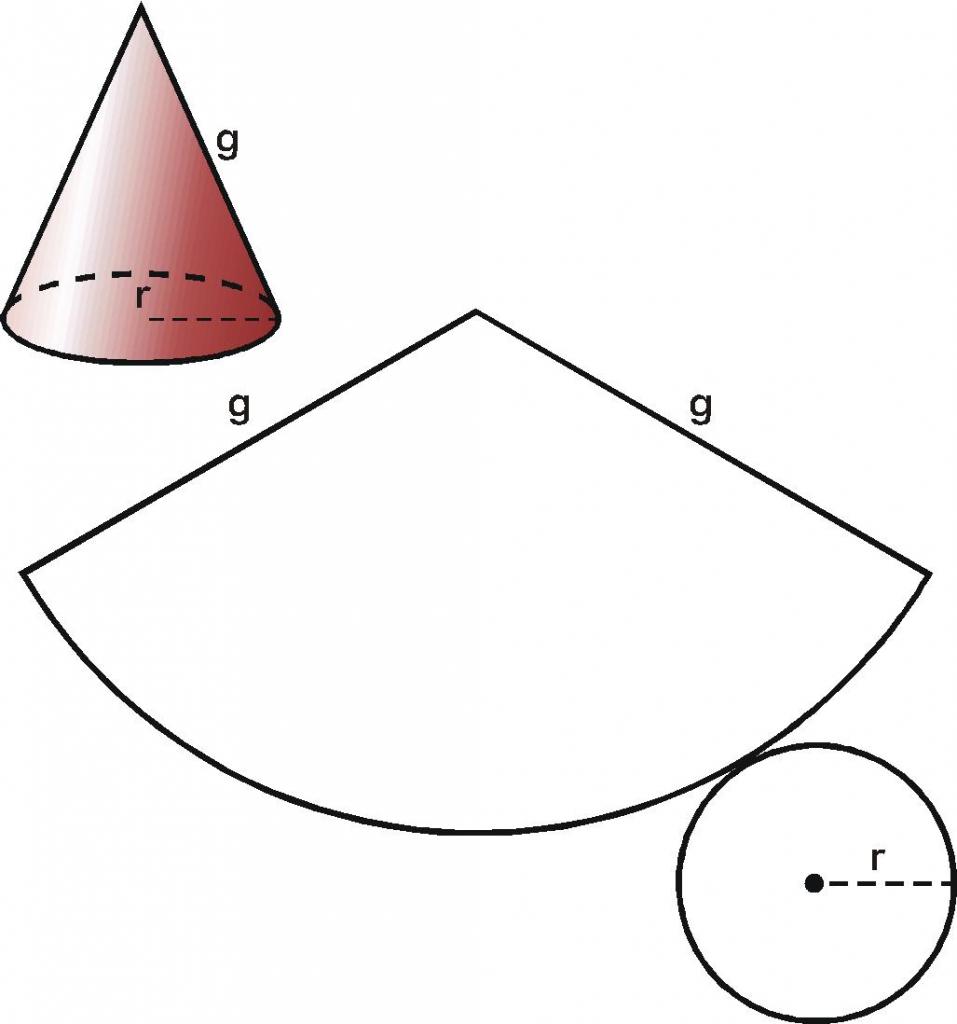
Общая площадь развертки определяется по следующей формуле:
S = pi*r2 + pi*r*g
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Определение диаметра через объем и высоту

Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
V = 1/3*S*h
Здесь S – площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
V = 1/3*pi*r2*h
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
r = √(3*V/(pi*h));
d = 2*r = 2*√(3*V/(pi*h))
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Задача на определение диаметра через известную площадь конуса и его образующую
Дан конус, площадь поверхности которого составляет 150 см2. Генератриса равна 14 см. Чему равен диаметр конуса?
Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:
S = pi*r2 + pi*r*g =>
r2 + 14*r – 150/3,14 = 0
При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:
D = 142 – 4*1*(-150/3,14) = 387,0828
Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:
r = (-14±√D)/2
Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:
r = (-14+√387,0828)/2 = 2,837 см
Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.
В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.
Знаток
(264),
закрыт
10 лет назад
Екатерина
Мастер
(1565)
10 лет назад
Высота конуса, его образующая и радиус образуют прямоугольный треугольник, в котором гипотенуза – образующая (длина 13), первый катет – высота конуса (длина 12), второй катет – половина искомого диаметра конуса.
По теореме Пифагора находим половину диаметра конуса:
х^2=13^2-12^2
x^2=25
x=5
Тогда диаметр конуса равен 2*х=10.
Loky
Мастер
(1744)
10 лет назад
образующая, высота и радиус = прямоугольный треугольник. Находишь катет 13 в квадрате- 12 в квадрате и из разницы корень – итого 5. Диаметр 10. Учи геометрию, пригодится.
Конусом (прямым круговым конусом) называется тело, состоящее из круга (основания конуса), точки, не лежащей в плоскости этого круга (вершины конуса), и всех отрезков, соединяющих вершину конуса с точками основания.
Конус является телом вращения.
Конус
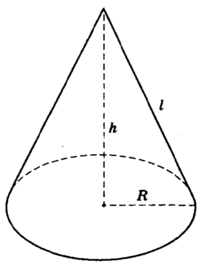
Рис.1
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Конус — тело, которое ограничено конической поверхностью и плоскостью, на которой лежат концы образующих конической поверхности.
Коническая поверхность — поверхность, которая образуется движением отрезка, один из концов которого неподвижен, а другой перемещается на плоскости вдоль некоторой кривой. Отрезки называют образующими конической поверхности, а кривую – направляющей. Неподвижная точка – вершина конической поверхности.
Боковая поверхность конуса — часть конической поверхности, ограниченная плоскостью.
Основание конуса — часть плоскости, отсекаемая боковой поверхностью конуса.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (См.Рис.1). В противном случае, конус называется наклонным. В школьном курсе изучается прямой круговой конус.
Круговой конус — конус, у которого в основании круг.
Прямой круговой конус (просто конус) — круговой конус, у которого прямая, соединяющая вершину конуса с центром круга, лежащего в основании, перпендикулярна плоскости основания.
Ось конуса — прямая, проходящая через вершину конуса и центр основания конуса.
Высота конуса — отрезок оси конуса, соединяющий вершину конуса с центром основания.
Конус можно рассматривать как тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей его катет.
Образующие конуса совпадают с образующими конической поверхности.
Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса.
См.Рис.2.
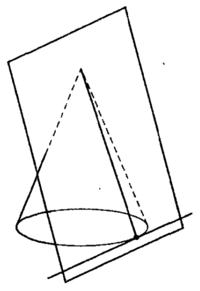
Рис.2
Развёртка боковой поверхности конуса — круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.
Площадь боковой поверхности (круглого) конуса равна произведению половины длины окружности основания (C) на образующую (l):
$$S_{бок}=frac{1}{2}cdot Cl=picdot rl$$
, где r – радиус основания, l – длина образующей.
Площадь полной поверхности конуса — сумма площадей основания конуса и его боковой поверхности, которая записывается формулой:
$$S_{полн}=picdot r(l+r)$$
, где r — радиус основания, l — длина образующей.
Объем всякого конуса равен трети произведения площади основания (S) на высоту (h):
$$V=frac{1}{3}cdot Sh$$
Объем круглого конуса:
$$V=frac{1}{3}cdot Sh=frac{1}{3}cdotpi r^2 cdot h$$
Усеченный конус – это часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания.
См.Рис.3.
Усечённый конус
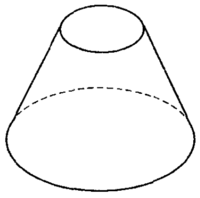
Рис.3
Формулы для усечённого конуса (См.Рис.4):
$$ S_{бок}=picdot lcdot (R+r)
\ S_{полн}=S_{бок}+pi(R^2+r^2)
\ V=frac{1}{3}picdot h(R^2+Rcdot r+r^2)
$$
Усечённый конус
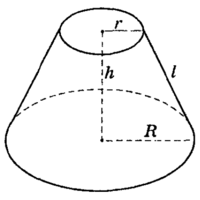
Рис.4

Пример 1. Высота конуса равна 4 , а длина образующей – 5. Найдите диаметр основания конуса.
Видео-решение.
Высота конуса равна 4 , а длина образующей – 5. Найдите диаметр основания конуса.

Высота конуса равна …
![]()
В этой статье рассмотрим задачи на нахождение элементов конуса. Конечно же, их можно отнести к одним из самых простых задач, которые входят в открытый банк заданий ЕГЭ по математике.
Как и многие задачи этой части, решаются они в одно-два действия. Несмотря на то, что это это стереометрическая задача, для решения достаточно знать теорему Пифагора. Рассмотрим задачи:

Высота конуса равна 57, а диаметр основания — 152. Найдите образующую конуса.
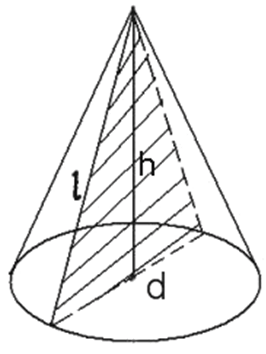
Рассмотрим осевое сечение конуса. По теореме Пифагора:

Ответ: 95
Как извлекать корень из большого числа читайте здесь.

Высота конуса равна 21, а длина образующей — 75 . Найдите диаметр основания конуса.

Диаметр основания конуса равен двум радиусам. Радиус мы можем найти по теореме Пифагора из прямоугольного треугольника:

Следовательно, диаметр основания конуса равен 144.
Ответ: 144

Диаметр основания конуса равен 56, а длина образующей — 100 . Найдите высоту конуса.

Рассмотрим осевое сечение конуса. По теореме Пифагора:

Ответ: 96
![]()
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Посмотреть решение
Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Посмотреть решение
Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
Посмотреть решение
В будущем рассмотрим и другие задачи с конусами, не пропустите. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия КОНУС ЦИЛИНДР | ЕГЭ-№2
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
