В этой задаче вам необходимо найти диаметр основания конуса, если известно что высота конуса равна 12, а длина образующей 15.
Построение рисунка к задаче
Важным этапом решения такого рода геометрических задач является построение рисунка. Для этого, прежде всего, необходимо определить форму конуса. В основании конуса может лежать круг, эллипс, гипербола и парабола. В задаче требуется найти диаметр основания конуса, поэтому мы будем считать, что в основании лежит именно круг.
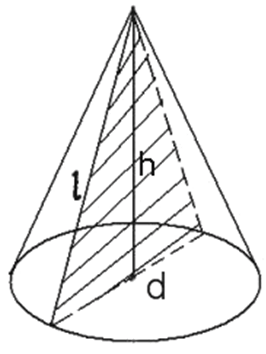
Построим рисунок и выделим на нем следующие элементы конуса:
- АВ – образующая конуса;
- АО – высота конуса;
- ВО – отрезок, соединяющий точки В и О.
http://bit.ly/2iFETTF
Заметим, что отрезок ВО также является радиусом круга, лежащего в основании конуса.
Анализ построения и нахождение диаметра основания
Рассмотрим изображенный на рисунке треугольник АВО. Так как АО высота конуса, то, по определению отрезок АО перпендикулярен плоскости основания конуса, а, значит,
∠АОВ = 90°.
Следовательно, по теореме Пифагора:
АВ^2 = АО^2 + ВО^2.
Таким образом, радиус основания конуса равен:
ВО = (АВ^2 – АО^2)^0,5 = (15^2 – 12^2)^0,5 = (225 – 144)^0,5 =
= 81^0,5 = 9.
Диаметр основания конуса равен удвоенному радиусу:
d = 2 * ВО = 2 * 9 = 18.
Ответ: диаметр основания конуса 18.
Найди верный ответ на вопрос ✅ «Как найти диаметр основания конуса*помогите если длинна оброзующей 37 высота конуса = 12 …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Алгебра » Как найти диаметр основания конуса*помогите если длинна оброзующей 37 высота конуса = 12
Через радиус конуса можно найти все параметры конуса, связанные с основанием, а значение высоты позволяет вычислить площади, объемы и все остальные объемные параметры конуса. Так, диаметр конуса равен удвоенному радиусу, периметр окружности в основании вычисляется по стандартной формуле через радиус, равно как и площадь основания.
d=2r
P=2πr
S_(осн.)=πr^2
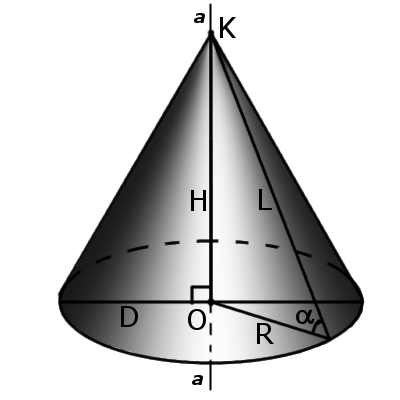
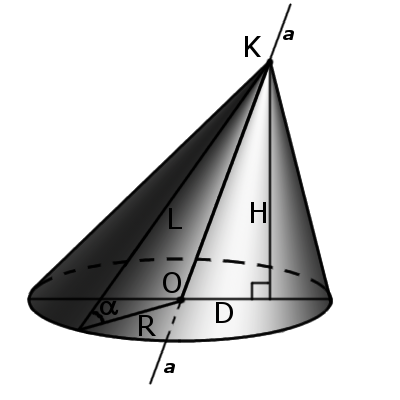
Прямоугольный треугольник, образованный высотой конуса, радиусом основания и образующей конуса, связывает эти три значения теоремой Пифагора, по которой можно вычислить неизвестную образующую, а также угол между образующей и основанием. Тем временем, угол α рассчитывается из равнобедренного треугольника, сформированного двумя образующими и диаметром из того принципа, что сумма всех углов в треугольнике равна 180 градусам. (рис.40.1, 40.2)
l=√(h^2+r^2 )
tanβ=h/r
α=180°-2β
Чтобы найти площадь боковой поверхности конуса, необходимо умножить радиус и апофему на число π. Площадь полной поверхности конуса состоит из площади его основания и площади боковой поверхности. В обеих формулах вместо апофемы нужно подставить квадратный корень через высоту и радиус, полученный по теореме Пифагора.
S_(б.п.)=πrl=πr√(h^2+r^2 )
S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)=πr(√(h^2+r^2 )+r)
Чтобы найти объем конуса, достаточно знать значения радиуса и высоты, тогда формула объема выглядит как произведение числа π на квадрат радиуса и высоту, деленное на три.
V=1/3 S_(осн.) h=(πr^2 h)/3
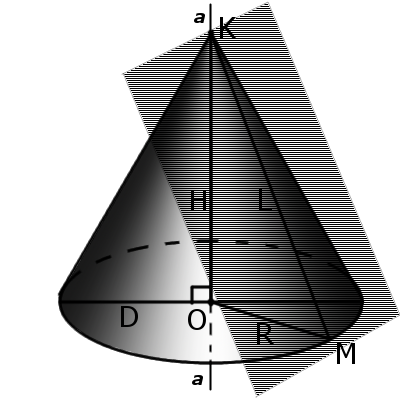
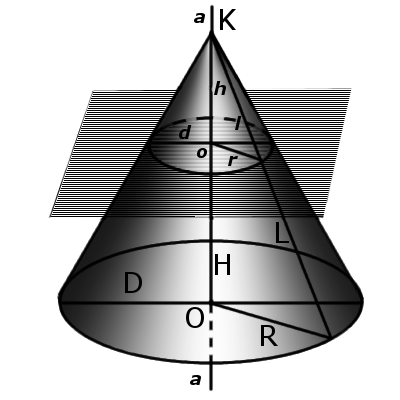
Радиус сферы, вписанной в конус, зависит не только от радиуса основания конуса и его высоты, но и от образующей, поэтому чтобы вычислить радиус вписанной сферы конуса через радиус конуса и высоту, нужно вместо образующей подставить полученное для нее выше выражение. Радиус описанной сферы может быть представлен сразу формулой только с переменными радиуса и высоты. (рис.40.3, 40.4)
r_1=hr/(l+r)=rh/(√(h^2+r^2 )+r)
R=(h^2+r^2)/2h
Высота конуса равна …
В этой статье рассмотрим задачи на нахождение элементов конуса. Конечно же, их можно отнести к одним из самых простых задач, которые входят в открытый банк заданий ЕГЭ по математике.
Как и многие задачи этой части, решаются они в одно-два действия. Несмотря на то, что это это стереометрическая задача, для решения достаточно знать теорему Пифагора. Рассмотрим задачи:
Высота конуса равна 57, а диаметр основания — 152. Найдите образующую конуса.
Рассмотрим осевое сечение конуса. По теореме Пифагора:
Ответ: 95
Как извлекать корень из большого числа читайте здесь.
Высота конуса равна 21, а длина образующей — 75 . Найдите диаметр основания конуса.
Диаметр основания конуса равен двум радиусам. Радиус мы можем найти по теореме Пифагора из прямоугольного треугольника:
Следовательно, диаметр основания конуса равен 144.
Ответ: 144
Диаметр основания конуса равен 56, а длина образующей — 100 . Найдите высоту конуса.
Рассмотрим осевое сечение конуса. По теореме Пифагора:
Ответ: 96
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Посмотреть решение
Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Посмотреть решение
Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
Посмотреть решение
В будущем рассмотрим и другие задачи с конусами, не пропустите. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия КОНУС ЦИЛИНДР | ЕГЭ-№2
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Элементы конуса
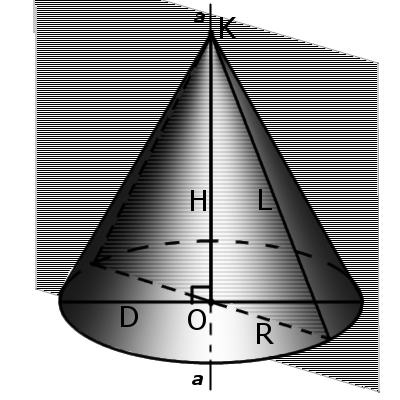
Определение. Вершина конуса – это точка (K), из которой исходят лучи.
Определение. Основание конуса – это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.
Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):
L2 = R2 + H2
Определение. Направляющая конуса – это кривая, которая описывает контур основания конуса.
Определение. Боковая поверхность конуса – это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.
Определение. Высота конуса (H) – это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
Определение. Ось конуса (a) – это прямая, проходящая через вершину конуса и центр основания конуса.
Определение. Конусность (С) конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса – это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:
где C – конусность, D – диаметр основания, d – диаметр меньшего основания и h – расстояние между основаниями.
Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:
где R – радиус основы, а H – высота конуса.
Определение. Осевое сечение конуса – это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника – это диаметр основания конуса.
Определение. Касательная плоскость к конусу – это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.
Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).
Определение. Прямой конус – это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Формула. Объём кругового конуса:
где R – радиус основы, а H – высота конуса.
Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:
Sb = πRL
Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:
Sp = πRL + πR2
Определение. Косой (наклонный) конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.
Формула. Объём любого конуса:
где S – площадь основы, а H – высота конуса.
Определение. Усеченный конус – это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.
Формула. Объём усеченного конуса:
где S1 и S2 – площади меньшей и большей основы соответственно, а H и h – расстояние от вершины конуса до центра нижней и верхней основы соответственно.
Уравнение конуса
1. Уравнение прямого кругового конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | – | z2 | = 0 |
| a2 | a2 | c2 |
2. Уравнение прямого эллиптического конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | = | z2 |
| a2 | b2 | c2 |
Основные свойства кругового конуса
1. Все образующие прямого кругового конуса равны между собой.
2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.
4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).
7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.